Dynamic response sensitivity of urban tunnel structures under blasting seismic waves to parameters
-
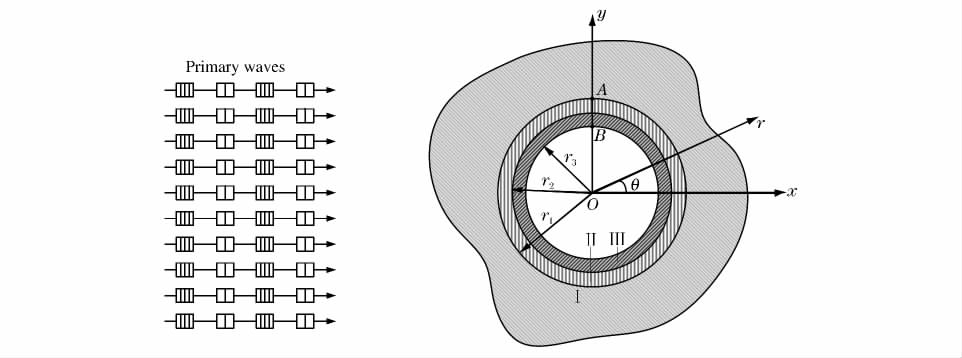
摘要: 选取纵波作为研究对象，采用波函数展开法，推导了无限弹性介质中复合衬砌结构隧道在爆破地震波作用下动力响应问题的解析解，结合南京红山南路隧道群开挖工程开展了隧道结构动应力集中因数的敏感性分析，并通过曲线拟合分别得到了隧道围岩及内衬环向动应力集中因数随隧道结构动力学及几何参数变化的回归方程。分析结果表明：隧道围岩和二次衬砌层的弹性模量及围岩泊松比对考察点处环向动应力的影响较大，而初期支护层弹性模量的影响几乎可以忽略不计；衬砌层厚度变化对围岩环向动应力的影响要远大于内衬，在隧道施工设计时可以通过增加衬砌层的厚度平衡隧道结构的受力状态，但增加初期支护层的效果不如二次衬砌层。Abstract: Primary waves were chosen as the study object, then an analytical solution for the dynamic response of tunnels with composite lining in infinite media under blasting seismic waves was deduced based on the wave function expansion method.According to the solution, the sensitivity of dynamic stress concentration factors to parameters was analyzed with the tunnel group excavation at Nanjing Hongshan South Road.By curve fitting, the regression equations were obtained for the hoop dynamic stress concentration factors of the surrounding rock and inner lining varied with the kinetic and geometrical parameters, respectively.The analysis result show that the elastic moduli of the surrounding rock and secondary lining and the Poisson's ratio of the surrounding rock have more impact on the hoop dynamic stress at the observation points and the effect of the elastic modulus of the primary lining is negligible.The lining thickness change has greater influence on the hoop dynamic stress of the surrounding rock than on the inner lining.Increasing the lining thickness can balance the stress states of the tunnel structures in designs and constructions, but the effect by the thicker inner lining is not as well as that by the thicker secondary lining.
-
图 1 爆破地震波衍射问题计算模型
Figure 1. Acalculation model for the diffraction problem of blasting seismic waves
图 2 实测爆破振动信号时程曲线及功率谱密度
Figure 2. Time history and power spectrum density of measurement signal
图 3 复合衬砌和单层衬砌条件下动应力集中因数对比
Figure 3. Comparison of dynamic stress concentration factors between composite－lining and single－lining tunnels
图 5 KA、KB随初期支护层弹性模量的变化
Figure 5. KAand KBvaried with elastic modulus of primary lining
图 6 KA、KB随二次衬砌层弹性模量的变化
Figure 6. KAand KBvaried with elastic modulus of secondary lining
表 1 敏感性分析所用的材料参数
Table 1. Materials parameters for sensitivity analysis
介质 E/GPa ρ/(g·cm-3) υ d/m 围岩(Ⅰ) 50(40~95) 2.60 0.26(0.20~0.40) C20砼(Ⅱ) 25(20~30) 2.50 0.25 0.15(0.10~0.30) C30砼(Ⅲ) 32(20~36) 2.50 0.30 0.45(0.25~0.60) 
下载: 导出CSV
表 2 动应力集中因数随隧道物理力学参数变化关系的回归方程
Table 2. Regression equations for relations between dynamic stress concentration factors and physico－mechanical parameters of tunnel
回归方程 R2 Srs KA=-0.230+0.019E1-1.818×10-4E12+6.608×10-7E13 0.999 2.996×10-4 KB=5.183-0.012E1+1.100×10-3E12-4.032×10-6E13 0.999 7.920×10-3 KA=0.345+2.512×10-4E2-2.697×10-5E22 0.978 3.875×10-4 KB=2.012-1.037×10-2E2+9.276×10-5E22 0.997 1.713×10-4 KA=0.601-8.320×10-3E3 0.999 3.171×10-4 KB=0.047+5.501×10-2E3 0.999 1.390×10-3 KA=0.479-1.763×10-2υ-2.075υ2 0.999 1.098×10-4 KB=2.221-0.743υ-3.213υ2 0.999 1.132×10-4
下载: 导出CSV
表 3 动应力集中因数随隧道几何尺寸变化关系的回归方程
Table 3. Regression equations for variations of dynamic stress concentration factors with geometrical dimensions of tunnel
回归方程 R2 Srs KA=0.585-0.619d1+0.135d12 0.989 5.160×10-3 KB=1.710+0.275d1-0.115d12 0.996 7.783×10-4 KA=0.427-0.369d2 0.964 7.918×10-4 KB=1.764+0.186d2 0.992 3.761×10-4
下载: 导出CSV
-
[1] 郑永来, 杨林德, 李文艺.地下结构抗震[M].上海: 同济大学出版社, 2005: 152-156. [2] Pao Y H. Applied mechanics in science and engineering[J]. Applied Mechanics Review, 1998, 51(2): 141-153. [3] 王长柏, 李海波, 周青春. P波作用下深埋隧道动应力集中问题参数敏感性分析[J].岩土力学, 2011, 32(3): 775-780.Wang Chang-bo, Li Hai-bo, Zhou Qing-chun. Parameters sensitivity analysis of dynamic stress concentration for deep buried tunnel under incident plane waves[J]. Rock and Soil Mechanics, 2011, 32(3): 775-780. [4] 高广运, 李育枢, 李天斌. P波作用下浅埋圆形衬砌隧道动力反应分析[J].中南公路工程, 2007, 32(2): 56-60.Gao Guang-yun, Li Yu-shu, Li Tian-bin. Dynamic analysis of shallow buried circular lining tunnel with vertical incident P wave[J]. Central South Highway Engineering, 2007, 32(2): 56-60. [5] 梁建文, 巴振宁, Lee V W.平面P波在饱和半空间中洞室周围的散射(I):解析解[J].地震工程与工程振动, 2007, 27(1): 1-6.Liang Jian-wen, Ba Zhen-ning, Lee V W. Scattering of plane P waves around a cavity in poroelastic half-space(I): Analytical solution[J]. Journal of Earthquake Engineering and Engineering Vibration, 2007, 27(1): 1-6. [6] 鲍亦兴, 毛昭宙.弹性波的衍射与动应力集中[M].刘殿魁, 苏先樾, 译.北京: 科学出版社, 1993: 321-354. [7] 齐辉, 王艳, 刘殿魁.半无限空间界面附近SH波对圆形衬砌的散射[J].地震工程与工程振动, 2003, 22(3): 41-46.Qi Hui, Wang Yan, Liu Dian-kui. Dynamic analysis of shallow embedded lining structure by incident SH waves[J]. Earthquake Engineering and Engineering Vibration, 2003, 22(3): 41-46. [8] 史文谱, 刘殿魁, 林宏.半无限空间中稳态P波在衬砌周围的散射[J].地震工程与工程振动, 2002, 22(3): 19-26.Shi Wen-pu, Liu Dian-kui, Lin Hong. Scatting of steady P waves around a circular lining in half space[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(3): 19-26. [9] 纪晓东, 梁建文, 杨建江.地下圆形衬砌洞室在平面P波和SV波入射下动应力集中问题的级数解[J].天津大学学报, 2006, 39(5): 511-517.Ji Xiao-dong, Liang Jian-wen, Yang Jian-jiang. On dynamic stress concentration of an underground cylindrical lined cavity subjected to incident plane P and SV waves[J]. Journal of Tianjin University, 2006, 39(5): 511-517. [10] 言志信.爆破地震效应及安全[M].北京: 科学出版社, 2011: 95-107. [11] 肖正学.爆破地震波动力学基础与地震效应[M].成都: 电子科技大学出版社, 2004: 163-171. [12] 何晓群.应用回归分析[M].北京: 中国人民大学出版社, 2007: 72-80. -
计量
- 文章访问数: 2726
- HTML全文浏览量: 372
- PDF下载量: 346
- 被引次数: 0