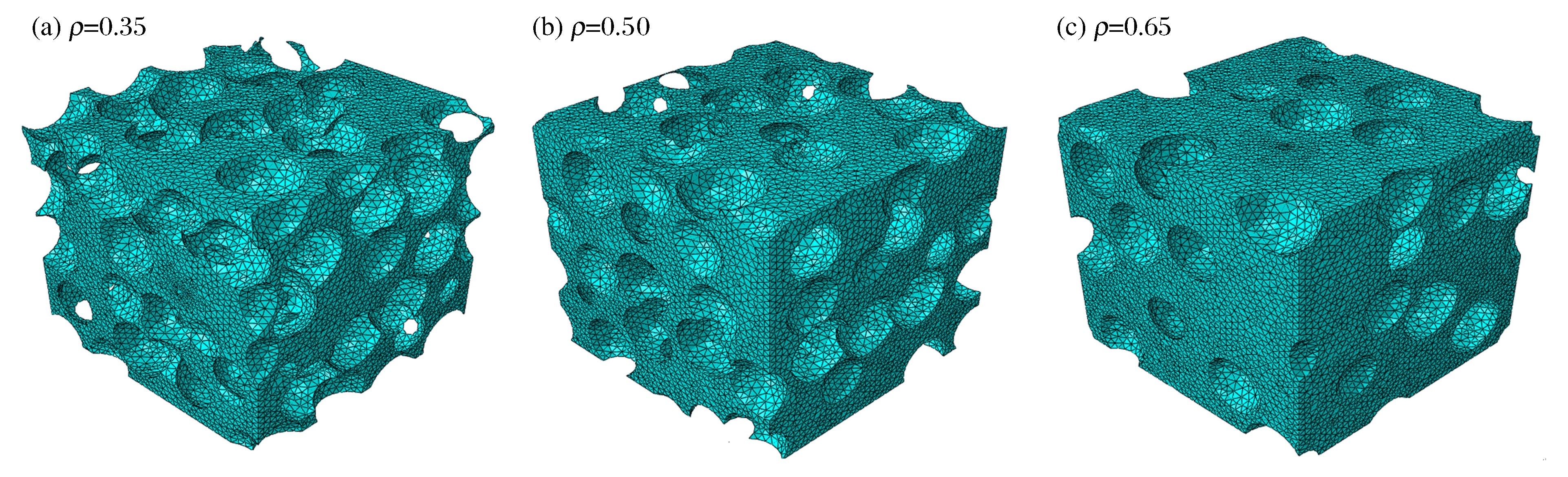
-
摘要: 构建了三维随机分布球形泡孔模型，模拟开、闭孔混合结构泡沫铝材料的微细观结构，并通过有限元方法计算了10~104 s-1应变率范围内、孔隙率35%~65%泡沫铝材料的率相关性以及应变率和相对密度变化对泡沫铝动态压缩力学性能的影响。研究表明：中、低应变率下，泡沫铝材料率相关性能主要取决于基体材料的应变率敏感性；高应变率下，泡沫铝材料率相关性能受基体材料的应变率敏感性以及微结构惯性联合作用，且相对密度较低泡沫铝材料的微结构惯性效应更显著。
-
关键词:
- 固体力学 /
- 率相关 /
- 三维随机球形泡孔模型 /
- 泡沫铝 /
- 有限元
Abstract: To examine the rate-dependent properties of aluminum foams, three-dimensional random spherical cell models were constructed to simulate the microstructures of aluminum foams, and the dynamic deformations of aluminum foams at the strain rates of 10-10 000 s-1 were calculated by using the ANSYS/LS-DYNA commercial code.Obtained results show that at moderate and low strain rates, the rate-dependent properties of aluminum foams originate mainly from the strain-rate sensitivities of their matrix materials.At high strain rates, the rate-dependent properties of aluminum foams are dominated by the combining action of the strain rate sensitivity of cell materials and the microstructure inertia of cells, and the microstructure inertia effects are more remarkable for aluminum foams with low relative density than for those with high relative density. -
图 2 泡沫模型初始弹性模量随相对密度的分布
Figure 2. Initial elastic modulus of foams versus foam relative densities
图 3 基体材料率相关泡沫模型动态压缩应力应变曲线
Figure 3. Dynamic compressive stress-strain curves of foam models with rate-dependent cell material
图 4 基体材料率无关泡沫模型动态压缩应力应变曲线
Figure 4. Dynamic compressive stress-strain curves of foam models with rate-independent cell material
图 5 动态压缩下泡沫铝流动应力与相对密度关系
Figure 5. Flow stresses of aluminum foams versus foam relative densities under dynamic compressive loadings
表 1 拟合结果
Table 1. Fitting results of parameters
${\dot \varepsilon }$/s-1 a n 10 0.698 1.72 100 0.784 1.72 1 000 0.942 1.72 2 500 1.03 1.68 5 000 1.13 1.66 10 000 1.27 1.64 
下载: 导出CSV
表 2 泡沫模型及其基体材料强度的变化
Table 2. Variation of flow stress for foams and its cell material
${{\dot \varepsilon }_2}$/s-1 αf/% αs/% ρ=0.35 ρ=0.50 ρ=0.65 5 000 12.04 11.24 10.66 8.34 10 000 28.59 26.77 25.44 18.25
下载: 导出CSV
-
[1] 卢天健, 何德坪, 陈常青, 等.超轻多孔金属材料的多功能特性及应用[J].力学进展, 2006, 36(4): 517-535.Lu Tian-jian, He De-ping, Chen Chang-qing, et al. The multi-functionality of ultra-light porous metals and their applications[J]. Advances in Mechanics, 2006, 36(4): 517-535. [2] 王永胜, 左孝青, 尹志其, 等.应变率对泡沫铝压缩性能的影响[J].材料导报, 2009, 23(3): 47-52.Wang Yong-sheng, Zuo Xiao-qing, Yin Zhi-qi, et al. Effect of strain rate on compressive property of aluminum foam[J]. Materials Review, 2009, 23(3): 47-52. [3] Deshpande V S, Fleck N A. High strain rate compressive behavior of aluminium alloy foams[J]. International Journal of Impact Engineering, 2000, 24(3): 277-298. [4] 郭伟国, 李玉龙, 黄福增.不同应变率下泡沫铝的形变和力学性能[J].爆炸与冲击, 2008, 28(4): 289-292.Guo Wei-guo, Li Yu-long, Huang Fu-zeng. Deformation and mechanical property of aluminium foam at different strain rates[J]. Explosion and Shock Waves, 2008, 28(4): 289-292. [5] Dannemann K A, Lankford Jr J. High strain rate compression of closed-cell aluminum foams[J]. Materials Science and Engineering: A, 2000, 239(1/2): 157-164. [6] Mukai T, Kanahashi H, Miyoshi T, et al. Experimental study of energy absorption in closed-cell aluminum foam under dynamic loading[J]. Scripta Materialia, 1999, 40(8): 921-927. [7] Mukai T, Miyoshi T, Nakano S, et al. Compressive response of a closed-cell aluminum foam at high st rain rate[J]. Scripta Materialia, 2006, 54(4): 533-537. [8] 程和法.应变率对泡沫Al-Mg合金压缩性能的影响[J].特种铸造及有色合金, 2003, 5: 1-3.Cheng He-fa. The effect of strain rate on the compressive properties of foamed Al-Mg alloy[J]. Special Casting & Nonferrous Alloys, 2003, 5: 1-3. [9] 程和法, 黄笑梅, 王强, 等.通孔泡沫铝的动态压缩行为[J].爆炸与冲击, 2006, 26(2): 169-173.Cheng He-fa, Huang Xiao-mei, Wang Qiang, et al. The dynamic compressive behaviors of an open-cell aluminum foam[J]. Explosion and Shock Waves, 2006, 26(2): 169-173. [10] 田杰, 胡时胜.基体性能对泡沫铝力学行为的影响[J].工程力学, 2006, 23(8): 168-176.Tian Jie, Hu Shi-sheng. Effect of matrix properties of the mechanical behaviors of aluminum foams[J]. Engineering Mechanics, 2006, 23(8): 168-176. [11] 张健, 赵桂平, 卢天健.闭孔泡沫铝应变率效应的试验和有限元分析[J].西安交通大学学报, 2010, 44(5): 97-101.Zhang Jian, Zhao Gui-ping, Lu Tian-jian. Experimental and numerical study on strain rate effects of close-celled aluminum foams[J]. Jounal of Xi'an Jiaotong University, 2010, 44(5): 97-101. [12] 胡时胜, 王悟, 潘艺, 等.泡沫材料的应变率效应[J].爆炸与冲击, 2003, 23(1): 13-18.Hu Shi-sheng, Wang Wu, Pan Yi, et al. Strain rate effect on the properties foam materials[J]. Explosion and Shock Waves, 2003, 23(1): 13-18. [13] Gibson L J, Ashby M F. Cellular solids: Structure and properties[M]. 2nd ed. Cambridge: Cambridge University Press, 1997. -
点击查看大图
计量
- 文章访问数: 3383
- HTML全文浏览量: 340
- PDF下载量: 488
- 被引次数: 0