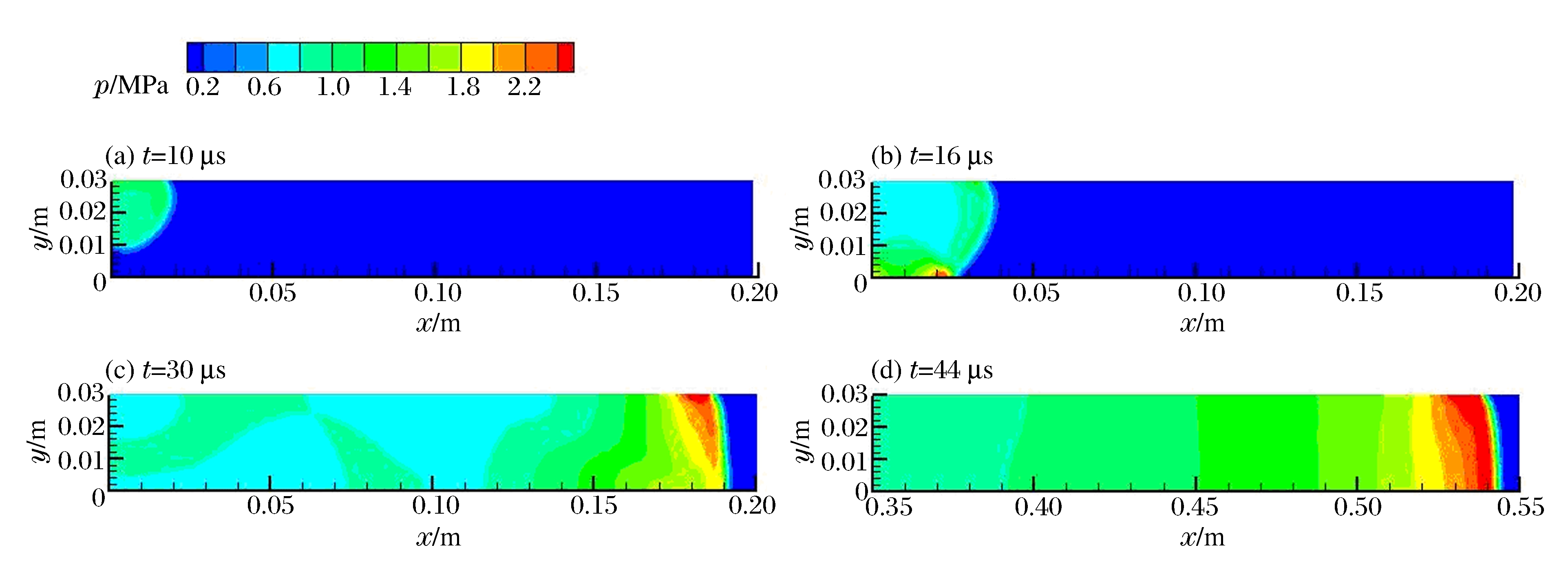
| [1] |
Dreizin E L. Experimental study of aluminum particle flame evolution in normal and micro-gravity[J]. Combustion and Flame, 1999, 116(3): 323-333. http://www.sciencedirect.com/science/article/pii/S0010218097003313
|
| [2] |
Goroshin S, Bidabadi M, Lee J H S. Quenching distance of laminar flame in aluminum dust cIouds[J]. Combustion and Flame, 1996, 105: 147-160. doi: 10.1016/0010-2180(95)00183-2
|
| [3] |
刘晓利, 李鸿志, 郭建国, 等.铝粉-空气混合物燃烧转爆轰(DDT)过程的实验研究[J].爆炸与冲击, 1995, 15(3): 217-228. http://www.cqvip.com/Main/Detail.aspx?id=1693987Liu Xiao-li, Li Hong-zhi, Guo Jian-guo, et al. Deflagration to detonatiion transition(DDT)in aluminum dust-air mixture[J]. Explosion and Shock Waves, 1995, 15(3): 217-228. http://www.cqvip.com/Main/Detail.aspx?id=1693987
|
| [4] |
陈志华, 范宝春, 李鸿志.燃烧管内悬浮铝粉燃烧爆炸过程的研究[J].高压物理学报, 2006, 20(2): 157-162. http://www.cnki.com.cn/Article/CJFDTotal-GYWL200602007.htmChen Zhi-hua, Fan Bao-chun, Li Hong-zhi. Investigations on combustion and explosion of Suspended aluminum particles in a large combustion tube[J]. Journal of High Pressure Physics, 2006, 20(2): 157-162. http://www.cnki.com.cn/Article/CJFDTotal-GYWL200602007.htm
|
| [5] |
李小东, 刘庆明, 白春华, 等.铝粉-空气混合物的燃烧转爆轰过程[J].火炸药学报, 2009, 32(6): 58-61.Li Xiao-dong, Liu Qing-ming, Bai Chun-hua, et al. Deflagration to detonation transition process in aluminum dust-air mixture[J]. Chinese Journal of Explosives & Propellants, 2009, 32(6): 58-61.
|
| [6] |
Veyssiere B, Khasainov B A. Stead, Plane, double-front detonations in gaseous detonable mixtures containing a suspension of aluminum particles[J]. Combustion and Flame, 1991, 85: 241-253. doi: 10.2514/5.9781600865886.0284.0299
|
| [7] |
Fedorov A V, Khmel T A, Fomin V M. Non-equilibrium model of steady detonations in aluminum particles-oxygen suspensions[J]. Shock Waves, 1999, 9(5): 3l3-318. doi: 10.1007/s001930050191
|
| [8] |
韦伟, 翁春生.基于CE/SE方法的铝粉尘爆轰一维两相数值计算[J].南京师范大学学报, 2012, 12(2): 53-56. http://d.wanfangdata.com.cn/Periodical/ddxb201204022Wei Wei, Weng Chun-sheng. One-dimension two-phase-flow numerical simulation of aluminum-dust detonation based on CE/SE method[J]. Journal of Nanjing Normal University, 2012, 12(2): 53-56. http://d.wanfangdata.com.cn/Periodical/ddxb201204022
|
| [9] |
韦伟, 翁春生.基于CE/SE方法的铝粉尘爆轰二维两相数值计算[J].弹道学报, 2012, 24(4): 99-102. http://d.wanfangdata.com.cn/Periodical/ddxb201204022Wei Wei, Weng Chun-sheng. Two-dimension two-phase-flow numerical simulation of aluminum-dust detonation based on CE/SE method[J]. Journal of Ballistics, 2012, 24(4): 99-102. http://d.wanfangdata.com.cn/Periodical/ddxb201204022
|
| [10] |
洪涛, 秦承森.爆轰波管中铝粉尘爆轰的数值模拟[J].爆炸与冲击, 2004, 24(3): 193-200. http://www.cnki.com.cn/article/cjfdtotal-bzcj200403001.htmHong tao, Qin Cheng-sen. Numerical simulation of dust detonation of aluminum powder in explosive tubes[J]. Explosion and Shock Waves, 2004, 24(3): 193-200. http://www.cnki.com.cn/article/cjfdtotal-bzcj200403001.htm
|
| [11] |
洪涛, 秦承森.悬浮铝粉尘爆轰波参数[J].含能材料, 2004, 12(3): 129-133. http://d.wanfangdata.com.cn/Periodical/hncl200403001Hong tao, Qin Cheng-sen. Parameters of detonation in suspended aluminum dust[J]. Chinese Journal of Energetic Materials, 2004, 12(3): 129-133. http://d.wanfangdata.com.cn/Periodical/hncl200403001
|
| [12] |
白桥栋, 翁春生.二维CE/SE方法在内弹道湍流两相流动中的应用[J].兵工学报, 2009, 30(6): 682-687. http://d.wanfangdata.com.cn/Periodical/bgxb200906006Bai Qiao-dong, Weng Chun-sheng. The application of two dimensional space-time conservation element and solution element method(CE/SE)to turbulent two-phase flow in interior ballistics[J]. Acta Armamentarii, 2009, 30(6): 682-687. http://d.wanfangdata.com.cn/Periodical/bgxb200906006
|
| [13] |
Ma Dan-hua, Weng Chun-sheng. Application of two-dimensional viscous CE/SE method in calculation of two-phase detonation[J]. Journal of China Ordnance, 2010, 6(1): 5-9. http://www.cnki.com.cn/Article/CJFDTotal-BAXY201001003.htm
|
| [14] |
翁春生, 王浩.计算内弹道[M].北京: 国防工业出版社, 2006: 276-290.
|







 下载:
下载: