Constitutive model of transparent aviation polyurethane at high strain rates
-
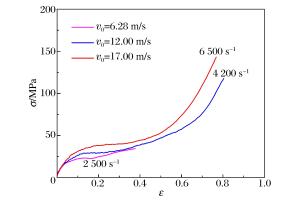
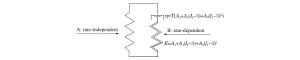
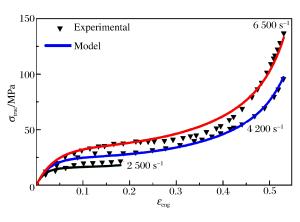
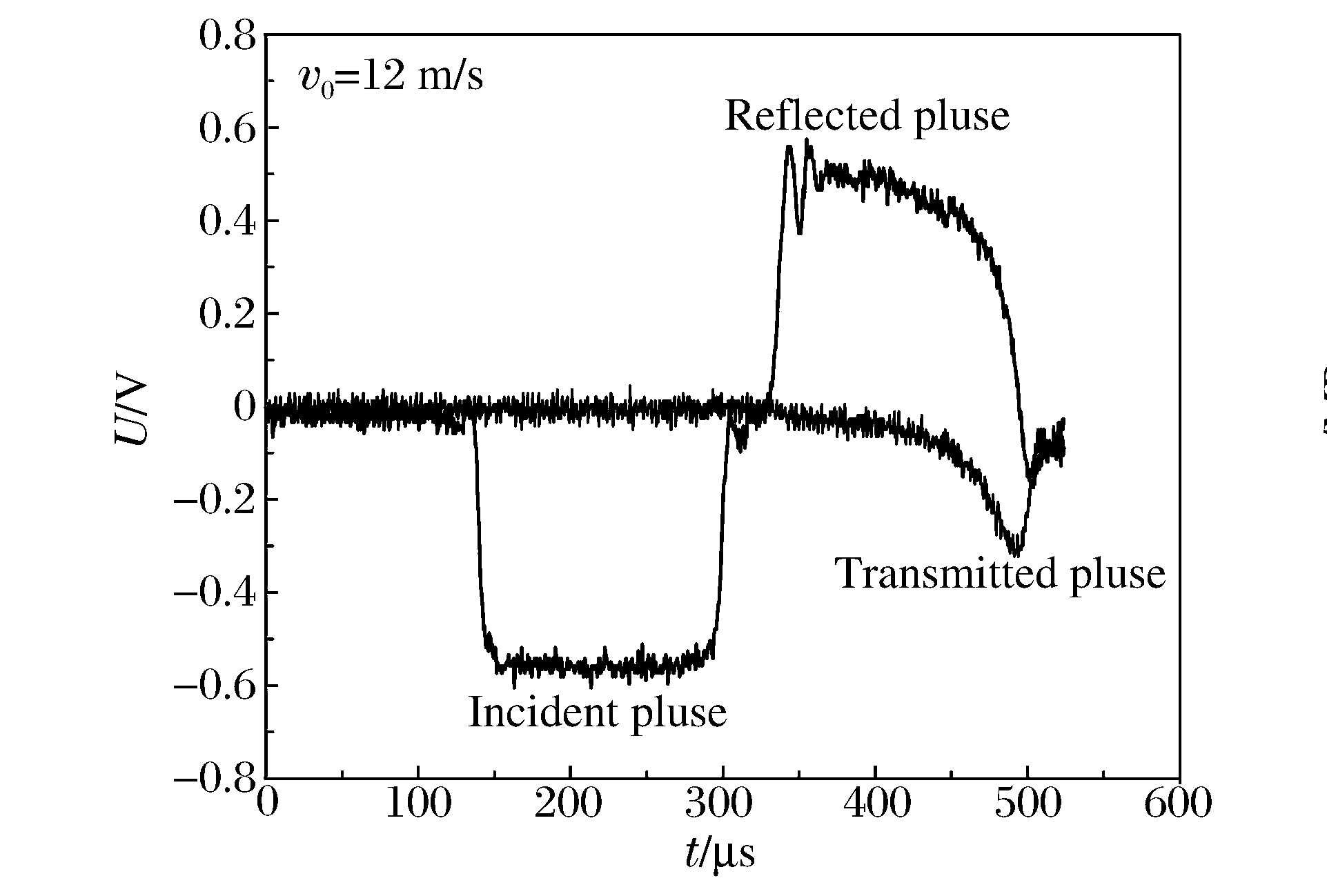
摘要: 采用低阻抗分离式霍普金森压杆对航空透明聚氨酯进行了高应变率下的动态力学性能测试，得到的应力应变曲线表现出了显著的非线性黏弹性特征。基于本构理论和实验数据，构建了航空透明聚氨酯的松弛时间应变相关的超黏弹性本构形式。该本构模型由2部分组成：一部分表征准静态下的超弹性行为，另一部分描述非线性应变率的相关特性。利用超黏弹性本构模型对不同应变率下航空透明聚氨酯的动态应力应变曲线进行拟合，拟合曲线与实验曲线一致性良好。Abstract: The uniaxial compressive properties of aviation polyurethane were investigated experimentally by using a modified aluminum split Hopkinson pressure bar apparatus. The obtained stress-strain curves presented distinct non-linear viscoelastic characteristic.Based on the constitutive theory and the experimental data, a hyper-viscoelastic constitutive model that incorporated a strain-dependent relaxation time was proposed to describe the large compressive deformation response of incompressible aviation polyurethane at high strain rates. The proposed model was made up of two parallel mechanical elements-one component to characterize quasi-static hyperelastic behavior, and the other to define rate-sensitivity and strain history dependence. The predictions of the mechanical behavior using a hyper-viscoelastic constitutive model based on strain energy functions and hereditary approach had a good agreement with experimental results.
-
Key words:
- solid mechanics /
- constitutive model /
- SHPB /
- aviation polyurethane /
- high strain rate /
- hyper-viscoelastic
-
图 2 航空聚氨酯SHPB压缩实验应力应变曲线
Figure 2. True stress-strain curves of the aviation polyurethane
图 4 准静态压缩实验曲线与模型拟合曲线的比较
Figure 4. Comparison between quasi-static curves of experimental data and proposed model
图 5 高应变率压缩实验曲线与模型拟合曲线的比较
Figure 5. Comparison between high strain rates of experimental data and proposed model
表 1 由实验数据拟合确定的模型参量
Table 1. Parameters in proposed stress-strain equations
C10/MPa C01/MPa C11/MPa A1/μs A2 A3/MPa A4/MPa A5/MPa -1.182 -0.069 -0.173 7 0.4 600 -185 45 
下载: 导出CSV
-
[1] Roland C M, Twigg J N, Vu Y, et al. High strain rate mechanical behavior of polyurea[J]. Polymer, 2007, 48(2): 574-578. [2] Yi J, Boyce M C, Lee G F, et al. Large deformation rate-dependent stress-strain behavior of polyurea and polyurethanes[J]. Polymer, 2006, 47(1): 319-329. https://www.sciencedirect.com/science/article/pii/S0032386105015740 [3] Sarva S S, Deschanel S, Boyce M C, et al. Stress-strain behavior of a polyurea and a polyurethane from low to high strain rates[J]. Polymer, 2007, 48(8): 2208-2213. [4] Shim J, Mohr D. Using split Hopkinson pressure bars to perform large strain compression tests on polyurea at low, intermediate and high strain rates[J]. International Journal of Impact Engineering, 2009, 36(9): 1116-1127. [5] Amirkhizi A V, Isaacs J, Mcgee J, et al. An experimentally-based viscoelastic constitutive model for polyurea, including pressure and temperature effects[J]. Philosophical Magazine, 2006, 86(36): 5847-5866. [6] Li C, Lua J. A hyper-viscoelastic constitutive model for polyurea[J]. Materials Letters, 2009, 63(11): 877-880. https://www.sciencedirect.com/science/article/pii/S0167577X09000482 [7] Yang L M, Shim V, Lim C T. A visco-hyperelastic approach to modelling the constitutive behaviour of rubber[J]. International Journal of Impact Engineering, 2000, 24(6): 545-560. [8] Pouriayevali H, Guo Y B, Shim V. A constitutive description of Elastomer behaviour at high strain rates-A strain-dependent relaxation time approach[J]. International Journal of Impact Engineering, 2012, 47: 71-78. https://www.sciencedirect.com/science/article/pii/S0734743X12000760 [9] Chen W, Zhang B, Forrestal M J. A split Hopkinson bar technique for low-impedance materials[J]. Experimental Mechanics, 1999, 39(2): 81-85. [10] 林玉亮, 卢芳云, 卢力.高应变率下硅橡胶的本构行为研究[J].高压物理学报, 2007, 21(3): 289-294.Lin Yu-liang, Lu Fang-yun, Lu Li. Constitutive behaviors of a silicone rubber at high strain rates[J]. Chinese Journal of High Pressure Physics, 2007, 21(3): 289-294. [11] 王礼立.冲击动力学进展[M].合肥: 中国科学技术大学出版社, 1992. [12] Rivlin R S. Collected papers of R. S. Rivlin[M]. Berlin: Springer, 1997. [13] Hoo Fatt M S, Xin O. Integral-based constitutive equation for rubber at high strain rates[J]. International Journal of Solids and Structures, 2007, 44(20): 6491-6506. 期刊类型引用(12)
1. 包健，马贵辉，孙龙泉，陈惟楚，李明. 带椭球形气囊航行体落水-上浮过程仿真. 兵工学报. 2024(01): 206-218 . 
百度学术2. 职明洋，燕国军，孙龙泉，王鹏霄. 带气囊结构航行体入水回收动力学特性研究. 力学学报. 2024(04): 943-959 . 百度学术3. 郑伟，李强，范旭东，吕续舰. 跨介质航行器高速入水降载方法研究综述. 水下无人系统学报. 2024(03): 411-425 . 百度学术4. 彭睿哲，冯和英，向敏，彭叶辉. 头部喷气对跨介质航行体入水过程载荷特性的影响. 舰船科学技术. 2024(13): 59-66 . 百度学术5. 程时锃，陈浩，梁晶，胡慕秋，张凯. 跨介质滑翔器机翼设计与气动特性数值模拟. 舰船科学技术. 2024(19): 92-99 . 百度学术6. 王占莹，权晓波，段金雄，孙铁志. 波浪环境下带助浮装置航行体落水冲击流场及运动特性研究. 爆炸与冲击. 2024(11): 141-158 . 
本站查看7. 王聪，许海雨，卢佳兴. 跨介质航行器入水多相流场及运动特性研究现状与展望. 水下无人系统学报. 2023(01): 38-49 . 百度学术8. 黄恩光，彭辉，毛龙，杨威，郑强，姚俊，余维维. 某型气囊充气展开过程研究. 包装工程. 2022(03): 169-174 . 百度学术9. 施瑶 ，刘振鹏 ，潘光 ，高兴甫 . 航行体梯度密度式头帽结构设计及降载性能分析. 力学学报. 2022(04): 939-953 . 百度学术10. 施瑶，刘振鹏，潘光，高兴甫. 航行体开槽包裹式缓冲头帽结构设计及其降载性能. 爆炸与冲击. 2022(12): 95-107 . 本站查看11. 薛齐文，王霄腾，何宜谦，郭敏，刘旭东，鄂智佳. 不同折叠形式的柱状气囊展开过程数值模拟. 航空工程进展. 2021(03): 161-170 . 百度学术12. 杨威，屈纯，毛龙，舒君玲，牛同锋，姚俊. 气囊压力对跌倒防护气囊缓冲效果的实验研究. 应用力学学报. 2021(04): 1738-1744 . 百度学术其他类型引用(12)
-
百度学术
图(5) / 表(1)
计量
- 文章访问数: 4821
- HTML全文浏览量: 583
- PDF下载量: 798
- 被引次数: 24