Progress in high-power laser ramp compression of solids
-
摘要: 利用高功率激光诱导的应力波对固体材料进行高应变率斜波压缩，是近年来快速发展的新型动高压实验技术。与传统加载手段不同，它可以在数ns时间内以极高的应变率(106~109 s-1)将薄样品平滑加载到数千万大气压，并仍然保持其固体状态。结合多种先进的诊断技术，可以测得样品材料的热力学、动力学参数和原位微观结构特性，是研究动高压物理、物态方程和高应变率动力学问题的先进途径。本文梳理了这种技术的发展历程，对其加载和诊断技术以及已取得的主要结果进行综述，并展望了其发展前景。Abstract: Laser-induced stress waves can deliver ramp compression on solid materials with very high strain rates, and it is one of the newly-developed dynamic high-pressure methods in decades. Distinct from the conventional methods, laser ramp compression can reach terapascal pressures smoothly from ambient pressure with a high strain rate 106-109 s-1, but the sample is still in solid state. During the rapid loading process, the thermodynamic state, dynamic characteristics, and in situ microstructure can all be probed by the advanced diagnostic technology. This method is becoming an important and new approach to further investigation on high-pressure physics, equation of state, and rate-dependent material dynamics. In this paper, the history, principle, diagnostics and main breakthroughs of laser ramp compression are reviewed and expected.
-
Key words:
- mechanics of explosion /
- ramp compression /
- high-power laser /
- solids /
- equation of state /
- rate dependent
-
随着近年来世界各地恐怖事件的不断发生，大批学者对地下防御工事的相关问题进行了大量研究[1-4]。典型空腔环境内爆炸效应研究就是这类问题中重要的一项，这项研究包括对空腔环境壁面上爆炸载荷分布规律和结构振动等问题的研究，其实质是为典型空腔环境的强度设计提供依据。目前，对这类问题的研究主要采用3种方法:理论计算、数值模拟和模型实验[5-8]。由于空腔环境内爆炸流场形成过程复杂，因此在理论推导过程中很难建立一个合理的数学模型来求得精确的解析解；数值模拟的优点在于可以再现空腔环境内爆炸冲击波流场的演变过程，缺点则是很难找到与材料吻合的计算参数，因此会导致计算结果产生一定的误差，同时数值模拟要求网格划分得十分细致，这也对计算机硬件提出了很高的要求；模型实验则可以通过分析实测曲线的峰值和波形来得到较精确的结论。目前空腔环境内爆炸模型实验大多是在已有的爆炸塔或爆炸罐中进行的，而本文中拟根据工程中的具体要求设计一套实验装置，通过实验现象和实测的实验数据分析爆炸载荷的分布规律和模型结构的破坏形式，以期为下一步各类密闭腔室环境内爆炸效应问题的研究提供理论依据。
1. 空腔环境实验模型设计
1.1 单腔室空腔环境
根据国防工事和人防工事的等级设计规范[9]，空腔环境内防护单元隔墙的等效静载荷是爆炸冲击波超压峰值的1/4~1/8，考虑到本次的实验模型要能进行多次实验，所以设计防护单元隔墙的等效静载荷为爆炸冲击波超压，即防护单元隔墙的等效静载荷为1.2 MPa。
根据在钢筋混凝土结构设计中纵向受力钢筋的配置要求[10]，本文的实验模型可以简化为内部静压为1.2 MPa的长方体钢筋混凝土密闭腔室，腔室的主体采用C35级混凝土，钢筋采用HRB400级螺纹钢筋，钢筋的尺寸、数量和间隔根据混凝土设计规范进行计算。由于爆炸冲击波超压均匀作用在腔室的内壁上，因此钢筋混凝土结构的侧壁在纵向受拉伸作用，且整个构建处于轴心受拉状态。轴心受拉构建在破坏时所能承受的拉力可由下式求得：
N≤fyAs (1) 式中：N为轴向拉力设计值，fy为钢筋抗拉强度设计值，As为纵向受拉钢筋截面面积。
实验模型结构采用对称配筋，根据承载力极限(Nu)状态设计法的基本原则及平衡条件, 可得：
N≤Nu/γd=fyAs/γd (2) 所需钢筋总横截面积为：
As=γdN/fy (3) 式中：γd为结构因数；查表得HRB400钢筋的fy=400 MPa。
此外，最小配筋率还要求：As≥0.4%S以及As≥90ftS/fy，ft为混凝土抗拉强度设计值，查表[11]得C35混凝土的ft=1.57 MPa。
根据以上的混凝土设计要求，计算得到的结果见表 1，表中ps, e为等效静载荷，a为结构的长度，b为结构的宽度，c为结构的高度，S为结构内表面积，l为结构壁面周长，F为钢筋拉力，f为钢筋强度，d为钢筋直径，n为钢筋根数，δ为钢筋层数，k为钢筋间隔。
表 1 结构壁面纵向钢筋参数Table 1. Reinforcement parameters of longitudinal wallps, e/MPa a/m b/m c/m S/dm2 l/m F/MN f/MPa d/mm n δ k/mm 1.2 3 1.5 1.5 450 9 5.4 400 14 88 1 102 1.2 3 1.5 1.5 450 9 5.4 400 14 88 2 204 表 1是根据静压力在结构壁面上的作用力计算得到的数值，根据等效静载荷是爆炸冲击波超压峰值的1/8~1/4，保守估计该壁面上可以承受2.4~3.6 MPa的爆炸冲击载荷，由冲击波在刚性壁面上的反射超压经验公式[12]：
Δp2=2Δp1+6Δp21Δp1+7p0 (4) 可以得到入射波的超压值为0.56~0.80 MPa，式中：Δp2为冲击波的反射超压，Δp1为冲击波的入射超压，p0为标准大气压。再由萨多夫空爆经验公式[13]：
p={1.07Z3−0.1Z≤10.076Z+0.255Z2+0.65Z31<Z≤1.5 (5) 可以得出实验中的最大药量至少可达200 g，式中：Z=RW-1/3, R为特征点距离爆心的距离(m)，W为炸药的质量(kg)。
单腔室密闭结构采用C35级混凝土和直径14 mm的HRB400级钢筋; 内腔长、宽、高分别为3000、1500、1500 mm，壁厚150 mm。钢筋在结构厚度方向双层排列，间隔100 mm；在结构长度方向钢筋排列16层，间隔为190 mm；在结构宽、高度方向钢筋排列8层，间隔也为190 mm，具体结构见图 1~2。
1.2 实验测量设备
实验中采用CY-YD-205型压力传感器捕捉压力信号，传感器的量程为0~5 MPa，压力高于0.1 MPa时立即触发。整个实验模型中共布置5个观测点，分别设置在2个相邻的侧墙壁面上，传感器安放在实验装置侧墙的预留孔内，并确保传感器的压力感受面与实验装置内壁平齐，具体位置如图 3所示。
图 3 观测点即压力传感器安装具体位置示意图(单位为mm)Figure 3. Schematic layout of pressure sensors (observation points) (unit in mm)1.3 爆炸源
共进行了5次空腔环境内爆炸实验，爆炸源分2种:一种是单块质量为75 g的圆柱状TNT炸药，另外一种是单块质量为200 g的块状TNT炸药，用铝制8号电雷管起爆，每一发实验的装药位置均在实验装置的中心处，实验药柱如图 4所示。
2. 实验结果
2.1 实测的爆炸载荷波形
每一发实验后传感器都记录下壁面上5个观测点的压力时程曲线，从实测的冲击波波形来看，实验装置角域处传感器波形较乱，其他位置传感器的实测波形较规则。
针对药量为75 g的情况共进行了3次模型实验，图 5给出了3次实验中相邻壁面上5个观测点的实测压力(p)时程曲线和数值模拟曲线。从图 5可以看出，作用在结构壁面上的爆炸载荷，初始为脉冲载荷，其峰值超压较大，而作用时间较短，脉冲有多个，一般情况下脉冲峰值呈锯齿形依次迅速降低，此后形成准静态压力，上述特点在图 5(a)中体现得最明显，观测点的首次压力峰值达到1.38 MPa，比解析解[14](自由大气空爆相应比例距离爆炸处反射压力峰值)高约64%；在结构壁面上的某些区域，由于空腔环境壁面的约束作用使大量冲击波叠加，爆炸流场变得相当复杂，其后续峰值甚至会超过初始脉冲峰值，这一特点在图 5(b)中体现得最明显，观测点的首个压力峰值为0.19 MPa，而最大压力出现在第4个波峰，其最大值为1.71 MPa，是首个峰值的9倍。
.png)
5(a) 观测点1的实测冲击波波形5(a). Overpressure-time curves of shock waves measured at observation point 1.png)
5(b) 观测点2的实测冲击波波形5(b). Overpressure-time curves of shock waves measured at observation point 2.png)
5(c) 观测点3的实测冲击波波形5(c). Overpressure-time curves of shock waves measured at observation point 3.png)
5(d) 观测点4的实测冲击波波形5(d). Overpressure-time curves of shock waves measured at observation point 4.png)
5(e) 观测点5的实测冲击波波形5(e). Overpressure-time curves of shock waves measured at observation point 5表 2展示了不同药量下理论计算、数值模拟和实测数据的对比。
表 2 5个观测点首次反射的理论计算、数值模拟及实测结果的比较Table 2. Comparison among theoretical calculation, numerical simulation and experimental results for the first reflection at five observation pointsW/g 方法 p/MPa 观测点1 观测点2 观测点3 观测点4 观测点5 理论计算 1.059 0.164 0.441 0.135 0.135 75 数值模拟 0.752 0.103 0.304 0.094 0.091 实验平均值 1.154 0.165 0.450 0.107 0.148 理论计算 2.212 0.285 0.836 0.225 0.229 150 数值模拟 1.553 0.183 0.574 0.146 0.157 实验平均值 1.960 0.263 0.804 0.181 0.450 理论计算 3.025 0.367 1.108 0.282 0.290 200 数值模拟 2.102 0.234 0.754 0.176 0.201 实验平均值 2.104 0.336 0.556 0.346 0.759 从表 2可以看出，首个峰值理论计算、数值模拟和实测结果之间存在一定的误差，造成这种误差的原因有很多。如在数值模拟研究方面, 目前爆炸类问题一般采用LS-DYNA软件，该程序具有Lagrange、Euler和ALE算法，这3种算法得到的计算结果存在着一定的差异：拉格朗日算法由于计算网格的畸变，可能直接影响计算精度甚至使计算终止；欧拉算法则网格数量过大，会占用很多的计算机资源；ALE算法采用了Lagrange和Euler两种算法执行自动重分区，即执行一步或者几步Lagrange计算，当单元网格随材料流动产生变形时再执行ALE计算。同样网格的划分对计算结果也存在一定的影响，T.C.Chapman等[15]在计算冲击波超压时，发现计算网格长度由10 mm缩减到1 mm时，计算结果可提高24.6%。由此可见，计算方法、网格划分、计算机硬件条件等因素将直接决定计算结果的准确性。而在实验方面，单腔室箱体的密封性、传感器的安装位置以及炸药的装药形状等因素也都会对实验结果造成一定的影响。以观测点1和观测点2这2个正反射点为例，与理论计算相比较，数值模拟的误差在30%左右，而实测结果的误差则在10%左右。
2.2 结构破坏形式
2.2.1 实验现象
由于实验是在密闭单腔室内进行，且结构密封性较好，因此炸药爆炸释放的能量大部分转化为对结构模型的冲击能，并且作用时间很长。当药量为75 g时，模型结构几乎未见明显裂纹，炸药对结构的破坏效应不大。当药量增加到150 g时，实验装置顶部表面出现裂纹，裂纹主要出现在爆心投影点周围。当药量增加到200 g时，炸药对模型的破坏作用较明显，顶部裂纹进一步增加，裂纹最宽处可达到1 cm，裂纹长达到3 m，打开实验装置门后发现结构侧壁和顶部连接处出现较严重的开裂，结构侧壁有明显的弯曲变形，局部混凝土被压碎脱落。造成这一现象的主要原因是：混凝土承受爆炸载荷作用前已经含有一些微小裂纹，在爆炸载荷作用下微小裂纹萌生、扩展、贯通，直至产生宏观裂纹，并逐渐失去了承载能力。图 6给出了200 g炸药爆炸后结构模型的破坏情况。
图 6 200 g装药爆炸后结构模型的破坏情况Figure 6. Destruction of the model after explosion of 200 g TNT2.2.2 加速度曲线分析
以75 g药量为例，对壁面上几个观测点进行简单的振动分析，图 7给出了实验中几个观测点加速度的实测曲线。
图 7 75 g装药爆炸后不同观测点的加速度时程曲线Figure 7. Acceleration-time curves at different observation points after explosion of 75 g TNT从图 7可以看出，观测点1的振动加速度最大，达到了400个重力加速度，这一结果与实验现象也较吻合，装置出现较大裂纹处主要集中在爆心投影点周围，即观测点1；从实测的压力时程曲线可知，观测点2出现了多个超压峰值，这是由于空腔环境内爆炸冲击波流场的叠加造成的，因此观测点2的振动加速度也体现出了多个峰值的特点。
3. 结语
(1) 在结构壁面上的某些区域爆炸载荷的分布规律与W.E.Baker等[16]提出的内爆炸载荷的多三角形脉冲算法基本一致，初始为脉冲载荷，其峰值超压较大，而作用时间较短，脉冲有多个，一般情况下脉冲峰值呈锯齿形依次迅速降低，此后形成准静态压力；而壁面上的另一些区域由于受到密闭腔室壁面的约束作用，爆炸冲击波大量叠加使得爆炸流场十分复杂，因此出现了后续冲击波峰值会超过初始脉冲峰值的现象，用于描述这一现象的数学模型还有待进一步研究。
(2) 当炸药对结构的破坏作用达到一定程度时，结构各个壁面有明显的弯曲变形，爆心投影处会向外鼓胀，按照塑性铰线形式的破坏行为是箱体结构内爆炸破坏的特点[17]；结构模型角域附近由于冲击波的汇聚作用，因此与其他部位相比更容易被破坏，实验中可以看到侧墙和顶部连接处会出现明显的长条裂纹，在今后的结构强度设计中应引起重视。
-
-
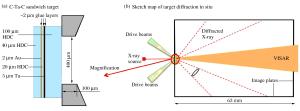
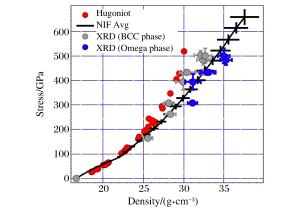
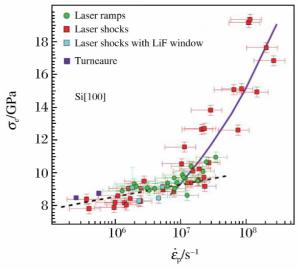
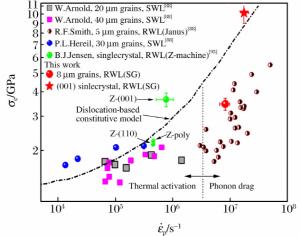
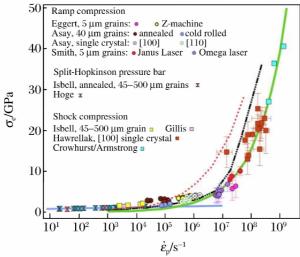
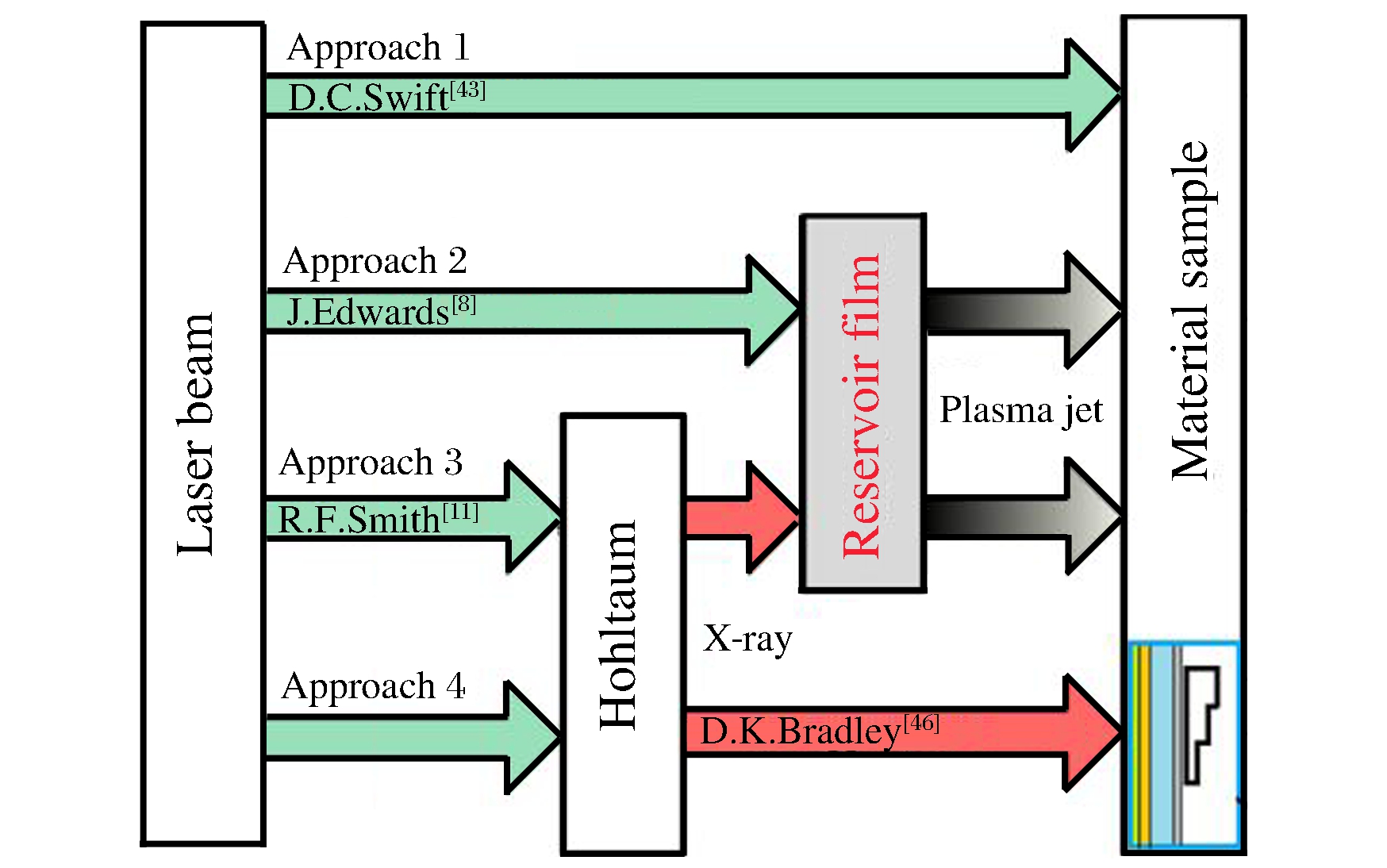
[1] Van Kessel C G M, Sigel R. Observation of laser-driven shock waves in solid hydrogen[J]. Physical Review Letters, 1974, 33(17):1020-1023. http://adsabs.harvard.edu/abs/1974PhRvL..33.1020V [2] Salzmann D, Eliezer S, Krumbein A D, et al. Laser-driven shock-wave propagation in pure and layered targets[J]. Physical Review A, 1983, 28(3):1738-1751. http://adsabs.harvard.edu/abs/1983PhRvA..28.1738S [3] Cauble R, Phillion D W, Hooveret T J, et al. Demonstration of 0.75 Gbar planar shocks in x-ray driven colliding foils[J]. Physical Review Letters, 1993, 70(14):2102-2105. http://www.ncbi.nlm.nih.gov/pubmed/10053471 [4] Swift D, Hawreliak J, Braun D, et al. Gigabar material properties experiments on NIF and Omega[C]//Elert M L, Buttler W T, Borg J P, et al. Shock Compression of Condensed Matter-2011: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Chicago: the American Physical Society, 2011. [5] Lindl J D, Amendt P, Berger R L, et al. The physics basis for ignition using indirect-drive targets on the National Ignition Facility[J]. Physics of Plasmas, 2004, 11(2):339. http://www.tandfonline.com/servlet/linkout?suffix=CIT0002&dbid=16&doi=10.1080%2F09500340.2015.1075619&key=10.1063%2F1.1578638 [6] Munro D H, Celliers P M, Collins G W, et al. Shock timing technique for the National Ignition Facility[J]. Physics of Plasmas, 2001, 8(5):2245. doi: 10.1063/1.1347037 [7] Shigemori K, Shimizu K, Nakamoto Y, et al. Multiple shock compression of diamond foils with a shaped laser pulse over 1 TPa[J]. Journal of Physics: Conference Series, 2008, 112(4):042023. http://adsabs.harvard.edu/abs/2008JPhCS.112d2023S [8] Edwards J, Lorenz K T, Remington B A, et al. Laser-driven plasma loader for shockless compression and acceleration of samples in the solid state[J]. Physical Review Letters, 2004, 92(7):075002. http://www.ncbi.nlm.nih.gov/pubmed/14995863 [9] Li Mu, Zhang Hong-ping, Sun Cheng-wei, et al. Numerical analysis of laser-driven reservoir dynamics for shockless loading[J]. Journal of Applied Physics, 2011, 109(9):093525. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5770336 [10] Hawreliak J, Colvin J, Eggert J, et al. Modeling planetary interiors in laser based experiments using shockless compression[J]. Astrophysics and Space Science, 2007, 307(1/2/3):285-289. doi: 10.1007/s10509-007-9385-z [11] Smith R F, Eggert J H, Jankowski A, et al. Stiff response of aluminum under ultrafast shockless compression to 110 GPa[J]. Physical Review Letters, 2007, 98(6):065701. http://europepmc.org/abstract/MED/17358956 [12] Smith R F, Pollaine S M, Moon S J, et al. High planarity x-ray drive for ultrafast shockless-compression experiments[J]. Physics of Plasmas, 2007, 14(5):057105. doi: 10.1063/1.2712450 [13] Miyanishi K, Ozaki N, Brambrink E, et al. Characterization of laser-driven ultrafast shockless compression using gold targets[J]. Journal of Applied Physics, 2014, 116(4):043521 doi: 10.1063/1.4891802 [14] Eggert J H, Hicks D G, Celliers P M, et al. Melting temperature of diamond at ultrahigh pressure[J]. Nature Physics, 2010, 6(1):40-43. http://www.nature.com/nphys/journal/v6/n1/abs/nphys1438.html [15] Spaulding D K, McWilliams R S, Jeanloz R, et al. Evidence for a phase transition in silicate melt at extreme pressure and temperature conditions[J]. Physical Review Letter, 2012, 108(6):065701. http://www.ncbi.nlm.nih.gov/pubmed/22401087 [16] McWilliams R S, Spaulding D K, Eggert J H, et al., Phase transformations and metallization of magnesium oxide at high pressure and temperature[J]. Science, 2012, 338(6112):1330-1333. http://www.bionity.com/en/publications/495318/report-phase-transformations-and-metallization-of-magnesium-oxide-at-high-pressure-and-temperature.html [17] Luo S N, Swift D C, Tierney T E, et al. Laser-induced shock waves in condensed matter: Some techniques and applications[J]. High Pressure Research, 2004, 24(4):409-422. http://adsabs.harvard.edu/abs/2004HPR....24..409L [18] Kalantar D H, Belak J F, Collins G W, et al. Direct observation of the α-ε transition in shock-compressed iron via nanosecond x-ray diffraction[J]. Physical Review Letters, 2005, 95(7):075502. http://adsabs.harvard.edu/cgi-bin/nph-data_query?bibcode=2005PhRvL..95g5502K&db_key=PHY&link_type=EJOURNAL [19] Gotchev O V, Chang P Y, Knauer J P, et al. Laser-driven magnetic-flux compression in high-energy-density plasmas[J]. Physical Review Letter, 2009, 103(21):215004. http://www.ncbi.nlm.nih.gov/pubmed/20366046 [20] Collins G. Physics of dense matter[C]//Proceedings of the 2013 HEDP Summer School. Ohio State University, 2013. [21] Benuzzi A, Löwer T, Koenig M, et al. Indirect and direct laser driven shock waves and applications to copper equation of state measurements in the 10-40 Mbar pressure range[J]. Physical Review E, 1996, 54(2):2162-2165. http://www.ncbi.nlm.nih.gov/pubmed/9965306 [22] Cottet F, Romain J P, Fabbro R, et al. Ultrahigh-pressure laser-driven shock-wave experiments at 0.26 μm wavelength[J]. Physical Review Letters, 1984, 52(21):1884-1886. http://adsabs.harvard.edu/abs/1984PhRvL..52.1884C [23] Trainor R J, Holmes N C, Anderson R A, et al. Shock wave pressure enhancement using short wavelength (0.35 μm) laser irradiation[J]. Applied Physics Letters, 1983, 43(6):542-544. doi: 10.1063/1.94412 [24] Fu Si-zu, Huang Xiu-guang, Ma Min-xun, et al. Analysis of measurement error in the experiment of laser equation of state with impedance-match way and the Hugoniot data of Cu up to ~2.24 TPa with high precision[J]. Journal of Applied Physics, 2007, 101(4):043517. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4942823 [25] Celliers P M, Collins G W, Silva L B D, et al. Accurate measurement of laser-driven shock trajectories with velocity interferometry[J]. Applied Physics Letters, 1998, 73(10):1320. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4898858 [26] Bradley D K, Eggert J H, Hicks D G, et al. Shock compressing diamond to a conducting fluid[J]. Physical Review Letters, 2004, 93(19):195506. http://www.ncbi.nlm.nih.gov/pubmed/15600850 [27] Celliers P M, Bradley D K, Collins G W, et al. Line-imaging velocimeter for shock diagnostics at the OMEGA laser facility[J]. Review of Scientific Instruments, 2004, 75(11):4916. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5011353 [28] Celliers P M, Collins G W, Hicks D G, et al. Electronic conduction in shock-compressed water[J]. Physics of Plasmas, 2004, 11(8):41-44. doi: 10.1063/1.1758944 [29] Hicks D G, Boehly T R, Celliers P M, et al. Shock compression of quartz in the high-pressure fluid regime[J]. Physics of Plasmas, 2005, 12(8):082702. doi: 10.1063/1.2009528 [30] Miller J E, Boehly T R, Melchior A, et al. Streaked optical pyrometer system for laser-driven shock-wave experiments on OMEGA[J]. Review of Scientific Instruments, 2007, 78(3):034903. doi: 10.1063/1.2712189 [31] Hicks D G, Boehly T R, Celliers P M, et al. Laser-driven single shock compression of fluid deuterium from 45 to 220 GPa[J]. Physical Review B, 2009, 79(1):014112. http://adsabs.harvard.edu/abs/2009PhRvB..79a4112H [32] Jeanloz R, Celliers P M, Collins G W, et al. Achieving high-density states through shock-wave loading of precompressed samples[J]. Proceedings of the National Academy of Sciences, 2007, 104(22):9172-9177. doi: 10.1073/pnas.0608170104 [33] Eggert J, Brygoo S, Loubeyre P, et al. Hugoniot data for helium in the ionization regime[J]. Physical Review Letters, 2008, 100(12):124503. http://www.ncbi.nlm.nih.gov/pubmed/18517873 [34] Loubeyre P, Brygoo S, Eggert J, et al. Extended data set for the equation of state of warm dense hydrogen isotopes[J]. Physical Review B, 2012, 86(14):144115. http://adsabs.harvard.edu/abs/2012PhRvB..86n4115L [35] Brygoo S, Henry E, Loubeyre P, et al. Laser-shock compression of diamond and evidence of a negative-slopemelting curve[J]. Nature Materials, 2007, 6(4): 274-281. http://europepmc.org/abstract/MED/17384637 [36] Knudson M D, Desjarlais M P. Adiabatic release measurements in α-quartz between 300 and 1200 GPa: Characterization of α-quartz as a shock standard in the multimegabar regime[J]. Physical Review B, 2013, 88(18):184107. http://adsabs.harvard.edu/abs/2013PhRvB..88r4107K [37] Ozaki N, Sano T, Ikoma M, et al. Shock Hugoniot and temperature data for polystyrene obtained with quartz standard[J]. Physics of Plasmas, 2009, 16(6):062702. doi: 10.1063/1.3152287 [38] Knudson M D, Desjarlais M P. Shock compression of quartz to 1.6 TPa: Redefining a pressure standard[J]. Physical Review Letters, 2009, 103(22):225501. http://www.ncbi.nlm.nih.gov/pubmed/20366104 [39] Eggert J H. Materials at extreme compression[R]. Report No. LLNL-CONF-655773, 2014. [40] 孙承纬, 赵剑衡, 王桂吉, 等.磁驱动准等熵平面压缩和超高速飞片发射实验技术原理、装置及应用[J].力学进展, 2012, 42(2):206-218. http://d.wanfangdata.com.cn/Periodical/lxjz201202008Sun Cheng-wei, Zhao Jian-heng, Wang Gui-ji, et al. Progress in magentic loading techniques for isentropic compression experiments and ultra-high velocity flyer launching[J]. Advances in Mechanics, 2012, 42(2):206-218. http://d.wanfangdata.com.cn/Periodical/lxjz201202008 [41] Smith R F, Eggert J H, Jeanloz R, et al. Ramp compression of diamond to five terapascals[J]. Nature, 2014, 511(7509):330-333. http://europepmc.org/abstract/MED/25030170 [42] Cauble R, Reisman D B, Asay J R, et al. Isentropic compression experiments to 1 Mbar using magnetic pressure[J]. Joural of Physics: Condensed Matter, 2002, 14:10821-10824. http://www.ingentaconnect.com/search/article?option1=tka&value1=Isentropic+compressibilities&pageSize=10&index=2 [43] Swift D C, Johnson R P. Quasi-isentropic compression by ablative laser loading: Response of materials to dynamic loading on nanosecond time scales[J]. Physical Review, 2005, 71(6):066401. http://www.ncbi.nlm.nih.gov/pubmed/16089874 [44] Amadou N, Brambrink E, Benuzzi-Mounaix A N, et al. Direct laser-driven ramp compression studies of iron: A first step toward the reproduction of planetary core conditions[J]. High Energy Density Physics, 2013, 9(2):243-246. http://www.sciencedirect.com/science/article/pii/S1574181813000098 [45] Koenig M, Benuzzi-Mounaix A, Brambrink E, et al. Simulating earth core using high energy lasers[J]. High Energy Density Physics, 2000, 6(2):210-214. http://www.sciencedirect.com/science/article/pii/S1574181809001256 [46] Bradley D K, Eggert J H, Smith R F, et al. Diamond at 800 GPa[J]. Physical Review Letters, 2009, 102(7):075503. http://europepmc.org/abstract/MED/19257686 [47] Xue Quan-xi, Wang Zhe-bin, Jiang Shao-en, et al. Laser-direct-driven quasi-isentropic experiments on aluminum[J]. Physics of Plasmas, 2014, 21(7):072709. doi: 10.1063/1.4890851 [48] Wang J, Smith R F, Eggert J H, et al. Ramp compression of iron to 273 GPa[J]. Journal of Applied Physics, 2013, 114(2):023513. doi: 10.1063/1.4813091 [49] Wang J, Smith R F, Coppari F, et al. Ramp compression of magnesium oxide to 234 GPa[J]. Journal of Physics: Conference Series, 2014, 500(6):062002. http://meetings.aps.org/link/BAPS.2013.SHOCK.H5.4 [50] Eggert J. Ramp-compression experiments on tantalum at the NIF and Omega lasers[R]. Report Number: LLNL-CONF-490363, 2011. [51] Eggert J. Overview of NIF TARDIS shots[R]. Report Number: LLNL-CONF-653683, 2014. [52] Swift D C, Kraus R G, Loomis E N, et al. Shock formation and the ideal shape of ramp compression waves[J]. Physical Review E, 2008, 78:066115. http://europepmc.org/abstract/MED/19256913 [53] Jin Yun-sheng, Sun Cheng-wei, Zhao Jian-heng, et al. Optimization of loading pressure waveforms for piston driven isentropic compression[J]. Journal of Applied Physics, 2014, 115(24):243506. http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6846238&url=http%3A%2F%2Fieeexplore.ieee.org%2Fstamp%2Fstamp.jsp%3Ftp%3D%26arnumber%3D6846238 [54] Xue Quan-xi, Wang Zhe-bin, Jiang Shao-en, et al. Characteristic method for isentropic compression simulation[J]. AIP Advances, 2014, 4(5):057127. doi: 10.1063/1.4880039 [55] Shu Hua, Fu Si-zu, Huang Xiu-guang, et al. Plastic behavior of aluminum in high strain rate regime[J]. Journal of Applied Physics, 2014, 116(3):033506. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6857956 [56] Lorenz K T, Edwards M J, Glendinning S G, et al. Accessing ultrahigh-pressure, quasi-isentropic states of matter[J]. Physics of Plasmas, 2005, 12(5):056309. doi: 10.1063/1.1873812?TRACK=RSS [57] Lorenz K T, Edwards M J, Jankowski A F, et al. High pressure, quasi-isentropic compression experiments on the Omega laser[J]. High Energy Density Physics, 2006, 2(3/4):113-125. http://www.sciencedirect.com/science/article/pii/S1574181806000255 [58] Smith R F, Lorenz K T, Ho D, et al. Graded-density reservoirs for accessing high stress low temperature material states[J]. Astrophysics and Space Science, 2007, 307(1/2/3):269-272. doi: 10.1007/978-1-4020-6055-7_49 [59] Park H, Remington B A, Braun D, et al. Quasi-isentropic material property studies at extreme pressures: From Omega to NIF[J]. Journal of Physics: Conference Series, 2008, 112(4):042024. http://digital.library.unt.edu/ark:/67531/metadc898746/ [60] Yaakobi B, Boehly T R, Sangster T C, et al. Extended x-ray absorption fine structure measurements of quasi-isentropically compressed vanadium targets on the OMEGA laser[J]. Physics of Plasmas, 2008, 15(6):062703. doi: 10.1063/1.2938749 [61] Swift D C, Hawreliak J, El-Dasher B, et al. Flow stress of V, Mo, Ta, and W on nanosecond time scales[C]//Elert M, Furnish M D, Anderson W W, et al. Shock Compression of Condensed Matter 2009: Proceedings of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Nashville (Tennessee): the American Physical Society, 2009. [62] Park H S, Remington B A, Becker R C, et al. Viscous Rayleigh-Taylor instability experiments at high pressure and strain rate[J]. Physical Review Letters, 2010, 104(13):135504. http://europepmc.org/abstract/MED/21231088 [63] Park H S, Remington B A, Becker R C, et al. Strong stabilization of the Rayleigh-Taylor instability by material strength at megabar pressures[J]. Physics of Plasmas, 2010, 17(5):056314-9. doi: 10.1063/1.3363170 [64] Smith R F, Eggert J H, Saculla M D, et al. Ultrafast dynamic compression technique to study the kinetics of phase transformations in bismuth[J]. Physical Review Letters, 2008, 101(6):065701. doi: 10.1103/physrevlett.101.065701 [65] Prisbrey S T, Park H S, Remington B A, et al. Tailored ramp-loading via shock release of stepped-density reservoirs[J]. Physics of Plasmas, 2012, 19(5):056311. doi: 10.1063/1.3699361 [66] Brown J L, Alexander C S, Asay J R, et al. Extracting strength from high pressure ramp-release experiments[J]. Journal of Applied Physics, 2013, 114(22):223518. doi: 10.1063/1.4847535 [67] Brown J L, Alexander C S, Asay J R, et al. Flow strength of tantalum under ramp compression to 250 GPa[J]. Journal of Applied Physics, 2014, 115(4):043530. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6730879 [68] Vogler T J, Ao T, Asay J R. High-pressure strength of aluminum under quasi-isentropic loading[J]. International Journal of Plasticity, 2009, 25(4):671-694. http://www.sciencedirect.com/science/article/pii/S0749641908001782 [69] Kalantar D H, Chandler E A, Colvin J D, et al. Transient x-ray diffraction used to diagnose shock compressed Si crystals on the Nova laser[J]. Review of Scientific Instruments, 1999, 70(1):629-632. [70] Loveridge-Smith A, Allen A, Belak J, et al. Anomalous elastic response of silicon to uniaxial shock compression on nanosecond time scales[J]. Physical Review Letters, 2001, 86(11):2349-2352. http://www.ncbi.nlm.nih.gov/pubmed/11289926 [71] Kalantar D H, Allen A M, Gregori F, et al. Laser driven high pressure, high strain-rate materials experiments[C]//AIP Conference Proceedings: Shock Compression of Condensed Matter. Atlanta: the American Physical Society, 2002, 620(1): 615-618. [72] Kalantar D H, Belak J, Bringa E, et al. High-pressure, high-strain-rate lattice response of shocked materials[J]. Physics of Plasmas, 2003, 10(5):1569-1576. doi: 10.1063/1.1565118 [73] Hawreliak J, Colvin J D, Eggert J H, et al. Analysis of the x-ray diffraction signal for the α-ε transition in shock-compressed iron: Simulation and experiment[J]. Physical Review B, 2006, 74(18):184107. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PRBMDO000074000018184107000001&idtype=cvips&gifs=Yes [74] Hawreliak J A, Kalantar D H, Stölken J S, et al. High-pressure nanocrystalline structure of a shock-compressed single crystal of iron[J]. Physical Review B, 2008, 78(22):220101. http://adsabs.harvard.edu/abs/2008PhRvB..78v0101H [75] Rygg J R, Eggert J H, Lazicki A E, et al. Powder diffraction from solids in the terapascal regime[J]. Review of Scientific Instruments, 2012, 83(11):113904. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=6365144 [76] Higginbotham A, Patel S, Hawreliak J A, et al. Single photon energy dispersive x-ray diffraction[J]. Review of Scientific Instruments, 2014, 85(3):033906. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6778699 [77] Knudson M D, Desjarlais M P, Dolan D H. Shock-wave exploration of the high-pressure phases of carbon[J]. Science, 2008, 322(19):1822. http://meetings.aps.org/Meeting/SHOCK09/Event/105388 [78] Hicks D G, Boehly T R, Celliers P M, et al. High-precision measurements of the diamond Hugoniot in and above the melt region[J]. Physical Review B, 200, 78(17):174102. [79] Ping Y, Coppari F, Hicks D G, et al. Solid iron compressed up to 560 GPa[J]. Physical Review Letters, 2013, 111(6):065501. http://europepmc.org/abstract/med/23971582 [80] Mallozzi P J, Schwerzel R E, Epstein H M, et al. Fast extended-x-ray-absorption-fine-structure spectroscopy with a laser-produced x-ray pulse[J]. Physical Review A, 1981, 23(2):824-828. http://prola.aps.org/abstract/PRA/v23/i2/p824_1 [81] Meyerhofer D D, Yaakobi B, Marshall F J, et al. EXAFS detection of laser shock heating[J]. Bulletin of the American Physical Society (USA), 2001, 46(8):294. http://www.opticsinfobase.org/abstract.cfm?uri=HFSW-2001-WC2 [82] Yaakobi B, Marshall F J, Boehly T R, et al. Extended x-ray absorption fine-structure experiments with a laser-imploded target as a radiation source[J]. Journal of the Optical Society of America: B, 2003, 20(1):238-245. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=VIRT05000002000001000145000001&idtype=cvips&gifs=Yes [83] Yaakobi B, Meyerhofer D D, Boehly T R, et al. Extended x-ray absorption fine structure measurements of laser shocks in Ti and V and phase transformation in Ti[J]. Physics of Plasmas, 2004, 11(5):2688-2695. doi: 10.1063/1.1646673 [84] Yaakobi B, Meyerhofer D D, Boehly T R, et al. Dynamic EXAFS probing of laser-driven shock waves and crystal-phase transformations[J]. Physical Review Letters, 2004, 92(9):095504. http://www.opticsinfobase.org/abstract.cfm?uri=FiO-2004-FTuN4 [85] Yaakobi B, Boehly T R, Meyerhofer D D, et al. EXAFS measurement of iron bcc-to-hcp phase transformation in nanosecond-laser shocks[J]. Physical Review Letters, 2005, 95(7):075501. http://europepmc.org/abstract/MED/16196790 [86] Smith R F, Eggert J H, Swift D C, et al. Time-dependence of the alpha to epsilon phase transformation in iron[J]. Journal of Applied Physics, 2013, 114(22):223507. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=6708798 [87] Smith R F, Minich R W, Rudd R E, et al. Orientation and rate dependence in high strain-rate compression of single-crystal silicon[J]. Physical Review B, 2012, 86(24):245204. doi: 10.1103/PhysRevB.86.245204 [88] Smith R F, Eggert J H, Rudd R E, et al. High strain-rate plastic flow in Al and Fe[J]. Journal of Applied Physics, 2011, 110(12):123515. doi: 10.1063/1.3670001 [89] Coppari F, Smith R F, Eggert J H, et al. Experimental evidence for a phase transition in magnesium oxide at exoplanet pressures[J]. Nature Geoscience, 2013, 6(11):926-929. http://www.nature.com/ngeo/journal/v6/n11/abs/ngeo1948.html [90] Pang Wei-wei, Zhang Ping, Zhang Guang-cai, et al. Morphology and growth speed of hcp domains during shock-induced phase transition in iron[J]. Nature Scientific Reports, 2014, 4:03628. http://www.nature.com/articles/srep03628 [91] Yu Ji-dong, Wang Wen-jiang, Wu Qiang. Nucleation and growth in shock-induced phase transitions and how they determine wave profile features[J]. Physical Review Letters, 2012, 109(11):115701. http://europepmc.org/abstract/MED/23005645 [92] Smith R F, Minich R W, Rudd R E, et al. Orientation and rate dependence in high strain-rate compression of single-crystal silicon[J]. Physical Review B, 2012, 86(24):245204. doi: 10.1103/PhysRevB.86.245204 [93] Jensen B J, Rigg P A, Knudson M D, et al. Dynamic compression of iron single crystals[C]//Furnish M D, Elert M, Russell T P, et al. Shock Compression of Condensed Matter-2005: Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter. Baltimore, Maryland (USA): American Institute of Physics, 2006, 845(1): 232-235. 期刊类型引用(4)
1. 李牧，张红平，陈实，陶沛东，祝航，周沧涛，赵剑衡，孙承纬. 激光驱动材料动态压缩技术. 强激光与粒子束. 2022(01): 5-28 . 
百度学术2. 康冬冬，曾启昱，张珅，王小伟，戴佳钰. 激光产生温稠密物质的微观动力学过程及状态诊断. 强激光与粒子束. 2020(09): 82-96 . 百度学术3. 罗斌强，张红平，赵剑衡，孙承纬. 斜波压缩实验数据的正向Lagrange处理方法研究. 爆炸与冲击. 2017(02): 243-248 . 
本站查看4. 罗斌强，张红平，种涛，王桂吉，谭福利，赵剑衡，孙承纬. 磁驱动斜波压缩实验结果的不确定度分析. 高压物理学报. 2017(03): 295-300 . 百度学术其他类型引用(3)
-
下载:
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
下载:
百度学术
图(9)
计量
- 文章访问数: 3265
- HTML全文浏览量: 332
- PDF下载量: 685
- 被引次数: 7