基于夏比冲击试验的材料失效模型参数

徐小东; 李华良; 张涛

doi:10.11883/1001-1455(2016)01-0057-07

基于夏比冲击试验的材料失效模型参数

doi: 10.11883/1001-1455(2016)01-0057-07

1.
华中科技大学船舶与海洋工程学院，湖北武汉 430074
2.
中国船舶重工集团公司第七一九研究所，湖北武汉 430064

基金项目:

国家自然科学基金项目 10702022

华中科技大学青年教师基金项目 0114140034

详细信息

作者简介:
徐小东(1990-)，男，硕士

通讯作者:
张涛, zhangt7666@hust.edu.cn

中图分类号: O346.1
计量
- 文章访问数: 4578
- HTML全文浏览量: 1241
- PDF下载量: 362
- 被引次数: 0
出版历程
- 收稿日期: 2014-07-18
- 修回日期: 2015-04-30
- 刊出日期: 2016-01-25

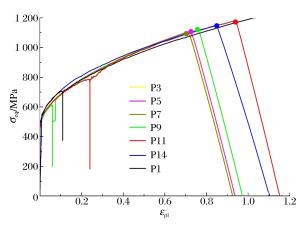
Parameters for the material failure model based on Charpy impact test

1.
School of Naval Architecture and Ocean Engineering, Huazhong University ofScience & Technology, Wuhan 430074, Hubei, China
2.
No.719 Research Institute of China Shipbuilding Industry Corporation, Wuhan 430064, Hubei, China

摘要

摘要: 结合夏比冲击试验和ABAQUS显式动力数值模拟，对Q370d钢进行了Johnson-Cook失效模型参数研究。首先，在不考虑材料失效的情况下，通过3种不同厚度的无缺口试件冲击实验对有限元模型参数设置和材料本构模型的准确性进行了验证，同时还讨论了试件断裂区网格的合适尺寸；在此基础上，基于正交设计，通过大量的有限元数值模拟得到失效模型参数样本，利用回归分析求得冲击功与失效模型参数的回归方程组；最后结合夏比V型缺口冲击试验，求解Q370d钢的失效模型参数，并对断裂截面的力学特性进行了分析，可为工程应用提供参考。
- 固体力学 /
- Johnson-Cook失效模型参数 /
- 夏比冲击试验 /
- Q370d钢 /
- 正交设计 /
- 回归分析
Abstract: This paper aims to obtain the parameters for the failure model based on the Charpy impact test, which has been widely used to study dynamic fracture properties of metallic materials. Based on the explicit dynamic finite element method in ABAQUS, FEM model of Charpy impact test was conducted. We began by discussing the accuracy of the parameters of JC constitutive model and the grid size of the fracture section of V-notch specimen. Then, based on the orthogonal design method, we designed a set of parameters for JC failure model and obtained using finite element calculation the samples of the parameters and impact energy. Next, we obtained the regression equations containing the parameters and impact energy by regression analysis and finally, by solving these regression equations, we achieved the comparatively accurate parameters for JC failure model for Q370d steel. These parameters will be useful for engineering applications and our method will be a valuable way to obtain parameters for other kinds of materials, especially without necessarily meeting the conditions of performing some tests.
- solid mechanics /
- parameter of JC failure model /
- Charpy impact test /
- Q370d steel /
- orthogonal design method /
- regression analysis

HTML全文

图 1 夏比冲击试验V型缺口试件的几何、网格图

Figure 1. Geometry and grid for Charpy V-notch test specimen

下载: 全尺寸图片幻灯片

图 2 标准试件的最终变形

Figure 2. Final deformation of the standard specimens

下载: 全尺寸图片幻灯片

图 3 材料破坏的典型应力应变曲线

Figure 3. Typical stress-strain curvesduring the material damage progress

下载: 全尺寸图片幻灯片

图 4 V型缺口试件的最终变形

Figure 4. Final deformation of V-notch specimens

下载: 全尺寸图片幻灯片

图 5 实验冲头力

Figure 5. Experimental punch loads

下载: 全尺寸图片幻灯片

图 6 计算和实验的冲头力

Figure 6. Computed and experimental punch loads

下载: 全尺寸图片幻灯片

图 7 V型缺口试件计算的最终变形及观测点

Figure 7. Computed final deformation of V-notch specimensand location of observation points

下载: 全尺寸图片幻灯片

图 8 观测点的等效塑性应变与等效应力曲线

Figure 8. Curves of equivalent stress vsequivalent plastic strain at observation points

下载: 全尺寸图片幻灯片

图 9 试件断裂截面上单元应力三轴度曲线

Figure 9. Stress triaxiality curves of observation elements at the fracture cross-sections of specimens

下载: 全尺寸图片幻灯片

表 1 标准试件的实验和数值模拟结果

Table 1. Experimental and simulated results of the standard specimens

W/mm	A_{k, exp}/J	A_{k, num}/J	ε_{A_k}/%	d_{t, exp}/mm	d_{t, num}/mm	ε_{d_t}/%	d_{c, exp}/mm	d_{c, num}/mm	ε_{d_c}/%	l_exp/mm	l_num/mm	ε_l/%
4	181.7	180.3	-0.8	6.86	7.26	5.8	2.52	2.69	6.7	24.93	23.89	-4.2
5	226.6	224.7	-0.8	8.17	8.71	6.6	3.22	3.39	5.3	25.37	24.04	-5.5
6	277.8	270.6	-2.6	9.40	9.94	5.7	3.91	4.09	4.6	25.33	23.87	-6.1

下载: 导出CSV

表 2 不同断裂区网格尺寸下的冲击功、摆锤冲击力

Table 2. Impact energy and pendulum forcein plane models with different mesh sizes

Δd/mm	A_k1/J	A_k2/j	F_m/kN
0.300	14.69	9.45	0.417
0.200	14.69	8.12	0.334
0.100	14.78	7.14	0.277
0.075	14.81	7.36	0.291
0.050	14.81	6.99	0.275

下载: 导出CSV

表 3 JC失效模型的正交设计试验表

Table 3. Orthogonal design parameters for JC failure model

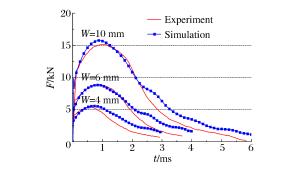
No.	D₁	D₂	D₃	A_k/J
No.	D₁	D₂	D₃	W=10 mm	W=6 mm	W=4 mm
1	0.15	3	-1.8	151.57	89.04	57.61
2	0.15	4	-2.2	130.82	79.83	53.25
3	0.15	5	-2.6	113.26	67.86	46.08
4	0.15	6	-3.0	95.71	56.69	38.84
5	0.15	7	-3.4	81.50	47.67	32.54
6	0.20	3	-2.6	97.34	56.13	44.43
7	0.20	4	-3.0	92.88	54.81	34.06
8	0.20	5	-3.4	91.53	48.69	33.76
9	0.20	6	-1.8	287.76	185.80	107.57
10	0.20	7	-2.2	253.14	160.20	100.67
11	0.25	3	-3.4	87.83	48.38	31.22
12	0.25	4	-1.8	232.39	137.77	84.92
13	0.25	5	-2.2	203.56	122.17	77.73
14	0.25	6	-2.6	169.53	103.94	67.87
15	0.25	7	-3.0	150.13	87.96	57.72
16	0.30	3	-2.2	160.57	91.74	57.25
17	0.30	4	-2.6	152.92	87.35	54.97
18	0.30	5	-3.0	141.67	80.70	50.92
19	0.30	6	-3.4	129.61	73.81	46.59
20	0.30	7	-1.8	288.63	193.92	114.43
21	0.35	3	-3.0	130.85	73.26	44.74
22	0.35	4	-3.4	128.04	71.75	43.96
23	0.35	5	-1.8	286.80	179.69	103.27
24	0.35	6	-2.2	268.54	162.92	98.42
25	0.35	7	-2.6	230.74	138.54	87.47

下载: 导出CSV

参考文献(17)

[1]	朱建士, 胡晓棉, 王裴, 等.爆炸与冲击动力学若干问题研究进展[J].力学进展, 2010, 40(4):401-423. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lxjz201004003 Zhu Jianshi, Hu Xiaomian, Wang Pei, et al. A review on research progress in explosion mechanics and impact dynamics[J]. Advances in Mechanics, 2010, 40(4):401-423. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=lxjz201004003
[2]	Jiang F C, Vecchio K S. Hopkinson bar loaded fracture experimental technique: A critical review of dynamic fracture toughness tests[J]. Applied Mechanics Reviews, 2009, 62:(6):1-39. doi: 10.1115-1.3124647/
[3]	李玉龙, 郭伟国, 徐绯, 等.Hopkinson压杆技术的推广应用[J].爆炸与冲击, 2006, 26(5):385-394. doi: 10.3321/j.issn:1001-1455.2006.05.001 Li Yulong, Guo Weiguo, Xu Fei, et al. The extended application of Hopkinson bar technique[J]. Explosion and Shock Waves, 2006, 26(5):385-394. doi: 10.3321/j.issn:1001-1455.2006.05.001
[4]	Rossoll A, Berdin C, Forget P, et al. Mechanical aspects of the Charpy impact test[J]. Nuclear Engineering and Design, 1999, 188(2):217-229. http://cn.bing.com/academic/profile?id=b3cf912407bc75b1d3089923033aa981&encoded=0&v=paper_preview&mkt=zh-cn
[5]	潘建华, 陈学东, 韩豫.-196℃奥氏体不锈钢母材与焊缝的动态断裂韧性[J].爆炸与冲击, 2013, 33(4):381-386. doi: 10.3969/j.issn.1001-1455.2013.04.008 Pan Jianhua, Chen Xuedong, Han Yu. Dynamic fracture toughness of S30408 austenitic stainless steel base and weld metals at -196 ℃[J]. Explosion and Shock Waves, 2013, 33(4):381-386. doi: 10.3969/j.issn.1001-1455.2013.04.008
[6]	Du J, Strangwood M, Davis C L. Effect of tin particles and grain size on the charpy impact transition temperature in steels[J]. Journal of Material Science & Technology, 2012, 28(10):878-888. http://cn.bing.com/academic/profile?id=226f88bcf1b307eb55ffe81ab423ec76&encoded=0&v=paper_preview&mkt=zh-cn
[7]	Bao Y B. Prediction of ductile crack formation in uncracked bodies[D]. MIT, 2003.
[8]	Zheng L. Fracture of welded aluminum thin-walled structure[D]. MIT, 2005.
[9]	Lee Y W. Fracture prediction in metal sheets[D]. MIT, 2005.
[10]	Luo M, Wierzbicki T. Numerical failure analysis of a stretch-bending test on dual-phase steels using a phenomenologicla fracture model[J]. International Journal of Solids and Structures, 2010, 47(22/23):3084-3102. http://dspace.mit.edu/bitstream/handle/1721.1/96040/Luo-2010-Numerical%20failure%20an.pdf;sequence=1
[11]	Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures, and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1):31-48. doi: 10.1016-0013-7944(85)90052-9/
[12]	陈刚, 陈忠富, 徐伟芳, 等.45钢的JC损伤失效参量研究[J].爆炸与冲击, 2007, 27(2):131-135. doi: 10.3321/j.issn:1001-1455.2007.02.007 Chen Gang, Chen Zhongfu, Xu Weifang, et al. Investigation on the J-C ductile fracture parameters of 45 steel[J]. Explosion and Shock Waves, 2007, 27(2):131-135. doi: 10.3321/j.issn:1001-1455.2007.02.007
[13]	张伟, 肖新科, 魏刚.7A04铝合金的本构关系和失效模型[J].爆炸与冲击, 2011, 31(1):81-87. doi: 10.11883/1001-1455(2011)01-0081-07 Zhang Wei, Xiao Xinke, Wei Gang. Constitutive relation and fracture model of 7A04 aluminum alloy[J]. Explosion and Shock Waves, 2011, 31(1):81-87. doi: 10.11883/1001-1455(2011)01-0081-07
[14]	王磊, 高彩茹, 王彦锋, 等.我国桥梁钢的发展历程及展望[J].机械工程材料, 2008, 32(5):1-3. doi: 10.3969/j.issn.1000-3738.2008.05.001 Wang Lei, Gao Cairu, Wang Yanfeng, et al. Development of bridge steels in China[J]. Materials for Mechanical Engineering, 2008, 32(5):1-3. doi: 10.3969/j.issn.1000-3738.2008.05.001
[15]	GB/T 229-2005金属夏比缺口冲击试验方法[S].
[16]	于文静, 史健勇, 赵金城.Q345钢材动态力学性能研究[J].建筑结构, 2011, 41(3):28-30. doi: 10.1017-S0963180108080353/ Yu Wenjing, Shi Jianyong, Zhao Jincheng. Research of dynamic mechanical behavior of Q345 steel[J]. Building Structure, 2011, 41(3):28-30. doi: 10.1017-S0963180108080353/
[17]	Yu H L, Jeong D Y. Application of a stress triaxiality dependent fracture criterion in the finite element analysis of unnotched Charpy specimens[J]. Theoretical and Applied Fracture Mechanics, 2010, 54(1): 54-62. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=01fd53c23aa512891d083b81e8a85581