Model experiment to study cumulative damage effects of young shotcrete under blasting load
-
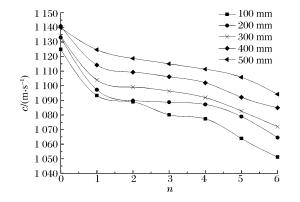
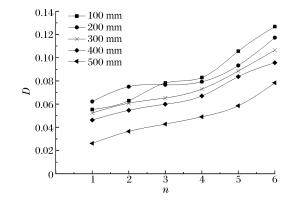
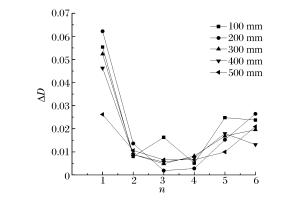
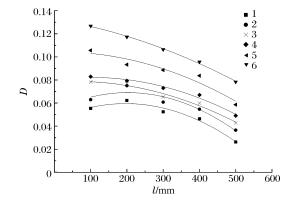
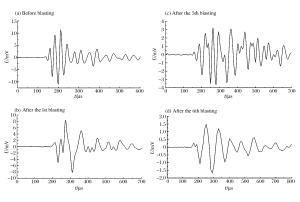
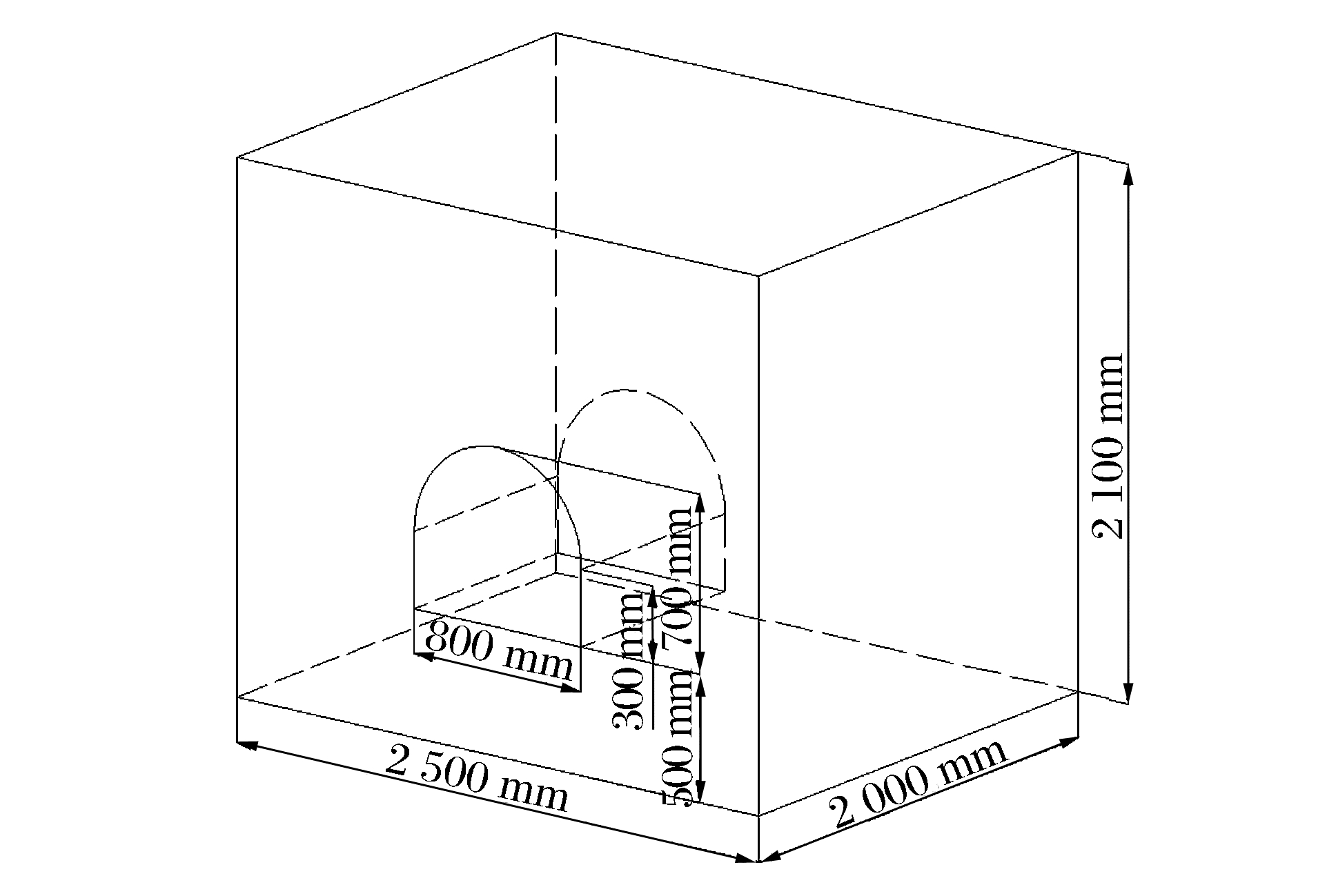
摘要: 利用模型实验的手段模拟了巷道的爆破掘进，并在实验中辅以声波测试，通过分析声波波速和声波波形的变化规律，研究了新喷射混凝土在多次爆破动载作用下的累积损伤效应。实验结果表明，爆破次数、与掌子面之间的距离和爆破药量均会影响喷射混凝土的累积损伤，这种影响体现在声波波速和波形2个方面：爆破次数增加、距离减小和药量增加，则声速降低值越大，波形变化越明显，即累积损伤值越大；爆破次数和距掌子面的距离均与累积损伤呈非线性关系，其中距离与爆破损伤之间的非线性关系可以用二次多项式进行较好的拟合；第一次爆破对声速和波形影响最大，造成的单次损伤值也最大；在小药量爆破的情况下，测试面的最大累积损伤值达到了0.1268，表明爆破近区喷射混凝土的损伤是需要关注的重点。Abstract: In this work we simulated the blasting excavation in a mine tunnel using a model test. Adopting the sound wave test method, we investigated the cumulative damage effects of young shotcrete under multiple blasting loads by analyzing variations of acoustic velocity and acoustic waveform during the model test. The results indicate that all the following factors, the times of blasting, the distance between the tunnel face and the test plane, and the dosage of the explosive used as are responsible for the cumulative damage of shotcrete. Their influences are shown both in the acoustic velocity and the acoustic waveform: the more times of blasting, the shorter distance, and the greater explosive dosage, then the greater the reduction value of the acoustic velocity and the more obvious the change of the acoustic waveform, and the greater the cumulative damage value. Specifically, there is a nonlinear relationship between the times of blasting and the cumulative damage. Between the distance and the cumulative damage there also exists a nonlinear relationship, which can be well fitted by a quadratic polynomial. Furthermore, it is found that the first time of blasting affects the acoustic velocity and the acoustic waveform the most, and causes the greatest damage. In general, when the explosive dosage is small, the maximum cumulative damage reaches 0.1268, which indicates that the shotcrete damage close to the blasting area should be the major concern.
-
Key words:
- mechanics of explosion /
- cumulative damage /
- model test /
- young shotcrete /
- sound wave test /
- blasting load
-
图 3 喷射混凝土爆破累积损伤曲线
Figure 3. Damage accumulation curves of shotcrete under blasting load
图 5 累积损伤随距离变化的拟合曲线
Figure 5. Fitted curves of damage accumulation varying with distance
表 1 Ⅲ类围岩及模型材料力学参数
Table 1. Mechanical parameters of type Ⅲ surrounding rock and model materials
介质 γ/(kN·m-3) E/GPa ν σp/MPa cL/(km·s-1) Ⅲ类围岩 24.50~26.54 6~20 0.25~0.30 20~60 3~4.5 模型材料 18.85~20.42 0.77~2.56 0.25~0.30 2.56~7.69 1.22~1.84 实测值 19.6 2.49 0.29 7.8 1.61 
下载: 导出CSV
表 2 主要参数的相似比例系数
Table 2. Proportional coefficient of main parameters
序号 对应物理参量 相似准则 相似比 1 线尺寸(L) CL 6 2 质量密度(ρ) Cρ 1.3 3 加速度(a) Ca 1 4 弹性模量(E) CE=CLCρCa 7.8 5 单轴抗压强度(σ) Cσ=CE 7.8 6 炸药药量(q) Cq=CρCL3 280.8 7 炸药爆速(v) Cv=CE0.5Cρ-0.5 1 8 应力(σ) Cσ=CE 7.8 9 时间(t) Ct=CL0.5 2.45
下载: 导出CSV
表 3 回归拟合系数
Table 3. Regressive fitted coefficient
爆破次数 A B1/mm-1 B2/mm-2 R2 1 0.0457 1.4×10-4 -3.6×10-7 0.9716 2 0.0537 1.5×10-4 -3.8×10-7 0.9210 3 0.0782 2.0×10-5 -1.8×10-7 0.9802 4 0.0801 4.1×10-5 -2.0×10-7 0.9836 5 0.1041 7.0×10-6 -1.8×10-7 0.9337 6 0.1327 -5.2×10-5 -1.1×10-7 0.9972
下载: 导出CSV
-
[1] 程良奎.喷射混凝土[M].北京:中国建筑工业出版社, 1990. [2] Grady D E, Kipp M E. Continuum modeling of explosive fracture in oil shale[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1980, 17(3):147-157. [3] Liu L, Katsabanis P D. Development of a continuum damage model for blasting analysis[J]. International Journal of Rock Mechanics & Mining Sciences, 1997, 34(2):217-231. http://cn.bing.com/academic/profile?id=3719d16e77f23d86f560aa6532cc0da2&encoded=0&v=paper_preview&mkt=zh-cn [4] 杨军, 王树仁.岩石爆破分形损伤模型研究[J].爆炸与冲击, 1996, 16(1):5-10. http://www.bzycj.cn/article/id/10492Yang Jun, Wang Shuren. Study on fractal damage model of rock fragmentation by blasting[J]. Explosion and Shock Waves, 1996, 16(1):5-10. http://www.bzycj.cn/article/id/10492 [5] 颜峰, 姜福兴.爆炸冲击荷载作用下岩石的损伤实验[J].爆炸与冲击, 2009, 29(3):275-280. doi: 10.3321/j.issn:1001-1455.2009.03.009Yan Feng, Jiang Fuxing. Experiment on rock damage under blasting load[J]. Explosion and Shock Waves, 2009, 29(3):275-280. doi: 10.3321/j.issn:1001-1455.2009.03.009 [6] 费鸿禄, 杨卫风, 张国辉, 等.金属矿山矿柱回采时爆破荷载下采空区的围岩稳定性[J].爆炸与冲击, 2013, 33(4):344-350. doi: 10.3969/j.issn.1001-1455.2013.04.002Fei Honglu, Yang Weifeng, Zhang Guohui, et al. Surrounding rock stability of mined-out area under blast loading in metal mine pillar robbing[J]. Explosion and Shock Waves, 2013, 33(4):344-350. doi: 10.3969/j.issn.1001-1455.2013.04.002 [7] 孟凡兵, 林从谋, 蔡丽光, 等.小净距隧道爆破开挖中夹岩累积损伤计算方法及其应用[J].岩土力学, 2011, 32(5):1491-1494. doi: 10.3969/j.issn.1000-7598.2011.05.032Meng Fanbing, Lin Congmou, Cai Liguang, et al. Cumulative damage evaluation of clip rock in small-distance tunnels caused by blasting excavation and its application[J]. Rock and Soil Mechanics, 2011, 32(5):1491-1494. doi: 10.3969/j.issn.1000-7598.2011.05.032 [8] 胡振锋, 吴子燕, 李政.喷射混凝土衬砌爆破损伤的数值分析[J].矿业研究与开发, 2005, 25(5):71-75. doi: 10.3969/j.issn.1005-2763.2005.05.024Hu Zhenfeng, Wu Ziyan, Li Zheng. Numerical analysis on the blasting damage of shotcrete lining[J]. Mining Research and Development, 2005, 25(5):71-75. doi: 10.3969/j.issn.1005-2763.2005.05.024 [9] 丁泰山, 李万喜.爆破施工对新喷射混凝土的损伤影响分析[J].地下空间与工程学报, 2006, 2(5):834-838. http://d.old.wanfangdata.com.cn/Periodical/dxkj200605030Ding Taishan, Li Wanxi. Damage analysis of fresh shotcrete under excavating blast load[J]. Chinese Journal of Underground Space and Engineering, 2006, 2(5):834-838. http://d.old.wanfangdata.com.cn/Periodical/dxkj200605030 [10] 谢江峰, 李夕兵, 宫凤强, 等.隧道爆破震动对新喷混凝土的累积损伤计算[J].中国安全科学学报, 2012, 22(6):118-123. doi: 10.3969/j.issn.1003-3033.2012.06.019Xie Jiangfeng, Li Xibing, Gong Fengqiang, et al. Cumulative damage evaluation of young shotcrete in tunnel caused by blast-induced vibration[J]. China Safety Science Journal, 2012, 22(6):118-123. doi: 10.3969/j.issn.1003-3033.2012.06.019 [11] 徐挺.相似理论与模型试验[M].北京:中国农业机械出版社, 1982. [12] 单仁亮, 周纪军, 夏宇, 等.粘结式锚杆在爆炸动载下轴向应力分布研究[J].岩土力学, 2011, 32(10):2965-2971. doi: 10.3969/j.issn.1000-7598.2011.10.012Shan Renliang, Zhou Jijun, Xia Yu, et al. Axial stress distribution of grouted rockbolts subjected to blast loading[J]. Rock and Soil Mechanics, 2011, 32(10):2965-2971. doi: 10.3969/j.issn.1000-7598.2011.10.012 [13] 中华人民共和国国家质量监督检验检疫总局.GB50086-2001, 中华人民共和国建设部.锚杆喷射混凝土支护技术规范[S].北京: 中国计划出版社, 2001. [14] 郝松林, 陈铸曾.损伤及损伤力学[J].国防科技大学学报, 1984, 6(3):1-36. http://d.old.wanfangdata.com.cn/Periodical/hkxb200002006Hao Songlin, Chen Zhuzeng. Damage and damage mechanics[J]. Journal of National University of Defense Technology, 1984, 6(3):1-36. http://d.old.wanfangdata.com.cn/Periodical/hkxb200002006 [15] 朱传云, 喻胜春.爆破引起岩体损伤的判别方法研究[J].工程爆破, 2001, 7(1):12-16. doi: 10.3969/j.issn.1006-7051.2001.01.003Zhu Chuanyun, Yu Shengchun. Study on the criterion of rockmass damage caused by blasting[J]. Engineering Blasting, 2001, 7(1):12-16. doi: 10.3969/j.issn.1006-7051.2001.01.003 -
点击查看大图
图(6) / 表(3)
计量
- 文章访问数: 4335
- HTML全文浏览量: 1187
- PDF下载量: 661
- 被引次数: 0