A model for rigid sharp-nosed projectile perforating metallic targets considering free-surface and cracking effects
-
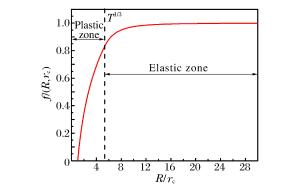
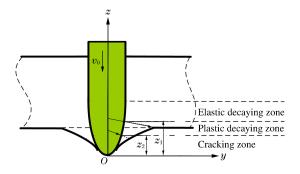
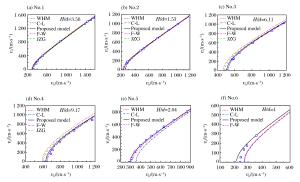
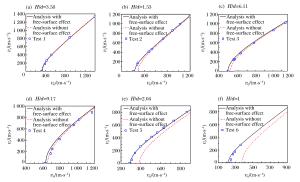
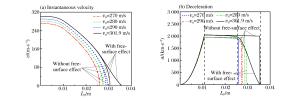
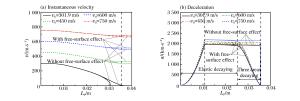
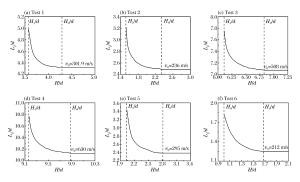
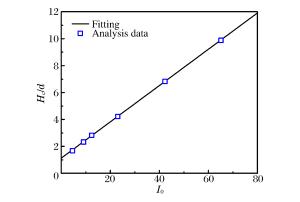
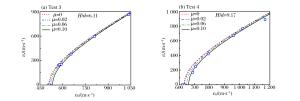
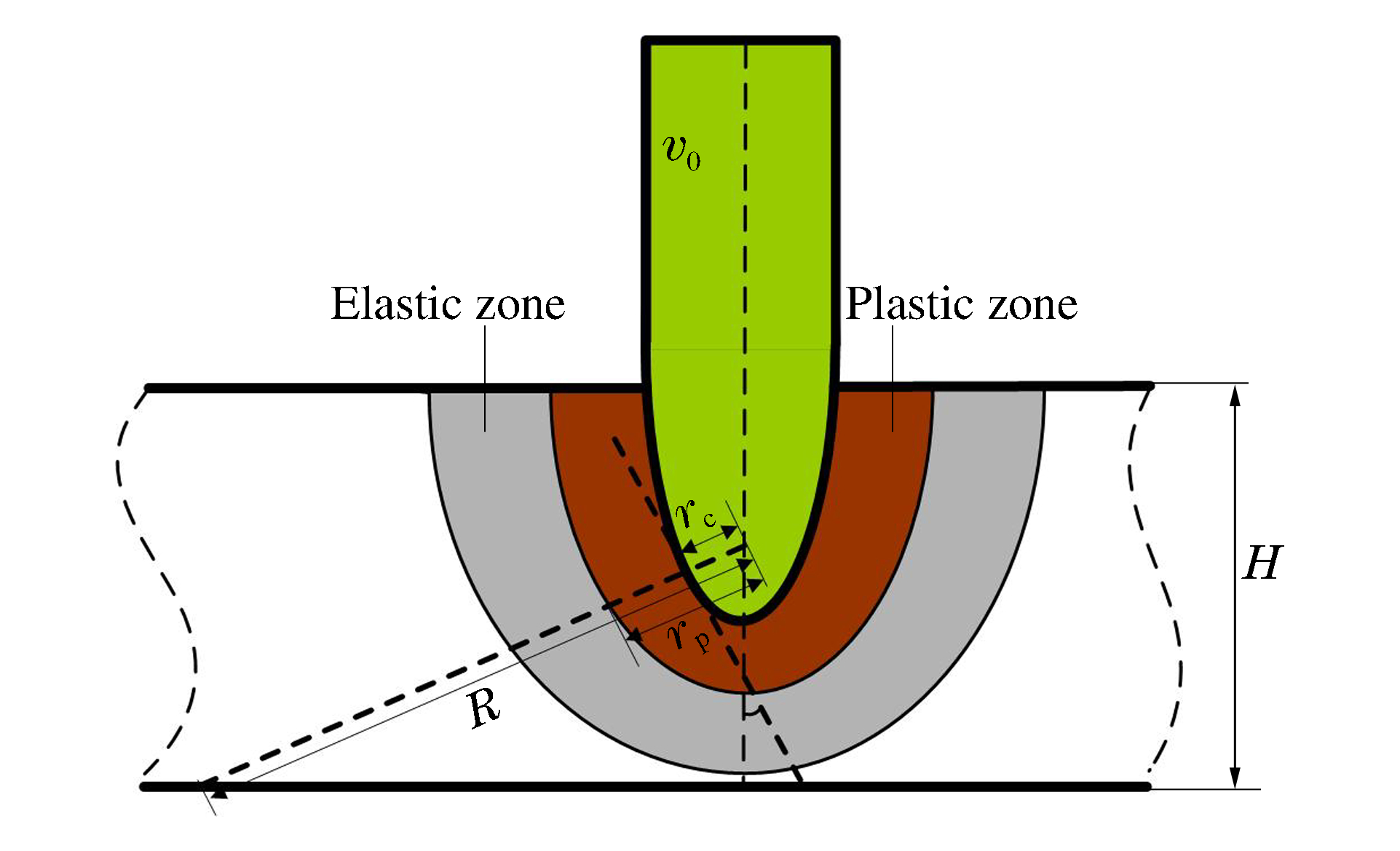
摘要: 将靶体视为不可压缩材料，假定空腔膨胀产生塑性-弹性响应分区，构造了靶背自由表面效应的衰减函数。将衰减函数乘以可压缩幂次硬化材料的阻力方程，得到了弹体贯穿金属靶板的阻力函数。基于弹性衰减-塑性衰减-开裂3个阶段，建立了同时考虑靶体可压缩性、靶背自由表面和开裂影响的弹体贯穿有限厚金属靶板的分析模型，推导得出了弹体瞬时速度的解析方程，并采用数值方法计算得到了弹体的过载、瞬时速度和残余速度。通过与6组实验数据和已有模型的对比得到，当靶板厚度和弹体冲击速度在一定范围内时，需要考虑自由表面效应的影响。Abstract: Treating the target as the incompressible material, by assuming that the cavity expansion produce plastic-elastic response region, the decay function for the back free-surface effect of target is constructed. The forcing function of metallic targets for perforation is obtained by multiplying the forcing function of compressible Strain-Harding targets with the decay function. Based on the three stage of elastic-decaying, plastic-decaying and cracking, the analytical model considering the compressibility, the back free-surface effect of target and cracking is established, and the analytical equation of instantaneous velocity of projectile is deduced. The deceleration, instantaneous and residual velocity of projectile is calculated by numerical methods. Through comparison with six sets of experimental data and other existing models, with the target thickness and impact velocity in a certain range, the free-effect should be considered.
-
图 1 弹体冲击靶板过程中的弹塑性响应
Figure 1. Elastic-plastic responses during projectile striking target
图 4 本文模型剩余速度预测曲线与实验数据的对比
Figure 4. Comparison of residual velocities between proposed model and experimental data
图 5 本文模型剩余速度预测曲线与已有模型及实验数据的比较
Figure 5. Comparison of predictions of residual velocities between the model of this paper and other models
图 6 自由表面效应对6组贯穿实验残余速度预测的影响
Figure 6. Free-surface effect on the prediction of residual velocities for six sets of experimental data
图 7 侵彻情形下冲击速度对自由表面效应的影响
Figure 7. Influence of impact velocity on free-surface effect while the projectile penetrating into the target
图 8 贯穿情形下冲击速度对自由表面效应的影响
Figure 8. Influence of impact velocity on free-surface effect while the projectile penetrating through the target
图 10 半无限临界靶板厚度与冲击因子关系
Figure 10. Semi-infinite critical plate thickness vs. impact factor
图 11 不同摩擦因数下弹体初始速度与残余速度
Figure 11. Residual velocities vs. initial velocities at different friction coefficient
表 1 刚性弹贯穿金属靶板实验的弹体参数
Table 1. Experimental projectile parameters in perforation of rigid projectiles into metallic targets
下载: 导出CSV
表 2 刚性弹贯穿金属靶板实验的靶体参数
Table 2. Experimental target parameters in perforation of rigid projectiles into metallic targets
No. 文献 弹头形状 靶体材料 H/mm E/GPa ρ/(g·cm-3) Y/MPa γ n 1 [13] 锥头弹 6061-T6铝 25.4 68.9 2.71 276 0.33 0.051 2 [15] 锥头弹 5083-H131铝 12.7 70.3 2.66 276 1/3 0.084 3 [15] 锥头弹 5083-H131铝 50.8 70.3 2.66 276 1/3 0.084 4 [15] 锥头弹 5083-H131铝 76.2 70.3 2.66 276 1/3 0.084 5 [16] 卵头弹 6061-T651铝 26.3 69 2.71 262 0.33 0.085 6 [17] 卵头弹 5083-H116铝 20 71 2.66 240 0.33 0.108
下载: 导出CSV
-
[1] 陈小伟.穿甲/侵彻问题的若干工程研究进展[J].力学进展, 2009, 39(3):316-351. doi: 10.3321/j.issn:1000-0992.2009.03.006Chen Xiaowei. Advances in the penetration/perforation of rigid projectiles[J]. Advances in Mechanics, 2009, 39(3):316-351. doi: 10.3321/j.issn:1000-0992.2009.03.006 [2] 肖云凯, 吴昊, 方秦, 等.穿甲弹冲击多层金属靶板终点弹道参数的研究进展[J].防护工程, 2014, 36(3):52-68. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fhgc201403010Xiao Yunkai, Wu Hao, Fang Qin, et al. Review on the terminal ballistic parameters of the armor-piercing penetrator striking the multi-layered metallic shields[J]. Projective engineering, 2014, 36(3):52-68. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=fhgc201403010 [3] 蒋志刚, 曾首义, 周建平.尖头弹丸撞击下金属靶板弹道极限的两种工程模型[J].应用力学学报, 2005, 22(1):21-25. doi: 10.3969/j.issn.1000-4939.2005.01.005Jiang Zhigang, Zeng Shouyi, Zhou Jianping. The two engineering models of ballistic limits for sharp-nosed projectile striking metallic plates[J]. Chinese Journal of Applied Mechanics, 2005, 22(1):21-25. doi: 10.3969/j.issn.1000-4939.2005.01.005 [4] Forrestal M J, Warren T L. Perforation equations for conical and ogive nose rigid projectiles into aluminum target plates[J]. International Journal of Impact Engineering, 2009, 36(2):220-225. doi: 10.1016/j.ijimpeng.2008.04.005 [5] Chen Xiaowei, Li Qingming. Perforation of a thick plate by rigid projectiles[J]. International Journal of Impact Engineering, 2003, 28(7):743-759. doi: 10.1016/S0734-743X(02)00152-5 [6] Wen Heming. Predicting the penetration and perforation of targets by projectiles at normal incidence[J]. Mechanics of Structures and Machines, 2002, 30(4):543-577. doi: 10.1081/SME-120015076 [7] 吴乔国.不同材料靶板的抗弹性能研究[D].合肥: 中国科学技术大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10358-1012503653.htm [8] 孙炜海.锥头弹丸正撞击下金属靶板破坏模式的理论和数值模拟研究[D].合肥: 中国科学技术大学, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1498383 [9] 蒋志刚, 曾首义, 周建平.中等厚度金属靶板的三阶段贯穿模型[J].兵工学报, 2007, 28(9):1046-1052. doi: 10.3321/j.issn:1000-1093.2007.09.005Jiang Zhigang, Zeng Shouyi, Zhou Jianping. A three-stage model for the perforation of moderately thick metallic plates[J]. Acta Armamentarii, 2007, 28(9):1046-1052. doi: 10.3321/j.issn:1000-1093.2007.09.005 [10] Luk V K, Forrestal M J, Amos D E. Dynamic spherical cavity expansion of strain-hardening materials[J]. Journal of Applied Mechanics, 1991, 58(1):1-6. doi: 10.1115/1.2897150 [11] Warren T L, Poormon K L. Penetration of 6061-T6511 aluminum targets by ogive-nosed VAR 4340 steel projectiles at oblique angles: Experiments and simulations[J]. International Journal of Impact Engineering, 2001, 25(10):993-1022. doi: 10.1016/S0734-743X(01)00024-0 [12] 孔祥振, 方秦, 吴昊.考虑靶体自由表面和开裂区影响的可变形弹体侵彻脆性材料的终点弹道分析[J].兵工学报, 2014, 35(6):814-821. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bgxb201406010Kong Xiangzhen, Fang Qin, Wu Hao. Ballistics study of the deformable projectile penetrating brittle material targets with the free-surface and crack region effects[J]. Acta Armamentarii, 2014, 35(6):814-821. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bgxb201406010 [13] Rosenberg Z, Forrestal M J. Perforation of aluminum plates with conical-nosed rods-additional data and discussion[J]. Journal of Applied Mechanics, 1988, 55(1):236-238. doi: 10.1115/1.3173639 [14] Wen Heming. Deformation and t earing of clamped work-hardening beams subjected impulsive loading[J]. International Journal of Impact Engineering, 1996, 18(4):425- 433. doi: 10.1016/0734-743X(95)00053-D [15] Forrestal M J, Luk V K, Brar N S. Perforation of aluminum armor plates with conical-nose projectiles[J]. Mechanics of Materials, 1990, 10(1):97-105. doi: 10.1016-0167-6636(90)90020-G/ [16] Piekutowski A J, Forrestal M J, Poormon K L, et al. Perforation of aluminum plates with ogive-nose steel rods at normal and oblique impacts[J]. International Journal of Impact Engineering, 1996, 18(7):877-887. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=416180fc47231590075ba96a78c39250 [17] Børvik T, Forrestal M J, Warren T L. Perforation of 5083-H116 aluminum armor plates with ogive-nose rods and 7.62 mm APM2 bullets[J]. Experimental Mechanics, 2010, 50(7):969-978. doi: 10.1007/s11340-009-9262-5 [18] Forrestal M J, Brar N S, Luk V K. Penetration of strain-hardening targets with rigid spherical-nose rods[J]. Journal of Applied Mechanics, 1991, 58(1):7-10. doi: 10.1115/1.2897183 [19] 周辉.弹塑性材料中的空穴膨胀理论及其在侵彻力学中的应用[D].合肥: 中国科学技术大学, 2004. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y615875 [20] Tucker M T, Horstemeyer M F, Whittington W R, et al. The effect of varying strain rates and stress states on the plasticity, damage, and fracture of aluminum alloys[J]. Mechanics of Materials, 2010, 42(10):895-907. doi: 10.1016/j.mechmat.2010.07.003 [21] 肖云凯, 方秦, 吴昊, 等.刚性尖头弹扩孔贯穿金属靶板理论模型的讨论[J].振动与冲击, 2016, 35(1):195-215. http://d.old.wanfangdata.com.cn/Periodical/zdycj201601031Xiao Yunkai, Fang Qin, Wu Hao, et al. Discussions on the ductile hole expansion perforation models for the rigid sharp-nosed projectile perforating metallic plate[J].Journal of Vibration and Shock, 2016, 35(1):195-215. http://d.old.wanfangdata.com.cn/Periodical/zdycj201601031 [22] Forrestal M J, Frew D J, Hickerson J P, et al. Penetration of concrete targets with deceleration-time measurements[J]. International Journal of Impact Engineering, 2003, 28(5):479-497. doi: 10.1016/S0734-743X(02)00108-2 [23] 陈小伟, 金建明.动能深侵彻弹的力学设计(Ⅱ):弹靶的相关力学分析与实例[J].爆炸与冲击, 2006, 26(1):71-78. doi: 10.3321/j.issn:1001-1455.2006.01.012Chen Xiaowei, Jin Jianming. Mechanics of structural design of EPW (Ⅱ): Analyses on the design of EPW projectiles, concrete targets and examples[J]. Explosion and Shock Waves, 2006, 26(1):71-78. doi: 10.3321/j.issn:1001-1455.2006.01.012 [24] Wu Hao, Fang Qin, Peng Yong, et al. Hard projectile perforation on the monolithic and segmented RC panels with a rear steel liner[J]. International Journal of Impact Engineering, 2014, 76:232-250. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=68d38b07a3a413e4666ef584536d4659 [25] 黄徐利, 陈小伟, 梁冠军.尖头弹穿甲韧性金属靶模型分析[J].爆炸与冲击, 2011, 31(5):490-496. doi: 10.11883/1001-1455(2011)05-0490-07Huang Xuli, Chen Xiaowei, Liang Guanjun. Analysis on perforation of ductile metallic plates by a rigid sharp-nosed projectile[J].Explosion and Shock Waves, 2011, 31(5):490-496. doi: 10.11883/1001-1455(2011)05-0490-07 -
点击查看大图
计量
- 文章访问数: 4550
- HTML全文浏览量: 1203
- PDF下载量: 550
- 被引次数: 0