Numerical simulation of fracture toughness test under high strain rate
-
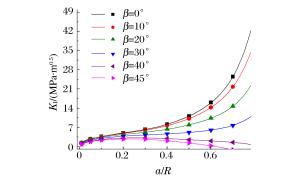
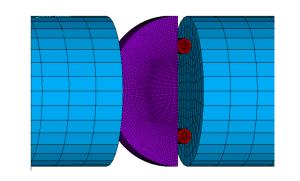
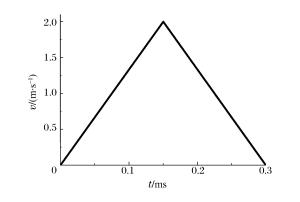
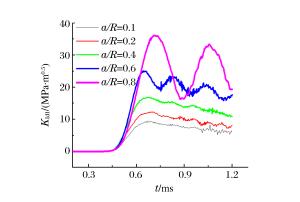
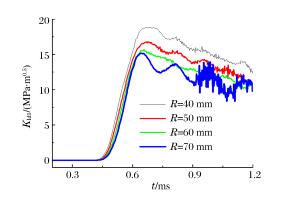
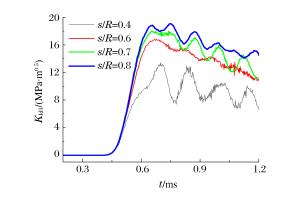
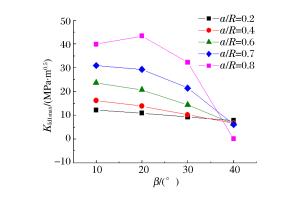
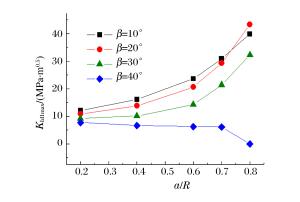
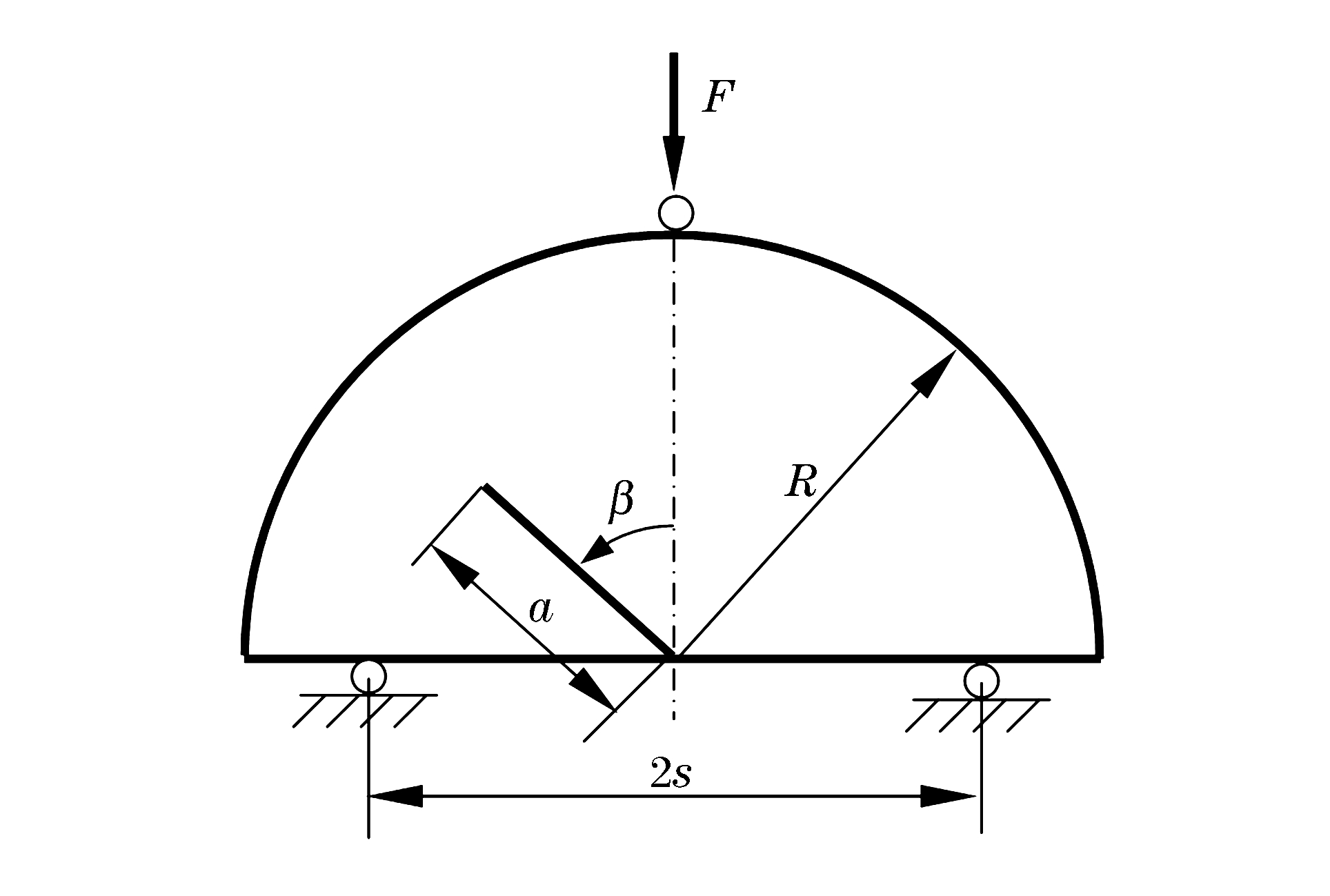
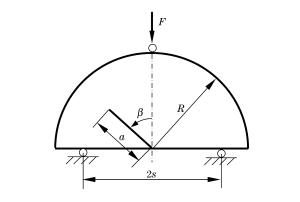
摘要: 采用有限元软件ANSYS/LS-DYNA程序对静态和冲击荷载作用下的含裂纹半圆弯曲(SCB)实验进行了数值模拟。根据静态实验的模拟结果，提出了适合复合型加载的Ⅰ型应力强度因子拟合公式，采用该公式计算应力强度因子的最大误差不超过10%。动态实验的模拟结果表明：对于纯Ⅰ型加载的SCB实验，动态应力强度因子随着试样半径、支座间距以及相对裂纹长度的变化呈现规律性变化；当试样半径小于60mm、相对支座间距为1.2、相对裂纹长度在0.1~0.4范围内时，惯性效应的影响较小，采用静态拟合公式计算裂尖的动态应力强度因子的误差约10%；对于复合型加载的SCB实验，当相对裂纹长度为0.2~0.4、裂纹倾角在10°~40°范围内时，采用静态拟合公式计算裂尖的动态应力强度因子的误差小于10%。Abstract: In this work we conducted numerical simulations of semi-circular bending (SCB) test of steel with cracks respectively in a static condition and under impact loading, using ANSYS/LS-DYNA, a finite element software. According to the results achieved from the simulation of the static test, we have put forward the formula for the calculation of Steel Ⅰ's fitted stress intensity factor which, when applied to the calculation of the factor under the mixed-mode loading, can keep the maximum error below 10%. The simulation result of dynamic test shows that: for semi-circular bending (SCB) test of pure Steel Ⅰ under impact loading, the dynamic stress intensity factor exhibits regular variation with the change in the specimen's radius, the distance between the supports, and the relative crack length: When the specimen's radius is less than 60 mm, the distance between two supports is 1.2 and the relative crack length is in the range of 0.1 to 0.4, the inertial effect is relatively small and the error of the dynamic stress intensity factor calculated with the above formula is about 10%; when the relative crack length is 0.2 to 0.4 and the crack angle is in the range of 10° to 40°, the error of KId which is calculated with this formula is less than 10% for semi-circular bending (SCB) test under mixed-mode loading.
-
图 2 静态复合型加载SCB实验应力强度因子拟合结果
Figure 2. Fitted effect of stress intensity factor in static SCB test under mixed mode loading
图 3 基于SHPB装置的动态SCB实验有限元模型
Figure 3. Finite element model of dynamic SCB test based on SHPB device
图 5 不同相对裂纹长度下的应力强度因子变化规律
Figure 5. Variation of stress intensity factor for different relative crack lengths
图 6 不同试样半径下应力强度因子的变化规律
Figure 6. Variation of stress intensity factor for different sample radiuses
图 7 不同支座间距下应力强度因子的变化规律
Figure 7. Variation of stress intensity factor for different distances between two supports
图 11 KⅠd1max随裂纹相对长度a/R的变化规律
Figure 11. Variation of KⅠd1max with relative crack length a/R
表 1 复合型加载下静态公式计算KⅠdmax的相对误差δm
Table 1. Relative errorδm of KⅠdmax in the static formula under mixed-mode loading
β/(°) δm/% a/R=0.2 a/R=0.4 a/R=0.6 a/R=0.7 a/R=0.8 10 9.6 6.6 -0.7 3.7 26.8 20 6.4 9.8 19.8 23.2 40.3 30 5.4 5.6 24.1 39.2 49.1 40 9.3 0.9 17.2 34.8 138.0 
下载: 导出CSV
-
[1] Nakano M, Kashida K, Yamauchi Y, et al. Dynamic fracture initiation in brittle materials under combined mode Ⅰ/Ⅱ loading[J]. Journal De Physique IV, 1994, 4(8):695-700. [2] Yamauchi Y, Nakano M, Kishida K, et al.Measurement of fracture toughness for brittle materials under mixed-mode impact loading using center-notched disk specimen[J]. Journal of the Society of Materials Science Japan, 2000, 49(12):1324-1329. doi: 10.2472/jsms.49.1324 [3] Ayatollahi M R, Aliha M R M, Hassani M M. Mixed mode brittle fracture in PMMA-An experimental study using SCB specimens[J]. Materials Science and Engineering A, 2006, 417(1/2):348-356. http://www.sciencedirect.com/science/article/pii/S0921509305013821 [4] Ayatollahi M R, Aliha M R M. On determination of mode Ⅱ fracture toughness using semi-circular bend specimen[J]. International Journal of Solids and Structures, 2006, 43(17):5217-5227. doi: 10.1016/j.ijsolstr.2005.07.049 [5] Aliha M R M, Ayatollahi, M R. Mixed mode Ⅰ/Ⅱ brittle fracture evaluation of marble using SCB specimen[J]. Procedia Engineering, 2011, 10:311-318. doi: 10.1016/j.proeng.2011.04.054 [6] Chen R, Xia K W, Dai F et al. Determination of dynamic fracture parameters using a semi-circular bend technique in split Hopkinson pressure bar testing[J]. Engineering Fracture Mechanics, 2009, 76(9):1268-1276. doi: 10.1016/j.engfracmech.2009.02.001 [7] Dai F, Xia K W, et al. Rate dependence of the flexural tensile strength of Laurentian granite[J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(3):469-475. doi: 10.1016/j.ijrmms.2009.05.001 [8] Dai F, Xia K W, et al. Determination of dynamic rock Mode-I fracture parameters using cracked chevron notched semi-circular bend specimen[J]. Engineering Fracture Mechanics, 2011, 78(15):2633-2644. doi: 10.1016/j.engfracmech.2011.06.022 [9] Yau J, Wang S, Corten H. A mixed-mode crack analysis of isotropic solids using conservation laws of elasticity[J]. Journal of Applied Mechanics, 1980, 47(2):335-341. doi: 10.1115/1.3153665 [10] 巫绪涛, 杨伯源.数值外插法求解空间裂纹应力强度因子的研究[J].合肥工业大学学报, 1999, 22(4):26-31. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199901178006Wu Xutao, Yang Boyuan. Study on the numerical extrapolated method for calculating the 3-D crack front stress intensity factor[J]. Journal of Hefei University of Tchnology, 1999, 22(4):26-31. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199901178006 -
计量
- 文章访问数: 5454
- HTML全文浏览量: 1772
- PDF下载量: 713
- 被引次数: 0