Investigation on concrete dynamic bending intensity and limit flexural intensity
-
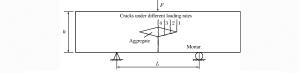
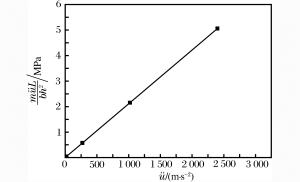
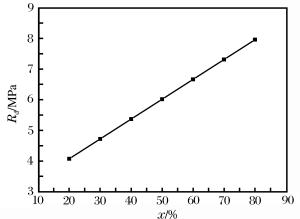
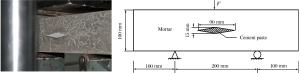
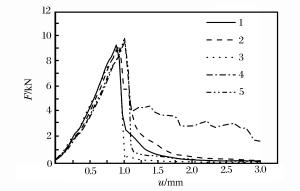
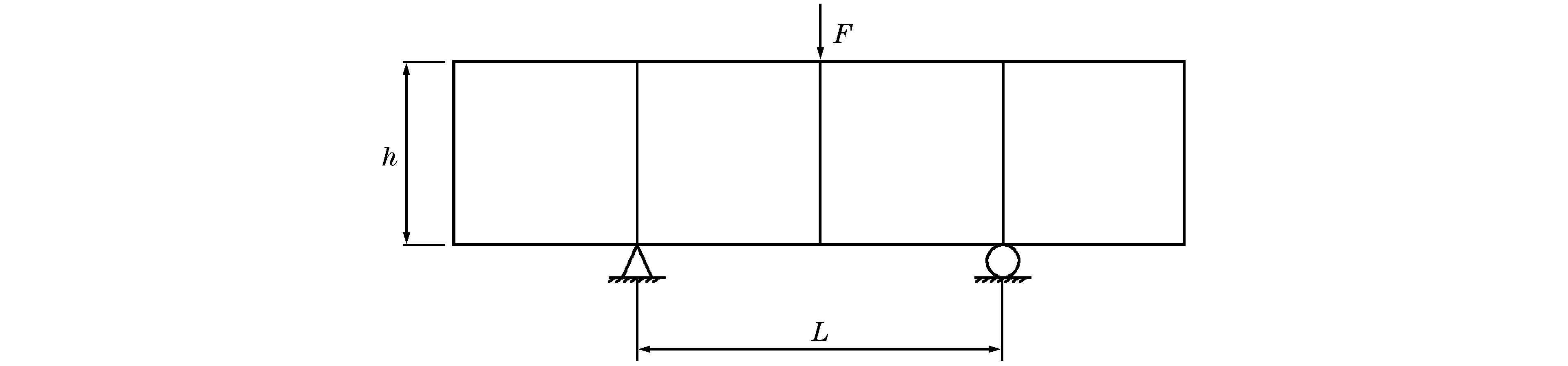
摘要: 混凝土类不均匀脆性材料的率敏感性主要是由于混凝土的不均匀性造成的，不均匀性使得不同速率的动裂纹发展路径不同，决定了不同速率的抗折动强度不同。基于此，提出混凝土抗折动强度由砂浆与骨料的抗折静强度的加权平均值再加上惯性项组成的代数表达式，并预测混凝土材料在爆炸冲击荷载条件下的极限抗折动强度。最后通过特殊设计的单一菱形净浆骨料三点弯实验, 验证了不同加载速率时破坏裂纹的发展路径及抗折动强度变化规律。Abstract: The rate sensitivity of concrete-like brittle materials results mainly from their inhomogeneity, which leads to their different paths of crack development at different load rates and accounts for their different dynamic flexural strengths. On the basis of the above theoretical analysis, this paper presents the algebraic expression of the dynamic flexural strength, which consists of the weighted average of the flexural strength of mortar and aggregate and the inertia term, predicts the limit flexural intensity of concrete materials under different impact loads and, finally, investigates their crack paths and intensity variations at different loading rates by the three-point bending beam test with a special rhombus aggregate.
-
Key words:
- solid mechanics /
- inhomogeneity /
- dynamic bending intensity /
- impact load /
- rate effect
-
图 1 理想均质脆性材料三点弯曲实验示意图
Figure 1. A schematic diagram for three-point-bending test of ideal homogeneous brittle materials
图 2 理想不均匀材料三点弯曲裂纹模型示意图
Figure 2. A schematic diagram for ideal three-point bending crack model of uneven materials
图 3 惯性引起的混凝土抗折动强度
Figure 3. The improvement of concrete dynamic flexural strength caused by the inertia
图 4 混凝土抗折动强度和骨料率的关系
Figure 4. Relationship between dynamic flexural strength and aggregate ratio of concrete
图 5 三点抗弯实验加载和试件尺寸示意图
Figure 5. Schematic diagrams for the three-point-bending test and specimen sizes
表 1 混凝土各相组分材料参数
Table 1. The parameters of concrete materials
材料 E/GPa ν Rs/MPa 骨料 58.731 0.241 9.25 砂浆 17.458 0.196 2.78 粘结界面 13.967 0.200 1.56 
下载: 导出CSV
-
[1] 戚承志, 钱七虎.岩石等脆性材料动力强度依赖应变率的物理机制[J].岩石力学与工程学报, 2003, 22(2):177-181. doi: 10.3321/j.issn:1000-6915.2003.02.002Qi Chengzhi, Qian Qihu. Physical mechanism of dependence of material strength on strain rate for rock like material[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(2):177-181. doi: 10.3321/j.issn:1000-6915.2003.02.002 [2] 丁卫华, 陈厚群, 刘少聪, 等.基于CT的混凝土动力破坏过程的试验研究[J].水力发电, 2009, 35(5):21-23. http://d.old.wanfangdata.com.cn/Periodical/slfd200905006Ding Weihua, Chen Houqun, Liu Shaocong, et al. Test and study on dynamic damage process of concrete based on computed tomography[J]. Water Power, 2009, 35(5):21-23. http://d.old.wanfangdata.com.cn/Periodical/slfd200905006 [3] Kaplan S A. Factors affecting the relationship between rate of loading and measured compressive strength of concrete[J]. Magazine of Concrete Research, 1980, 32(111):79-88. doi: 10.1680/macr.1980.32.111.79 [4] 李庆斌, 郑丹.混凝土动力强度提高的机理探讨[J].工程力学, 2005, 22(S1):188-193. http://d.old.wanfangdata.com.cn/Conference/6029052Li Qingbin, Zheng Dan. Micro-mechanism on the enhancement of dynamic strength for concrete[J]. Engineering Mechanics, 2005, 22(S1):188-193. http://d.old.wanfangdata.com.cn/Conference/6029052 [5] 马怀发, 王立涛, 陈厚群, 等.混凝土动态损伤的滞后特性[J].水利学报, 2010, 41(6):659-664. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slxb201006005Ma Huaifa, Wang Litao, Chen Houqun, et al. Mechanism of dynamic damage delay characteristic of concrete[J]. Journal of Hydraulic Engineering, 2010, 41(6):659-664. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=slxb201006005 [6] 马怀发, 陈厚群, 徐树峰.预静载作用下混凝土动态强度数值分析[J].水利学报, 2012(S1):37-45. http://d.old.wanfangdata.com.cn/Periodical/slxb2012z1007Ma Huaifa, Chen Houqun, Xu Shufeng. Numerical analysis of concrete dynamic strength with static preload[J]. Journal of Hydraulic Engineering, 2012(S1):37-45. http://d.old.wanfangdata.com.cn/Periodical/slxb2012z1007 [7] 梁昕宇, 党发宁, 田威, 等.不同加载率对混凝土试件动力特性的影响研究[J].水力发电学报, 2009, 28(5):35-40. http://d.old.wanfangdata.com.cn/Conference/7813238Liang Xinyu, Dang Faning, Tian Wei, et al. Dynamic property influences and studies of concrete cylinder at different loading rates[J]. Journal of Hydroelectric Engineering, 2009, 28(5):35-40. http://d.old.wanfangdata.com.cn/Conference/7813238 [8] 杜成斌, 孙立国, 江守燕, 等.全级配混凝土梁动强度提高机理研究[J].河海大学学报:自然科学版, 2012, 40(3):294-299. http://d.old.wanfangdata.com.cn/Periodical/hhdxxb201203009Du Chengbin, Sun Liguo, Jiang Shouyan, et al. Dynamic strength enhancement mechanism of a fully-graded concrete beam[J]. Journal of Hohai University: Natural Sciences, 2012, 40(3):294-299. http://d.old.wanfangdata.com.cn/Periodical/hhdxxb201203009 [9] 秦川, 武明鑫, 张楚汉.混凝土冲击劈拉实验与细观离散元数值仿真[J].水力发电学报, 2013, 32(1):196-205. http://d.old.wanfangdata.com.cn/Periodical/slfdxb201301032Qin Chuan, Wu Mingxin, Zhang Chuhan. Impact splitting tensile experiments of concrete and numerical modeling by meso-scale discrete elements[J]. Journal of Hydroelectric Engineering, 2013, 32(1):196-205. http://d.old.wanfangdata.com.cn/Periodical/slfdxb201301032 [10] 严成, 欧卓成, 段卓平, 等.脆性材料动态强度应变率效应[J].爆炸与冲击, 2011, 31(4):423-427. doi: 10.11883/1001-1455(2011)04-0423-05Yan Cheng, Ou Zhuocheng, Duan Zhuoping, et al. Strain-rate effects on dynamic strength of brittle materials[J].Explosion and Shock Waves, 2011, 31(4):423-427. doi: 10.11883/1001-1455(2011)04-0423-05 -
计量
- 文章访问数: 4181
- HTML全文浏览量: 1098
- PDF下载量: 520
- 被引次数: 0