Theoretical and numerical study on detonation wave Mach reflection in high explosive charge with waveshaper
-
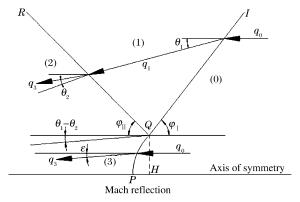
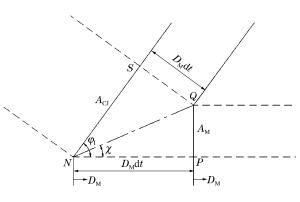
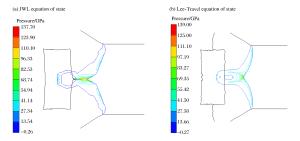
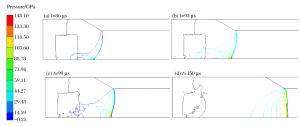
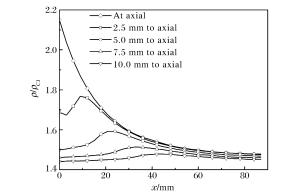
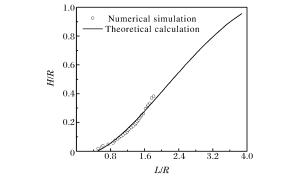
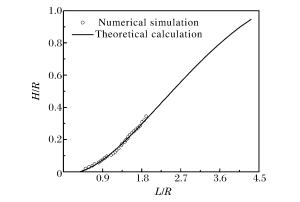
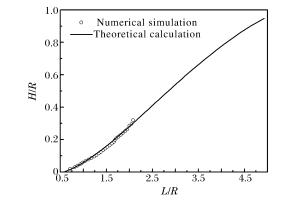
摘要: 基于三波理论和Whitham方法对带隔板装药爆轰波相互作用后发生的正规反射和非正规反射进行了理论分析，给出了爆轰波发生马赫反射时临界入射角和马赫杆增长角等参数的变化规律，提出了马赫杆高度的计算模型。基于凝聚炸药爆轰Jones-Wilkins-Lee(JWL)模型和冲击起爆的Lee-Tarver模型，利用有限元计算软件对带隔板装药爆轰波的传播过程进行了数值模拟。结果表明，发生马赫反射后，随着爆轰波的传播，马赫杆的高度不断增加。数值模拟结果与理论计算结果吻合较好，说明本文中采用的理论模型和数值模拟方法能够较准确地描述带隔板装药爆轰波马赫反射的传播过程。Abstract: On the basis of the three-wave theory and Whitham's method, the flow fields associated with regular reflection and Mach reflection in high explosives with waveshapers were investigated, and the relevant theoretical model for deriving the detonation configuration was proposed. The calculated results of pressure, flow velocity and triple point growth angle of Mach stem were presented and the Mach stem height was also determined based on the modified Whitham's method. The finite element code was used to numerically simulate the detonation processes of the high explosives with waveshapers. The shock initiation of the cylindrical charge was described by the Jones-Wilkins-Lee(JWL) and Lee-Travel models. The calculated results show that the Mach stem height increases with the propagation of detonation wave. The numerical results are consistent with the predictions based on the presented model, which shows that the analytical model provides reasonably accurate predictions of the Mach reflection process.
-
图 1 带隔板柱形装药结构及爆轰波示意图
Figure 1. Schematic diagram for cylindrical charge with waveshaper and detonation wave
图 3 马赫反射临界入射角随多方指数的变化
Figure 3. Critical incident angle for the onset of Mach reflection varying with polytropic exponent
图 4 马赫反射后爆轰波形位置与其垂直射线的关系简图
Figure 4. Relationship of detonation wave and its vertical line after Mach reflection
图 5 马赫杆高度随入射角变化的计算结果
Figure 5. Calculated variation of Mach stem height with incident angle
图 6 带隔板装药数值模拟的有限元模型
Figure 6. A finite element model for numerical simulation on charge with waveshaper
图 7 采用不同的炸药状态方程模拟得到的爆轰波波形
Figure 7. Detonation waveform of explosive simulated by different equations of state
图 9 马赫反射发生后，随着爆轰波的传播，在轴线不同位置处压力的变化
Figure 9. Pressure at different positions of the axis after Mach reflection
图 10 马赫反射发生后，随着爆轰波的传播，在轴线不同位置处密度的变化
Figure 10. Density at different positions of the axis after Mach reflection
表 1 不同炸药装药中发生马赫反射时临界入射角的计算值与实验结果
Table 1. Calculated and experimental results of critical incident angles corresponding to Mach reflection in different explosive charges
下载: 导出CSV
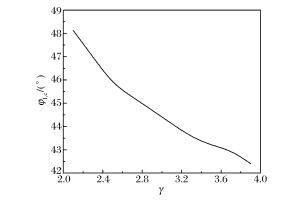
φⅠ/(°) DCJ/(km·s-1) DM, exp/(km·s-1) DM, cal/(km·s-1) $\frac{{{D_{{\rm{M, exp}}}} - {D_{{\rm{M, cal}}}}}}{{{D_{{\rm{M, exp}}}}}}/\% $ z χexp/(°) χcal/(°) $\frac{{{\chi _{{\rm{exp}}}} - {\chi _{{\rm{cal}}}}}}{{{\chi _{{\rm{exp}}}}}}/\% $ 46.5 4.14 5.89 5.86 0.5 3.42 1.5 1.55 -3.2 48.5 4.20 5.77 5.79 -0.3 3.22 2.27 2.13 6.6 49.5 4.48 6.07 6.11 -0.7 3.13 2.80 2.45 14.3
下载: 导出CSV
-
[1] Dowker J S. Quantum mechanics on group space and Huygens' principle[J]. Annals of Physics, 1971, 62(2):361-382. doi: 10.1016/0003-4916(71)90096-0 [2] 汤明钧, 杨全中, 阎秀华.破甲弹中爆轰波相互作用的初步研究[J].南京理工大学学报:自然科学版, 1979(1):145-156. http://www.cnki.com.cn/Article/CJFDTOTAL-NJLG197901008.htmTang Mingjun, Yang Quanzhong, Yan Xiuhua. Preliminary study of detonation wave interaction in HEAT[J]. Journal of Nanjing University of Science Technology:Nature Science, 1979(1):145-156. http://www.cnki.com.cn/Article/CJFDTOTAL-NJLG197901008.htm [3] 杨全中, 范宝春, 杨崇惠.带隔板装药中爆轰波的相互作用[J].南京理工大学学报:然科学版, 1982(2):23-30. http://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201604003.htmYang Quanzhong, Fan Baochun, Yang Chonghui. Interaction of the detonation waves in the explosive charge with the inserter[J]. Journal of Nanjing University of Science Technology:Nature Science, 1982(2):23-30. http://www.cnki.com.cn/Article/CJFDTOTAL-BZCJ201604003.htm [4] Whitham G B. A new approach to problems of shock dynamics:Part Ⅰ:Two-dimension problem[J]. Journal of Fluid Mechanics, 1957, 2(2):145-171. doi: 10.1017/S002211205700004X [5] Dunne B B. Mach reflection of detonation waves in condensed high explosives:Ⅰ[J]. Physics of Fluids, 1961, 4(7):918-933. doi: 10.1063/1.1706425 [6] Hull L M. Mach reflection of spherical detonation waves[C]//Short J M. Proceedings of the 10th International Symposium on Detonationm. Boston: Plenum Publishing Corporation, 1993: 12-16. [7] 张俊秀, 恽寿榕.凝聚炸药中爆轰波马赫反射的实验研究[J].爆炸与冲击, 1986, 6(3):208-213. http://www.bzycj.cn/article/id/11076Zhang Junxiu, Yun Shourong. Experimental investigations of the Mach relection in a condensed explosive[J]. Explosion and Shock Waves, 1986, 6(3):208-213. http://www.bzycj.cn/article/id/11076 [8] Zhang Xianfeng, Huang Zhengxiang, Qiao Liang. Detonation wave propagation in double-layer cylindrical high explosive charge[J]. Propellants, Explosives, Pyrotechnics, 2011, 36(3):210-218. doi: 10.1002/prep.v36.3 [9] 张先锋, 丁建宝, 赵晓宁.夹层装药作用过程的数字模拟[J].爆炸与冲击, 2009, 29(6):617-624. doi: 10.3321/j.issn:1001-1455.2009.06.011Zhang Xianfeng, Ding Jianbao, Zhao Xiaoning. Numberical simulation of duble layer shaped charge[J]. Explosion and Shock Waves, 2009, 29(6):617-624. doi: 10.3321/j.issn:1001-1455.2009.06.011 [10] Murphy M J, Lee E L, Weston A M. Modeling shock initiation in composition B[C]//Short J M. Proceedings of the 10th International Symposium on Detonationm. Boston: Plenum Publishing Corporation, 1992: 965-970. [11] Grasso F, Paoli R. An analytical study of mach reflection in nonequilibrium steady flows[J]. Physics of Fluids, 1999, 11(10):3150-3167. doi: 10.1063/1.870172 [12] Sternberg H M, Piacesi D. Interaction of oblique detonation waves with iron[J]. Physics of Fluids, 1966, 9(7):1307-1315. doi: 10.1063/1.1761845 [13] Whithan G B. Liner and nonlinear waves[M]. New York:John Wiley & Sons Press, 1974:263-274. [14] Lambourn B D, Wright P W.Mach interaction of two plane detonation waves[C]//Proceeding of the Fourth International Symposium on Detonation. 1965: 142-152. [15] Lee E, Finger M, Collins W. JWL equation of state coefficients for high explosives[R]. Livermore: Lawrence Livermore Laboratory, 1973. [16] Davison L, Horie Y, Shahinpoor M. High-pressure shock compression of solids[M]. Springer Science & Business Media, 2012:123-143. -
点击查看大图
计量
- 文章访问数: 4527
- HTML全文浏览量: 1550
- PDF下载量: 538
- 被引次数: 0