PVDF应力测试技术及其在多孔材料爆炸冲击实验中的应用

胡亚峰; 刘建青; 顾文彬; 金建峰

doi:10.11883/1001-1455(2016)05-0655-08

PVDF应力测试技术及其在多孔材料爆炸冲击实验中的应用

doi: 10.11883/1001-1455(2016)05-0655-08

1.
中国华阴兵器试验中心，陕西华阴 714200
2.
解放军理工大学，江苏南京 210007

基金项目:

爆炸冲击防灾减灾国家重点实验室开放基金项目 DPMEIKF201407

详细信息

作者简介:
胡亚峰(1988—)，男，硕士，工程师, 827734300@qq.com

中图分类号: O384
计量
- 文章访问数: 4339
- HTML全文浏览量: 1225
- PDF下载量: 601
- 被引次数: 0
出版历程
- 收稿日期: 2015-03-24
- 修回日期: 2015-05-22
- 刊出日期: 2016-09-25

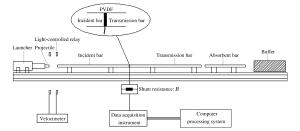
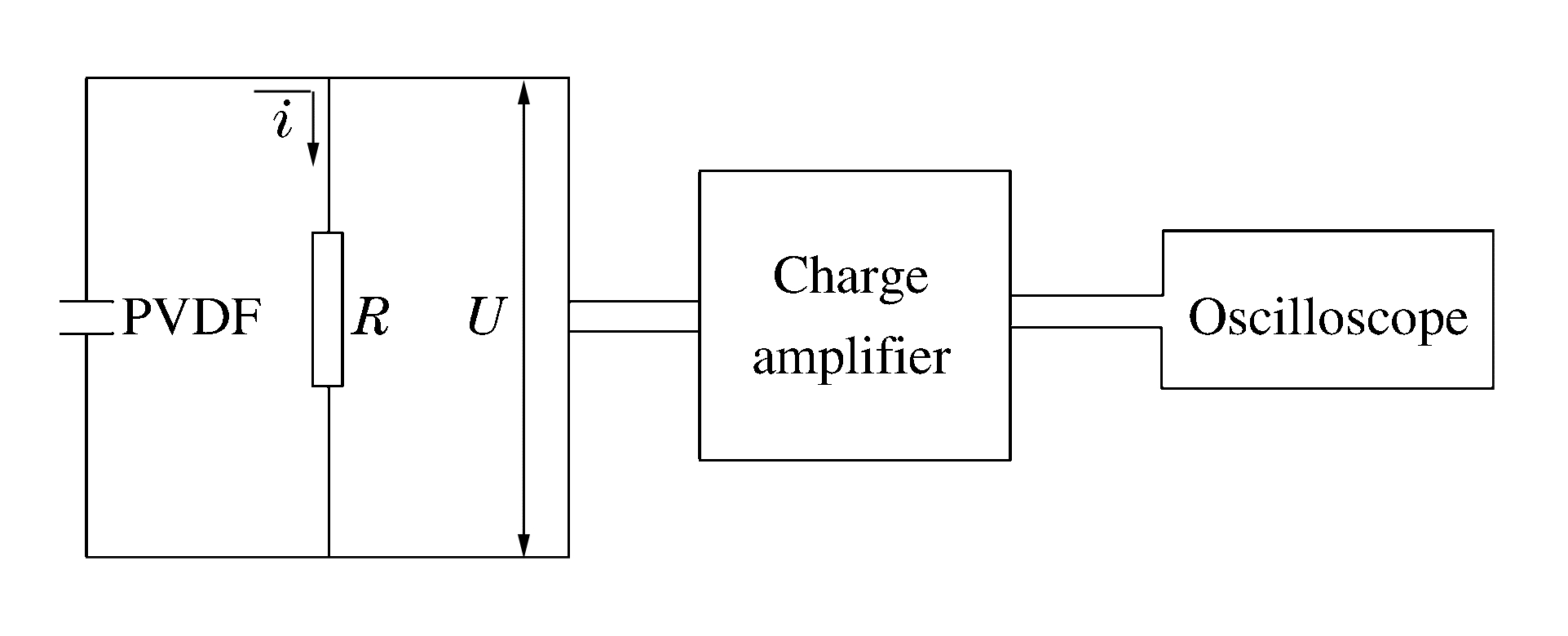
Stress-testing method by PVDF gauge and its application in explosive test of porous material

1.
Huayin Ordnance Test Center, Huayin 714200, Shanxi, China
2.
PLA University of Science and Technology, Nanjing 210007, Jiangsu, China

摘要

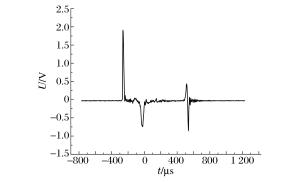
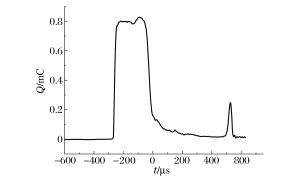
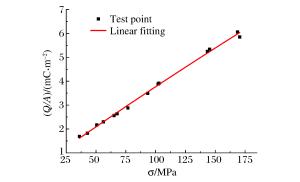
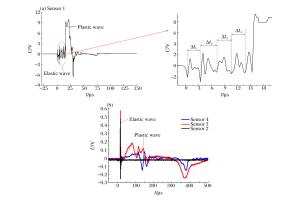
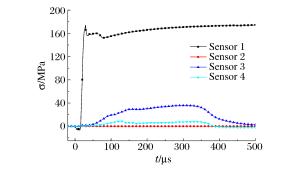
摘要: 通过精确测量Hopkinson杆子弹速度，实现了对PVDF压力传感器的动态标定，测试数据线性度良好，误差不超过1.9%，得到动态灵敏度系数K=32.83 pC/N，采用500 g TNT对“钢板-泡沫铝-钢板”复合结构进行爆炸冲击加载，测量结构间应力波的传播情况。研究结果表明：电压测试信号可以较为准确地反映弹性波与塑性波的加载时间和传播速度，PVDF对弹性应力波段高频信号的动态响应灵敏准确，与理论数据的相对误差为3.5%。测得泡沫铝材料中塑性波的传播速度为590 m/s，A₁-B₁界面塑性波透射系数达到了0.53，远高于弹性波透射系数。从机理上对应力时程曲线中出现的特殊现象进行了阐述，为相关爆炸测试提供参考。
- 爆炸力学 /
- 爆炸测试 /
- 泡沫铝 /
- PVDF传感器
Abstract: In this work, by accurately measuring the bullet speed of the Hopkinson bar, we succeeded in the dynamic calibration of the PVDF pressure sensor. The test data obtained have a good linearity and a deviation below 1.9%. The coefficient value K of dynamic sensitivity is 32.83 pC/N. By applying a blast loading of 500 g TNT to the composite structure of "steel-aluminum foam-steel", the propagation of the stress wave between its components was measured. The results show that the voltage signal can accurately represent the loading time and the propagation velocity of the elastic wave and plastic wave and the PVDF dynamic response of elastic stress wave with high-frequency signal is sensitive and accurate, with only a relative deviation of less than 3.5% from the theoretical data. The measured propagation velocity of the plastic wave in the aluminum foam is 590 m/s, the transmission coefficient of the plastic wave in A1-B1 interface is 0.53, which is much higher than that of the elastic wave. Special remarks were made concerning the unusual phenomena observed in the stress curve based upon our understanding of the mechanism, providing a reference for relevant explosion tests.
- mechanics of explosion /
- explosion test /
- aluminum foam /
- PVDF sensor

HTML全文

图 1 电流模式测量电路

Figure 1. Measuring circuit based on current mode

下载: 全尺寸图片幻灯片

图 2 PVDF传感器标定系统

Figure 2. System for calibrating PVDF sensors

下载: 全尺寸图片幻灯片

图 3 脉冲应力对PVDF传感器的作用过程

Figure 3. Mechanism of stress wave on PVDF sensors

下载: 全尺寸图片幻灯片

图 4 Hopkinson杆冲击的电压信号

Figure 4. Voltage signal of Hopkinson bar impacting

下载: 全尺寸图片幻灯片

图 5 电压信号的积分曲线

Figure 5. Integral curve of voltage signal

下载: 全尺寸图片幻灯片

图 6 总体线性拟合

Figure 6. Overall linear fitting

下载: 全尺寸图片幻灯片

图 7 分组线性拟合

Figure 7. Group linear fitting

下载: 全尺寸图片幻灯片

图 8 实验装置示意图

Figure 8. Sketch of experimental apparatus

下载: 全尺寸图片幻灯片

图 9 实验现场

Figure 9. Testing site

下载: 全尺寸图片幻灯片

图 10 泡沫铝变形情况

Figure 10. Deformation of aluminum foam

下载: 全尺寸图片幻灯片

图 11 实验所测电压信号

Figure 11. Voltage signal of test

下载: 全尺寸图片幻灯片

图 12 积分所得应力时程曲线

Figure 12. Time history curves of stress by integration

下载: 全尺寸图片幻灯片

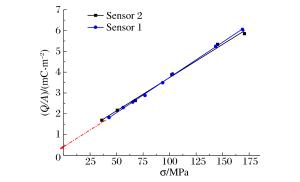
表 1 Hopkinson杆冲击测试数据

Table 1. Measurement data of Hopkinson bar impacting

传感器1			传感器2
v/(m·s^-1)	σ/MPa	Ω_max/pC	v/(m·s^-1)	σ/MPa	Ω_max/pC
8.03	56	2 300	9.67	68	2 640
6.12	43	1 820	7.24	51	2 170
9.31	65	2 560	5.16	36	1 690
10.97	77	2 880	14.60	102	3 880
13.35	93	3 490	20.76	145	5 340
14.69	103	3 910	24.38	171	5 850
20.50	143	5 240
24.11	169	6 060

下载: 导出CSV

表 2 实验相关参数(炸高15 cm)

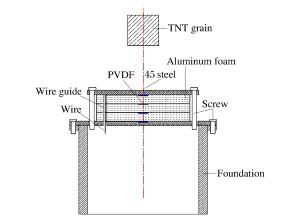
Table 2. Related parameters(blasting height: 15 cm)

泡沫铝	δ/%	ρ/(g·cm^-3)	d/mm	传感器	布设位置	R/Ω
B1	84.5	0.418 5	2.5	1	A1-B1	42.68
B2	80.8	0.518 4	2.0	2	B1-B2	43.02
B3	77.6	0.604 8	2.0	3	B2-B3	42.28

下载: 导出CSV

参考文献(15)

[1]	Kawai H. The piezoelectricity of polyvinyldene fluoride[J]. Journal of Applied Physics, 1969, 8(7):975-976. doi: 10.1143/JJAP.8.975
[2]	Graham R A, Anderson M U, Bauer F, et al. Piezoelectric polarization of the ferroelectric polymer PVDF from 10 MPa to 10 GPa: Studies of loading-path dependence[C]//Shock Compression of Condensed Matter-1991. Williamsburg, Virginia, 1992: 883-886. https://www.sciencedirect.com/science/article/pii/B978044489732950203X
[3]	Bauer F. Advances in piezoelectric PVDF shock compression sensors[C]//10th International Symposium on Electrets. Greece: IEEE Stands Office, 1999: 647-650. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=832129
[4]	Bauer F. PVDF shock sensors: Applications to polar materials and high explosives[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2000, 47(6):1448-1454. doi: 10.1109/58.883534
[5]	Sokhanvar S, Dargahi J, Packirisamy M. Influence of friction on piezoelectric sensors[J]. Sensors & Actuators A Physical, 2008, 141(1):120-128. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e7e4fd12958a1a28042606d90f80f6c4
[6]	Shirinov A V, Schomburg W K. Pressure sensor from a PVDF film[J]. Sensors & Actuators A Physical, 2008, 142(1):48-55. doi: 10.1007-s10725-010-9536-z/
[7]	席道瑛, 郑永来.PVDF压电计在动态应力利测量中的应用[J].爆炸与冲击, 1995, 15(2):174-179. http://www.bzycj.cn/article/id/10573 Xi Daoying, Zheng Yonglai. Application of PVDF gauges to dynamical stress measurements[J]. Explosion and Shock Waves, 1995, 15(2):174-179. http://www.bzycj.cn/article/id/10573
[8]	李焰, 张向荣, 谭红梅, 等.国产PVDF压电薄膜的冲击加载及卸载响应研究[J].高压物理学报, 2004, 18(3):261-266. doi: 10.3969/j.issn.1000-5773.2004.03.011 Li Yan, Zhang Xiangrong, Tan Hongmei, et al. Response of homemade PVDF piezofilm under shock loading and unloading[J]. Chinese Journal of High Pressure Physics, 2004, 18(3):261-266. doi: 10.3969/j.issn.1000-5773.2004.03.011
[9]	赵继波, 谭多望, 张远平, 等.PVDF计在水中爆炸近场压力测试中的应用[J].火炸药学报, 2009, 32(3):1-4. doi: 10.3969/j.issn.1007-7812.2009.03.001 Zhao Jibo, Tan Duowang, Zhang Yuanping, et al. Application of PVDF sensor in underwater explosive shock wave measurement at near-field[J]. Chinese Journal of Explosives & Propellants, 2009, 32(3):1-4. doi: 10.3969/j.issn.1007-7812.2009.03.001
[10]	王伟, 李小春.不耦合装药下爆炸应力波传播规律的试验研究[J].岩土力学, 2010, 31(6):1723-1729. doi: 10.3969/j.issn.1000-7598.2010.06.008 Wang Wei, Li Xiaochun. Experimental study of propagation law of explosive stress wave under condition of decouple charge[J]. Rock and Soil Mechanics, 2010, 31(6):1723-1729. doi: 10.3969/j.issn.1000-7598.2010.06.008
[11]	任新见, 陈虎林.PVDF传感器在爆炸近区超压测量中的应用研究[J].振动与冲击, 2012, 31(12):146-149. http://d.old.wanfangdata.com.cn/Periodical/zdycj201212029 Ren Xinjian, Chen Hulin. Application of PVDF sensor in shock wave measurement of near zone of explosion[J]. Journal of Vibration and Shock, 2012, 31(12):146-149. http://d.old.wanfangdata.com.cn/Periodical/zdycj201212029
[12]	王永刚, 胡时胜, 王礼立.爆炸荷载下泡沫铝材料中冲击波衰减特性的实验和数值模拟研究[J].爆炸与冲击, 2003, 32(6):516-523. doi: 10.3321/j.issn:1001-1455.2003.06.006 Wang Yonggang, Hu Shisheng, Wang Lili. Shock attenuation in aluminum foams under explosion loading[J]. Explosion and Shock Waves, 2003, 32(6):516-523. doi: 10.3321/j.issn:1001-1455.2003.06.006
[13]	田杰.泡沫铝的冲击波衰减和抗爆震特性研究[D].合肥: 中国科学技术大学, 2006: 50-66. http://cdmd.cnki.com.cn/Article/CDMD-10358-2006102746.htm
[14]	王礼立.应力波基础[M].北京:国防工业出版社, 1985.
[15]	胡亚峰, 顾文彬, 刘建青, 等.应力波在泡沫铝夹层三明治板中传播规律的数值研究[J].爆破器材, 2014, 43(5):15-23. doi: 10.3969/j.issn.1001-8352.2014.05.004 Hu Yafeng, Gu Wenbin, Liu Jianqing, et al. Numerical study of stress wave propagation rules in aluminum foam sandwich plates[J]. Explosive Materials, 2014, 43(5):15-23. doi: 10.3969/j.issn.1001-8352.2014.05.004