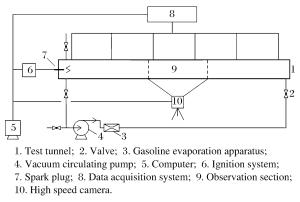
Experimental estimation of the combustion regime in the oil-gas explosion process
-
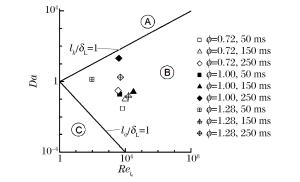
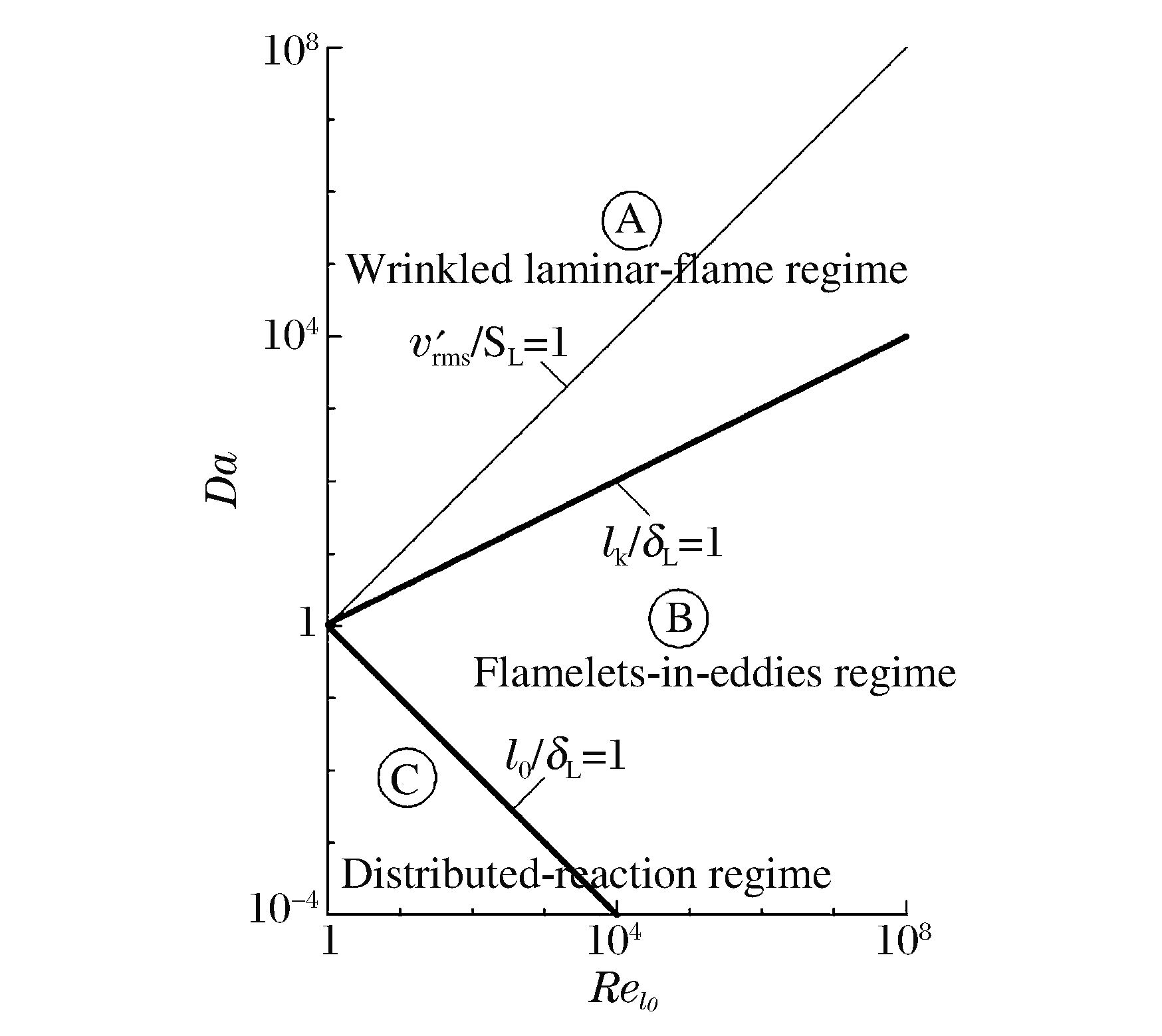
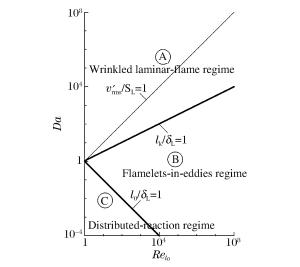
摘要: 首先分析讨论了油气爆炸过程中火焰燃烧模式的估计方法，然后在激波管内进行了低、中、高3次不同初始油气浓度条件下的油气爆炸实验，通过实验数据分别计算出了低、中、高初始油气浓度条件下油气爆炸在初期、中期和后期的丹姆克尔数和湍流雷诺数，最后依靠丹姆克尔数-湍流雷诺数图对低、中、高初始油气浓度条件下油气爆炸初期、中期和后期的火焰燃烧模式进行了定量估计。结果表明：低、中、高初始油气浓度条件下激波管油气爆炸过程初期、中期和后期的火焰燃烧模式均为漩涡内小火焰模式。Abstract: In this artical, firstly, estimation method of flame combustion regime of the oil-gas explosion was discussed and three oil-gas explosion experiments under the conditions of low, middle and high initial gas vapor concentration were carried out, and then the Damköhler number and the turbulent Reynolds number for the early, interim and late stage of the oil-gas explosion at low, middle and high initial gas vapor concentration conditions were calculated according to the experimental data. Finally, through the Damköhler number vs. Reynolds number diagram, the combustion regimes for each stage of the oil-gas explosion at low, middle and high initial gas vapor concentration conditions were quantitative estimated. Results show that the combustions at early, interim and late stage of the gas-air explosion under the conditions of low, middle and high initial gas vapor concentration in the tube have the same regime of flameletes-in-eddies. The conclusions of this paper can provide some useful reference for the further study of combustion regime and the numerical analysis model selection of the gas-oil explosion.
-
图 1 湍流预混火焰的3种模式随Da和Rel0的分布
Figure 1. Distribution of the three turbulence premixed flame models based on values of Da and Rel0
图 3 流场速度和爆炸超压随时间的变化曲线
Figure 3. Variation curves of gas velocity and pressure vs. time
图 4 3组电偶采集到的流场温度随时间的变化曲线
Figure 4. Temperature vs. time curves acquired by the three thermocouples
图 5 油气爆炸过程火焰燃烧模式分布
Figure 5. Distribution of the flame regimes of oil-gas explosion process
图 6 油气爆炸在148、152和156 ms时的火焰高速摄影照片
Figure 6. High speed photos of the flame when the time was 148, 152 and 156 ms
表 1 各时刻激波管内气体流速、压力和已燃气体温度实验数据(ϕ=1)
Table 1. Flow velocity, pressure and burned gas temperature in the shock tube at different times (ϕ=1)
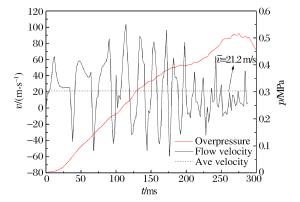
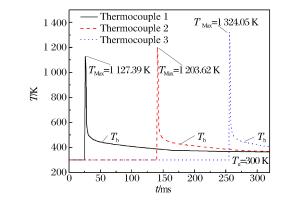
t/ms v/(m·s-1) vrms* p/Pa Tmax/K 50 55.82 34.62 98 530 1 127.39 150 72.76 51.56 340 800 1 203.62 250 29.14 7.94 486 190 1 324.05 
下载: 导出CSV
表 2 参数BM，B2和ϕM取值
Table 2. Value of BM, B2 and ϕM
燃料 ϕM BM/(cm·s-1) B2/(cm·s-1) 甲醇 1.11 36.92 -140.51 丙烷 1.08 34.22 -138.65 异辛烷 1.13 26.32 -84.72 RMFD-303 1.13 27.58 -78.34
下载: 导出CSV
表 3 各时刻的Da和Rel0计算值(ϕ=1)
Table 3. Calculated values of Da & Rel0 at different times (ϕ=1)
t/ms Da Rel0 50 0.19 4 603 150 0.26 31 366 250 21 4 012
下载: 导出CSV
表 4 各时刻激波管内气体流速、压力和已燃气体温度实验数据(ϕ=0.72)
Table 4. Flow velocity, pressure and burned gas temperature in the shock tube at different times (ϕ=0.72)
t/ms v/(m·s-1) vrms* p/Pa Tmax/K 50 65.13 45.45 115 120 1 158.42 150 -5.74 25.42 322 410 1 201.77 250 11.04 8.64 357 380 1 238.51
下载: 导出CSV
表 5 各时刻激波管内气体流速、压力和已燃气体温度实验数据(ϕ=1.28)
Table 5. Flow velocity, pressure and burned gas temperature in the shock tube at different times (ϕ=1.28)
t/ms v/(m·s-1) vrms* p/Pa Tmax/K 50 29.69 7.10 11 510 1 251.63 150 86.91 64.32 227 780 1 296.15 250 12.64 9.95 504 310 1 357.36
下载: 导出CSV
表 6 各时刻的Da和Rel0计算值
Table 6. Calculated values of Da & Rel0 at different times
t/ms Da Rel0 ϕ=0.72 ϕ=1.28 ϕ=0.72 ϕ=1.28 50 0.03 1.31 6 767 93 150 0.10 0.15 9 993 15 838 250 0.31 1.76 3 589 4 970
下载: 导出CSV
-
[1] Steinberg A M, Driscoll J F. Straining and wrinkling processes during turbulence-premixed flame interaction measured using temporally-resolved diagnostics[J]. Combustion and Flame, 2009, 156(12):2285-2306. doi: 10.1016/j.combustflame.2009.06.024 [2] Shin D H, Lieuwen T. Flame wrinkle destruction processes in harmonically forced, laminar premixed flames[J]. Combustion and Flame, 2012, 159(11):3312-3322. doi: 10.1016/j.combustflame.2012.06.015 [3] Yi Y, Geng L, Jing G. Experimental study on the fractal characteristic of methane explosion flame[J]. Safety Science, 2012, 50(4):679-683. doi: 10.1016/j.ssci.2011.08.052 [4] Won S H, Windom B, Jiang B, et al. The role of low temperature fuel chemistry on turbulent flame propagation[J]. Combustion and Flame, 2014, 161(2):475-483. doi: 10.1016/j.combustflame.2013.08.027 [5] Zhang M, Wang J, Wu J, et al. Flame front structure of turbulent premixed flames of syngas oxyfuel mixtures[J]. International Journal of Hydrogen Energy, 2014, 39(10):5176-5185. doi: 10.1016/j.ijhydene.2014.01.038 [6] Mukaiyama K, Shibayama S, Kuwana K. Fractal structures of hydrodynamically unstable and diffusive-thermally unstable flames[J]. Combustion and Flame, 2013, 160(11):2471-2475. doi: 10.1016/j.combustflame.2013.05.017 [7] Williams F A. Asymptotic methods in turbulent combustions[J]. AIAA Journal, 1986, 24:867-875. doi: 10.2514/3.9361 [8] Abraham J, Williams F A, Bracco F V. A discussion of turbulent flame structure in premixed charges[R]. Warrendale, Pennsylvania, USA: Society of automotive engineers, 1985. [9] Zhang P, Du Y, Zhou Y, et al. Explosions of gasoline-air mixture in the tunnels containing branch configuration[J]. Journal of Loss Prevention in the Process Industries, 2013, 26(6):1279-1284. doi: 10.1016/j.jlp.2013.07.003 [10] Yang D, Li Z P, Hong O Y. Effects of humidity, temperature and slow oxidation reactions on the occurrence of gasoline-air explosions[J]. Journal of Fire Protection Engineering, 2013, 23(3):226-238. doi: 10.1177/1042391513486464 [11] 杨辉, 崔鑫, 郑昕等.管道中湍流强度及湍流积分尺度随时间的变化研究[J].安全与环境工程, 2013, 20(4):102-104. doi: 10.3969/j.issn.1671-1556.2013.04.023Yang H, Cui X, Zheng X, et al.Investigation of variation of turbulence intensity and turbulent integral scale with time in tube[J]. Safety and Environmental Engineering, 2013, 20(4):102-104. doi: 10.3969/j.issn.1671-1556.2013.04.023 [12] Sak C, Liu R, Ting D S-K, et al. The role of turbulence length scale and turbulence intensity on forced convection from a heated horizontal circular cylinder[J]. Experimental Thermal and Fluid Science, 2007, 31(4):279-289. doi: 10.1016/j.expthermflusci.2006.04.007 [13] Metghalchi M, Keck J C. Burning velocities of mixtures of air with methanol, isooctane, and indolene at high pressure and temperature[J]. Combustion and Flame, 1982, 48:191-210. doi: 10.1016/0010-2180(82)90127-4 [14] Spadling D B. Combustion and Mass Transfer[M]. New York: Pergamon, 1979:59. [15] Stephen R T. An introduction to combustion:concepts and application[M]. New York: The McGraw-Hill Companies, 2000:appendix C. [16] Ballal D R, Lefebvre A H. The structure and propagation of turbulent flames[J]. Proceedings of the Royoal Society of London, 1979, 344(1637):217-234. http://d.old.wanfangdata.com.cn/OAPaper/oai_arXiv.org_1312.1890 [17] Ballal D R, Lefebvre A H. The structure of a premixed turbulent flame[J]. Proceedings of the Royoal Society of London, 1979, 367(1730):253-280. http://www.jstor.org/stable/79908 [18] Poinsot T, Candel S, Trouvé A. Applications of direct numerical simulation to premixed turbulent combustion[J]. Progress in Energy and Combustion Science, 1995, 21(6):531-576. doi: 10.1016/0360-1285(95)00011-9 -
计量
- 文章访问数: 4594
- HTML全文浏览量: 1227
- PDF下载量: 437
- 被引次数: 0