Numerical simulation of the delay time of impact initiated projectile
-
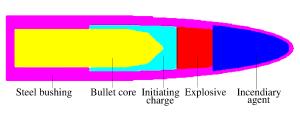
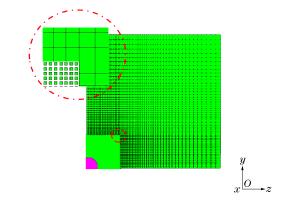
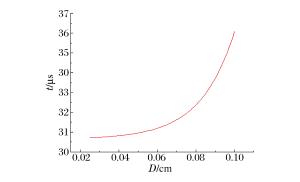
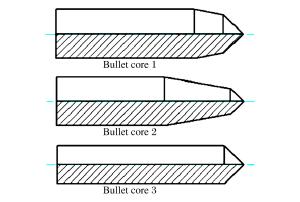
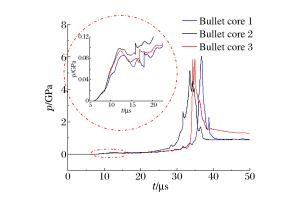
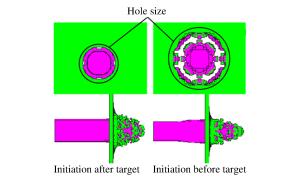
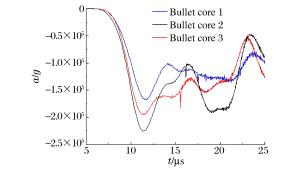
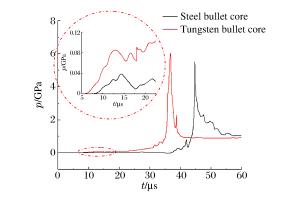
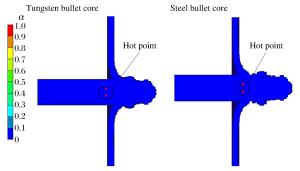
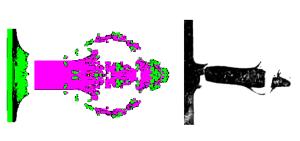
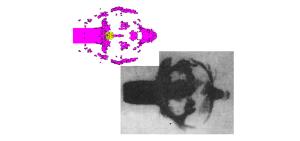
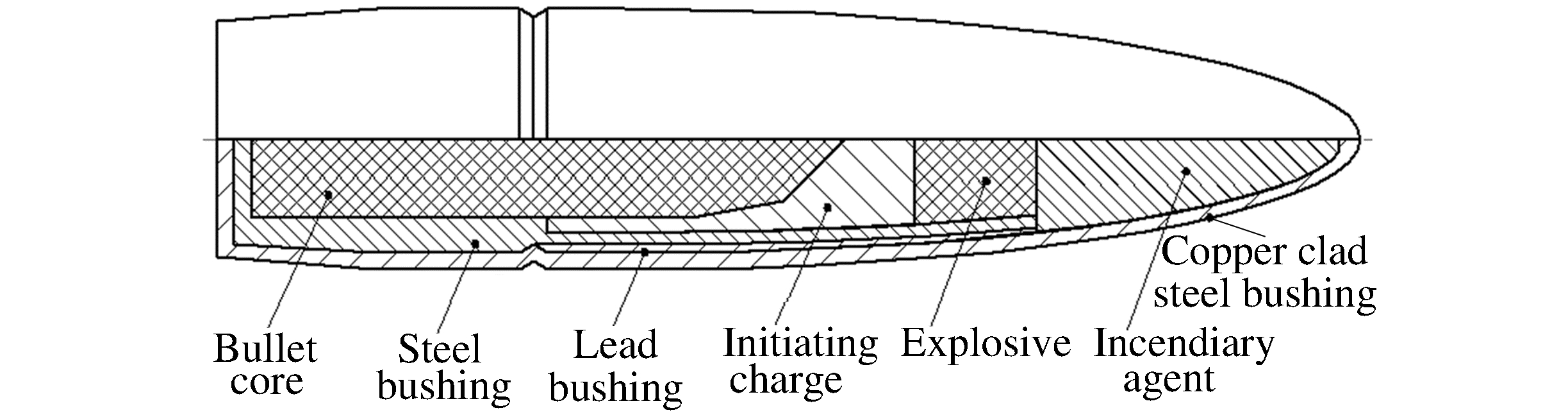
摘要: 对穿爆燃弹的穿靶及释能过程进行数值模拟,解释了SPH-FEM耦合方法在模拟冲击起爆过程的优越性。通过对不同弹芯头部形状、直径及材料的对比分析,得到了不同工况下装药热点成长的压力-时间曲线,计算结果表明:在弹芯直径不变的情况下,弹芯头部直角尖刺越短,装药的热点成长时间越短;在头部尖刺长度不变的情况下,减小弹芯直径,热点生成时间也缩短;选用钢弹芯比钨合金弹芯有一定靶后释能优势。模拟穿靶效果与真实穿靶效果符合较好,这种方法可以为穿爆类弹丸设计提供依据。Abstract: In this work, we investigated the process of penetration and energy release of the impact initiated projectile was investigated using numerical simulation, verified the superiority of the coupling of smooth particle hydrodynamics (SPH) with finite element method (FEM) in impact initiation, and obtained pressure-time curves for the projectile's hot-point pressure growth in different operating conditions by analyzing its bullet core's different head shapes, diameters and materials. Our simulation results show that, for a given bullet core's diameter, the shorter the bullet head's spike length, the more reduced the initiation time for the explosives' hot-point growth; for a given bullet core's length, a reduced bullet core's diameter will lead to a reduced hot-point growth time; and bullet cores made from steel show greater advantage at delay initiation time over those made from tungsten alloy. The simulated effects of target penetration are fairly consistent with those from experimental results.
-
Key words:
- mechanics of explosion /
- impact initiation /
- SPH /
- impact initiated projectile /
- coupling algorithm
-
表 1 PETN和Comp B材料参数
Table 1. Material parameters of PETN and Comp B
炸药 材料参数 产物参数 未反应物参数 I/μs-1 b a x G1 c d y G2 e g z ω A/GPa B/GPa R1 R2 ω A/GPa B/GPa R1 R2 PETN 20 0.222 0 4 0 0 0 0 400 0.222 0.667 1.4 0.25 589.2 16.92 4.4 1.2 1.173 3 746 -131.3 7.2 3.6 Comp B 44 0.222 0.01 4.0 414 0.222 0.667 2.0 0 0 0 0 0.34 524.2 7.67 4.2 1.1 0.893 77 810 -5.031 11.3 1.13 -
[1] 张德良, 罗忠文, 俞善炳, 等.穿爆弹撞靶效应数值分析[J].兵工学报, 1997, 18(2):102-106. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700179225Zhang Deliang, Luo Zhongwen, Yu Shanbin, et al. Numerical analyses of the effects of impact of a penetrating projectile on the target[J]. Acta Armamentarii, 1997, 18(2):102-106. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199700179225 [2] 纪冲, 龙源, 方向.基于FEM-SPH耦合法的弹丸侵彻钢纤维混凝土数值模拟[J].振动与冲击, 2010, 29(7):69-74. doi: 10.3969/j.issn.1000-3835.2010.07.015Ji Chong, Long Yuan, Fang Xiang. Numerical simulation for projectile penetrating steel fiber reinforced concrete with FEM-SPH coupling algorithm[J]. Journal of Vibration and Shock, 2010, 29(7):69-74. doi: 10.3969/j.issn.1000-3835.2010.07.015 [3] Century Dynamics Inc. Interactive non-linear dynamic analysis software AUTODYNTM user manual. Revision 3.0[CP]. USA: Century Dynamics Inc, 1997. [4] 乐莉, 闫军, 钟秋海.超高速撞击仿真算法分析[J].系统仿真学报, 2004, 16(9):1941-1943. doi: 10.3969/j.issn.1004-731X.2004.09.025Yue Li, Yan Jun, Zhong Qiuhai. Simulations of debris impacts using three different algorithms[J]. Journal of System Simulation, 2004, 16(9):1941-1943. doi: 10.3969/j.issn.1004-731X.2004.09.025 [5] 王吉, 王肖钧, 卞梁.光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用[J].爆炸与冲击, 2007, 27(6):522-528. doi: 10.3321/j.issn:1001-1455.2007.06.007Wang Ji, Wang Xiaojun, Bian Liang. Linking of smoothed particle hydrodynamics method to standard finite element method and its application in impact dynamics[J]. Explosion and Shock Waves, 2007, 27(6):522-528. doi: 10.3321/j.issn:1001-1455.2007.06.007 [6] Attaway S W, Heinstein M W, Swegle J W. Coupling of Smooth particle hydrodynamic with finite element method[J]. Nuclear Engineering and Design, 1994, 150(2/3):199-205. doi: 10.1016-0029-5493(94)90136-8/ [7] De Vuyst T, Vignjevic R, Campbell J C. Coupling between meshless and finite element methods[J]. International Journal of Impact Engineering, 2005, 31(8):1054-1064. doi: 10.1016/j.ijimpeng.2004.04.017 [8] Xiao Y H, Han X, Hu D A. A coupling algorithm of finite element method and smoothed particle hydrodynamics for impact computations[J]. Computers, Materials & Continua, 2011, 23(1):9-34. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=a07c4b8549c5a92ea69f8ba69e561219 [9] 肖毅华, 胡德安, 韩旭, 等.一种自适应轴对称FEM-SPH耦合算法及其在高速冲击模拟中的应用[J].爆炸与冲击, 2012, 32(4):384-392. doi: 10.3969/j.issn.1001-1455.2012.04.007Xiao Yihua, Hu Dean, Han Xu, et al. An adaptive axisymmetric FEM-SPH coupling algorithm and its application to high velocity impact simulation[J]. Explosive and Shock Waves, 2012, 32(4):384-392. doi: 10.3969/j.issn.1001-1455.2012.04.007 [10] 宋太阳.冲击起爆弹丸对薄板侵彻过程研究[J].弹道学报, 1999, 11(4):54-69. http://www.cnki.com.cn/Article/CJFDTOTAL-DDXB199904012.htmSong Taiyang. Theinvestigation on penetration process of projectile initiated by impact onto thin-sheet[J]. Journal of Ballistics, 1999, 11(4):54-69. http://www.cnki.com.cn/Article/CJFDTOTAL-DDXB199904012.htm -






 下载:
下载: