On vibration reduction effect of short millisecond blasting by high-precision detonator based on HHT energy spectrum
-
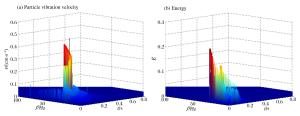
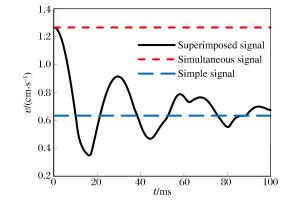
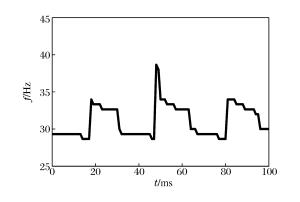
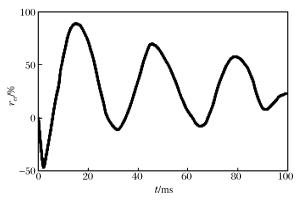
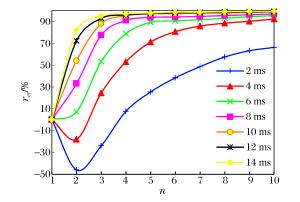
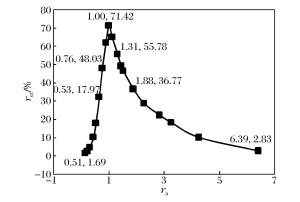
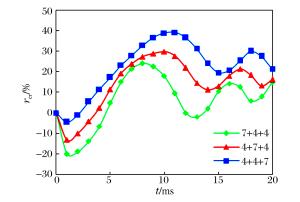
摘要: 为揭示高精度雷管短微差爆破干扰降振机理，选取紫金山金铜矿露天爆破实测的单段波形信号，利用Matlab分析了不同微差间隔下两段叠加信号的时频特征; 综合考虑爆破振动三要素并结合HHT(Hilbert-Huang transform)能量定义降能率，分析了段数、相邻振幅比和最大段药量位置对短微差爆破叠加信号降振效果的影响。根据研究成果，爆破设计时应避免出现前后段数药量差距过大，并尽量将较大药量的段数靠后起爆。研究表明：相同微差间隔下随着段数的增加，叠加信号降能率逐渐增大，当段数达到一定数量后增加分段数，微差爆破的降振效果并不明显; 微差爆破中相邻振幅比越接近1，降振效果越明显; 最大段药量靠后的叠加信号降能率大于其他顺序。Abstract: In order to reveal the mechanism of the interference vibration reduction of the short millisecond blasting of a high-precision detonator, on-site measured single-stage blasting vibration signals were selected to study the time frequency characteristics of the superposed signals in different millisecond intervals using the Matlab program. Comprehensively considering the three elements of the blasting vibration, energy reduction ratio and amplitude ratio were defined based on the HHT energy spectrum to study the influence of the segments, explosive charge ratio and vibration velocity proportion on the vibration reduction effect of the short millisecond blasting. The results show that an extremely big explosive charge ratio nearby should be avoided in the design of the millisecond blasting, and it would be better for a segment with a bigger explosive charge to have a posterior ignition. The research also shows that the energy reduction ratio increases with that of the segments in the same millisecond interval; the energy reduction ratio exhibits little obvious increases with that of the segments after the segments increase to a certain degree; the more similar the vibration characteristics of the two signals are to each other, the more evident the energy reduction effect; the energy reduction ratio of the superposed signals with a posterior vibration velocity proportion is more than the other orders.
-
图 1 单段爆破质点振动速度-时间曲线
Figure 1. Particle vibration velocity-time curve of single-stage blasting
图 2 单段爆破振动信号的HHT时频谱
Figure 2. HHT time-frequency spectra of single-stage blasting signal
图 3 不同微差间隔下叠加信号的峰值质点振动速度的变化
Figure 3. Peak particle velocity variations of superimposed signals at different millisecond delay intervals
图 4 不同微差间隔下叠加信号的主频变化
Figure 4. Main frequency variation of superimposed signal at different millisecond delay intervals
图 5 不同微差间隔下叠加信号的降能率
Figure 5. Energy reduction ratios ofsuperimposed signal at different millisecond delay intervals
图 6 短微差间隔下降能率随段数的变化关系
Figure 6. Change of energy reduction ratio with segmentsat short millisecond delay intervals
图 8 Blasting vibration monitoring data
Figure 8. Change of energy reduction ratio with time at different segment positions with the maximum charge
表 1 爆破振动监测数据
Table 1. Blasting vibration monitoring data
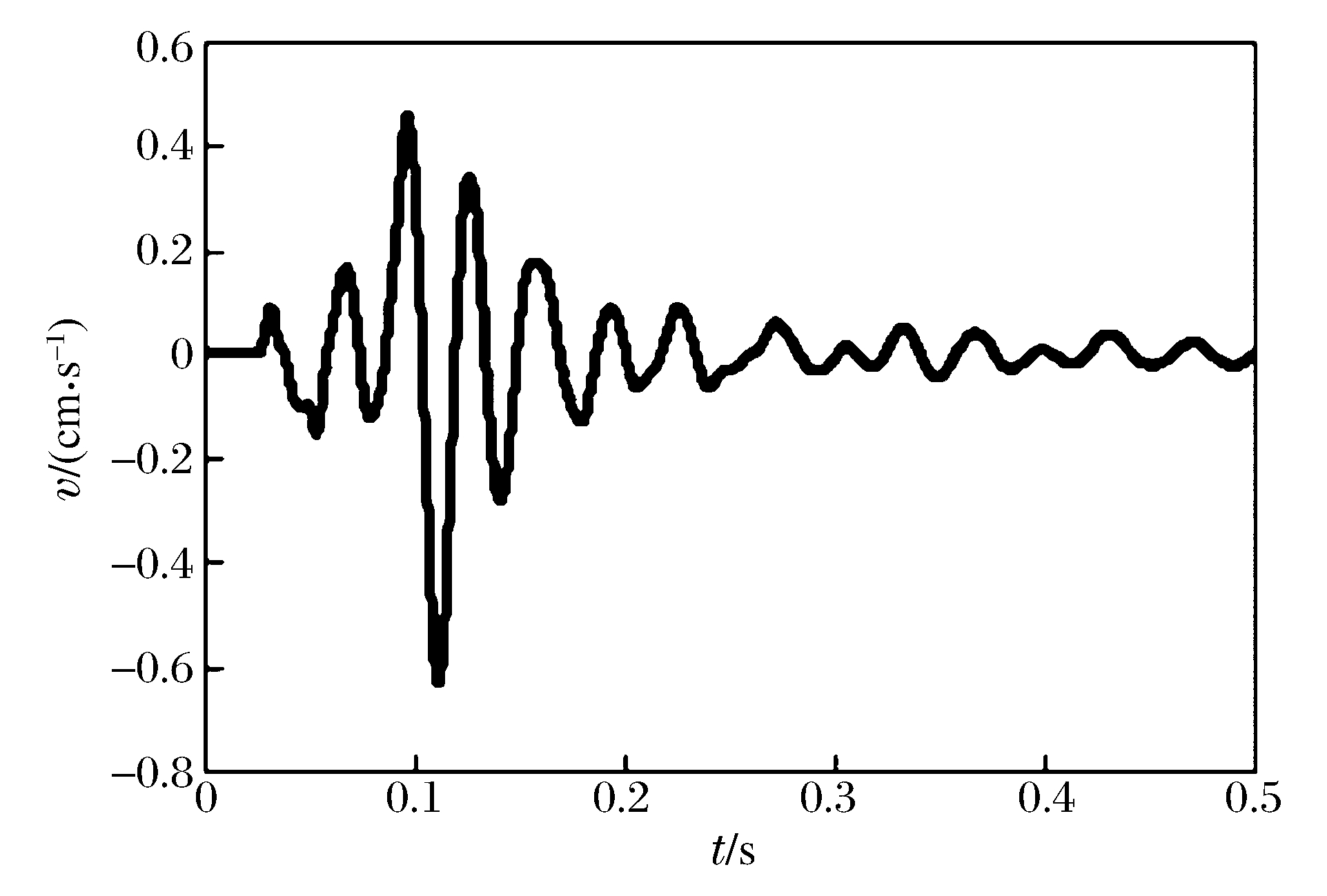
编号 药量/kg 高差/m 水平距离/m 质点振动速度峰值/(cm·s-1) 主频/Hz 持续时间/s 1 86 12 120 0.229 1 19.61 0.221 2 117 12 120 0.343 9 40.82 0.180 3 156 12 120 0.450 4 15.63 0.269 4 184 12 120 0.648 4 13.67 0.224 5 210 12 120 0.722 9 24.92 0.283 6 283 12 120 0.962 2 16.74 0.309 7 320 12 120 1.464 1 11.96 0.285 
下载: 导出CSV
-
[1] 张雪亮, 黄树棠.爆破地震效应[M].北京:地震出版社, 1981. [2] 宋光明, 曾新吾, 陈寿如, 等.基于波形预测小波包分析模型的降振微差时间选择[J].爆炸与冲击, 2003, 23(2):163-168. doi: 10.3321/j.issn:1001-1455.2003.02.012Song Guangming, Zeng Xinwu, Chen Shouru, et al. The selection of millisecond delay interval of blasting for decreasing ground vibration based on the wavelet packets prediction model of waveforms[J]. Explosion and Shock Waves, 2003, 23(2):163-168. doi: 10.3321/j.issn:1001-1455.2003.02.012 [3] 赵明生, 张建华, 易长平.基于单段波形叠加的爆破振动信号时频分析[J].煤炭学报, 2010, 35(8):1279-1282. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201001932637Zhao Mingsheng, Zhang Jianhua, Yi Changping. Time-frequency analysis based on single-stage addition of waveforms of blasting vibration signals[J]. Journal of China Coal Society, 2010, 35(8):1279-1282. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201001932637 [4] 赵明生, 梁开水, 余德运, 等.段数对爆破振动信号的时频特征影响分析[J].煤炭学报, 2012, 37(1):55-61. http://cdmd.cnki.com.cn/Article/CDMD-10497-1012442432.htmZhao Mingsheng, Liang Kaishui, Yu Deyun, et al. Effect of segments on time-frequency characteristics of blasting vibration signal[J]. Journal of China Coal Society, 2012, 37(1):55-61. http://cdmd.cnki.com.cn/Article/CDMD-10497-1012442432.htm [5] 陈士海, 燕永峰, 戚桂峰, 等.微差爆破降震效果影响因素分析[J].岩土力学, 2011, 32(10):3003-3008. doi: 10.3969/j.issn.1000-7598.2011.10.018Chen Shihai, Yan Yongfeng, Qi Guifeng, et al. Analysis of influence factors of interference vibration reduction of millisecond blasting[J]. Rock and Soil Mechanics, 2011, 32(10):3003-3008. doi: 10.3969/j.issn.1000-7598.2011.10.018 [6] 李夕兵, 凌同华.单段与多段微差爆破地震的反应谱特征分析[J].岩石力学与工程学报, 2005, 24(14):2409-2413. doi: 10.3321/j.issn:1000-6915.2005.14.002Li Xibing, Ling Tonghua. Response spectrum analysis of ground vibration induced by single deck and mlti-deck blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14):2409-2413. doi: 10.3321/j.issn:1000-6915.2005.14.002 [7] 李顺波, 杨军, 陈浦, 等.精确延时控制爆破振动的实验研究[J].爆炸与冲击, 2013, 33(5):513-518. doi: 10.3969/j.issn.1001-1455.2013.05.010Li Shunbo, Yan Jun, Chen Pu, et al. Experimental study of blasting vibration with precisely-controlled delay time[J]. Explosion and Shock Waves, 2013, 33(5):513-518. doi: 10.3969/j.issn.1001-1455.2013.05.010 [8] 王鹏.可编程电子延期雷管研究[D].武汉: 武汉理工大学, 2007: 10-25. http://cdmd.cnki.com.cn/Article/CDMD-10497-2007148973.htm [9] 徐振洋, 杨军, 陈占扬.高精度雷管逐孔起爆地震信号的精确时频分析[J].煤炭学报, 2013, 38(增2):331-336. http://d.old.wanfangdata.com.cn/Periodical/mtxb2013z2012Xu Zhenyang, Yang Jun, Chen Zhanyang. Precise time frequency analysis on seismic signal by hole initiation using high precision detonators[J]. Journal of China Coal Society, 2013, 38(Suppl 2):331-336. http://d.old.wanfangdata.com.cn/Periodical/mtxb2013z2012 [10] 马晓明, 王振宇, 陈银鲁, 等.精确微差爆破震动能量分布特征分析[J].解放军理工大学学报(自然科学版), 2012, 13(4):449-454. http://d.old.wanfangdata.com.cn/Periodical/jfjlgdxxb201204018Ma Xiaoming, Wang Zhenyu, Chen Yinlu, et al. Analysis of energy distribution of accurate millisecond blasting vibration[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2012, 13(4):449-454. http://d.old.wanfangdata.com.cn/Periodical/jfjlgdxxb201204018 [11] 李夕兵, 凌同华, 张义平.爆破振动信号分析理论与技[M].北京:科学出版社, 2009:99-100. [12] 张义平, 李夕兵, 左宇军.爆破振动信号的HHT分析与应用[M].北京:冶金工业出版社, 2009:32-42. [13] 孙新建.基于Hilbert能量分析的岩体爆破震动损伤研究[D].天津: 天津大学, 2012: 39-51. http://cdmd.cnki.com.cn/Article/CDMD-10056-1013004943.htm [14] Battista B M, Knapp C, Mcgee T, et al. Application of the empirical mode decomposition and Hilbert-Huang transform to seismic reflection data[J]. Geophysics, 2007, 72(2):29-37. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=GPYSA7000072000002000H29000001&idtype=cvips&gifs=Yes [15] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971):903-995. doi: 10.1098/rspa.1998.0193 [16] 徐国元, 中国生, 熊正明.基于小波变换的爆破地震安全能量分析法的应用研究[J].岩土工程学报, 2006, 28(1):24-28. doi: 10.3321/j.issn:1000-4548.2006.01.004Xu Guoyuan, Zhong Guosheng, Xiong Zhengming. Study and application of energy analysis method for blasting seismic safety based on wavelet transform[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(1):24-28. doi: 10.3321/j.issn:1000-4548.2006.01.004 [17] 王振宇, 梁旭, 陈银鲁, 等.基于输入能量的爆破振动安全评价方法研究[J].岩石力学与工程学报, 2010, 29(12):2492-2499. http://www.cnki.com.cn/Article/CJFDTotal-YSLX201012018.htmWang Zhenyu, Liang Xu, Chen Yinlu, et al. Study of safety evaluation method of blasting vibration based on input energy[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12):2492-2499. http://www.cnki.com.cn/Article/CJFDTotal-YSLX201012018.htm [18] Yang J N, Lei Y, Lin S, et al. Hilbert-Huang based approach for structural damage detection[J]. Journal of Engineering Mechanic, 2004, 130(1):85-95. doi: 10.1061/(ASCE)0733-9399(2004)130:1(85) [19] 凌同华.爆破震动效应及其灾害的主动控制[D].长沙: 中南大学, 2004: 34-52. http://cdmd.cnki.com.cn/Article/CDMD-10533-2004116227.htm [20] 唐跃, 曹跃, 罗明荣, 等.高精度数码雷管在爆破施工降振中的应用[J].爆破, 2011, 28(1):107-110. doi: 10.3963/j.issn.1001-487X.2011.01.030Tan Yue, Cao Yue, Luo Mingrong, et al. Application of high-precision electronic detonator in decreasing blasting vibration[J]. Blasting, 2011, 28(1):107-110. doi: 10.3963/j.issn.1001-487X.2011.01.030 [21] 赵明生, 梁开水, 曹跃, 等.爆破地震作用下建(构)筑物安全标准探讨[J].爆破, 2008, 25(4):24-27. http://d.old.wanfangdata.com.cn/Periodical/bp200804007Zhao Mingsheng, Liang Kaishui, Cao Yue, et al. Discussion on the security criteria of construction (structure) of building under blasting vibration[J]. Blasting, 2008, 25(4):24-27. http://d.old.wanfangdata.com.cn/Periodical/bp200804007 [22] 李宝山, 张义平.HHT能量判别法在英坪矿爆破振动中的应用[J].工程爆破, 2013, 19(6):13-17. doi: 10.3969/j.issn.1006-7051.2013.06.004Li Baoshan, Zhang Yiping. The application of HHT energy discrimination in blasting vibration of Ying-ping mine[J]. Engineering Blasting, 2013, 19(6):13-17. doi: 10.3969/j.issn.1006-7051.2013.06.004 -
点击查看大图
图(8) / 表(1)
计量
- 文章访问数: 4766
- HTML全文浏览量: 1654
- PDF下载量: 432
- 被引次数: 0