Numerical studies of sinusoidally premixed flame interface instability induced by multiple shock waves
-
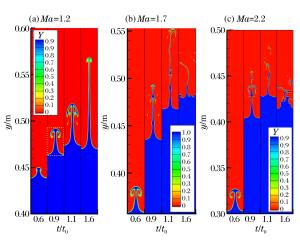
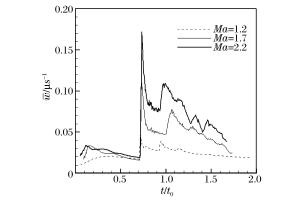
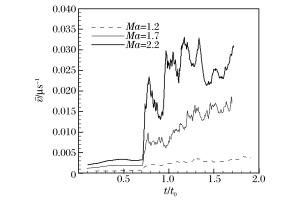
摘要: 激波诱导火焰失稳是实际中常见的现象，为深入研究火焰失稳特性，采用三维单步化学反应的Navier-Stokes方程和9阶weighted essentially non-oscillatory (WENO)的高精度格式，对不同马赫数的入射激波及其反射激波多次诱导正弦型预混火焰界面失稳的现象进行了三维数值模拟，并对计算结果的可靠性进行了验证。研究结果显示，在激波的多次作用下，火焰界面的演变过程主要受Richtmyer-Meshkov (RM)不稳定特性和化学反应特性的双重影响，且随着入射激波强度的增强，上述2种特性均得到进一步强化。为构造体现反应性RM不稳定特性的参数，根据火焰界面混合区平均涡量和化学反应速率，提出了表征界面受不稳定性和化学反应影响的量纲一参数。通过分析发现，在同一入射激波强度下，该参数的对数形式随入射激波和反射激波的多次作用呈基本相同的线性增长趋势；对不同马赫数的入射激波，该参数对数形式的线性增长率也基本一致。这样的变化表明该量纲一参数能够反映反应性RM不稳定过程中火焰界面发展的内在规律。Abstract: In this work, to further study the features of the shock-wave induced flame instability, the two-dimensional Navier-Stokes (NS) equations with the single-step chemical reaction and the high resolution 9th-order weighted essentially non-oscillatory (WENO) scheme were adopted to simulate the instability of the sinusoidally premixed flame induced by incident shock waves with different Mach numbers and its reshock waves. The computational results were validated by the experimental results in the related literature. The computational results show that the evolutions of the flame are mainly influenced by both the Richtmyer-Meshkov (RM) instability and the chemical reaction. With the growth of the incident shock wave intensity, the interface instability and the chemical reaction are enhanced. To construct the parameter that can characterize the RM instability in the reactive flow, a dimensionless parameter 8338A131 that describes the interface RM instability and the chemical reactivity was proposed based on the average vorticity and the chemical reaction rate calculated in the mixing zone of the flame interface. The analysis of the parameter shows that, with the similar intensity of the incident shock wave, the logarithmic form of the parameter exhibits basically the same linear growth when an incident shock wave with a given Mach number and its reshocks successively pass through the flame interface. The linear growth rate of the logarithmic form of the parameter is also basically the same for different Mach numbers of the incident wave. Such variations of η suggest that the dimensionless parameter proposed in the present study can well characterize the intrinsic features of the flame interface development in the reactive RM instability process.
-
Key words:
- shock wave /
- flame instability /
- WENO /
- Richtmyer-Meshkov instability /
- chemical reaction
-
图 4 不同时刻的涡量和化学反应放热率分布(Ma=2.2)
Figure 4. Distributions of vorticity and heat release rate of chemical reaction at different times (Ma=2.2)
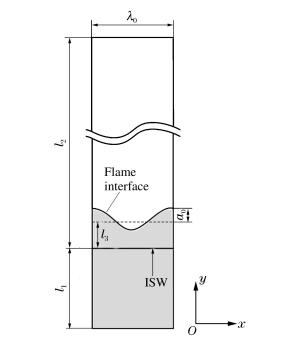
表 1 计算区域尺寸
Table 1. Size of computational domain
Ma l1/m l2/m l3/m λ0/m 1.2 0.4 0.2 0.01 0.02 1.7 0.1 0.5 0.01 0.02 2.2 0.01 0.5 0.01 0.02 
下载: 导出CSV
表 2 η的拟合参数
Table 2. Fitting perameters of η
Ma A1 A2 R2 1.2 1.268 -4.020 0.9150 1.7 1.465 -3.256 0.9179 2.2 1.323 -2.703 0.9082
下载: 导出CSV
-
[1] Marble F E, Sonneborn G, Pun C S J, et al. Physic conditions in circumstellar gas surrounding SN 1987A 12 years after outburst[J]. The Astrophysical Journal, 2000, 545:390-398. doi: 10.1086/apj.2000.545.issue-1 [2] Oran E S, Gamezo V N. Origins of the deflagration-to-detonation transition in gas-phrase combustion[J]. Combustion Flame, 2007, 148(1-2):4-47. doi: 10.1016/j.combustflame.2006.07.010 [3] Yang J, Kubota T, Zukoski E E. Applications of shock-induced mixing to supersonic combustion[J]. AIAA Journal, 1993, 31(5):854-862. doi: 10.2514/3.11696 [4] Markstein G H. A shock-tube study of flame front-pressure wave interaction[C]//6th Symposium (International) on Combustion. Pittsburgh, USA: The Combustion Institute, 1957: 387-398. [5] Ton V T, Karagozian A R, Marble F F, et al. Numerical simulations of high speed chemically reactive flow[J]. Theoretical and Computational Fluid Dynamics, 1994, 6:161-179. doi: 10.1007/BF00312347 [6] Ju Y, Shimano A, Inoue O. Vorticity generation and flame distortion induced by shock flame interaction[C]//27th Symposium (International) on Combustion. Pittsburgh. USA: The Combustion Institute, 1998: 735-741. [7] 朱跃进, 董刚, 刘怡昕, 等.激波诱导火焰变形、混合和燃烧的数值研究[J].爆炸与冲击, 2013, 33(4):430-437. doi: 10.3969/j.issn.1001-1455.2013.04.016Zhu Yuejin, Dong Gang, Liu Yixin, et al. A numerical study on shock induced distortion, mixing and combustion of flame[J]. Explosion and Shock Waves, 2013, 33(4):430-437. doi: 10.3969/j.issn.1001-1455.2013.04.016 [8] Zhu Yuejin, Dong Gang, Liu Yixin, et al. Three-dimensional numerical simulations of spherical flame evolutions in shock reshock accelerate flows[J]. Combustion Science and Technology, 2013, 185(10):1415-1440. doi: 10.1080/00102202.2013.798656 [9] Khokhlov A M, Oran E S, Chtchelkanova A Y. Interaction of a shock with a sinusoidally perturbed flame[J]. Combustion and Flame, 1999, 117:99-116. doi: 10.1016/S0010-2180(98)00090-X [10] Kilchyk V, Nalim R, Merkle C. Laminar premixed flame fuel consumption rate modulation by shocks and expansion waves[J]. Combustion and Flame, 2011, 158:1140-1148. doi: 10.1016/j.combustflame.2010.10.026 [11] Massa L, Jha P. Linear analysis of the Richtmyer-Meshkov instability in shock-flame interactions[J]. Physics of Fluids, 2012, 24:056101. doi: 10.1063/1.4719153 [12] Leinov E, Malamud G, Elbaz Y, et al. Experimental and numerical investigation of the Richtmyer-Meshkov instability under re-shock conditions[J]. Fluid Mechanics, 2009, 626:449-475. doi: 10.1017/S0022112009005904 [13] Ukai S, Balakrishnan K, Menon S. Growth rate predictions of single- multi-mode Richtmyer-Meshkov instability with reshock[J]. Shock Wave, 2011, 21:533-546. doi: 10.1007/s00193-011-0332-0 [14] Balsara D S, Shu C W. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy[J]. Journal of Computational Physics, 2000, 160:405-452. doi: 10.1006/jcph.2000.6443 [15] Thomas G O, Bambrey R, Brown C. Experimental observations of flame acceleration and transition to detonation following shock-flame interaction[J]. Combustion Theory and Modelling, 2001, 5(4):573-594. doi: 10.1088/1364-7830/5/4/304 [16] 蒋华, 董刚, 陈霄, 小扰动界面形态对RM不稳定性影响的数值分析[J].力学学报, 2014, 46(4):544-552. doi: 10.7638/kqdlxxb-2013.0008Jiang Hua, Dong Gang, Chen Xiao. Numerrical study on the effects of small amplitude initial perturbations on RM instability[J]. Chinese Jounal of Theoretical and Applied Mechanics, 2014, 46(4):544-552. doi: 10.7638/kqdlxxb-2013.0008 [17] Latini M, Schilling O, Don W S. Effects of WENO flux reconstruction order and spatial resolution on reshocked two-dimensional Richtmyer-Meshkov instability[J]. Journal of Computational Physics, 2007, 221:805-836. doi: 10.1016/j.jcp.2006.06.051 -
点击查看大图
图(7) / 表(2)
计量
- 文章访问数: 4279
- HTML全文浏览量: 1411
- PDF下载量: 330
- 被引次数: 0