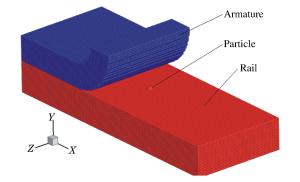
3D numerical research of railgun gouging mechanism based on material point method
-
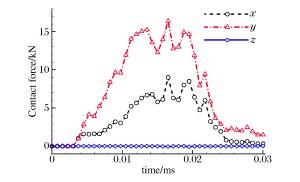
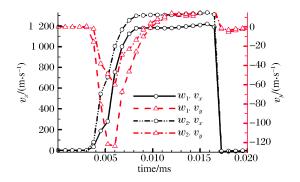
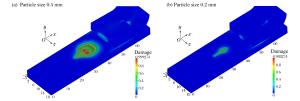
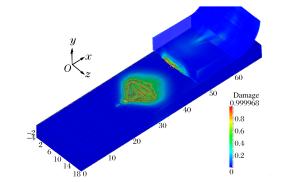
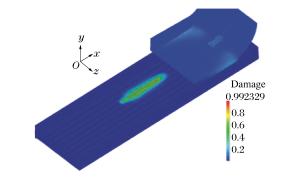
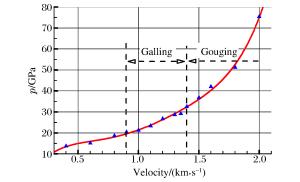
摘要: 基于轨道炮结构特点以及冲击热力学理论，采用物质点法建立了轨道微颗粒诱发刨削的三维模型，模拟了轨道刨削的形成过程，并对其产生机理与影响因素进行了分析。结果表明：电枢与轨道的局域高速冲击产生瞬时的能量交换，形成的高热高压金属流对轨道表面的斜侵彻作用形成了刨坑；刨削的产生存在速度阈值，超过速度阈值，随着电枢速度增加，刨削越严重；低于速度阈值，可产生轨道擦伤；减小轨道表面微颗粒尺寸、增加电枢头部倾角均可降低刨削损伤。Abstract: Based on the structural features of the railgun and the theories of impact thermodynamics, a 3D gouging model containing a micro particle was established using the material point method to simulate the formation process of the rail gouging, and the gouging mechanism and some influencing factors were also analyzed. The results show that the local impact between the armature and the rails at a high velocity produces transient energy exchanges, thus simultaneously forming metal flows with high energy and high pressure that penetrate obliquely into the rail and cause the formation of gouging, for which there is a threshold velocity to produce. As the armature velocity increases, the gouging damage gets more serious. On the other hand, the galling damage occurs when the armature velocity is below the threshold velocity. Both controlling the particle size within a certain range and increasing the head angle of the armature will help to suppress the formation of gouging.
-
Key words:
- impact dynamics /
- material point method /
- railgun /
- gouging /
- hypervelocity
-
图 2 轨道刨削物质点法计算模型
Figure 2. A simulation model of railgun gouging constructed with material point method
图 3 轨道刨坑形成过程Mises应力云图
Figure 3. Mises stress distribution during the formation process of gouging
图 5 2个质点受冲击时的速度变化曲线
Figure 5. Velocities of two particles varying with time during impacting
图 6 1.5 km/s冲击速度下数值模拟出的泪滴状刨坑
Figure 6. Tear-drop gouge craters from numerical simulation at 1.5 km/s
表 1 电枢与轨道材料参数
Table 1. Material parameters of armature and rail
材料 ρ/(kg·m-3) E/GPa ν cp/(J·kg-1·K-1) A/MPa B/MPa n C m Tm/K Tr/K ${\dot \varepsilon }$0/s-1 χ D1 D2 D3 D4 D5 c0/(m·s-1) s γ0 7075铝 2 810 71 0.33 960 369 684 0.73 0.008 3 1.7 933 293 1 0.9 0.13 0.13 -1.5 0.011 0 5 350 1.34 2 无氧铜 8 960 124 0.34 383 90 292 0.31 0.025 1.09 1 356 293 1 0.9 0.54 4 2 0.014 1.12 3 940 1.49 2 
下载: 导出CSV
-
[1] 李军, 严萍, 袁伟群.电磁轨道炮发射技术的发展与现状[J].高电压技术, 2014, 40(4):1052-1064. http://d.old.wanfangdata.com.cn/Periodical/gdyjs201404014Li Jun, Yan Ping, Yuan Weiqun. Electromagnetic gun technology and it's development[J]. High Votage Engineering, 2014, 40(4):1052-1064. http://d.old.wanfangdata.com.cn/Periodical/gdyjs201404014 [2] Graff K F, Dettloff B B. The gouging phenomenon between metal surfaces at very high sliding speeds[J]. Wear, 1969, 14(2):87-97. doi: 10.1016/0043-1648(69)90339-1 [3] Cinnamon J D, Palazotto A N, Szmerekovsky A G. Further refinement and validation of material models for hypervelocity gouging impacts[J]. American Institute of Aeronautics and Astronautics, 2008, 46(2):317-327. doi: 10.2514/1.25035 [4] Stefani F, Parker J V. Experiments to measure gouging threshold velocity for various metals against copper[J]. IEEE Transactions on Magnetics, 1999, 35(1):312-316. doi: 10.1109/20.738423 [5] Persad C, Prabhu G, White G, et al. Characterization of hypervelocity gouge craters in rail conductors[J]. IEEE Transactions on Magnetics, 1997, 33(1):401-405. doi: 10.1109/20.560045 [6] Watt T J, Clay C E, Bassett P M, et al. The effect of surface indentations on gouging in railguns[J]. Wear, 2014, 310(1/2):41-50. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=266be5121f733b3a9b099eab65c32ced [7] Barber J P, Bauer D P, Ahmadi R. Contact phenomena at hypervelocities[J]. Wear, 1982, 78(1/2):163-169. doi: 10.1016-0043-1648(82)90028-X/ [8] Barker L M, Trucano T G, Susoeff A R. Railgun rail gouging by hypervelocity sliding contact[J]. IEEE Transactions on Magnetics, 1989, 25(1):83-87. doi: 10.1109/20.22510 [9] 金龙文, 雷彬, 李治源, 等.轨道炮刨削形成机理分析及数值模拟[J].爆炸与冲击, 2013, 33(5):537-543. doi: 10.3969/j.issn.1001-1455.2013.05.014Jin Longwen, Lei Bin, Li Zhiyuan, et al. Formation mechanism analysis and numerical simulation of railgun gouging[J]. Explosion and Shock Waves, 2013, 33(5):537-543. doi: 10.3969/j.issn.1001-1455.2013.05.014 [10] Barker L M, Trucano T G, Susoeff A R. Gun barrel gouging by sliding metal contact at very high velocities[J]. IEEE Transactions on Magnetics, 1989, 1(25):83-87. [11] Bourell D L, Persad C. Simulation of railgun gouging[J]. IEEE Transactions on Magnetics, 1999, 35(1):274-276. doi: 10.1109/20.738416 [12] Zhu Rengui, Zhang Qian, Li Zhiyuan, et al. Impact physics model and influencing factors of gouging for electromagnetic rail launcher[C]//17th International Symposium on Electromagnetic Launch Technology. La Jolla, California, USA, 2014. [13] 刘峰, 赵丽曼, 张晖辉, 等.电磁轨道炮刨削的形成机理及仿真分析[J].高压物理学报, 2015, 29(3):199-205. http://www.cqvip.com/QK/96553X/201503/71898776504849534851484854.htmlLiu Feng, Zhao Liman, Zhang Huihui, et al. Formation mechanism and simulation analysis of railgun gouging[J]. Chinese Journal of High Pressure Physics, 2015, 29(3):199-205. http://www.cqvip.com/QK/96553X/201503/71898776504849534851484854.html [14] 廉艳平, 张帆, 刘岩, 等.物质点法的理论和应用[J].力学进展, 2013, 43(2):237-264. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20132013052800030339Lian Yanping, Zhang Xiong, Liu Yan, et al. Material point method and its applications[J]. Advances in Mechanics, 2013, 43(2):237-264. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20132013052800030339 [15] 张雄, 廉艳平, 刘岩, 等.物质点法[M].北京:清华大学出版社, 2013:7-13.Zhang Xiong, Lian Yanping, Liu Yan, et al. Material point method[M]. Beijing: Tsinghua University Press, 2013:7-13. -
图(10) / 表(1)
计量
- 文章访问数: 4474
- HTML全文浏览量: 1276
- PDF下载量: 400
- 被引次数: 0