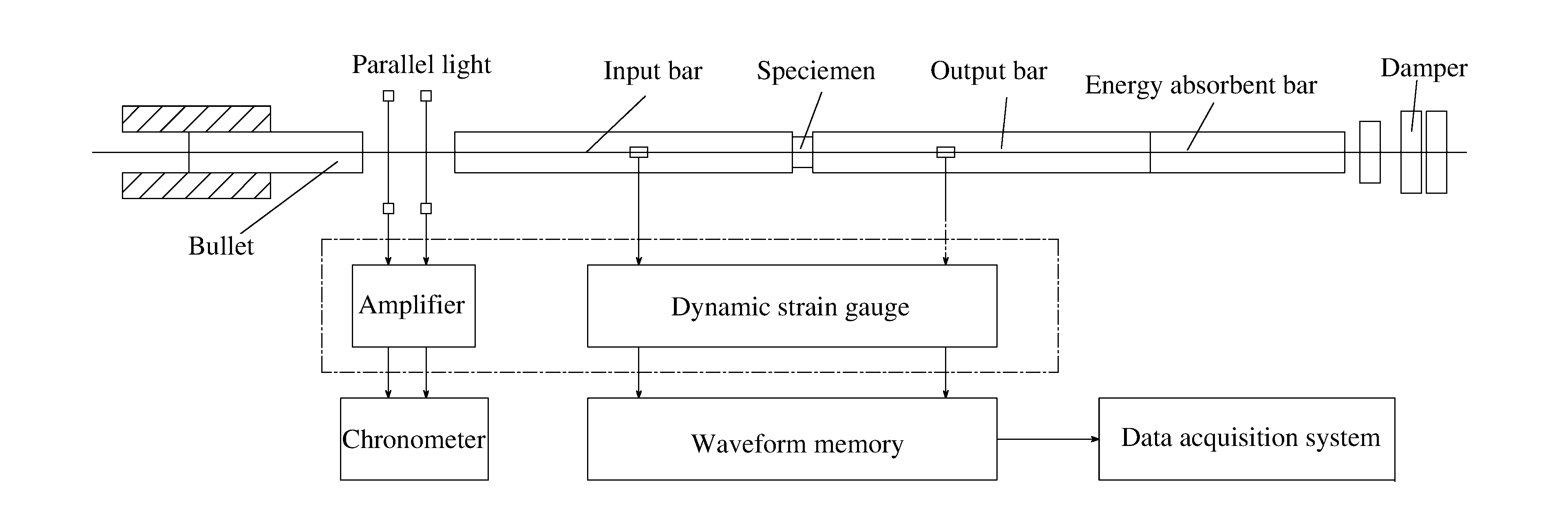
Mechanical properties of reactive powder concrete-filled steel tube after exposure to high temperature under impact loading
-
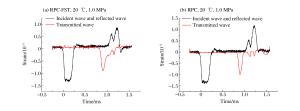
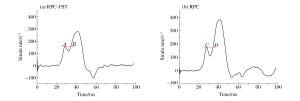
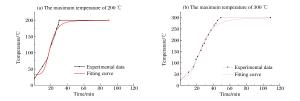
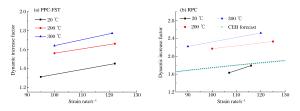
摘要: 采用霍普金森压杆装置对高温后钢管活性粉末混凝土(reactive powder concrete-filled steel tube,RPC-FST)进行冲击压缩实验,分析了应变率效应及温度效应对试件动态力学性能的影响。结果表明:高温(200、300 ℃)后RPC-FST仍具有较好的抗冲击能力、延性和完整性;冲击荷载作用下,RPC-FST的应变率效应明显弱于RPC的应变率效应;随着过火温度的提高,RPC-FST的峰值应力逐渐增大,变形能力增强,抗冲击能力提高。动力提高系数随过火温度的提高而增大,说明高温后RPC-FST的应变率效应更显著。Abstract: Experiments on reactive powder concrete-filled steel tube (RPC-FST) specimens after exposure to high temperature were performed by using a split Hopkinson pressure bar (SHPB) apparatus, and the influences of strain rate effects and temperature effects on the dynamic behaviors of RPC-FST were investigated. Test results show that the RPC-FST specimens after exposure to high temperature have excellent impact-resistance, ductility and integrity. The strain rate effects of the RPC-FST specimens are weaker than those of the RPC specimens under impact loading. The peak stress of the RPC-FST specimens increases as the temperature increases, and the deformation capability and impact-resistance increase. The dynamic increase factor (DIF) increases as the temperature increases. It means that the strain rate effects of RPC-FST become more obvious after exposure to high temperature.
-
表 1 RPC-FST冲击实验结果
Table 1. Experimental results of RPC-FST specimens under impact loading
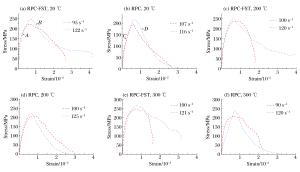
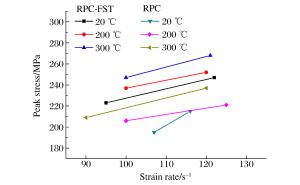
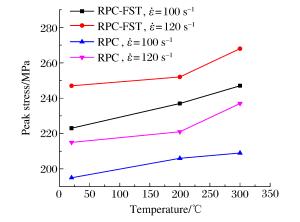
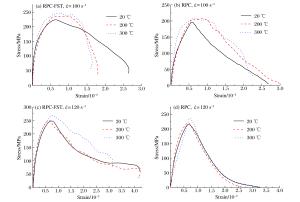
编号 θmax/℃ p0/MPa v0/(m·s-1) σp/MPa σp/MPa ${\mathit{\bar{\dot{\varepsilon }}}}$/s-1 λdi s0b 20 0.8 12.1 218~227 223 95 1.31 s0c 20 1.0 14.3 242~250 247 122 1.45 s1b 200 0.8 12.3 235~240 237 100 1.56 s1c 200 1.0 14.0 249~255 252 122 1.66 s2b 300 0.8 12.2 245~250 247 100 1.64 s2c 300 1.0 14.1 265~272 268 121 1.77 表 2 RPC冲击实验结果
Table 2. Experimental results of RPC specimens under impact loading
编号 θmax/℃ p0/MPa v0/(m·s-1) σp/MPa σp/MPa ${\mathit{\bar{\dot{\varepsilon }}}}$/s-1 λdi s0b 20 0.8 12.0 192~200 195 107 1.63 s0c 20 1.0 14.1 211~220 215 116 1.79 s1b 200 0.8 12.1 204~207 206 100 2.17 s1c 200 1.0 14.2 219~224 221 125 2.33 s2b 300 0.8 12.0 205~214 209 90 2.22 s2c 300 1.0 14.2 231~241 237 120 2.52 表 3 动力提高系数的理论值与实验值的对比
Table 3. Comparisons of experimental and analytical dynamic increase factors
编号 θmax/℃ p0/MPa 平均应变率/s-1 动力提高系数 实验值 理论值 相对误差/% s0b 20 0.8 95 1.31 1.30 -0.9 s0c 20 1.0 122 1.45 1.36 -6.1 s1b 200 0.8 100 1.56 1.74 11.4 s1c 200 1.0 120 1.66 1.80 8.3 s2b 300 0.8 100 1.64 1.75 6.9 s2c 300 1.0 121 1.77 1.81 1.9 -
[1] Tian Zhimin, Wu Ping'an, Jia Jianwei. Dynamic response of RPC-filled steel tubular columns with high load carrying capacity under axial impact loading[J]. Transactions of Tianjin University, 2008, 14(6):441-449. doi: 10.1007/s12209-008-0076-9 [2] Bambach M R. Design of hollow and concrete filled steel and stainless steel tubular columns for transverse impact loads[J]. Thin-Walled Structures, 2011, 49(10):1251-1260. doi: 10.1016/j.tws.2011.05.009 [3] Remennikov A M, Kong S Y, Uy B. Response of foam- and concrete-filled square steel tubes under low-velocity impact loading[J]. Journal of Performance of Constructed Facilities, 2011, 25(5):373-381. doi: 10.1061/(ASCE)CF.1943-5509.0000175 [4] Yousuf M, Uy B, Tao Z, et al. Transverse impact resistance of hollow and concrete filled stainless steel columns[J]. Journal of Constructional Steel Research, 2013, 82:177-189. doi: 10.1016/j.jcsr.2013.01.005 [5] Han Linhai, Hou Chuanchuan, Zhao Xiaoling, et al. Behaviour of high-strength concrete filled steel tubes under transverse impact loading[J]. Journal of Constructional Steel Research, 2014, 92(1):25-39. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=7f0b3eea375dbc763649c5047f08e777 [6] Wang Rui, Han Linhai, Hou Chuanchuan. Behavior of concrete filled steel tubular (CFST) members under lateral impact: Experiment and FEA model[J]. Journal of Constructional Steel Research, 2013, 80(1):188-201. http://www.sciencedirect.com/science/article/pii/S0143974X12002106 [7] 何远明, 霍静思, 陈柏生.高温下钢管混凝土SHPB动态力学性能试验研究[J].工程力学, 2013, 30(1):52-58. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20132013051500003654He Yuanming, Huo Jingsi, Chen Baisheng. Impact tests on dynamic behavior of concrete-filled steel tube at elevated temperatures[J]. Engineering Mechanics, 2013, 30(1):52-58. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QKC20132013051500003654 [8] 霍静思, 任晓虎, 肖岩.标准火灾作用下钢管混凝土短柱落锤动态冲击试验研究[J].土木工程学报, 2012, 45(4):9-20. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201200684144Huo Jingsi, Ren Xiaohu, Xiao Yan. Impact behavior of concrete-filled steel tubular stub columns under ISO-834 standard fire[J]. China Civil Engineering Journal, 2012, 45(4):9-20. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201200684144 [9] 霍静思, 何远明, 肖莉平, 等.高温后钢管混凝土抗多次冲击力学性能试验研究[J].湖南大学学报(自然科学版), 2012, 39(9):6-10. doi: 10.3969/j.issn.1674-2974.2012.09.002Huo Jingsi, He Yuanmin, Xiao Liping, et al. Experimental study on the dynamic behavior of concrete-filled steel tube after exposure to high temperatures under multiple impact loadings[J]. Journal of Hunan University (Natural Sciences), 2012, 39(9):6-10. doi: 10.3969/j.issn.1674-2974.2012.09.002 [10] 钟善桐.钢管混凝土结构[M].3版.北京:清华大学出版社, 2003:231-268. [11] Bischoff P H, Perry S H. Compressive behaviour of concrete at high strain rates[J]. Materials & Structures, 1991, 24(6):425-450. doi: 10.1007/BF02472016 [12] Davies E D H, Hunter S C. The dynamic compression testing of solids by the method of split Hopkinson pressure bar[J]. Journal of the Mechanics and Physics of Solids, 1963, 11(3):155-179. doi: 10.1016/0022-5096(63)90050-4 [13] 混凝土结构设计规范: GB50010-2002[S].北京: 中国建筑工业出版社, 2002: 13-15. [14] 金属材料室温拉伸试验方法: GB/T228-2002[S].北京: 中国建筑工业出版社, 2002: 10-12. [15] 王礼立.应力波基础[M].北京:国防工业出版社, 2010:5-35. [16] 李志武, 许金余, 白二雷, 等.高温后混凝土SHPB试验研究[J].振动与冲击, 2012, 31(8):143-147. doi: 10.3969/j.issn.1000-3835.2012.08.028Li Zhiwu, Xu Jinyu, Bai Erlei, et al. SHPB test for post-high-temperature concrete[J]. Journal of Vibration and Shock, 2012, 31(8):143-147. doi: 10.3969/j.issn.1000-3835.2012.08.028 [17] Song T Y. Concrete filled steel tube stub columns under combined temperature and loading[J]. Journal of Constructional Steel Research, 2010, 66(3):369-384. doi: 10.1016/j.jcsr.2009.10.010 [18] 林震宇, 吴炎海, 沈祖炎.圆钢管活性粉末混凝土轴压力学性能研究[J].建筑结构学报, 2005, 26(4):52-56. doi: 10.3321/j.issn:1000-6869.2005.04.008Lin Zhenyu, Wu Yanhai, Shen Zuyan. Research on behavior of RPC filled circular steel tube column subjected to axial compression[J]. Journal of Building Structures, 2005, 26(4):52-56. doi: 10.3321/j.issn:1000-6869.2005.04.008 [19] 李海艳.活性粉末混凝土高温爆裂及高温后力学性能研究[D].哈尔滨: 哈尔滨工业大学, 2012: 60, 96-97. [20] Comité Euro-International du Béton. Concrete structure under impact and impulsive loading: CEB Bulletin No.187[R]. Lausanne Switzerland, 1988. [21] 任晓虎, 霍静思, 陈柏生.高温后钢管混凝土短柱落锤动态冲击试验研究[J].振动与冲击, 2011, 30(11):67-73. doi: 10.3969/j.issn.1000-3835.2011.11.015Ren Xiaohu, Huo Jingsi, Chen Baisheng. Dynamic behaviors of concrete-filled steel stub columns after exposure to high temperature[J]. Journal of Vibration and Shock, 2011, 30(11):67-73. doi: 10.3969/j.issn.1000-3835.2011.11.015 [22] Xiao Yan, Shan Jianhua, Zheng Qiu, et al. Experimental studies on concrete filled steel tubes under high strain rate loading[J]. Journal of Materials in Civil Engineering, 2009, 21(10):569-577. doi: 10.1061/(ASCE)0899-1561(2009)21:10(569) [23] Jones N. Structural impact[M]. Cambridge, New York: Cambridge University Press, 1988:100-150. -






 下载:
下载: