时序控制预裂爆破参数优化及应用

叶海旺; 唐可; 万涛; 王超; 雷涛; 李新平; C.M.Saliou

doi:10.11883/1001-1455(2017)03-0502-08

时序控制预裂爆破参数优化及应用

doi: 10.11883/1001-1455(2017)03-0502-08

叶海旺^{1, 2},
唐可¹,
万涛¹,
王超¹,
雷涛^{1, 2, ,},
李新平³,
C.M.Saliou¹

1.
武汉理工大学资源与环境工程学院，湖北武汉 430070
2.
武汉理工大学矿物资源加工与环境湖北省重点实验室，湖北武汉 430070
3.
武汉理工大学土木与建筑工程学院，湖北武汉 430070

基金项目:

国家自然科学基金项目 51274157

中央高校基本科研业务费专项基金项目 2015IVA028

详细信息

作者简介:
叶海旺 (1971-)，男，博士，副教授

通讯作者:
雷涛，leitao539@163.com

中图分类号: O381
计量
- 文章访问数: 4543
- HTML全文浏览量: 1331
- PDF下载量: 499
- 被引次数: 0
出版历程
- 收稿日期: 2015-11-09
- 修回日期: 2016-04-11
- 刊出日期: 2017-05-25

Optimization of time sequence controlled pre-splitting blasting parameters and its application

Ye Haiwang^{1, 2},
Tang Ke¹,
Wan Tao¹,
Wang Chao¹,
Lei Tao^{1, 2
, ,},
Li Xinping³,
C.M. Saliou¹

1.
School of Resources and Environmental Engineering, Wuhan University of Technology, Wuhan 430070, Hubei, China
2.
Hubei Key Laboratory of Mineral Resources Processing and Environment, Wuhan University of Technology, Wuhan 430070, Hubei, China
3.
School of Civil Engineering and Architecture, Wuhan University of Technology, Wuhan 430070, Hubei, China

摘要

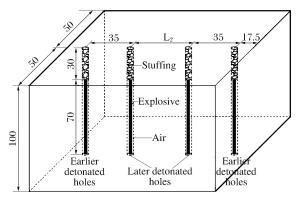
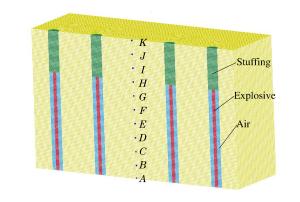
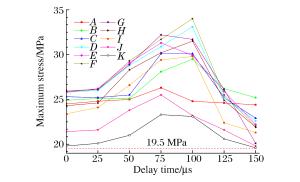
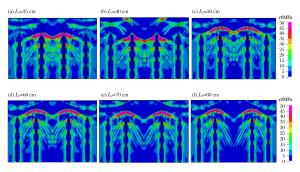
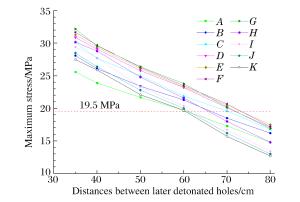
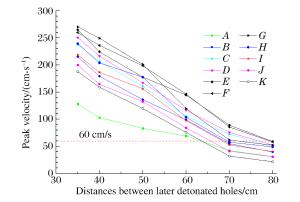
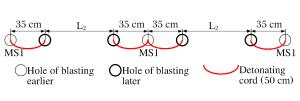
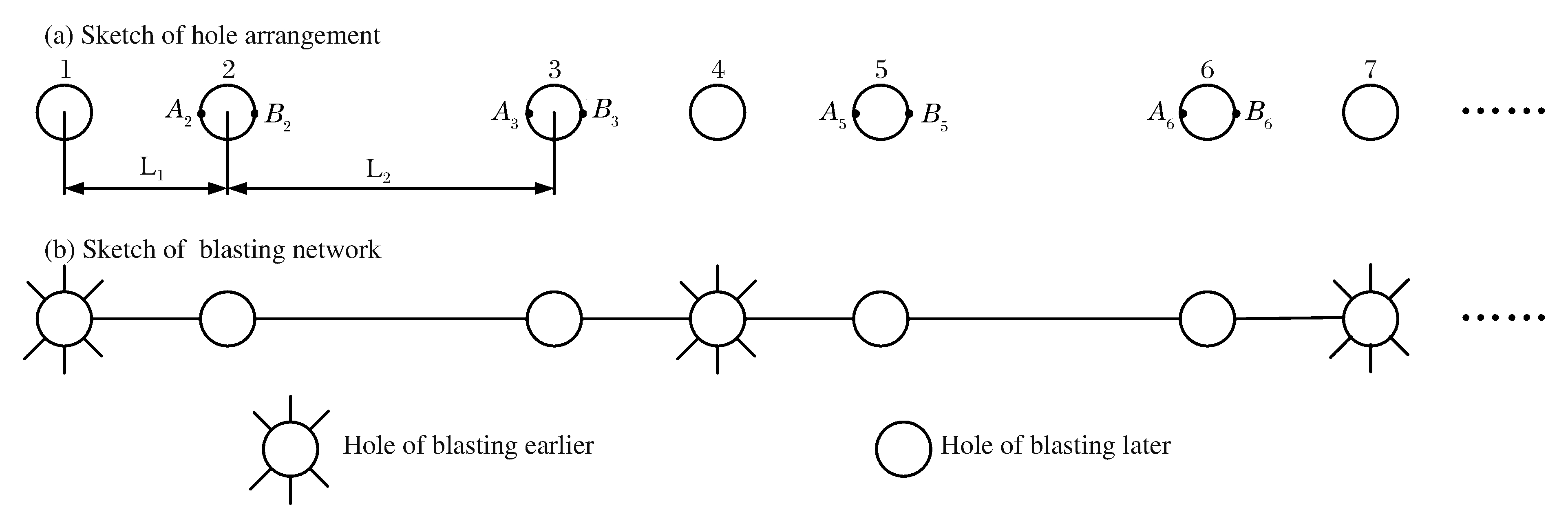
摘要: 针对白鹤滩水电站地下厂房的爆破开挖，为降低爆破对岩体的损伤，采用数值模拟与现场试验研究小孔径时序控制预裂爆破中，后爆孔孔间延期时间及后爆孔孔距对时序控制预裂爆破成缝的影响，从而获取合理的延期时间和最佳的后爆孔孔距。研究结果表明，孔径为42mm的时序控制预裂爆破，先爆孔孔距为35cm时，合理的起爆延期时间为75~100μs；综合考虑炸药爆炸能量利用率和成缝效果，最佳的后爆孔孔距为70cm。科学地采用时序控制预裂爆破不仅可以减小钻孔工作量与炸药用量，还能降低对岩体的损伤，可为地下厂房爆破开挖安全、高效的进行提供一条有效的途径。
- 时序控制预裂爆破 /
- 起爆延期时间 /
- 后爆孔孔距 /
- 现场试验
Abstract: In view of the underground powerhouse excavation work by blasting at the Baihetan Hydropower Station Project, in order to reduce the blasting-involved damage to the rock mass, numerical simulation and field test were carried out to analyze the influence of the initiation delay time and the distance between later detonated holes on the blasting and the cracking with time sequence controlled pre-splitting blasting, and the reasonable delay time and the optimum distance between post-detonated holes were obtained. The results show that when the hole diameter is 42 mm and the distance between the pre-detonated holes is 35 cm, the reasonable initiation delay time is 75~100 μs, and the optimum distance between the post-detonated holes is 70cm, with joint consideration of the blasting energy's utilization ratio and blasting effect. It is found that time sequence controlled pre-splitting blasting, used scientifically, is a safe and efficient method to excavate the rock mass close to the underground powerhouse wall, which can reduce the load of blasting, cut down on the explosives used, and limit the blasting-involved damage to rock mass.
- time sequence controlled pre-splitting blasting /
- initiation delay time /
- distance between later detonated holes /
- field test

HTML全文

图 1 时序控制预裂爆破示意图

Figure 1. Schematic diagram of time controlled pre-splitting blasting

下载: 全尺寸图片幻灯片

图 2 几何模型(单位：cm)

Figure 2. Geometric model(unit:cm)

下载: 全尺寸图片幻灯片

图 3 有限元网格模型

Figure 3. Finite element model

下载: 全尺寸图片幻灯片

图 4 不同起爆延期时间工况最大拉应力值

Figure 4. Maximum tensile stress with different initiation delay times

下载: 全尺寸图片幻灯片

图 5 199.75μs时不同后爆孔孔距的应力云图

Figure 5. Stress contour with different distances between later detonated holes at 199.75μs

下载: 全尺寸图片幻灯片

图 6 不同后爆孔孔距各监测点最大拉应力变化曲线

Figure 6. Maximum tensile stress value of the monitored points wih different distances between later detonated holes

下载: 全尺寸图片幻灯片

图 7 不同后爆孔孔距各监测点速度峰值变化曲线

Figure 7. Peak velocity of the monitored points with different distances between later detonated holes

下载: 全尺寸图片幻灯片

图 8 试验装药结构图

Figure 8. Charge structure

下载: 全尺寸图片幻灯片

图 9 试验起爆网路图

Figure 9. Detonating network

下载: 全尺寸图片幻灯片

图 10 后爆孔为70cm的爆破效果图

Figure 10. Blasting effect (observed when the distance between the later detonated holes is 70 cm)

下载: 全尺寸图片幻灯片

表 1 岩石参数

Table 1. Rock parameters

材料	密度/(kg·m^-3)	弹性模量/GPa	泊松比	屈服强度/MPa	切线模量/GPa
玄武岩	2870	35	0.22	120	13.5

下载: 导出CSV

表 2 岩石参数

Table 2. Rock parameters

A/GPa	B/GPa	R₁	R₂	ω	E₀/GPa	V₀
214.4	0.182	4.2	1.0	0.15	4.19	1.0

下载: 导出CSV

参考文献(16)

[1]	罗勇, 沈兆武.聚能药包在岩石定向断裂爆破中的应用研究[J].爆炸与冲击, 2006, 26(3):250-255. http://www.bzycj.cn/CN/abstract/abstract9229.shtml Luo Yong, Shen Zhaowu.Application study on directional fracture controlled blasting with shaped charge in rock[J].Explosion and Shock Waves, 2015, 26(3):250-255. http://www.bzycj.cn/CN/abstract/abstract9229.shtml
[2]	徐颖, 沈兆武, 孟益平.爆炸载荷作用下刻槽炮孔动态裂纹扩展规律[J].中国科学技术大学学报, 2003, 33(2):184-189. doi: 10.3969/j.issn.0253-2778.2003.02.009 Xu Ying, Shen Zhaowu, Meng Yiping.Investigation on dynamic expanding rule and application in notch blasting[J].Journal of University of Science and Technology of China, 2003, 33(2):184-189. doi: 10.3969/j.issn.0253-2778.2003.02.009
[3]	文梼, 谭海.岩石爆破中的空孔效应数值计算分析[J].爆破, 2011, 28(3):58-61. http://d.old.wanfangdata.com.cn/Periodical/bp201103017 Wen Tao, Tan Hai.The empty hole effect numerical computation analysis during rock blasting[J].Blasting, 2011, 28(3):59-61. http://d.old.wanfangdata.com.cn/Periodical/bp201103017
[4]	Zhu Ruigeng.Study for time-order-controlled fracture in the exaction of lager rock caverns[J].Symposium Large Rock Caverns in Finland, 1986.
[5]	Zhu Ruigeng, Cheng Kang, Lu Wenxing.A new method of fracture blast by time-order-ignition[J].Journal of Wuhan University of Technology, 1993, 1(1):40-46. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=WLGY199301004&dbname=CJFD&dbcode=CJFQ
[6]	程康.时序控制断裂爆破方法工业性试验研究[J].爆破器材, 1993, 75(4):27-29. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001128030 Cheng Kang.The experimental study on industrial of time controlled fracture blasting[J].Explosive Materials, 1993, 75(4):27-29. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000001128030
[7]	沈兴付.时序控制断裂爆破的计算机模拟分析[J].爆破, 2000, 4(17):117-122. http://d.old.wanfangdata.com.cn/Periodical/bp200004032 Shen Xingfu.Computer simulation analysis of sequential controlled rupture blasting[J].Blasting, 2000, 4(17):117-122. http://d.old.wanfangdata.com.cn/Periodical/bp200004032
[8]	岳中文, 郭洋, 许鹏, 等.定向断裂控制爆破的空孔效应实验分析[J].爆炸与冲击, 2015, 35(3):304-311. http://www.bzycj.cn/CN/abstract/abstract9464.shtml Yue Zhongwen, Guo Yang, Xu Peng, et al.Analysis of empty hole effect in directional fracture controlled blasting[J].Explosion and Shock Waves, 2015, 35(3):304-311. http://www.bzycj.cn/CN/abstract/abstract9464.shtml
[9]	王汉军, 黄风雷, 张庆明.岩石定向断裂爆破的力学分析及参数研究[J].煤炭学报, 2003, 28(4):399-402. doi: 10.3321/j.issn:0253-9993.2003.04.014 Wang Hanjun, Huang Fenglei, Zhang Qingming.Mechanics effect analysis and parameters study on borehole directional fracture blasting[J].Journal of China Coal Society, 2003, 28(4):399-402. doi: 10.3321/j.issn:0253-9993.2003.04.014
[10]	朱瑞赓, 李新平, 陆文兴.控制爆破的断裂控制与参数确定[J].爆炸与冲击, 1994, 14(4):314-317. doi: 10.3321/j.issn:1001-1455.1994.04.001 Zhu Ruigeng, Li Xinping, Lu wenxing.The determination of fracture control and parameter in controlled blasting[J].Explosion and Shock Waves, 1994, 14(4):314-317. doi: 10.3321/j.issn:1001-1455.1994.04.001
[11]	郦正能.工程断裂力学[M].北京:北京航空航天大学出版社, 2012.
[12]	李洪涛.大型地下厂房施工程序及开挖方法研究[D].武汉: 武汉大学, 2004. http://cdmd.cnki.com.cn/article/cdmd-10486-2004112177.htm
[13]	夏祥.爆炸荷载作用下岩体损伤特征及安全阀值研究[D].武汉: 中国科学院研究生院, 2006. http://cdmd.cnki.com.cn/Article/CDMD-80005-2006175944.htm
[14]	黄其冲.切缝药包爆破数值分析与应用研究[D].武汉: 武汉理工大学, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10497-1015001684.htm
[15]	刘优平, 龚敏, 黄刚海.深孔爆破装药结构优选数值分析方法及其应用[J].岩土力学, 2012, 33(6):1883-1888. doi: 10.3969/j.issn.1000-7598.2012.06.043 Liu Youping, Gong Min, Huang Ganghai.Numerical analysis method for optimizing charging structure of deep-hole blasting and its application[J].Rock and Soil Mechanics, 2012, 33(6):1883-1888. doi: 10.3969/j.issn.1000-7598.2012.06.043
[16]	Langefors U, Kihlstrom B.The modern technique of rock blasting[M].New York, USA:John Wiley and Sons Inc, 1973.