圆形中空夹层钢管超高性能钢纤维混凝土柱抗爆性能野外实验与数值模拟

徐慎春; 刘中宪; 吴成清

doi:10.11883/1001-1455(2017)04-0649-12

圆形中空夹层钢管超高性能钢纤维混凝土柱抗爆性能野外实验与数值模拟

doi: 10.11883/1001-1455(2017)04-0649-12

徐慎春¹,
刘中宪^2, ,,
吴成清^{1, 2}

1.
天津大学建筑工程学院，天津 300372
2.
天津城建大学天津市土木建筑结构防护与加固重点实验室，天津 300384

基金项目:

国家自然科学基金面上项目 51278326

国家科技支撑计划重点项目 2012BAJ07B05

天津市科技支撑计划重点项目 14ZCZDSF00016

详细信息

作者简介:
徐慎春(1986-)，男，博士

通讯作者:
刘中宪，zhongxian1212@163.com

中图分类号: O381
计量
- 文章访问数: 4003
- HTML全文浏览量: 1280
- PDF下载量: 239
- 被引次数: 0
出版历程
- 收稿日期: 2015-12-28
- 修回日期: 2016-05-15
- 刊出日期: 2017-07-25

Field blast test and numerical simulation of ultra-high performance steel fiber reinforced concrete-filled double skin steel tube column under blast loading

1.
School of Civil Engineering, Tianjin University, Tianjin 300372, China
2.
Tianjin Key Laboratory of Civil Structure Protection and Reinforcement, Tianjin Chengjian University, Tianjin 300384, China

摘要

摘要: 通过6根圆形中空夹层钢管超高性能钢纤维混凝土(UHPSFRCFDST)柱爆炸破坏实验，研究了轴压、折合距离、空心率和迎爆面形状对其动态响应及损伤破坏的影响，并运用LS-DYNA软件建立了爆炸荷载作用下UHPSFRCFDST柱动态响应的有限元模型。在验证了模型有效性的基础上，运用参数化分析方法，研究了轴压比、空心率、含钢率、内层和外层钢管径厚比及其强度等关键参数对圆形UHPSFRCFDST柱抗爆性能的影响。结果表明：有限元模型能够有效地分析UHPSFRCFDST柱在爆炸荷载作用下的动态响应及损伤破坏；在小于临界轴压时，提高轴压比能够提升UHPSFRCFDST柱抗爆性能，但超过临界轴压后继续提高反而会加重其损伤破坏；减小空心率或内、外层钢管径厚比均可有效提升UHPSFRCFDST柱的抗爆性能，提高含钢率或外层钢管强度也能达到相同效果，但提高内层钢管强度对其抗爆性能的提升作用并不显著。
- 中空夹层钢管超高性能钢纤维混凝土 /
- 爆炸荷载 /
- 抗爆性能 /
- 有限元模型
Abstract: A field blast test including 6 specimens was conducted to investigate the effect of the axial compression ratio, the scaled distance, the hollow ratio and the shape of the facing blasting side on the dynamic response of ultra-high performance steel fiber reinforced concrete-filled double skin steel tube columns (UHPSFRCFDST). Then a three dimensional finite element model (3D FEM) was built using the LS-DYNA software to analyse the dynamic response and damage mechanism of UHPSFRCFDST columns under blast loading, and it was validated by comparison of simulation with blast testing results. Based on this model, the effect of such key parameters as the axial compression ratio, the hollow ratio, the steel ration, the thickness and strength of the inner or outer steel tube, on the blast-resisting performance of UHPSFRCFDST columns was presented. The results indicate that the 3D FEM can accurately describe the dynamic response of UHPSFRCFDST columns under blast loading. The blast-resisting performance of UHPSFRCFDST columns can be improved by increasing the axial compression ratio in a certain range, whereas the damage of the specimens will aggravate when this ratio goes above a critical value. Moreover, the blast-resisting performance of UHPSFRCFDST columns can be enhanced by reducing the hollow ratio or the diameter to thickness ratio of the inner and outer steel tube, and the effect can also be achieved by increasing the steel proportion or the strength of the outer steel tube. However, the strength of the inner steel tube has little effect on the blast-resisting performance of UHPSFRCFDST columns.
- UHPSFRCFDST /
- blast loading /
- blast-resisting performance /
- finite element model

HTML全文

图 1 圆形UPHSFRCFDST柱截面示意图

Figure 1. Diagram of UPHSFRCFDST cross section

下载: 全尺寸图片幻灯片

图 2 爆炸破坏实验设置

Figure 2. Field blast test setup

下载: 全尺寸图片幻灯片

图 3 爆炸破坏实验示意图

Figure 3. Schematic of field blast test

下载: 全尺寸图片幻灯片

图 4 不同折合距离下超压时程曲线

Figure 4. Time history of overpressure with different scaled distances

下载: 全尺寸图片幻灯片

图 5 不同工况条件下柱跨中挠度时程曲线

Figure 5. Time history of mid-span displacement with different working conditions

下载: 全尺寸图片幻灯片

图 6 实验后试件

Figure 6. Specimens after test

下载: 全尺寸图片幻灯片

图 7 有限元模型

Figure 7. Finite element model

下载: 全尺寸图片幻灯片

图 8 试件柱中竖向位移时程曲线对比

Figure 8. Comparison of mid-span displacement history

下载: 全尺寸图片幻灯片

图 9 试件破坏形态对比

Figure 9. Comparison of failure modes

下载: 全尺寸图片幻灯片

图 10 不同轴压比时试件的柱中竖向位移时程曲线

Figure 10. Comparison of mid-span displacement history with different axial load ratios

下载: 全尺寸图片幻灯片

图 11 不同轴压比试件第一主应力云图

Figure 11. Contours of the first principal stress with different axial load ratios

下载: 全尺寸图片幻灯片

图 12 不同轴压比时柱中峰值位移

Figure 12. Peak mid-span displacements with different axial load ratios

下载: 全尺寸图片幻灯片

图 13 不同空心率时试件的柱中位移时程曲线

Figure 13. Time history of mid-span displacement with different hollow ratios

下载: 全尺寸图片幻灯片

图 14 不同空心率时试件的第一主应力云图

Figure 14. Contours of the first principal stress with different hollow ratios

下载: 全尺寸图片幻灯片

图 15 不同含钢率试件柱中位移时程曲线

Figure 15. Time history of mid-span displacement with different steel ratios

下载: 全尺寸图片幻灯片

图 16 不同含钢率试件的第一主应力云图

Figure 16. Contours of the first principal stress with different steel ratios

下载: 全尺寸图片幻灯片

图 17 内层钢管径厚比不同的试件柱中位移时程曲线

Figure 17. Time history of mid-span displacement with different diameter-thickness ratios of inner tube

下载: 全尺寸图片幻灯片

图 18 不同含钢率试件的第一主应力云图

Figure 18. Contours of the first principal stress with different diameter-thickness ratios of inner tube

下载: 全尺寸图片幻灯片

图 19 外层钢管径厚比不同试件的柱中位移时程曲线

Figure 19. Time history of mid-span displacement with different-diameter thickness ratios of outer tube

下载: 全尺寸图片幻灯片

图 20 外层钢管径厚比不同试件的第一主应力云图

Figure 20. Contours of the first principal stress with different diameter-thickness ratios of outer tube

下载: 全尺寸图片幻灯片

图 21 内层钢管强度不同试件的柱中位移时程曲线

Figure 21. Time history of mid-span displacement with different strengths of inner tube

下载: 全尺寸图片幻灯片

图 22 内层钢管强度不同试件的第一主应力云图

Figure 22. Contours of the first principal stress with different strengths of inner tube

下载: 全尺寸图片幻灯片

图 23 外层钢管强度不同试件的柱中位移时程曲线

Figure 23. Time history of mid-span displacement with different strengths of outer tube

下载: 全尺寸图片幻灯片

图 24 外层钢管强度不同试件的第一主应力云图

Figure 24. Contours of the first principal stress with different strengths of inner tube

下载: 全尺寸图片幻灯片

表 1 位移传感器参数

Table 1. Parameters of LVDTs

行程/mm	机械行程/mm	线性精度/%	电阻/kΩ	解析度	重复性精度/mm	使用温度/℃
125	132	0.08	5	Infinite无断解析	0.01	-60~150

下载: 导出CSV

表 2 压力传感器参数

Table 2. Parameters of pressure sensors

灵敏度/(mV·kPa^-1)	分辨率/kPa	量程/MPa	最大过载/MPa	谐振频率/kHz	温度范围/℃	瞬时温度/℃
0.15 ±0.007	0.69	69	103.4	≥500	-73~135	1 650

下载: 导出CSV

表 3 试件实验参数

Table 3. Experiment parameters of specimen

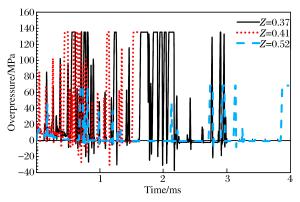
编号	轴压/kN	Z/(m·kg^-1/3)	空心率	放置方式
C4A	0	0.41	0.25	顶面齐平
C5A	1 000	0.41	0.25	顶面齐平
C4B	0	0.41	0.25	中面齐平
C5B	0	0.52	0.25	中面齐平
C6A	1 000	0.37	0.25	中面齐平
C6B	1 000	0.37	0	中面齐平

下载: 导出CSV

表 4 不同折合距离下的反射超压

Table 4. Overpressure with different scaled distances

Z/(m·kg^-1/3)	p_r/MPa
0.37	85.4
0.41	82.4
0.52	44.1

下载: 导出CSV

表 5 UHPSFRC本构关键参数

Table 5. Key parameters of UHPSFRC material model

b₁	b₂	b₃	LocWidth	OMEGA
1.75	1.35	1.15	0.025 4	0.5

下载: 导出CSV

表 6 关键参数对比

Table 6. Comparison of key parameters

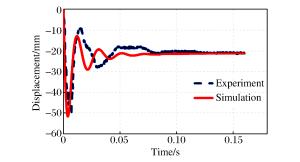
D_f/mm		误差/%
实验	模拟	误差/%
50.5	51.6	2.2

D_p/mm		误差/%
实验	模拟	误差/%
20.9	21.1	1.0

下载: 导出CSV

表 7 关键参数对比

Table 7. Comparison of key parameters

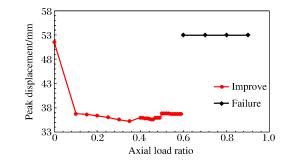
u	D_f	D_p
0	51.6	21.1
0.4	36.0 (-30.2%)	17.4 (-17.5%)
0.6	-	-
注：小括号内数字表示相对于u=0时所得结果的误差，“-”表示试件丧失承载能力。

下载: 导出CSV

表 8 关键参数对比

Table 8. Comparison of key parameters

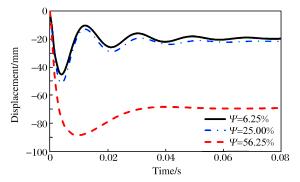
Ψ/%	D_f/mm	D_p/mm
6.25	45.0 (-12.8%)	19.6 (-7.7%)
25.00	51.6	21.1
56.25	88.6 (71.7%)	69.3 (228%)
注：小括号内数字表示相对于Ψ=25.00%时所得结果的误差。

下载: 导出CSV

表 9 关键参数对比

Table 9. Comparison of key parameters

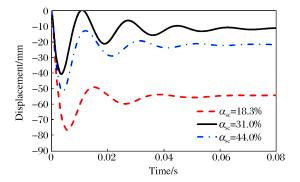
α_sc/%	D_f/mm	D_p/mm
18.3	76.6 (48.4%)	54.4 (157.8%)
31.0	51.6	21.1
44.0	40.6 (-21.3%)	11.2 (-46.9%)
注：小括号内数字表示相对于α_sc=31.0%时所得结果的误差。

下载: 导出CSV

表 10 关键参数对比

Table 10. Comparison of key parameters

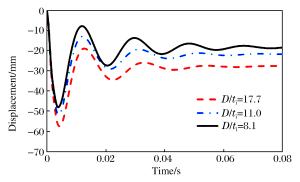
D/t_i	D_f/mm	D_p/mm
17.7	57.3 (11.0%)	27.5 (30.3%)
11.0	51.6	21.1
8.1	47.9 (-7.2%)	18.4 (-12.8%)
注：小括号内数字表示相对于D/t_i=11.0时所得结果的误差。

下载: 导出CSV

表 11 关键参数对比

Table 11. Comparison of key parameters

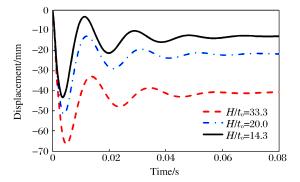
H/t_o	D_f/mm	D_p/mm
33.3	66.6 (29.1%)	40.7 (93.0%)
20.0	51.6	21.1
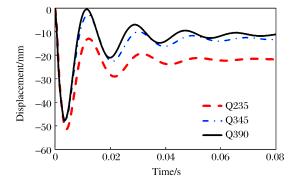
14.3	43.1 (-16.5%)	12.8 (-39.3%)
注：小括号内数字表示相对于H/t_o=20.0时所得结果的误差。

下载: 导出CSV

表 12 关键参数对比

Table 12. Comparison of key parameters

钢材	D_f/mm	D_p/mm
Q235	51.6	21.1
Q345	50.7 (-1.7%)	19.1 (-9.5%)
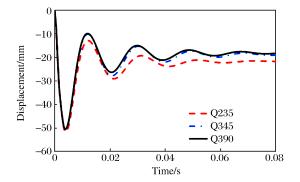
Q390	50.5 (-2.1%)	18.3 (-13.3%)
注：小括号内数字表示相对于内层钢管钢材为Q235时所得结果的误差。

下载: 导出CSV

表 13 关键参数对比

Table 13. Comparison of key parameters

钢材	D_f/mm	D_p/mm
Q235	51.6	21.1
Q345	48.4 (-6.2%)	13.3 (-37.0%)
Q390	47.7 (-7.6%)	18.3 (-47.4%)
注：小括号内数字表示相对于外层钢管钢材为Q235时所得结果的误差。

下载: 导出CSV

参考文献(20)

[1]	钟善桐.钢管混凝土结构[M].3版.北京:清华大学出版社, 2003.
[2]	蔡绍怀.现代钢管混凝土结构[M].北京:人民交通出版社, 2007.
[3]	韩林海.钢管混凝土结构——理论与实践[M].北京:科学出版社, 2004.
[4]	黄宏.中空夹层钢管混凝土压弯构件的力学性能研究[D].福州: 福州大学, 2006.
[5]	孙珊珊.爆炸荷载下钢管混凝土柱抗爆性能研究[D].西安: 长安大学, 2013.
[6]	崔莹.爆炸荷载下复式空心钢管混凝土柱的动态响应及损伤评估[D].西安: 长安大学, 2013.
[7]	李国强, 瞿海雁, 杨涛春, 等.钢管混凝土柱抗爆性能试验研究[J].建筑结构学报, 2013, 34(12):69-76. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201312009 Li Guoqiang, Qu Haiyan, Yang Taochun, et al. Experimental study of concrete-filled steel tubular columns under blast loading[J]. Journal of Building Structures, 2013, 34(12):69-76. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb201312009
[8]	Zhang F R, Wu C Q, Wang H W, et al. Numerical simulation of concrete filled steel tube columns against blast loads[J]. Thin-Walled Structures, 2015, 92:82-92. doi: 10.1016/j.tws.2015.02.020
[9]	Jama H H, Bambach M R, Nurick G N, et al. Numerical modelling of square tubular steel beams subjected to transverse blast loads[J]. Thin-Walled Structures, 2009, 47(12):1523-1534. doi: 10.1016/j.tws.2009.06.004
[10]	余同希, 邱信明.冲击动力学[M].北京:清华大学出版社, 2011.
[11]	Livermore Software Technology Corporation. LS-DYNA User's Manual, Version971[M]. Livermore, CA: Livermore Software Technology Corporation, 2015.
[12]	李忠献, 师燕超, 史祥生.爆炸荷载作用下钢筋混凝土板破坏评定方法[J].建筑结构学报, 2009, 30(6):60-66. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb200906008 Li Zhongxian, Shi Yanchao, Shi Xiangsheng. Damage analysis and assessment of RC slabs under blast load[J]. Journal of Building Structures, 2009, 30(6):60-66. http://d.old.wanfangdata.com.cn/Periodical/jzjgxb200906008
[13]	师燕超, 李忠献.爆炸荷载作用下钢筋混凝土柱的动力响应与破坏模式[J].建筑结构学报, 2008, 29(4):112-117. doi: 10.3321/j.issn:1000-6869.2008.04.015 Shi Yanchao, Li Zhongxian. Dynamic responses and failure modes of RC columns under blast loading[J]. Journal of Building Structures, 2008, 29(4):112-117. doi: 10.3321/j.issn:1000-6869.2008.04.015
[14]	Bauschinger J. On the change of position of the elastic limit of iron and steel under cyclic variations of stress[J]. Mitt Mech Tech Lab München, 1886(13):101-115.
[15]	Malvar L J, Crawford J E, Wesevich J W, et al. A plasticity concrete material model for DYNA3D[J]. International Journal of Impact Engineering, 1997, 19(9/10):847-873. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=CC025950745
[16]	Tu Z, Lu Y. Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J]. International Journal of Impact Engineering, 2009, 36(1):132-146. doi: 10.1016/j.ijimpeng.2007.12.010
[17]	Malvar L J, Crawfor J E, Morrill K B. K&C concrete material model release Ⅲ: Automated generation of material model input: TR-99-24-B1[R]. Glendale: Karagozian and Case Structural Engineers, 2009.
[18]	Gopalaratnam V S, Shah S P. Properties of steel fiber reinforced concrete subjected to impact loading[J]. Journal of the American Concrete Institute, 1986, 83(1):117-126. https://www.concrete.org/publications/internationalconcreteabstractsportal/m/details/id/1750
[19]	Wang Z L, Liu Y S, Shen R F. Stress-strain relationship of steel fiber-reinforced concrete under dynamic compression[J]. Construction and Building Materials, 2008, 22(5):811-819. doi: 10.1016/j.conbuildmat.2007.01.005
[20]	赵均海, 郭红香, 魏雪英.圆中空夹层钢管混凝土柱承载力研究[J].建筑科学与工程学报, 2005, 22(1):50-54. doi: 10.3321/j.issn:1673-2049.2005.01.007 Zhao Junhai, Guo Hongxiang, Wei Xueying. Research on bearing capacity of concrete filled double skin steel tubes column[J]. Journal of Architecture and Civil Engineering, 2005, 22(1):50-54. doi: 10.3321/j.issn:1673-2049.2005.01.007