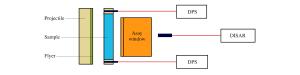
Asay window for probing the microspall of materials
-
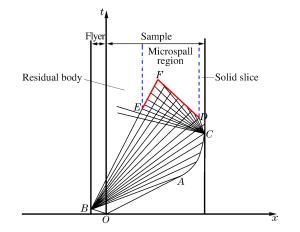
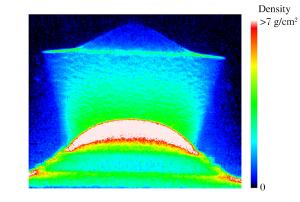
摘要: 微层裂是冲击波物理领域的重要基础问题，在工程上具有重要应用价值。近年来用于诊断样品多层层裂的传统Asay窗技术被用于诊断微层裂，但对其诊断能力和信号特征认识仍存在严重不足。为此，通过波系分析，揭示出在薄飞片击靶的微层裂实验中样品破碎存在1个“痂片”特征区、2个微层裂特征区以及1个“残体”特征区。实验表明，在样品窗口间隙合适的条件下，Asay窗不仅能够有效区分这些不同特征分区，而且能够灵敏探测样品表面发射的高速微喷粒子，从而实现对样品连续破碎过程的精密诊断。Abstract: Microspall is an essential problem in both theoretical investigation and engineering application in shock physics. The Asay window, originally developed to diagnose the multi-spall behavior of material, was recently employed to probe the microspall, but its ability for probing the problem calls for further demonstration, and the corresponding signal also needs further explanation. In this paper, wave propagation analysis indicates that the sample bearing microspall can be separated into several different characteristic regions, the experiments performed demonstrate that the Asay window can sensitively distinguish these regions as far as a reasonable experimental configuration is set up, and even the features of the micro jet particles can be detected. So the technique was proved of great value for dynamic fragmentation studies.
-
Key words:
- Asay window /
- wave propagation analysis /
- microspall /
- shock wave
-
图 1 较早报道的Asay窗诊断样品微层裂时所测的速度剖面
Figure 1. Earlier reported velocity profiles measured by Asay window in microspall experiments
图 3 实测的Asay窗粒子速度剖面
Figure 3. Measured velocity profiles by Asay window for all experiments
表 1 实验参数及结果
Table 1. Experimental parameters and results
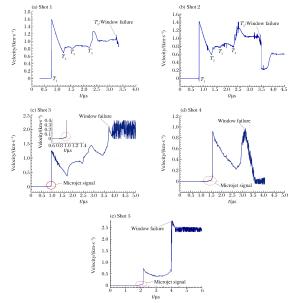
实验编号 df/mm ds/mm d/mm v/(km·s-1) Shot 1 0.508 2.522 0.3 3.244 Shot 2 0.505 2.524 0.5 3.200 Shot 3 0.503 2.522 1.0 3.254 Shot 4 0.507 2.525 3.0 3.255 Shot 5 0.500 2.521 5.0 3.252 
下载: 导出CSV
-
[1] Curran D R, Seaman L, Shockey D A. Dynamic failure of solids[J]. Physics Reports, 1987, 147(5):253-388. doi: 10.4028-www.scientific.net-KEM.261-263.239/ [2] 白以龙, 柯孚久, 夏蒙棼.固体中微裂纹系统统计演化的基本描述[J].力学学报, 1991, 23(3):290-298. http://www.cnki.com.cn/Article/CJFDTOTAL-LXXB199103004.htmBai Yilong, Ke Fujiu, Xia Mengfen. Formulation of statistical evolution of microcracks in solids[J]. Acta Mechanica Sinica, 1991, 23(3):290-298. http://www.cnki.com.cn/Article/CJFDTOTAL-LXXB199103004.htm [3] 黄筑平, 杨黎明, 潘客麟.材料的动态损伤和失效[J].力学进展, 1993, 23(4):433-467. http://d.old.wanfangdata.com.cn/Periodical/gthjjs201304023Huang Zhuping, Yang Liming, Pan Kelin. Dynamic damage and failure of materials[J]. Advances in Mechanics, 1993, 23(4):433-467. http://d.old.wanfangdata.com.cn/Periodical/gthjjs201304023 [4] Zhang L, Cai L C, Li Y L, et al. Simplified model for prediction of dynamic damage and fracture of ductile materials[J]. International Journal of Solids & Structures, 2004, 41(24):7063-7074. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=e7d9d8472fd17f65ef142c3ced83b26c [5] 张林.延性材料冲击响应: 动态损伤与断裂、结构相变的新模型[D].绵阳: 中国工程物理研究院, 2005. http://cdmd.cnki.com.cn/Article/CDMD-82818-2005136415.htm [6] 陈永涛, 唐小军, 李庆忠, 等.纯铁材料的冲击相变与"反常"层裂[J].爆炸与冲击, 2009, 29(6):638-641. doi: 10.11883/1001-1455(2009)06-0637-05Chen Yongtao, Tang Xiaojun, Li Qingzhong, et al. Phase transition and abnormal spallation in pure iron[J]. Explosion and Shock Waves, 2009, 29(6):638-641. doi: 10.11883/1001-1455(2009)06-0637-05 [7] 陈永涛, 唐小军, 李庆忠.Fe基α相合金的冲击相变及其对层裂行为的影响研究[J].物理学报, 2011, 60(4):486-494. http://d.old.wanfangdata.com.cn/Periodical/wlxb201104079Chen Yongtao, Tang Xiaojun, Li Qingzhong. Phase transition and influence of phase transition on spall in α phase Fe-based alloy[J]. Acta Physica Sinica, 2011, 60(4):486-494. http://d.old.wanfangdata.com.cn/Periodical/wlxb201104079 [8] 章杰, 苏少卿, 郑宇, 等.改进SPH方法在陶瓷材料层裂数值模拟中的应用[J].爆炸与冲击, 2013, 33(4):401-407. doi: 10.3969/j.issn.1001-1455.2013.04.011Zhang Jie, Su Shaoqing, Zheng Yu, et al. Application of modified SPH method to numerical simulation of ceramic spallation[J]. Explosion and Shock Waves, 2013, 33(4):401-407. doi: 10.3969/j.issn.1001-1455.2013.04.011 [9] 彭辉, 李平, 裴晓阳, 等.动态损伤演化的空间不连续性实验研究[J].物理学报, 2013, 62(22):226201. doi: 10.7498/aps.62.226201Peng Hui, Li Ping, Pei Xiaoyang, et al. Experimental study of the spatial discontinuity of dynamic damage evolution[J]. Acta Physica Sinica, 2013, 62(22):226201. doi: 10.7498/aps.62.226201 [10] 贺红亮.动态拉伸断裂的物理判据研究[J].高压物理学报, 2013, 27(2):153-161. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gywlxb201302001He Hongliang. Physical criterion of dynamic tensile fracture[J]. Chinese Journal of High Pressure Physics, 2013, 27(2):153-161. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=gywlxb201302001 [11] 张林, 张祖根, 秦晓云, 等.D6A、921和45钢的动态破坏与低压冲击特性[J].高压物理学报, 2003, 17(4):305-310. doi: 10.3969/j.issn.1000-5773.2003.04.011Zhang Lin, Zhang Zugen, Qin Xiaoyun, et al. Dynamic fracture and mechanical property of D6A, 921 and 45 steels under low shock pressure[J]. Chinese Journal of High Pressure Physics, 2003, 17(4):305-310. doi: 10.3969/j.issn.1000-5773.2003.04.011 [12] 翟少栋, 李英华, 彭建祥, 等.平面碰撞与强激光加载下金属铝的层裂行为[J].爆炸与冲击, 2016, 36(6):767-773. doi: 10.11883/1001-1455(2016)06-0767-07Zhai Shaodong, Li Yinghua, Peng Jianxiang, et al. Spall behavior of pure aluminum under plate-impact and high energy laser shock loadings[J].Explosion and Shock Waves, 2016, 36(6):767-773. doi: 10.11883/1001-1455(2016)06-0767-07 [13] Barker L M, Hollenbach R E. Interferometer technique for measuring the dynamic mechanical properties of materials[J]. Review of Scientific Instruments, 1965, 36(11):1617-1620. doi: 10.1063/1.1719405 [14] 张林, 李英华, 陈大年, 等.金属材料层裂强度测量方法: GJB7368─2011[S].绵阳: 中国工程物理研究院, 2011. [15] 张万甲, 杨中正.93钨合金断裂特性研究[J].高压物理学报, 1995, 9(4):279-288. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199500150295Zhang Wanjia, Yang Zhongzheng. Studies on the fracture behaviour for 93 tungsten alloy[J]. Chinese Journal of High Pressure Physics, 1995, 9(4):279-288. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK199500150295 [16] Signor L, De Rességuier T, Dragon A, et al. Investigation of fragments size resulting from dynamic fragmentation in melted state of laser shock-loaded tin[J]. International Journal of Impact Engineering, 2010, 37(8):887-900. doi: 10.1016/j.ijimpeng.2010.03.001 [17] De Rességuier T, Loison D, Lescoute E, et al. Dynamic fragmentation of laser shock-melted metals: Some experimental advances[J]. Journal of Theoretical & Applied Mechanics, 2010, 48(4):957-972. [18] Luo S N, An Q, Germann T C, et al. Shock-induced spall in solid and liquid Cu at extreme strain rates[J]. Journal of Applied Physics, 2009, 106(1):013502. doi: 10.1063/1.3158062 [19] Holtkamp D B, Clark D A, Ferm E N, et al. A survey of high explosive-induced damage and spall in selected metals using proton radiography[C]//Furnish M D, Gupta Y M, Forbes J M. Shock Compression of Confensed Matter-2003. New York: American Institute of Physics, 2004: 477-482. [20] Lescoute E, De Rességuier T, Chevalier J M, et al. Transverse shadowgraphy and new recovery techniques to investigate dynamic fragmentation of laser shock-loaded metals[C]//Elert M L, Buttler W T, Furnish M D, et al.Shock Compression of Confensed Matter-2009. New York: American Institute of Physics, 2009: 1043-1046. [21] McCluskey C W, Wilke M D, Anderson W W, et al. Asay window: A new spall diagnostic[J]. Review of Scientific Instruments, 2006, 77(11):477-482. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ022448623/ [22] Signor L, Roy G, Chanal P Y, et al. Debris cloud ejection from shock-loaded tin melted on release or on compression[C]// Elert M L, Buttler W T, Furnish M D, et al. Shock Compression of Confensed Matter-2009. New York: American Institute of Physics, 2009: 1065-1068. [23] 陈永涛, 任国武, 汤铁钢, 等.爆轰加载下金属样品的熔化破碎现象诊断[J].物理学报, 2013, 62(11):116202. doi: 10.7498/aps.62.116202Chen Yongtao, Ren Guowu, Tang Tiegang, et al. Experimental diagnostic of melting fragments under explosive loading[J]. Acta Physica Sinica, 2013, 62(11):116202. doi: 10.7498/aps.62.116202 [24] 张林, 李雪梅, 李英华.锡的微层裂破碎复合Asay窗实验研究[C]//第五届全国强动载效应及防护学术会议暨复杂介质/结构的动态力学行为创新研究群体学术研讨会论文集.北京: 北京理工大学, 2013: 58-63. [25] Zhang L, Li Y H, Yu Y Y, et al. General construction of mean-field potential and its application to the multiphase equations of state of tin[J]. Physica B, 2011, 406(22):4163-4169. doi: 10.1016/j.physb.2011.01.018 [26] Marsh S P. LASL shock Hugoniot data[M]. Berkeley:University of California Press, 1980. [27] De Rességuier T, Signor L, Dragon A, et al. On the dynamic fragmentation of laser shock-melted tin[J]. Applied Physics Letters, 2008, 92(13):013506. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=9666c07b6bdf4a3874acb4f34361ac0d -
图(5) / 表(1)
计量
- 文章访问数: 4213
- HTML全文浏览量: 1309
- PDF下载量: 337
- 被引次数: 0