Conditions for shock wave induced flame instability and detonation
-
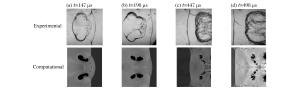
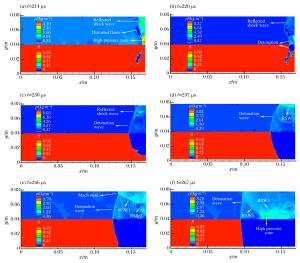
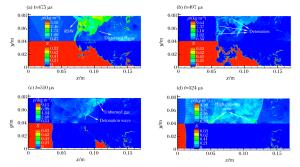
摘要: 采用九阶WENO和十阶中心差分格式数值求解激波与火焰作用过程，考察了激波强度、火焰尺寸对激波与球形火焰作用过程的影响。结果表明，增大激波强度或火焰尺寸均可在流场中引发爆轰，但激波强度的影响更大，并且其引发的爆轰可使火焰迅速膨胀，放热率提高，从而影响燃烧特性；此外，爆轰波传播过程中会迅速消耗可燃预混气，合并原有的反射激波，并在流场中形成局部高压区，极大地改变流场结构。Abstract: A computational study of the interaction between shock waves and a spherical flame was carried out using the ninth-order WENO and the tenth-order central difference schemes, and the influence of shock intensity and flame size on the interaction process was investigated. It can be found from the results of our study that the increase of the shock intensity and the flame size can both induce detonation in the flow field, but the influence of the shock intensity is relatively stronger. Further, the detonation induced by shock wave can lead to quick flame expansion and increase its heat release rate, thereby affecting the combustion characteristics. Besides, the detonation wave will quickly burn out the combustible gas, merge the previously existing reflected shock waves in the propagation process, and form local high pressure zones, which can significantly alter the flow field structure.
-
Key words:
- shock wave /
- flame /
- detonation /
- flow field structure
-
图 4 计算密度与质量分数(Case 3)
Figure 4. Images of computational density and mass fraction (Case 3)
图 5 计算密度与质量分数(Case 5)
Figure 5. Images of computational density and mass fraction (Case 5)
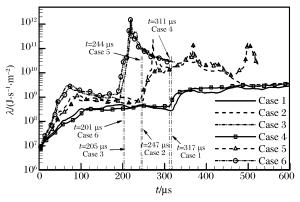
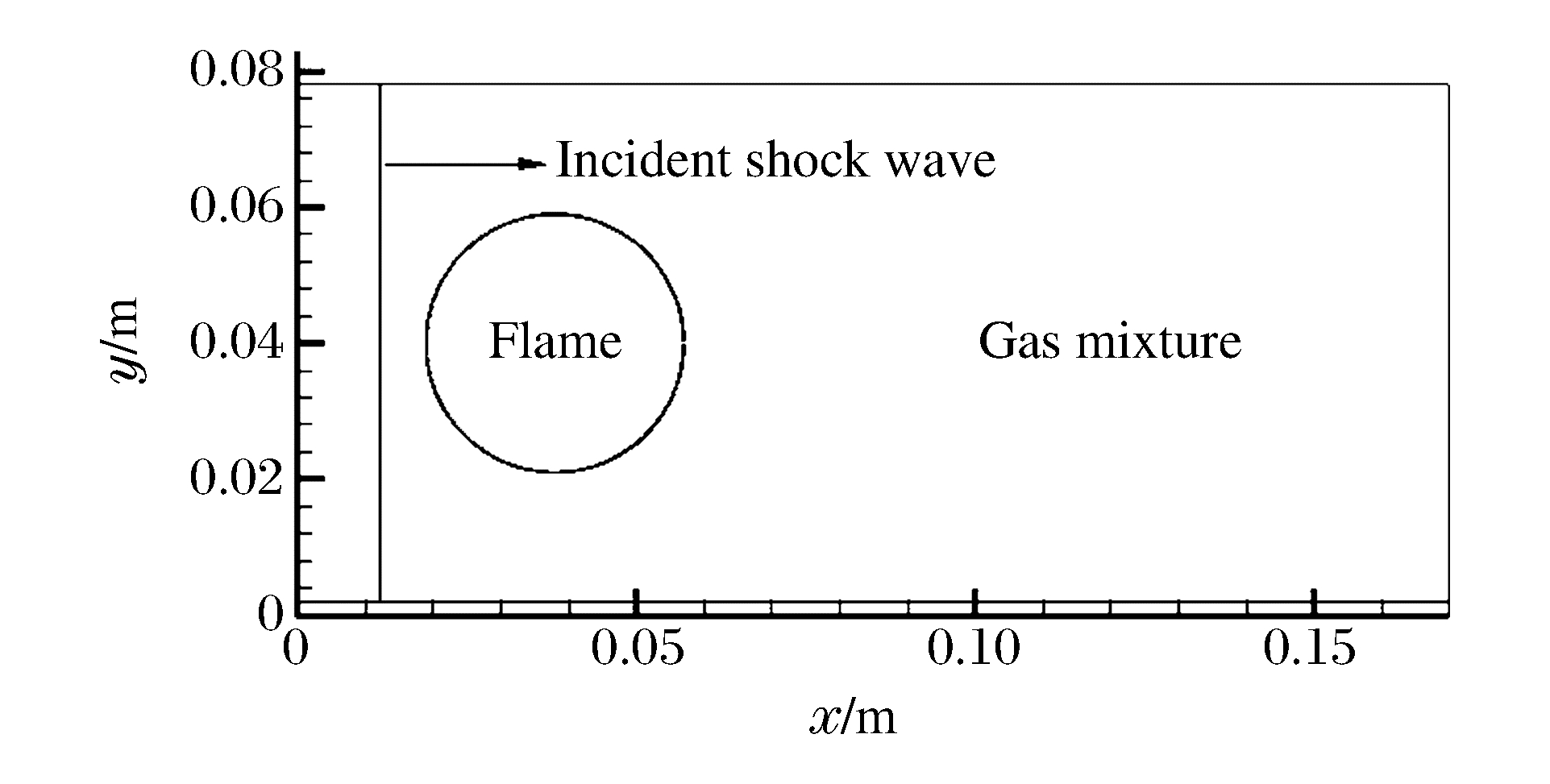
表 1 不同激波马赫数和火焰尺寸的4组算例
Table 1. Four cases with different shock Mach numbers and flame sizes
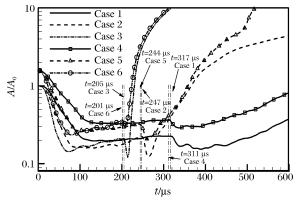
算例 Ma R0/m Case 1 1.7 0.019 Case 2 2.1 0.019 Case 3 2.5 0.019 Case 4 1.7 0.024 Case 5 2.1 0.024 Case 6 2.5 0.024 
下载: 导出CSV
-
[1] Marble F E, Hendricks G J, Zukoski E E. Progress toward shock enhancement of supersonic combustion processes[C]//23rd Joint Propulsion Conference. San Diego, CA, 1987. [2] Oran E S, Gamezo V N. Origins of the deflagration-to-detonation transition in gas-phase combustion[J]. Combustion and Flame, 2007, 148(1/2):4-47. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=4cf0d5c02c507b4281e25a3cd95da815 [3] Markstein G H. A shock-tube study of flame front-pressure wave interaction[J]. Symposium (International) on Combustion, 1957, 6(1):387-398. doi: 10.1016/S0082-0784(57)80054-X [4] Thomas G O, Bambrey R, Brown C. Experimental observations of flame acceleration and transition to detonation following shock-flame interaction[J]. Combustion Theory and Modelling, 2001, 5(4):573-594. doi: 10.1088/1364-7830/5/4/304 [5] Ju Y, Shimano A, Inoue O. Vorticity generation and flame distortion induced by shock flame interaction[J]. Symposium (International) on Combustion, 1998, 27(1):735-741. doi: 10.1016/S0082-0784(98)80467-0 [6] Khokhlov A M, Oran E S, Thomas G O. Numerical simulation of deflagration-to-detonation transition: The role of shock-flame interactions in turbulent flames[J]. Combustion and Flame, 1999, 117(1/2):323-339. [7] Khokhlov A M, Oran E S. Numerical simulation of detonation initiation in a flame brush: The role of hot spots[J]. Combustion and Flame, 1999, 119(4):400-416. doi: 10.1016/S0010-2180(99)00058-9 [8] Gamezo V N, Oran E S, Khokhlov A M. Three-dimensional reactive shock bifurcations[J]. Proceedings of the Combustion Institute, 2005, 30(2):1841-1847. doi: 10.1016/j.proci.2004.08.259 [9] Teng H H, Jiang Z L, Hu Z M. Detonation initiation developing from the Richtmyer-Meshkov instability[J]. Acta Mechanica Sinica, 2007, 23(4):343-349. doi: 10.1007/s10409-007-0085-2 [10] 谷壮志, 王超, 施红辉, 等.激波诱导火焰变形的数值模拟[J].浙江理工大学学报, 2011, 28(4):529-533. doi: 10.3969/j.issn.1673-3851.2011.04.010Gu Zhuangzhi, Wang Chao, Shi Honghui, et al. The numerical simulation of the flame deformation induced by shock wave[J]. Journal of Zhejiang Sci-Tech University, 2011, 28(4):529-533. doi: 10.3969/j.issn.1673-3851.2011.04.010 [11] Dong G, Fan B, Ye J. Numerical investigation of ethylene flame bubble instability induced by shock waves[J]. Shock Waves, 2008, 17(6):409-419. doi: 10.1007/s00193-008-0124-3 [12] 朱跃进, 董刚, 范宝春.受限空间内激波与火焰作用的三维计算[J].推进技术, 2012, 33(3):405-411. http://d.old.wanfangdata.com.cn/Periodical/tjjs201203011Zhu Yuejin, Dong Gang, Fan Baochun. Three-dimensional computation of the interactions between shock waves and flame in a confined space[J]. Journal of Propulsion Technology, 2012, 33(3):405-411. http://d.old.wanfangdata.com.cn/Periodical/tjjs201203011 [13] 朱跃进, 董刚, 刘怡昕, 等.激波诱导火焰变形、混合和燃烧的数值研究[J].爆炸与冲击, 2013, 33(4):430-437. doi: 10.3969/j.issn.1001-1455.2013.04.016Zhu Yuejin, Dong Gang, Liu Yixin, et al. A numerical study on shock induced distortion, mixing and combustion of flame[J]. Explosion and Shock Waves, 2013, 33(4):430-437. doi: 10.3969/j.issn.1001-1455.2013.04.016 [14] Zhu Y J, Dong G, Liu Y X. Three-dimensional numerical simulations of spherical flame evolutions in shock and reshock accelerated flows[J]. Combustion Science and Technology, 2013, 185(10):1415-1440. doi: 10.1080/00102202.2013.798656 [15] 朱跃进, 董刚.激波冲击火焰的涡量特性研究[J].爆炸与冲击, 2015, 35(6):839-845. doi: 10.11883/1001-1455(2015)06-0839-07Zhu Yuejin, Dong Gang. A study of vorticity characteristics of shock-flame interaction[J]. Explosion and Shock Waves, 2015, 35(6):839-845. doi: 10.11883/1001-1455(2015)06-0839-07 [16] Jiang G S, Shu C W. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126:202-228. doi: 10.1006/jcph.1996.0130 [17] 王革, 关奔.激波作用下R22气泡射流现象研究[J].力学学报, 2013, 45(5):707-715. http://d.old.wanfangdata.com.cn/Thesis/Y2235904Wang Ge, Guan Ben. A study on jet phenomenon of R22 gas cylinder under the impact of shock wave[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5):707-715. http://d.old.wanfangdata.com.cn/Thesis/Y2235904 [18] Gordon S, Mcbride B J. Computer program for calculation of complex chemical equilibrium compositions and application Ⅰ: analysis[Z]. NASA Reference Publication 1311, 1994. -
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 4492
- HTML全文浏览量: 1222
- PDF下载量: 378
- 被引次数: 0