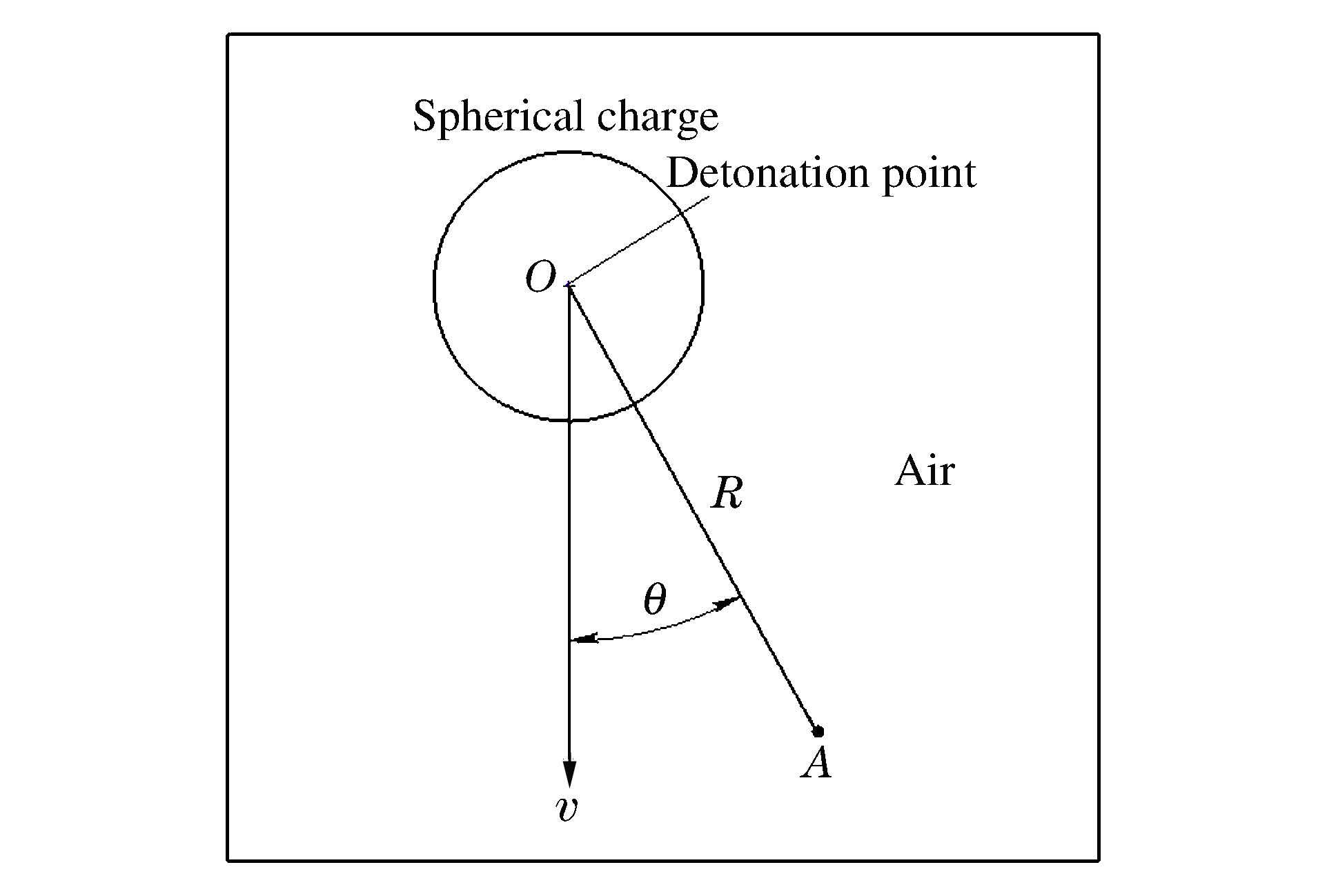
Overpressure calculation model of sphere charge blastingwith moving velocity
-
摘要: 为获得球形装药动态爆炸冲击波超压场计算模型，对静态爆炸冲击波超压Baker计算公式加入修正因子进行修正，并建立了构造包含装药运动速度、对比距离和方位角的修正因子函数的方法。为获得修正因子的函数表达式，采用高精度显式欧拉流体动力学软件SPEED针对具有典型运动速度的球形装药空中爆炸过程进行了数值模拟，得到了沿装药不同对比距离和方位角处的动态爆炸冲击波超压峰值。在对数值模拟结果处理的基础上，经过数据拟合获得了动态爆炸冲击波超压场计算模型。校验结果表明，该模型能较准确描述动态爆炸冲击波超压分布，具有普适性。Abstract: In order to establish a calculation model for the dynamic blast overpressure field, a correction factor was introduced into the Baker formula, a model for calculating the peak overpressure only in a static blast. The method to obtain the correction factor containing the moving velocity, the azimuth and the scaled distance was established. For getting the function of the correction factor, spherical charge models with the typical moving velocity were established using the shock physical explicit Eulerian dynamic (SPEED) to simulate the dynamic blast process in the air. The peak overpressure in the typical azimuth and scaled distance was obtained. Based on the numerical results, a new calculation model was constructed using the data fitted. The result of the numerical simulation indicates that the corrected formula is a universal calculation model, capable of predicting the peak overpressure in dynamic blast.
-
Key words:
- shockwave overpressure /
- dynamic blast /
- moving velocity /
- overpressure calculation model
-
反应装甲作为对抗聚能射流侵彻的有效装置之一，广泛应用于现代装甲车辆的防护，根据内层材料及其产生的效应不同，可分为爆炸反应装甲(explosive reactive armor, ERA)和被动反应装甲(passive armor)两大类[1-2]。其中爆炸反应装甲(也称平板装药)的典型结构为两层钢板夹层炸药组成的三明治结构，夹层炸药在射流的高速撞击下被引爆，驱动包覆板反向运动切割射流，使其产生断裂、偏折而失去侵彻能力。研究结果[3]显示：射流高速侵彻反应装甲过程中，在撞击点处形成一个高速扩张的孔，由于飞板运动和孔扩张的耦合，背板仅能与穿透反应装甲后射流头部后某处开始作用，未受到飞板干扰作用的射流部分称为逃逸射流。逃逸射流越长，后效穿深越大。因此，如何降低逃逸射流的长度是爆炸反应装甲设计的一个重要方向。研究人员试图采用新的结构设计来减少逃逸射流的长度，赵慧英等[4]通过反应装甲后附加装陶瓷复合装甲结构来提高其对逃逸射流的防护，H.J.Lee等[5]通过在反应装甲后加衬板减小逃逸射流的长度，采用AUTODYN软件模拟了衬板材料对其防护性能的影响，S.Friling等[6]通过在反应装甲后附加被动反应装甲以提高其防护能力，将射流简化为长杆对其作用过程进行了2D模拟，研究结果显示背板具有更高的速度，但是不能反映倾斜条件下与射流的作用过程。
被动反应装甲典型结构为两层钢板夹层惰性材料，由于具有射流防护效能好、附带损伤效应较小等优点而受到研究人员重视，目前已经有大量针对其防护性能及机理的研究[7-9]。本文中，通过将平板装药与橡胶复合板集成设计，采用实验和数值模拟方法研究其作为面板或背板时对射流的防护性能和机理，并与钢面板的反应装甲进行对比，以期为新型反应装甲的结构设计提供参考。
1. 实验研究
1.1 结构设计
为研究橡胶复合板位置对爆炸反应装甲防护性能的影响，设计了以橡胶复合板及钢面板作为面板或背板的3种反应装甲结构，如图 1所示。其中橡胶复合板由两层Q235钢板(厚度为1.2 mm)和硫化橡胶夹层(密度为1.01 g/cm3，厚度为1.5 mm)组成，其长度为150 mm，宽度为50 mm。将钢板表面清洗干净并进行喷砂处理，用调配好的环氧树脂溶液将钢板和橡胶粘结，室温下固化。橡胶复合板的等效钢厚为(0.12×2×7.85+1.5×1.01)/7.85 = 2.55 mm；而爆炸反应装甲包覆板材为Q235钢，厚度为2.5 mm，由此可知，3种结构爆炸反应装甲面密度基本相同。夹层炸药采用厚度为3 mm、装药密度为1.71 g/cm3的B炸药。此外，图 1中结构记号意义如下：“St”表示钢板，“Rubber”表示硫化橡胶层，“E”表示夹层炸药。
1.2 实验装置
采用装药口径36 mm聚四氟乙烯塑料壳体的聚能装药对反应装甲作引爆实验，其中铜药型罩壁厚为1 mm，锥角为60°，装药为JH-2。该聚能装药射流头部速度约为6.2 km/s，直径为1.5 mm，炸高为85 mm时对均质装甲钢的平均穿深为150 mm。
图 2为聚能装药对反应装甲作用的实验布置示意图。实验时聚能装药呈水平放置，口部距测试装甲表面、后效靶板分别为85、210 mm。反应装甲倾角30°，后效靶材为603均质装甲钢，厚度为50 mm，实验后通过测量残余穿深(depth of penetration, DOP)来比较3种装甲结构的防护性能，采用Scandish Flash-XT450脉冲X射线摄影系统对3种结构反应装甲与射流作用情况进行了观测。聚能装药采用电雷管起爆。
1.3 实验结果
图 3为脉冲X射线拍摄的射流与结构(b)和结构(c)作用时的典型时刻的X射线照片，图 4为逃逸射流对靶板表面的损伤情况。表 1为逃逸射流对靶板表面的损伤测量结果。从图 3可以看出，射流发生了偏转，由于稀疏波的影响，飞板边缘速度略低于其它部分；结构(b)的飞板速度约为860~880 m/s，背板与射流作用部位凸起现象不明显，而结构(c)背板与射流作用后呈花瓣形破裂，总体厚度明显大于钢飞板。在结构(c)背板前出现了逃逸射流颗粒，其长度约为6 mm，速度约为3 km/s。
表 1 实验结果Table 1. Experimental results of penetration装甲结构 开坑尺寸/(mm×mm) 开坑深度/mm 结构(a) 7×11 9 结构(b) 6×11 11 结构(c) 6×7 6 从图 4可以看出，射流与爆炸反应装甲作用后，在后效靶表面的损伤形成了多个开坑，由射流碎片高速撞击而成，大致可分为两个区域，一个是逃逸射流作用区(如图 4中箭头所示)，另外一个区域是背板飞离射流轴线后，射流后部碎片侵彻后效靶形成。橡胶复合板无论作为面板和背板，都可以减小逃逸射流的穿深，作为背板时效果更优，与钢反应装甲相比，穿深降低了46%。
从实验结果可以看出，橡胶复合板作为爆炸反应装甲面、背板时其防护性能优于钢反应装甲，特别是作为背板时后效穿深相比于钢反应装甲减小了5 mm。
2. 数值模拟
2.1 计算模型
利用非线性动态有限元ANSYS/LS-DYNA软件ALE算法对聚能装药与反应装甲的作用过程进行了数值模拟，其中空气和聚能装药采用欧拉算法，反应装甲采用拉格朗日算法。根据结构的对称性，建立了1/2计算模型，建模过程中施加对称约束和无反射边界条件。
2.2 材料模型参数
JH-2装药采用JWL状态方程和高能材料燃烧模型，夹层炸药Comp.B采用JWL状态方程和Lee-Tarver反应模型[10]描述，其表达式为：
p=A(1−ωR1V)e−R1V+B(1−ωR2V)e−R2V+ωE/V (1) dλdt=I(1−λ)b(ρρ0−1−a)x+G1(1−λ)cλdpy+G2(1−λ)eλgpz (2) 式中：V = ρ0/ρ，ρ为爆轰产物密度，ρ0为炸药初始装药密度；E = ρ0e，e为内能；A、B、R1、R2、ω为输入参数；λ为反应速率分数；t为时间，p为压力，I、b、a、x、G1、c、d、y、G2、e、g、z为常数。炸药的主要参数和Lee-Tarver反应模型参数分别如表 2和表 3所示。
表 2 炸药计算参数Table 2. Computational parameters for JH-2 and Comp.B炸药 ρ/(g·cm-3) D/(m·s-1) A/GPa B/GPa R1 R2 ω JH-2 1.685 8 130 625.3 23.29 5.25 1.6 0.28 Comp. B 1.715 7 980 524.2 7.77 4.2 1.1 0.50 表 3 Lee-Tarver反应模型参数Table 3. Computational parameters for Lee-Tarver modelI/s-1 b a x G1/GPa c d y G2/GPa e g z 4.4×1017 0.667 0 20 310 0.667 0.111 1.0 400 0.333 1.0 2.0 紫铜药型罩和包覆板材料Q235钢板的力学行为分别采用Johnson-Cook模型和Grüneison状态方程进行描述，材料的本构参数见表 4，其中A1、B1、C1、m、n为Johnson-Cook模型参数，c0为体积声速，Γ0为Grüneisen系数，s为常数。橡胶夹层和聚能壳体材料采用Grüneison状态方程和Hydro(Pmin)模型描述[1]，材料参数取值见表 5，其中σb为抗拉强度，ε为延伸率。
表 4 紫铜和Q235钢材料的本构方程计算参数Table 4. Computational parameters for copper and Q235 steel材料 ρ/(g·cm-3) A1/GPa B1/GPa n C1 m c0/(km·s-1) s Γ0 Q235 7.85 0.792 0.51 0.26 0.014 1.03 4.57 1.33 1.67 Cu 8.96 0.090 0.29 0.31 0.025 1.09 3.94 1.49 1.99 表 5 橡胶夹层和聚能壳体材料参数Table 5. Computational parameters for rubber interlayer and polymer shell材料 ρ/(g·cm-3) c0/(m·s-1) s Γ0 σb/MPa ε/% 橡胶 1.01 852 1.865 1.5 20 400 Teflon 2.15 1 680 1.82 0.59 30 450 3. 数值模拟结果及分析
图 5给出了射流与3种结构的反应装甲作用形态的数值模拟结果，其中t = 46 μs的全对称模型的数值模拟结果与X射线照片结果符合较好，验证了模型和参数的正确性。当t = 25 μs时，射流刚好穿透结构(a)橡胶复合装甲的背板，由于夹层的存在，射流头部在背板处发生了反射，此刻还未能引爆炸药；对于结构(b)和结构(c)，射流则已穿透面板，并引爆了夹层装药。钢板在冲击波和爆炸产物驱动作用下反向运动，后续射流在爆轰波的作用下局部产生了向上的弯曲。当t = 37μs时，射流头部穿透了背板，形成了逃逸射流，结构(b)最长，结构(a)次之，结构(c)最短，这是由于射流在侵彻结构(c)的背板时头部在复合层产生了反射，同时由于结构(c)的背板在运动过程中存在间隙，逃逸射流的后部与背板作用后会“挤入”间隙，因而逃逸射流长度最短。逃逸射流后部与结构(a)和结构(b)的背板作用后，会沿飞板孔壁接触面发生“滑移”，仍然可以逃逸。逃逸射流断裂后形成的颗粒在运动过程中长度发生改变、速度降低，最终3种结构的最长逃逸射流颗粒在触靶前运动速度分别为2.65、2.71和3.10 km/s，长度分别为8.5、12.0和6.5 mm。当t = 58 μs时，橡胶复合装甲两板之间的距离更加明显，射流后部经面板干扰后的偏折角无明显差别，当背板进一步飞离射流运动轴线后，就会失去对射流的作用，在后效靶表面的形成另一个损伤区域。
图 5 射流与3种结构的反应装甲在典型时刻的作用形态Figure 5. Results of interaction between jet and three structures of ERA at different times图 6为飞板的运动速度(vp)的计算结果，其中“F”和“B”分别表示面板和背板，“F-B”表示结构面板的背板(此时结构的面板为复合板)，前一个字母是相对于结构整体而言，后一个字母则是相对于复合板而言。由图 6可知，结构(b)钢面板和背板速度曲线基本相同，经过约4 μs的加速过程速度趋于平稳，终了速度为900 m/s。结构(a)和结构(c)钢板的加速历程基本相同，只是方向相反，钢飞板的终了速度约为920 m/s，而橡胶复合板的运动加速过程较复杂，与炸药相邻的钢板(内层板)存在着一个剧烈震荡过程，平均速度约为880 m/s；而外层钢板加速过程比较平稳，终了速度为1 050 m/s。橡胶复合板内、外层具有较大的速度差，其原因可能是炸药爆炸后在内层钢板中产生了较强的冲击波向橡胶层以及外层钢板传播，由于橡胶可压缩性较小，可作为良好的传压介质将冲击波传递给外层板，冲击波经外层板表面反射后产生拉伸波，拉伸波到达外层钢板与橡胶界面时由于不能承受拉应力而产生了“层裂”效应，使外层钢板获得了更高的速度，使逃逸射流长度减少，增加了其防护性能。
4. 结论
(1) 面密度基本相同条件下，复合板作为面板或背板的反应装甲防护性能优于钢反应装甲，其中橡胶复合板作为反应装甲背板时，防护性能最优。
(2) 爆炸驱动下橡胶复合板的外层钢板具有更高的速度，相比于钢反应装甲飞板提高约16%。
(3) 橡胶复合板界面效应和橡胶复合飞板的间隙可有效减小逃逸射流的长度。
-
图 3 v=1 200 m/s的装药爆炸后500 μs时的压力云图
Figure 3. Overpressure contour of initiated chargewith v=1 200 m/s in 500 μs
图 5 不同v时的f(Z)曲线和平均值及拟合曲线
Figure 5. Calculated curve of f(Z) in different v and their average value and fitted curve
图 6 不同v和Z时的f(θ)曲线和平均值及拟合曲线
Figure 6. Curve of f(θ) in different v and Z, and their average value and fitted curve
-
[1] 张光莹, 周旭, 黄咏政, 等.动爆冲击波特性分析方法研究[C]//第四届全国计算爆炸力学会议论文集.2008: 282-287. http://www.wanfangdata.com.cn/details/detail.do?_type=conference&id=7079475 [2] Henrych J, Abrahamson G R. The dynamics of explosion and its use[M]. New York: Elsevier Scientific Pub Co, 1979:218. [3] Baker W E. Explosions in air[M]. Austin: University of Texas Press, 1974:6-10. [4] Sadovskyi M A. Mechanical action of air shock waves of explosion, based on experimental data[M]. Moscow: Izd Akad Nauk SSSR, 1952:1-2. [5] 北京工业学院八系.爆炸及其作用[M].北京:工业出版社, 1978. [6] Izadifard R A, Foroutan M. Blastwave parameters assessment at different altitude using numerical simulation[J]. Turkish Journal of Engineering & Enviromental Sciences, 2010, 34(1):25-41. http://d.old.wanfangdata.com.cn/NSTLQK/NSTL_QKJJ0216335761/ [7] NUMERICS GmbH. SPPED user's Manual[Z]. 2012. [8] Lee E, Finger M, Collins W. JWL equation of state coeffients for high explosives: UCID-16189[R]. 1973. -
下载:
下载:
计量
- 文章访问数: 4455
- HTML全文浏览量: 1251
- PDF下载量: 473
- 被引次数: 0