基于拟流体模型的SPH新方法及其在弹丸超高速碰撞薄板中的应用

强洪夫; 范树佳; 陈福振; 刘虎

doi:10.11883/1001-1455(2017)06-0990-11

基于拟流体模型的SPH新方法及其在弹丸超高速碰撞薄板中的应用

doi: 10.11883/1001-1455(2017)06-0990-11

强洪夫¹,
范树佳^{1, 2, ,},
陈福振¹,
刘虎¹

1.
火箭军工程大学动力工程系，陕西西安 710025
2.
中国人民解放军96656部队，北京 100085

基金项目:

国家自然科学基金项目 51276192

详细信息

作者简介:
强洪夫(1963-)，男，博士，教授，博士生导师

通讯作者:
范树佳，fan_shu_jia@163.com

中图分类号: O389
计量
- 文章访问数: 4324
- HTML全文浏览量: 1336
- PDF下载量: 619
- 被引次数: 0
出版历程
- 收稿日期: 2016-07-09
- 修回日期: 2016-12-12
- 刊出日期: 2017-11-25

A new smoothed particle hydrodynamics method based on the pseudo-fluid model and its application in hypervelocity impact of a projectile on a thin plate

Qiang Hongfu¹,
Fan Shujia^{1, 2
, ,},
Chen Fuzhen¹,
Liu Hu¹

1.
Power Engineering Department, Rocket Force University of Engineering, Xi'an 710025, Shaanxi, China
2.
Unit 96656, PLA, Beijing 100085, China

摘要

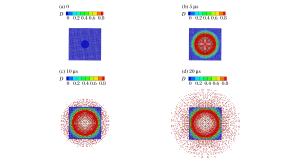
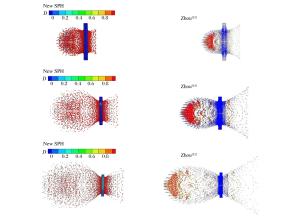
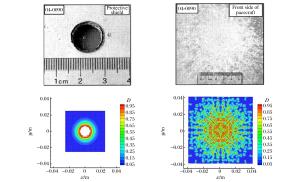
摘要: 引入颗粒动力学理论(拟流体模型)建立了适用于超高速碰撞的SPH新方法。将超高速碰撞中处于损伤状态的碎片等效为拟流体，在描述其运动过程中引入了碎片间相互作用和气体相对碎片的作用。采用该方法对球形弹丸超高速碰撞薄板形成碎片云的过程进行了数值模拟，得到了弹坑直径、外泡碎片云和内核碎片云的形状、分布，并与使用传统SPH方法、自适应光滑粒子流体动力学(ASPH)方法的模拟结果进行对比，结果显示：新方法在内核碎片云形状和分布上计算结果更加准确。同时对Whipple屏超高速碰撞问题进行了研究，分析了不同撞击速度下防护屏弹坑尺寸及舱壁损伤特性等特性，计算结果与实验吻合较好且符合Whipple防护结构的典型撞击极限曲线。
- SPH /
- 碎片云 /
- 超高速碰撞 /
- Whipple屏
Abstract: Based on the kinetic theory of granular flow (pseudo-fluid model), a new Smoothed Particle Hydrodynamics (SPH) algorithm suited for hyper velocity collision was presented in this paper. The damaged debris of the hyper velocity impact was equated with the pseudo-fluid and the effects of the debris' interaction and the effects of the gas on the formation process of the debris cloud were investigated. The new SPH algorithm was employed to simulate the 3D hyper velocity impact of an alloy projectile on thin target plates, and the numerical results of crater diameters, the structure and morphology characteristics of the debris cloud and the core debris cloud's shape and distribution were in good agreement with the experimental results. Compared with the simulations of the standard SPH and ASPH, the simulation of the new algorithm is more accurate in the core debris cloud's characteristics. Meanwhile, the hyper velocity impact of the Whipple shield problem was also simulated at different impact velocities. It was found that the crater diameters and the damage characteristics of the rear walls agree well with the experimental results, and that the simulation results are consistent with the typical ballistic limit curve of a Whipple shielding structure.
- smoothed particle hydrodynamics /
- debris cloud /
- hypervelocity impact /
- Whipple shield

HTML全文

图 1 算例模型结构

Figure 1. Experimental model

下载: 全尺寸图片幻灯片

图 2 不同SPH方法数值模拟结果与实验结果对比

Figure 2. Comparison of different SPH algorithm's simulation results and the experimental result

下载: 全尺寸图片幻灯片

图 3 铝弹超高速碰撞铝薄板俯视图

Figure 3. Top view of hypervelocity impact of projectile on thin plates

下载: 全尺寸图片幻灯片

图 4 SPH新方法与传统SPH方法计算结果对比

Figure 4. Comparison of the new SPH algorithm and traditional SPH algorithm's simulation results

下载: 全尺寸图片幻灯片

图 5 Whipple防护屏结构

Figure 5. Construction of Whipple shield

下载: 全尺寸图片幻灯片

图 6 撞击速度为5.29km/s时Whipple屏损伤情况

Figure 6. Damage characteristics of the Whipple shield at impact velocity of 5.29 km/s

下载: 全尺寸图片幻灯片

图 7 撞击速度为6.15km/s时Whipple屏损伤情况

Figure 7. Damage characteristics of the Whipple shield at impact velocity of 6.15 km/s

下载: 全尺寸图片幻灯片

表 1 本构模型参数

Table 1. Parameters of constitutive model

A/MPa	B/MPa	n	C	m	T_m/K	${\dot \varepsilon _0}$ /s^-1
300	426	0.34	0.015	1.0	775	1.0

C_V/(J·kg^-1·C^-1)		D₁	D₂	D₃	D₄	D₅
875		0.12	0.13	-1.5	0.0175	0

下载: 导出CSV

表 2 状态方程参数

Table 2. Parameters of state equation

ρ/(kg·m^-3)	a	b	A_T/GPa	B_T/GPa	α_T/GPa	β_T/GPa	E₀/(MJ·kg^-1)
2790	0.5	1.63	75	65	5	5	5

下载: 导出CSV

表 3 超高速碰撞数值模拟结果对比

Table 3. Comparison of high-velocity impact simulation results

方法	D₁	D₂	l/mm	w/mm	l/w	Δ/%
SPH新方法	29.4	33.7	105.7	81.4	1.30	6.5
Hiermaier实验^[10]	27.5	34.5	-	-	1.39	-
Hiermaier模拟^[10]	35.0	-	-	-	1.11	20.1
Liu模拟^[13]	28.9	-	105.1	86.1	1.22	12.2
Zhou模拟^[12]	31.6	35.3	102.8	75.5	1.36	2.2

下载: 导出CSV

表 4 LY12铝合金本构模型参数

Table 4. Parameters of LY12 aluminium alloy of constitutive model

A/MPa	B/MPa	n	C	m	T_m/K	${\dot \varepsilon _0}$ /s^-1
369	684	0.73	0.083	1.7	775	0.1

C_V/(J·kg^-1·C^-1)		D₁	D₂	D₃	D₄	D₅
875		0.13	0.13	-1.5	0.011	0

下载: 导出CSV

表 5 采用SPH新方法的数值模拟结果与实验结果比较

Table 5. Comparison of the new SPH algorithm and experimental results

编号	弹丸直径/mm	撞击角度/(°)	撞击速度/(km·s^-1)	防护屏弹孔直径/mm	中心损伤区域宽度/mm	舱壁损伤情况
实验04-0090	5	0	5.29	11.5	约50	3处剥落，无穿孔
仿真04-0090	5	0	5.29	12.1	54	无剥落、穿孔
实验04-0080	5	0	6.15	12.6	约50	无剥落、穿孔
仿真04-0080	5	0	6.15	12.6	62	无剥落、穿孔

下载: 导出CSV

参考文献(23)

[1]	Klinkrad H.Collision risk analysis for LEO[J]. Advances in Space Research, 1993, 13(2):105-112. http://www.sciencedirect.com/science/article/pii/0273117793905883
[2]	Whipple F L.Meteorites and space travel[J]. Astronomical Journal, 1947, 52(13):132-137. http://cn.bing.com/academic/profile?id=8269eae916575afbac913486ec4da33f&encoded=0&v=paper_preview&mkt=zh-cn
[3]	Piekutowski A J.Debris clouds produced by the hypervelocity impact of nonspherical projectiles[J]. International Journal of Impact Engineering, 2001, 26(1-10):613-624. doi: 10.1016/S0734-743X(01)00122-1
[4]	管公顺, 庞宝君, 哈跃, 等.铝合金Whipple防护结构高速撞击实验研究[J].爆炸与冲击, 2005, 25(5):461-466. doi: 10.3321/j.issn:1001-1455.2005.05.012 Guan Gongshun, Pang Baojun, Ha Yue, et al.Experimantal investigation of high-velocity impact on aluminum alloy Whipple shield[J]. Explosion and Shock Waves, 2005, 25(5):461-466. doi: 10.3321/j.issn:1001-1455.2005.05.012
[5]	Swift H F, Bamford R, Chen R.Designing space vehicle shields for meteoroid protection a new analysis[J]. Advances in Space Research, 1983, 2(12):219-234. http://www.sciencedirect.com/science/article/pii/0273117782903118
[6]	Lucy L B.A numerical approach to the testing of the fission hypothesis[J]. Astronomical Journal, 1977, 82:1013-1024. doi: 10.1086/112164
[7]	Gingold R A, Monaghan J J.Smoothed particle hydrodynamics:theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181(3):375-389. doi: 10.1093/mnras/181.3.375
[8]	Libersky L D, Petscheck A G.Smoothed particle hydrodynamics with strength of materials[C]//Trease H, Fritts J, Crowley W.Proceedings of The Next Free Lagrange Conference.Springer Verlag, New York, 1991, 395: 248-257.
[9]	Johnson G R, Petersen E H, Stryk R A.Incorporation of an SPH option into the EPIC code for a wide range of high velocity impact computations[J]. International Journal of Impact Engineering, 1993, 14(1-4):385-394. doi: 10.1016/0734-743X(93)90036-7
[10]	Hiermaier S, Könke D, Stilp A J, et al.Computational simulation of the hypervelocity impact of Al-spheres on thin plates of different materials[J]. International Journal of Impact Engineering, 1997, 20(1-5):363-374. doi: 10.1016/S0734-743X(97)87507-0
[11]	徐金宏, 汤文辉, 罗永.光滑粒子模拟法在超高速碰撞现象中的应用[J].爆炸与冲击, 2006, 26(1):53-58. doi: 10.3321/j.issn:1001-1455.2006.01.009 Xu Jinhong, Tang Wenhui, Luo Yong.Applications of the smoothed particle hydrodynamics method to hypervelocity impact simulations[J]. Explosion and Shock Waves, 2006, 26(1):53-58. doi: 10.3321/j.issn:1001-1455.2006.01.009
[12]	Zhou C E, Liu G R, Lou K Y.Three-dimensional penetration simulation using smoothed particle hydrodynamics[J]. International Journal of Computational Methods, 2007, 4(4):671-691. doi: 10.1142/S0219876207000972
[13]	Liu G R, Liu M B.Smoothed particle hydrodynamics:a meshfree particle method[M]. Singapore:Word Scientific Publishing Co.Pte.Ltd., 2003.
[14]	陈福振, 强洪夫, 高巍然.风沙运动问题的SPH-FVM耦合方法数值模拟[J].物理学报, 2014, 63(13):130202. doi: 10.7498/aps.63.130202 Chen Fuzhen, Qiang Hongfu, Gao Weiran.Simulation of aeolian sand transport with SPH-FVM coupled method[J]. Acta Physica Sinica, 2014, 63(13):130202. doi: 10.7498/aps.63.130202
[15]	陈福振, 强洪夫, 高巍然.气-粒两相流传热问题的光滑离散颗粒流体动力学方法数值模拟[J].物理学报, 2014, 63(23):230206. doi: 10.7498/aps.63.230206 Chen Fuzhen, Qiang Hongfu, Gao Weiran.Numerical simulation of heat transfer in gas-particle two-phase flow with smoothed discrete particle hydrodynamics[J]. Acta Physica Sinica, 2014, 63(23):230206. doi: 10.7498/aps.63.230206
[16]	陈福振, 强洪夫, 高巍然.燃料爆炸抛撒成雾及其爆轰过程的SDPH方法数值模拟研究[J].物理学报, 2015, 64(11):110202. doi: 10.7498/aps.64.110202 Chen Fuzhen, Qiang Hongfu, Gao Weiran.Numerical simulation of fuel dispersal into cloud and its combustion and explosion with smmoothed discrete particle hydrodymamics[J]. Acta Physica Sinica, 2015, 64(11):110202. doi: 10.7498/aps.64.110202
[17]	Johnson G R, Cook W H.A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures[C]//Proceedings of the Seventh International Symposium on Ballistics.Hague, Netherlands, 1983: 541-547 https://www.scirp.org/(S(351jmbntvnsjt1aadkposzje))/reference/ReferencesPapers.aspx?ReferenceID=1224970
[18]	李春雷.2A12铝合金本构关系实验研究[M].哈尔滨:哈尔滨工业大学, 2006.
[19]	费思聪, 孙秦.铝合金的J-C失效参数标定与仿真分析[J].计算机仿真, 2013, 30(9):46-50. doi: 10.3969/j.issn.1006-9348.2013.09.011 Fei Sicong, Sun Qin.Investigation on parameters calibration for the J-C failure model of aluminum alloy[J]. Computer Simulation, 2013, 30(9):46-50. doi: 10.3969/j.issn.1006-9348.2013.09.011
[20]	迟润强.弹丸超高速撞击薄板碎片云建模研究[D].哈尔滨: 哈尔滨工业大学, 2010.
[21]	柳森, 李毅, 黄洁, 等.用于验证数值模拟仿真的Whipple屏超高速撞击试验结果[J].宇航学报, 2005, 26(4):505-508. doi: 10.3321/j.issn:1000-1328.2005.04.024 Liu Sen, Li Yi, Huang Jie, et al.Hypervelocity impact test results of Whipple shield for the validation of numerical simulations[J]Journal of Astronautics, 2005, 26(4):505-508. doi: 10.3321/j.issn:1000-1328.2005.04.024
[22]	侯日立, 周平, 彭建祥冲击波作用下LY12铝合金结构损伤的数值模拟[J].爆炸与冲击, 2012, 32(5):470-474. doi: 10.3969/j.issn.1001-1455.2012.05.004 Hou Rili, Zhou Ping, Peng Jianxiang, Numerical simulation of shock damage of LY12 aluminium alloy structure[J]. Explosion and Shock Waves, 2012, 32(5):470-474. doi: 10.3969/j.issn.1001-1455.2012.05.004
[23]	徐金中.基于SPH方法的空间碎片超高速碰撞特性及其防护结构设计研究[D].长沙: 国防科学技术大学, 2008.