PTFE材料在高应变率冲击下的力学性能

李顺平; 冯顺山; 薛再清; 涂建

doi:10.11883/1001-1455(2017)06-1046-05

PTFE材料在高应变率冲击下的力学性能

doi: 10.11883/1001-1455(2017)06-1046-05

李顺平^{1, 2,},
冯顺山²,
薛再清¹,
涂建¹

1.
北京航天长征飞行器研究所, 北京 100076
2.
北京理工大学, 北京 100081

基金项目:

国家自然科学基金项目 11202028

高等学校博士学科点专项科研基金项目 20121101110012

详细信息

作者简介:
李顺平(1986—)，女，博士后，lishp@14.calt.casc

中图分类号: O347.3
计量
- 文章访问数: 4468
- HTML全文浏览量: 1405
- PDF下载量: 441
- 被引次数: 11
出版历程
- 收稿日期: 2016-04-25
- 修回日期: 2016-07-31
- 刊出日期: 2017-11-25

Mechanical properties of PTFE at high strain rate

1.
Beijing Institute of Space Long March Vehicle, Beijing 100076, China
2.
Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 聚四氟乙烯(PTFE)在高速碰撞或者爆炸加载时的应变率可高达10⁶ s^-1，高应变率下PTFE材料的力学响应会对其材料性能产生较大影响。本文中采用压剪炮试验系统(PSPI)测试了PTFE材料在高应变率(10⁵~10⁶ s^-1)下的压缩力学性能，实验中碳化钨(WC)飞片板以一定速度撞击由前靶板、试件和后靶板组成的三明治结构，并采用激光干涉仪记录后靶板自由面的速度变化。对实验结果处理后得到该PTFE材料的应力应变数值，并拟合得到应力应变曲线。本研究对PTFE/金属复合材料制成的动能侵彻体强度及其冲击碎化机理的分析具有指导意义。
- 聚四氟乙烯(PTFE) /
- 高应变率 /
- 压剪炮试验系统(PSPI) /
- 应力应变曲线
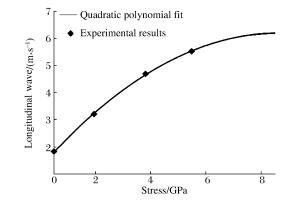
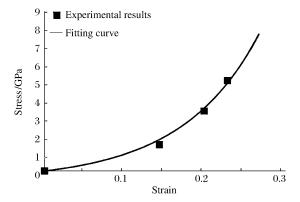
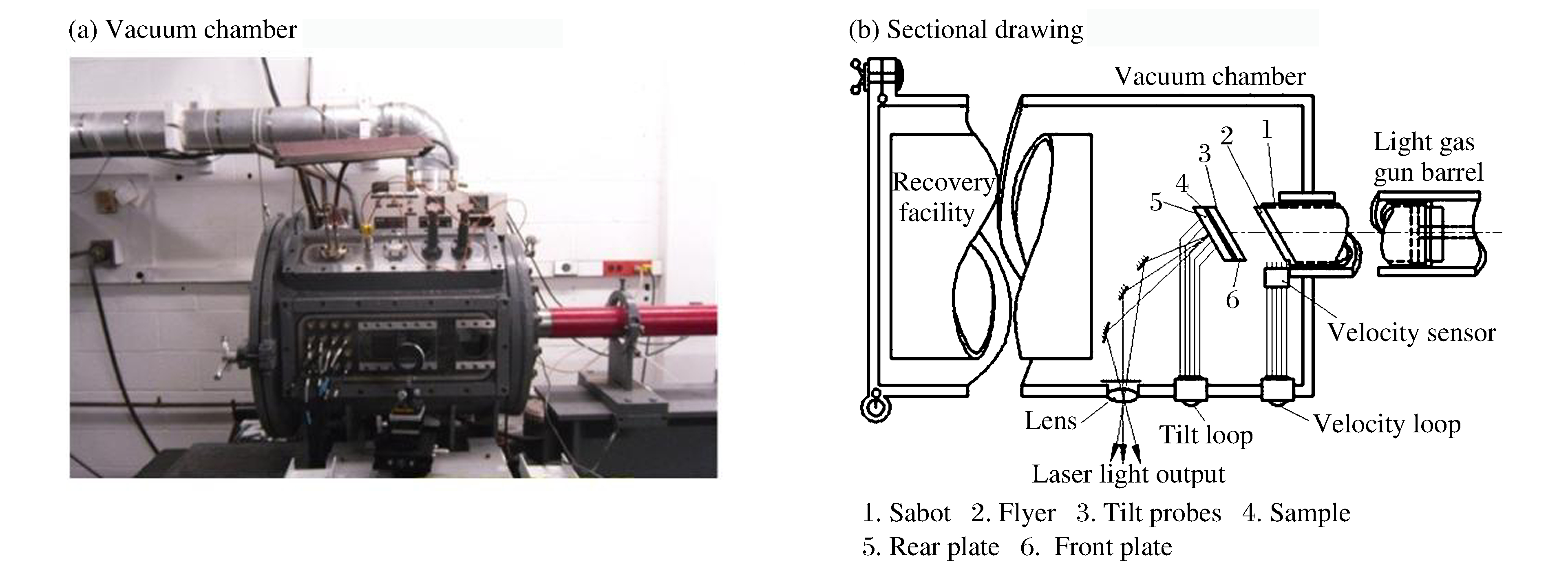
Abstract: The mechanical properties of polyetrafluoroethylene (PTFE), which is being used increasingly in diverse applications owing to its many attractive properties, are important for applications involving either high-velocity impact or blast loading at very high strain rates (of the order of 10⁶ s^-1). In this work, for high strain rates of 10⁵~10⁶ s^-1, the PTFE dynamic pressure experiment was conducted using the pressure-shear plate-impact (PSPI) facility in which a tungsten-carbide (WC) flyer impacted a target assembly consisting of a thin PTFE plate sandwiched between two hard (elastic) WC plates. The velocity at the free surface of the target assembly was measured using the laser interferometry, an effective method was adopted to analyze the experimental results to obtain the values of the stress and strain at four points, and the stress strain relationship was fitted. The investigation has significance for the analysis of the strength and impact crushing performance of PTFE/metal reactive fragments.
- polyetrafluoroethylene (PTFE) /
- high strain rate /
- pressure-shear plate-impact (PSPI) /
- stress-strain curve

HTML全文

图 1 PSPI试验系统真空密闭测试箱及其剖面图

Figure 1. Vacuum chamber and its sectional drawing of PSPI facility setup

下载: 全尺寸图片幻灯片

图 2 后靶板自由面法向速度变化

Figure 2. Normal velocity of free surface of rear plate vs. time of PSPI test

下载: 全尺寸图片幻灯片

图 3 纵波在飞片板、前靶板和后靶板以及试件中的传播示意图

Figure 3. t-x diagram of longitudinal waves propagation in plates and sample

下载: 全尺寸图片幻灯片

图 4 声速随应力的变化

Figure 4. Longitudinal wave speed vs. pressure

下载: 全尺寸图片幻灯片

图 5 4 mm厚PTFE材料在10⁵~10⁶ s^-1应变率下的应力应变曲线

Figure 5. Stress-strain profile for PTFE film of 4 mm thickness across strain rate 10⁵~10⁶ s^-1 of PSPI test

下载: 全尺寸图片幻灯片

表 1 实验参数

Table 1. Experimental parameters for PSPI test

实验号	h/mm	h_front/mm	h_rear/mm	h_flyer/mm	Ø/mm	靶板材料	v₀/(m·s^-1)	倾斜角/rad
SL1301	0.4	4.016	4.026	4.021	50	WC#504	186.7	＜0.7

下载: 导出CSV

参考文献(8)

[1]	Chou S C, Robertson K D, Rainey J H. The effect of strain rate and heat developed during deformation on the stress-strain curve of plastics[J]. Experimental Mechanics, 1973, 13(10):422-432. doi: 10.1007/BF02324886
[2]	Brown E N, Willms R B, Gray Ⅲ G T, et al. Influence of molecular conformation on the constitutive response of polyethylene: a comparison of HDPE, UHMWPE, and PEX[J]. Experimental Mechanics, 2007, 47(3):381-393. doi: 10.1007/s11340-007-9045-9
[3]	Walley S M, Field J E. Strain rate sensitivity of polymers in compression from low to high rates[J]. DYMAT Journal, 1994, 1(3):211-227.
[4]	Rae P J, Dattelbaum D M. The properties of poly (tetrafluoroethylene) (PTFE) in compression[J]. Polymer, 2004, 45(22):7615-7625. doi: 10.1016/j.polymer.2004.08.064
[5]	Khan A, Zhang H. Finite deformation of a polymer: experiments and modeling[J]. International Journal of Plasticity, 2001, 17(9):1167-1188. doi: 10.1016/S0749-6419(00)00073-5
[6]	Jennifer L J, Clive R S. Compressive properties of extruded polytetrafluoroethylene[J]. Polymer, 2007, 48(14):4184-4195. doi: 10.1016/j.polymer.2007.05.038
[7]	Zerilli F J, Armstrong R W. A constitutive equation for the dynamic deformation behavior of polymers[J]. Journal of Materials Science, 2007, 42(12):4562-4574. doi: 10.1007/s10853-006-0550-5
[8]	Kim K S, Rodney J C, Prashant Kumar. A combined normal- and transverse-displacement interferometer with an application to impact of ycutquartz[J]. Journal of Applied Physics, 1977, 48(10):4132. doi: 10.1063/1.323448

施引文献

期刊类型引用(6)

1.	吴琳，吕亚茹，张申，丁思超. 砂土SHPB冲击试验与数值模拟研究进展及问题探讨. 岩土力学. 2024(11): 3461-3480 . 百度学术
2.	郭瑞奇，李江南，马林建，欧灿，许鑫. CF/SSF增强珊瑚砂水泥砂浆微观结构分析及动态劈裂拉伸试验研究. 爆炸与冲击. 2024(11): 77-89 . 本站查看
3.	郑志豪，任辉启，龙志林，郭瑞奇，蔡洋，黎智健. PP/CF增强珊瑚砂水泥基复合材料冲击压缩力学性能研究. 爆炸与冲击. 2022(07): 61-73 . 本站查看
4.	李斌，朱志武，李涛. 冻融循环冻土的冲击动态力学性能. 爆炸与冲击. 2022(09): 166-180 . 本站查看
5.	陈涛，吴健安，马林建，耿汉生，董璐. 珊瑚砂静动态力学特性及应力波传播规律研究进展. 土工基础. 2022(06): 861-867 . 百度学术
6.	董凯，任辉启，阮文俊，黄魁，步鹏飞. 爆炸冲击下珊瑚砂动态本构模型. 爆炸与冲击. 2021(04): 88-99 . 本站查看