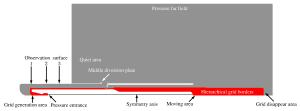
Influence of thermal shock mechanism and thermal environment on concentric canister launcher
-
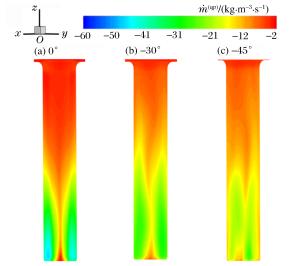
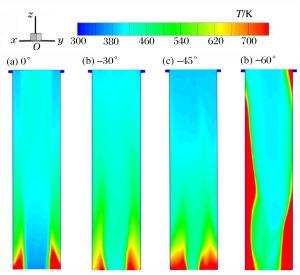
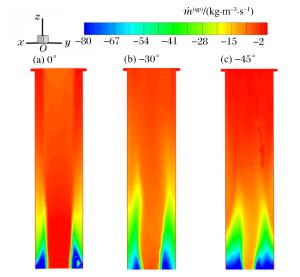
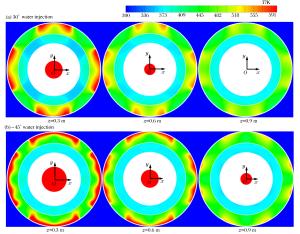
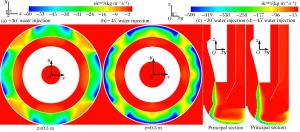
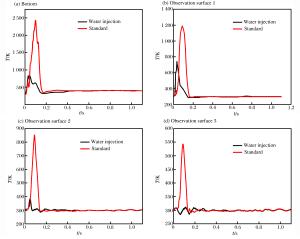
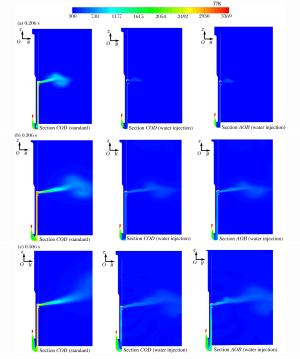
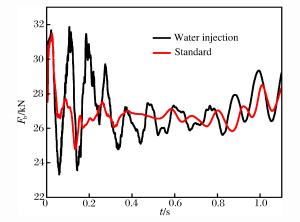
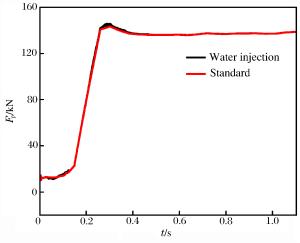
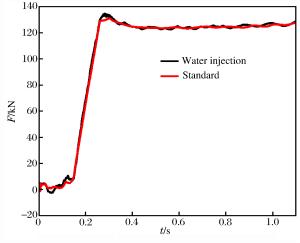
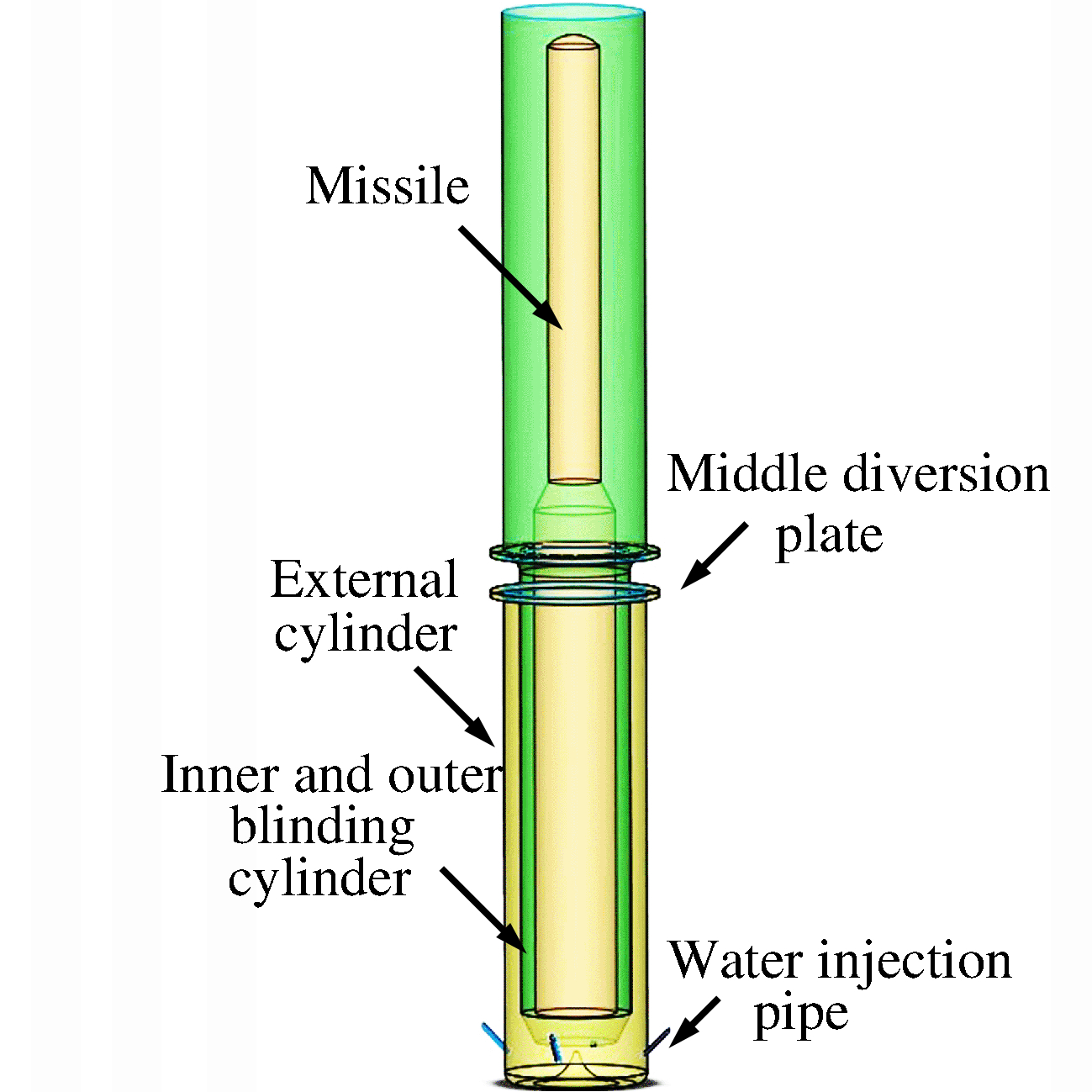
摘要: 针对路基同心筒自力发射整体热环境恶劣的问题，依托弹性变形和域动分层相结合的动网格技术，基于均质多相流理论并耦合液态水专用汽化求解程序，建立在发射筒底部注水的三维气液两相流体动力学模型；以火箭发动机自由射流注水实验为基础，验证汽化程序三维计算的可靠性与有效性；通过瞬态数值计算，讨论筒底注水角度对导弹、内外筒热环境和导弹载荷特性的影响规律。分析表明：发射筒内发生了显著的汽化反应；导弹及发射系统总体热环境得到了显著改善，实现了发射系统持续降温的目的；在筒底注水后，弹底的附加推力及火箭发动机的推力有一定增加，随着注水量的减少，注水对导弹载荷的影响越来越弱。Abstract: Based on the homogeneous multiphase theory and vaporization solving program of liquid water, the three-dimensional model of the gas-liquid two-phase fluid dynamics for new concentric canister launcher (CCL) self-launching system was built using the dynamic mesh technology of spring-based smoothing method and laying-based zone moving method. The reliability and validity of the three dimensional calculation of the vaporization program were verified by the experiment of injecting liquid water into the free rocket jet. Transient numerical calculation was carried out, and the influences of the water injection angle on the thermal environment of the launching system and the load characteristics of the missile were discussed. Analysis shows that obvious vaporization reaction occurred in the launch tube, in the -30 degree water injection scheme, the gas-liquid two-phase mixing was sufficient, and the transverse cooling range of the cylinder was more uniform; the overall thermal environment of the missile and launching system was improved significantly, and the goal of continuously cooling the launching system was achieved; after the water injection at the cylinder bottom, the additional thrust and the thrust of the rocket engine increased, with the decrease of the water injection quantity, and the influence of the water injection on the missile load was increasingly weaker.
-
图 2 路基同心筒自力发射动网格模型示意图
Figure 2. Dynamic-mesh model for new concentric canister launcher system
图 3 各注水角度内筒外壁面温度
Figure 3. Temperature of outer wall for inner tube at different injection angles
图 4 各注水角度内筒外壁面汽化率
Figure 4. Vaporization rate of outer wall for inner tube at different injection angles
图 5 各注水角度外筒内壁面温度
Figure 5. Temperature of inner wall for outer tube at different injection angles
图 6 各注水角度外筒内壁面汽化率
Figure 6. Vaporization rate of inner wall for outer tube at different injection angles
图 7 两种注水角度不同截面温度分布
Figure 7. Temperature distribution of different section for two kinds of injection angle
图 8 两种注水角度不同截面汽化率
Figure 8. The vaporization rate of different section for two kinds of injection angle
表 1 压力与水的饱和温度和汽化潜热数据关系
Table 1. Relation between pressure and water saturation temperature and latent heat of vaporization
p
/MPaTsat
/KQq
/(kJ·kg-1)0.001 279.98 2484.5 0.002 290.51 2459.8 0.003 297.98 2444.2 0.009 316.79 2397.5 0.010 318.83 2392.6 0.015 327.00 2372.9 0.050 354.35 2305.4 0.060 358.95 2293.7 0.070 362.96 2283.4 0.080 366.51 2274.3 0.090 369.71 2265.9 0.100 372.63 2258.2 0.250 400.43 2181.8 0.300 406.54 2164.1 0.350 411.88 2148.2 0.700 437.96 2065.8 0.800 443.42 2047.5 0.900 448.36 2030.4 1.000 452.88 2014.4 1.100 457.06 1999.3 1.200 460.96 1985.0 1.800 480.10 1910.5 1.900 482.79 1899.6 2.000 485.37 1888.8 3.000 506.84 1793.5 3.500 515.54 1751.5 4.000 523.33 1711.9 5.000 536.33 1638.2 6.000 548.56 1569.4 7.000 558.80 1503.7 13.000 603.81 1129.4 14.000 609.63 1065.5 15.000 615.12 990.4 20.000 638.71 585.0 21.000 642.79 448.0 22.000 646.68 184.8 
下载: 导出CSV
表 2 观测点温度
Table 2. Temperature at observation points
观测点 T/K ε/% 实验[21] 计算 A 545 590 8.26 B 535 570 6.54 C 520 550 5.77 D 515 535 3.74
下载: 导出CSV
表 3 注水方案对应参数
Table 3. Corresponding parameters of water injection project
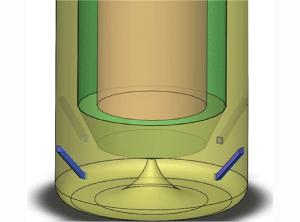
方案 n α/(°) β/(°) $ {{{\mathit{\dot{m}}}}_{\rm{w}}}$ v/(m·s-1) cosβcosα cosβsinα sinβ 1 4 45 0 56.00 35.000 -0.707 -0.707 0.000 2 4 45 -30 56.00 40.415 -0.612 -0.612 -0.500 3 4 45 -45 56.00 49.498 -0.500 -0.500 -0.707 4 4 45 -60 56.00 70.000 -0.353 -0.353 -0.866
下载: 导出CSV
-
[1] 杨风波, 马大为, 杨帆.高压弹射装置内弹道建模与计算[J].兵工学报, 2013, 34(5):527-534. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bigo201305003&dbname=CJFD&dbcode=CJFQYANG Fengbo, MA Dawei, YANG Fan. Interior ballistics modeling and calculation of high-pressure ejection device[J]. Acta Armamentarii, 2013, 34(5):527-534. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bigo201305003&dbname=CJFD&dbcode=CJFQ [2] 张仁军, 鲍福延.两种不同注水方式的燃气蒸汽式发射系统内弹道性能比较[J].固体火箭技术, 2005, 28(1):5-9. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gthj200501001&dbname=CJFD&dbcode=CJFQZHANG Renjun, BAO Fuyan. Comparison of internal ballistic properties between gas and steam launching system in two different modes of water injection[J]. Journal of Solid Rocket Technology, 2005, 28(1):5-9. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gthj200501001&dbname=CJFD&dbcode=CJFQ [3] 邵立武, 姜毅, 马艳丽, 等.新型舰载同心筒发射过程流场研究[J].导弹与航天运载技术, 2011(4):54-58. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ddyh201104016&dbname=CJFD&dbcode=CJFQSHAO Liwu, JIANG Yi, MA Yanli, et al. Launching process of the new type ship-borne concentric canister launcher[J]. Missiles and Space Vehicles, 2011(4):54-58. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ddyh201104016&dbname=CJFD&dbcode=CJFQ [4] 杨风波, 马大为, 任杰, 等.新型湿式发射对同心筒瞬态热冲击的影响机理研究[J].固体火箭技术, 2014, 37(3):301-306. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bzcj201801005&dbname=CJFD&dbcode=CJFQYANG Fengbo, MA Dawei, REN Jie, et al. Research on flow field mechanism and thermal environment of a new vehicle-carried concentric canister launcher[J]. Journal of Solid Rocket Technology, 2014, 37(3):301-306. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bzcj201801005&dbname=CJFD&dbcode=CJFQ [5] 杨风波, 马大为, 薛新宇, 等.新型路基同心筒热冲击机理与热环境影响因子[J].爆炸与冲击, 2016, 36(2):153-160. http://www.bzycj.cn/CN/abstract/abstract9576.shtmlYANG Fengbo, MA Dawei, XUE Xinyu, et al. Study on thermal shock mechanism and thermal environment effecting factors of a new concentric canister launcher[J]. Explosion and Shock Waves, 2016, 36(2):153-160. http://www.bzycj.cn/CN/abstract/abstract9576.shtml [6] 姜毅, 郝继光, 傅德彬, 等.新型"引射同心筒"垂直发射装置理论及试验研究[J].宇航学报, 2008, 29(1):236-241. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yhxb200801042&dbname=CJFD&dbcode=CJFQJIANG Yi, HAO Jiguang, FU Debin, et al. Study on theory and test of a new type concentric canister with jet flow vertical launcher[J]. Journal of Astronautics, 2008, 29(1):236-241. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yhxb200801042&dbname=CJFD&dbcode=CJFQ [7] 于勇, 母云涛.新型变截面同心筒发射装置及其热环境气动原理研究[J].宇航学报, 2013, 34(9):1281-1287. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yhxb201309016&dbname=CJFD&dbcode=CJFQYU Yong, MU Yuntao. Configuration and gas dynamic dynamics analysis for a new variable cross-section concentric canister launcher[J]. Journal of Astronautics, 2013, 34(9):1281-1287. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yhxb201309016&dbname=CJFD&dbcode=CJFQ [8] 马艳丽, 姜毅, 王伟臣, 等.湿式同心筒自力垂直热发射技术降温效果研究[J].弹道学报, 2010, 22(4):89-93. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ddxb201004023&dbname=CJFD&dbcode=CJFQMA Yanli, JIANG Yi, WANG Weichen, et al. Research on launching process cooling effect of wet concentric canister launcher[J]. Journal of Ballistics, 2010, 22(4):89-93. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=ddxb201004023&dbname=CJFD&dbcode=CJFQ [9] 郭锦烈.两相与多相流动力学[M].西安:西安交通大学出版社, 2002. [10] MAMORU I. Themo-fluid dynamic theory of two-phase flow[M]. Paris: Eyrolles, 2005. [11] WEN C Y, YU T H. Mechanics of fluidization[J]. The Chemical Engineering Progress Symposium Series, 1966, 62(1):100-111. http://www.mendeley.com/catalog/mechanics-fluidization/ [12] 李萍, 丁珏, 翁培奋, 等.两种颗粒湍流扩散模型数值模拟气液两相流泄露扩散的比较[J].爆炸与冲击, 2005, 25(6):541-546. http://www.bzycj.cn/CN/abstract/abstract9392.shtmlLI Ping, DING Jue, WENG Peifen, et al. A numerical simulation on liquid gas two phase leakage dispersion by using two partical turbulent models[J]. Explosion and Shock Waves, 2005, 25(6):541-546. http://www.bzycj.cn/CN/abstract/abstract9392.shtml [13] MANNINEN M, Taivassalo V, Lallio S. On the mixture model for multiphase flow[M]. VTT Publications 288, 1996. [14] 王汉平, 余文辉, 魏建峰.潜射模拟弹筒口压力场仿真[J].兵工学报, 2009, 30(8):1009-1013. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bigo200908001&dbname=CJFD&dbcode=CJFQWANG Hanping, YU Wenhui, WEI Jianfeng, et al. Simulation of pressure field near canister outlet for underwater launched emulated missile[J]. Acta Armamentarii, 2009, 30(8):1009-1013. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=bigo200908001&dbname=CJFD&dbcode=CJFQ [15] 曹嘉怡, 鲁传敬, 李杰.水下超声速燃气射流动力学特性研究[J].水动力学研究与进展:A辑, 2009, 24(5):1-10. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=sdlj200905009&dbname=CJFD&dbcode=CJFQCAO Jiayi, LU Chuanjin, LI Jie. Research on dynamic characteristics of underwater superasonic gas jets[J]. Journal of Hydrodynamics, 2009, 24(5):1-10. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=sdlj200905009&dbname=CJFD&dbcode=CJFQ [16] VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamic: The finite volume method[M]. Berlin: Springer Heidelberg, 2007. [17] 王志健, 杜佳佳.动网格在固体火箭发动机非稳态工作过程中的应用[J].固体火箭技术, 2008, 31(4):350-353. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gthj200804013&dbname=CJFD&dbcode=CJFQWANG Zhijian, DU Jiajia. Application of dynamic mesh to unsteady burning of solid rocket motor[J]. Journal of Solid Rocket Technology, 2008, 31(4):350-353. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=gthj200804013&dbname=CJFD&dbcode=CJFQ [18] ORSZAG S A, YAKHOT V, FLANNEY W S. Renormalization group modeling and turbulence[J]. Journal of Scientific Computing, 1986, 1(1):3-51. doi: 10.1007/BF01061452 [19] 陈则韶.高等工程热力学[M].北京:高等教育出版社, 2008. [20] 周帆, 姜毅, 郝继光.火箭发动机尾焰流场注水降温效果初探[J].推进技术, 2012, 33(2):249-252. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tjjs201202015ZHOU Fan, JIANG Yi, HAO Jiguang. Exploring on cooling effect of water injection on rocket motor exhaust[J]. Journal of Propulsion Technology, 2012, 33(2):249-252. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=tjjs201202015 -
计量
- 文章访问数: 8586
- HTML全文浏览量: 1908
- PDF下载量: 109
- 被引次数: 0