Analysis of axial vibration frequency for projectile structure in penetration
-
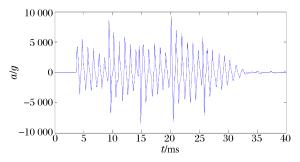
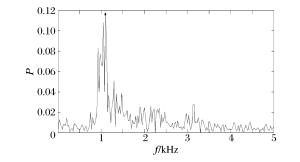
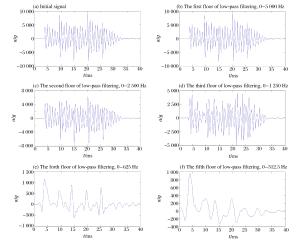
摘要: 加速度传感器测试弹体加速度历程时,测试结果包含由于目标阻碍导致弹体减速的过载加速度和弹体结构振动引起的加速度。通过将弹体简化为均匀的长直圆杆,从理论上分析弹体纵向振动的频率特性。利用ANSYS建立了弹体有限元模型,通过模态分析得到了弹体纵向振动对应的固有频率及固有振型,并对弹体进行谐响应分析,一阶纵向振动固有频率的理论值、模态分析与谐响应分析的模拟结果都在1 200 Hz。利用Fourier变换和小波分析,对加速度传感器测试数据的频率特性进行了分析,Fourier变换得到的信号功率谱峰值在1 114 Hz,与理论计算结果、模拟结果都能较好吻合。Abstract: In the measurement of a projectile's acceleration history using an acceleration transducer, the results achieved contain the acceleration resulting from the hindrance of a target that decelerates the projectile and the acceleration resulting from the structural vibration of the missile. In this study, a simple model was established simplifying the projectile as a long straight round bar and analyses the frequency characteristics of the axial vibration of a projectile. A finite element model of the projectile was built using ANSYS to solve the natural frequency and mode of the projectile via modal analysis, then the harmonic response analysis about the projectile was conducted. The theoretical results and simulated results were quite consistent, both about 1 200 Hz. The frequency characteristics of the actual acceleration signal obtained from the target experiment were analyzed via the Fourier transform and wavelet analysis. The peak value of the signal power density spectrum was at 1 114 Hz, consistent with both the theoretical value and the simulated result.
-
表 1 材料模型参数
Table 1. Material parameter in simulation
材料 ρ/(kg·m-3) E/GPa ν 弹壳 7 800 210 0.28 装药 1 800 30 0.30 压紧环 7 800 210 0.28 表 2 模态分析与谐响应分析结果与理论值的比较
Table 2. Comparison of simulation results with theoretical values
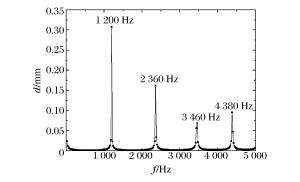
阶数 f/Hz δf/% 简化模型 模态分析 谐响应分析 模态分析 谐响应分析 1 1 235.4 1 198.4 1 200 3.0 2.9 2 2 470.8 2 363.4 2 360 4.3 4.5 3 3 706.2 3 451.0 3 460 6.9 6.6 4 4 941.6 4 386.6 4 380 11.2 11.4 -
[1] 赵海峰, 张亚, 李世忠, 等.侵彻弹体频率特性分析及过载信号处理[J].中国机械工程, 2015, 26(22):3034-3039. doi: 10.3969/j.issn.1004-132X.2015.22.009ZHAO Haifeng, ZHANG Ya, LI Shizhong, et al. Frequency characteristics analysis and overload signal process of penetration projectile[J]. China Mechanical Engineering, 2015, 26(22):3034-3039. doi: 10.3969/j.issn.1004-132X.2015.22.009 [2] 宋萍, 李科杰.硬目标侵彻武器高冲击试验和高过载传感器技术国外发展概况[J].测控技术, 2002, 21(增刊1):30-32. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ckjs2002z1012SONG Ping, LI Kejie. Development of the technique of high shock test on hard-target penetration weapons and high-g accelerometer at broad[J]. Measurement & Control Technology, 2002, 21(suppl 1):30-32. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=ckjs2002z1012 [3] RASHKOVSKA A, TROBEC R, DEPOLLI M, et al. Time and frequency analysis of non-uniform sampling[C]//MIPRO, Proceedings of the 33rd International Convention. 2010: 236-240. [4] 徐鹏, 祖静, 范锦彪.高g值侵彻加速度测试及其相关技术研究进展[J].兵工学报, 2011, 32(6):739-745. http://xueshu.baidu.com/s?wd=paperuri%3A%28dc989779149b2bc362aeeb7b73b3f62a%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fkns.cnki.net%2FKCMS%2Fdetail%2Fdetail.aspx%3Ffilename%3Dbigo201106018%26dbname%3DCJFD%26dbcode%3DCJFQ&ie=utf-8&sc_us=860878574745771933XU Peng, ZU Jing, FAN Jinbiao. Research development of high g penetration acceleration test and its correlative technology[J]. Acta Armamentarii, 2011, 32(6):739-745. http://xueshu.baidu.com/s?wd=paperuri%3A%28dc989779149b2bc362aeeb7b73b3f62a%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fkns.cnki.net%2FKCMS%2Fdetail%2Fdetail.aspx%3Ffilename%3Dbigo201106018%26dbname%3DCJFD%26dbcode%3DCJFQ&ie=utf-8&sc_us=860878574745771933 [5] ZHANG Wendong, CHEN Lujiang, XIONG Jijun. Ultra-high g deceleration-time measurement for the penetration into steel target[J]. International Journal of Impact Engineering, 2007, 34(3):436-447. doi: 10.1016/j.ijimpeng.2006.01.008 [6] 赵小龙, 马铁华, 徐鹏, 等.弹丸侵彻混凝土加速度信号测试及分析[J].爆炸与冲击, 2014, 34(3):347-353. doi: 10.11883/1001-1455(2014)03-0347-07ZHAO Xiaolong, MA Tiehua, XU Peng, et al. Acceleration signal test and analysis for projectile penetrating into concrete[J]. Explosion and Shock Waves, 2014, 34(3):347-353. doi: 10.11883/1001-1455(2014)03-0347-07 [7] HAO H, LI X, SUN Y. Projectile structural response frequency characteristics analysis method in penetration process[J]. Journal of Vibration Measurement & Diagnosis, 2013, 1997(16):7-11. doi: 10.1142/S0219455412500241?queryID=%24%7BresultBean.queryID%7D [8] 黄家蓉, 刘瑞朝, 何翔, 等.侵彻过载测试信号的数据处理方法[J].爆炸与冲击, 2009, 29(5):555-560. doi: 10.11883/1001-1455(2009)05-0555-06HUANG Jiarong, LIU Ruichao, HE Xiang, et al. A new data processing technique for measured penentration overloads[J]. Explosion and Shock Waves, 2009, 29(5):555-560. doi: 10.11883/1001-1455(2009)05-0555-06 [9] ZHANG Q. Applications of FEM and lanczos algorithm in modal analysis of slender missile[J]. Journal of Projectile Rocket & Guidance, 2007, 27(4):61-63. https://www.sciencedirect.com/science/article/pii/095605219190023X [10] 王秋萍, 张虎, 吴迎春.金属杆中纵固有频率的研究[J].声学与电子工程, 2005, 24(8):144-147. http://www.docin.com/p-1135857535.htmlWANG Qiuping, ZHANG Hu, WU Yingchun. Study of longitudinal vibrating natural frequency of metallic rod[J]. Acoustics and Electronics Engineering, 2005, 24(8):144-147. http://www.docin.com/p-1135857535.html -







 下载:
下载: