基于耦合算法的三维复杂结构冲击动力学特性

初文华; 朱东俊; 梁德利; 封峰; 韦斯俊

doi:10.11883/bzycj-2016-0283

基于耦合算法的三维复杂结构冲击动力学特性

doi: 10.11883/bzycj-2016-0283

初文华^{1, 2, 3,},
朱东俊⁴,
梁德利⁵,
封峰⁶,
韦斯俊⁴

1.
上海海洋大学海洋科学学院, 上海 201306
2.
国家远洋渔业工程技术研究中心, 上海 201306
3.
大洋渔业资源可持续开发教育部重点实验室, 上海 201306
4.
天合汽车研发上海有限公司, 上海 200233
5.
空间物理重点实验室, 北京 100076
6.
上海外高桥船舶与海洋工程设计研究院, 上海 201306

基金项目:

国家自然科学基金青年科学基金项目 11402143

上海市高校青年教师培养计划项目 A1-2035-14-0010-18

大洋渔业资源可持续开发教育部重点实验室开放基金项目 A1-0203-16-2007-5

国家远洋渔业工程技术研究中心开放基金项目 A1-0203-00-2007-8

详细信息

作者简介:
初文华(1986-), 博士, 讲师, whchu@shou.edu.cn

中图分类号: O383
计量
- 文章访问数: 5444
- HTML全文浏览量: 2077
- PDF下载量: 218
- 被引次数: 0
出版历程
- 收稿日期: 2016-09-18
- 修回日期: 2017-09-06
- 刊出日期: 2018-07-25

Dynamic characteristics of three-dimensional complex structure based on coupling algorithm

CHU Wenhua^{1, 2, 3
,},
ZHU Dongjun⁴,
LIANG Deli⁵,
FENG Feng⁶,
WEI Sijun⁴

1.
College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China
2.
National Engineering Research Center for Oceanic Fisheries, Shanghai 201306, China
3.
Laboratory of Sustainable Exploitation of Oceanic Fisheries Resources, Ministry of Education, Shanghai 201306, China
4.
TRW Automotive Research & Development Shanghai Co. Ltd., Shanghai 200233, China
5.
Science and Technology on Space Physics Laboratory, Beijing 100076, China
6.
Shanghai Waigaoqiao Shipbuilding & Offshore Co. Ltd., Shanghai 201306, China

摘要

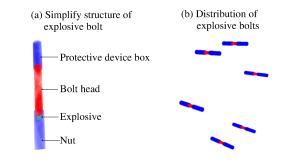
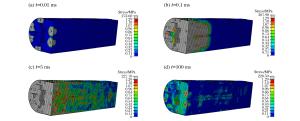
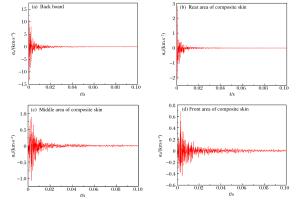
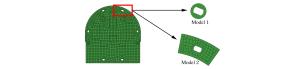
摘要: 光滑粒子流体动力学-有限元耦合算法（SPH-FEM）较好地结合了SPH和FEM的优势，近年来逐渐被引入冲击动力学相关问题研究中。然而早期的研究对象多为单一材料的简单结构，所取得的研究成果距离实际工程应用仍有一定差距。为此，在总结前人工作的基础上，对SPH-FEM耦合算法进行适当改进，通过引入复合材料损伤模型，对复合材料蒙皮结构飞行器舱段结构进行建模计算，分析其在爆炸冲击激励下的冲击动力学特性。将数值计算结果与试验结果进行对比分析，验证该算法和模型的有效性和准确性，初步实现SPH-FEM的工程实际应用。最后总结了复合材料蒙皮结构飞行器在爆炸冲击激励下的一系列结构动态响应规律，以期为航天飞行器结构设计与防护提供参考。
- 耦合算法 /
- 复合材料 /
- 复杂结构 /
- 动力学特性
Abstract: The coupled smoothed particle hydrodynamics-finite element method (SPH-FEM) has been gradually introduced in some researches about the impact dynamics due to its combined advantages of the two algorithms, but the early research focused mostly on simple structures of single material and the results obtained were not applicable in actual engineering. Based on the work previously done, we developed a coupled SPH-FEM method using a damage model of the composite, built a three-dimensional numerical model for the composite skin aircraft structure and studied its impact dynamic characteristics under explosion loading. The comparison of the numerical with experimental results verified the model and algorithm both as valid and accurate, thereby realizing the actual engineering application of the coupled SPH-FEM method. Furthermore, we also analyzed and summarized the dynamic response mechanism of the composite skin aircraft structure under shock loading. Our study can serve as references for the structural design and protection of the aerospace craft.
- coupling algorithm /
- composite material /
- complex structure /
- dynamic characteristics

HTML全文

图 1 复合链表搜索原理

Figure 1. Search principle of compound linked list

下载: 全尺寸图片幻灯片

图 2 复合材料蒙皮结构飞行器数值模型

Figure 2. Numerical model of composite skin aircraft structure

下载: 全尺寸图片幻灯片

图 3 爆炸螺栓三维SPH模型

Figure 3. Three-dimensional SPH model of explosive bolt

下载: 全尺寸图片幻灯片

图 4 第Ⅱ象限内螺栓孔附近区域测点的无量纲化冲击响应谱

Figure 4. Dimensionless shock response spectra of measuring point in quadrant Ⅱ

下载: 全尺寸图片幻灯片

图 5 第Ⅳ象限内螺栓孔附近区域测点的无量纲化冲击响应谱

Figure 5. Dimensionless shock response spectra of measuring point in quadrant Ⅳ

下载: 全尺寸图片幻灯片

图 6 螺栓爆炸分离过程中的冲击压力分布

Figure 6. Pressure profiles in explosion process of explosive bolt

下载: 全尺寸图片幻灯片

图 7 复合材料蒙皮结构飞行器的应力分布

Figure 7. Stress distribution of composite skin aircraft structure

下载: 全尺寸图片幻灯片

图 8 分离结构实现爆炸分离

Figure 8. Explosive separation of separated structure

下载: 全尺寸图片幻灯片

图 9 飞行器结构典型区域冲击加速度时程曲线

Figure 9. Acceleration time histories of typical areas for aircraft structure

下载: 全尺寸图片幻灯片

图 10 分离结构

Figure 10. Separation structure

下载: 全尺寸图片幻灯片

表 1 复合材料层合板材料参数

Table 1. Material parameters of composite laminate

ρ/(g·cm^-3)	E₁₁/GPa	E₂₂/GPa	G₁₂/GPa	ν₁₂	G_f^t/(kN·m^-1)	G_f^c/(kN·m^-1)
1.472	146.8	11.4	6.1	0.30	89.83	78.27

Y_t/MPa	Y_c/MPa	S₁₂/MPa	X_t/MPa	X_c/MPa	G_m^t/(kN·m^-1)	G_m^c/(kN·m^-1)
66.5	268.2	58.7	1730.0	1379.0	0.23	0.76

下载: 导出CSV

表 2 无量纲化冲击响应谱峰值对比

Table 2. Comparison of dimensionless shock response spectrum peak

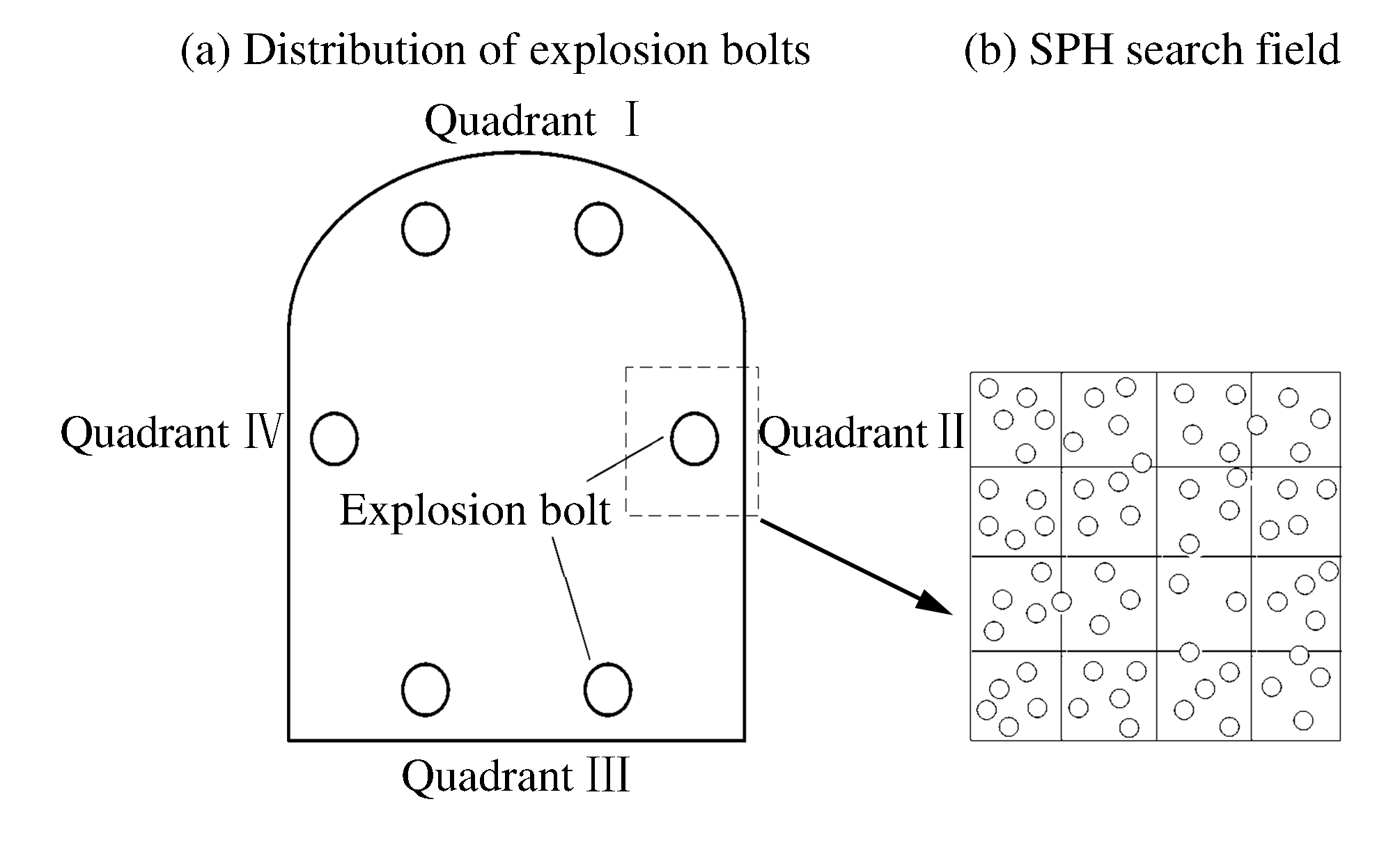
象限	方向	无量纲化冲击响应谱峰值
象限	方向	试验值	计算值	相对误差/%
Ⅱ	轴向径向	0.082 0.115	0.098 0.142	19.51 23.49
Ⅳ	轴向径向	0.174 0.127	0.199 0.144	14.37 13.38

下载: 导出CSV

参考文献(17)

[1]	LIU G R, LIU M B. Smoothed particle hydrodynamics: A meshfree particle method[M]. World Scientific, 2003.
[2]	MING F R, ZHANG A M, XUE Y Z, et al. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions[J]. Ocean Engineering, 2016, 117:359-382. doi: 10.1016/j.oceaneng.2016.03.040
[3]	杨刚, 傅奕轲, 郑建民, 等.基于SPH方法对不同药型罩线性聚能射流形成及后效侵彻过程的模拟[J].振动与冲击, 2016, 35(4):56-61. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zdycj201604010 YANG Gang, FU Yike, ZHENG Jianmin, et al. Simulation of formation and subsequent penetration process of linear shaped charge jets with different liners based on SPH method[J]. Journal of Vibration and Shock, 2016, 35(4):56-61. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zdycj201604010
[4]	刘天生, 张晋红, 李长顺.三种算法在侵彻模拟中的对比研究[J].弹箭与制导学报, 2009, 29(3):117-119. http://www.cqvip.com/QK/97591A/200903/30826989.html LIU Tiansheng, ZHANG Jinhong, LI Changshun. Study on comparison of three algorithms in penetration simulation[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(3):117-119. http://www.cqvip.com/QK/97591A/200903/30826989.html
[5]	JOHNSON G R, STRYK R A, BEISSEL S R, et al. An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation[J]. International Journal of Impact Engineering, 2002, 27(10):997-1013. doi: 10.1016/S0734-743X(02)00030-1
[6]	ATTAWAY S W, HEINSTEIN M W, SWEGLE J W. Coupling of smooth particle hydrodynamics with the finite element method[J]. Nuclear Engineering and Design, 1994, 150(2/3):199-205. https://www.sciencedirect.com/science/article/pii/0029549394901368
[7]	王吉, 王肖钧, 卞梁.光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用[J].爆炸与冲击, 2007, 27(6):522-528. doi: 10.11883/1001-1455(2007)06-0522-07 WANG Ji, WANG Xiaojun, BIAN Liang. Linking of smoothed particle hydrodynamics method to standard finite element method and its application in impact dynamics[J]. Explosion and Shock Waves, 2007, 27(6):522-528. doi: 10.11883/1001-1455(2007)06-0522-07
[8]	卞梁, 王肖钧, 章杰.SPH/FEM耦合算法在陶瓷复合靶抗侵彻数值模拟中的应用[J].高压物理学报, 2010, 24(3):161-167. doi: 10.11858/gywlxb.2010.03.001 BIAN Liang, WANG Xiaojun, ZHANG Jie. Numerical simulations of anti-penetration of confined ceramic targets by SPH/FEM coupling method[J]. Chinese Journal of High Pressure Physics, 2010, 24(3):161-167. doi: 10.11858/gywlxb.2010.03.001
[9]	初文华, 张阿漫, 明付仁, 等.SPH-FEM耦合算法在爆炸螺栓解锁分离过程中的应用[J].振动与冲击, 2012, 31(23):197-202. doi: 10.3969/j.issn.1000-3835.2012.23.036 CHU Wenhua, ZHANG Aman, MING Furen, et al. Application of three-dimensional SPH-FEM coupling method in unlocking process of an explosion bolt[J]. Journal of Vibration and Shock, 2012, 31(23):197-202. doi: 10.3969/j.issn.1000-3835.2012.23.036
[10]	朱东俊, 初文华, 梁德利, 等.基于SPH-FEM耦合算法的飞行器爆炸分离特性研究[J].振动与冲击, 2015, 34(11):68-74. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdycj201511013 ZHU Dongjun, CHU Wenhua, LIANG Deli, et al. Characteristics of a vehicle's pyroshock based on SPH-FEM coupled method[J]. Journal of Vibration and Shock, 2015, 34(11):68-74. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdycj201511013
[11]	张志春, 强洪夫, 高巍然.一种新型SPH-FEM耦合算法及其在冲击动力学问题中的应用[J].爆炸与冲击, 2011, 31(3):243-249. http://www.bzycj.cn/CN/abstract/abstract8663.shtml ZHANG Zhichun, QIANG Hongfu, GAO Weiran. A new coupled SPH-FEM algorithm andits application to impact dynamics[J]. Explosion and Shock Waves, 2011, 31(3):243-249. http://www.bzycj.cn/CN/abstract/abstract8663.shtml
[12]	姜忠涛, 王雷, 孙鹏楠, 等.基于SPH-FEM方法的水下近场爆炸数值模拟研究[J].振动与冲击, 2016, 35(2):129-135. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdycj201602021 JIANG Zhongtao, WANG Lei, SUN Pengnan, et al. Numerical investigation on near-field underwater explosion using SPH-FEM method[J]. Journal of Vibration and Shock, 2016, 35(2):129-135. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_zdycj201602021
[13]	MULVILLE D R. Pyroshock test criteria, NASA technical standard: NASA-STD-7003[R]. Washington D C: National Aeronautics and Space Administration, 1999. http://ci.nii.ac.jp/naid/10008210782
[14]	ZHANG X. Impact damage in composite aircraft structures-experimental testing and numerical simulation[J]. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 1998, 212(4):245-259. doi: 10.1243/0954410981532414
[15]	DOBYNS A L, AVERY J G. Response of advanced composite structures to high explosive blast[C]//Proceedings of the Army Symposium on Solid Mechanics, 1980: 187-203.
[16]	张少实, 庄茁.复合材料与粘弹性力学[M].北京:机械工业出版社, 2005.
[17]	HASHIN Z. Failure criteria for unidirectional fiber composites[J]. Journal of Applied Mechanics, 1980, 47(2):329-334. doi: 10.1115/1.3153664