Oblique penetration on CFRPs by steel sphere
-
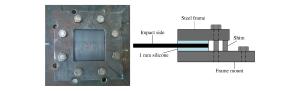
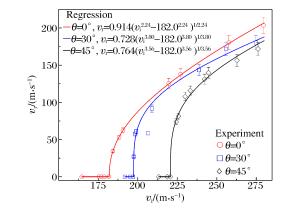
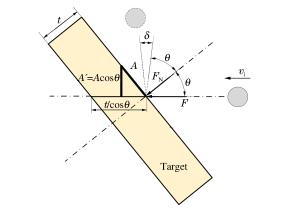
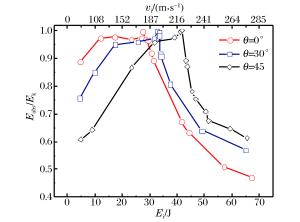
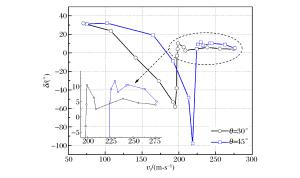
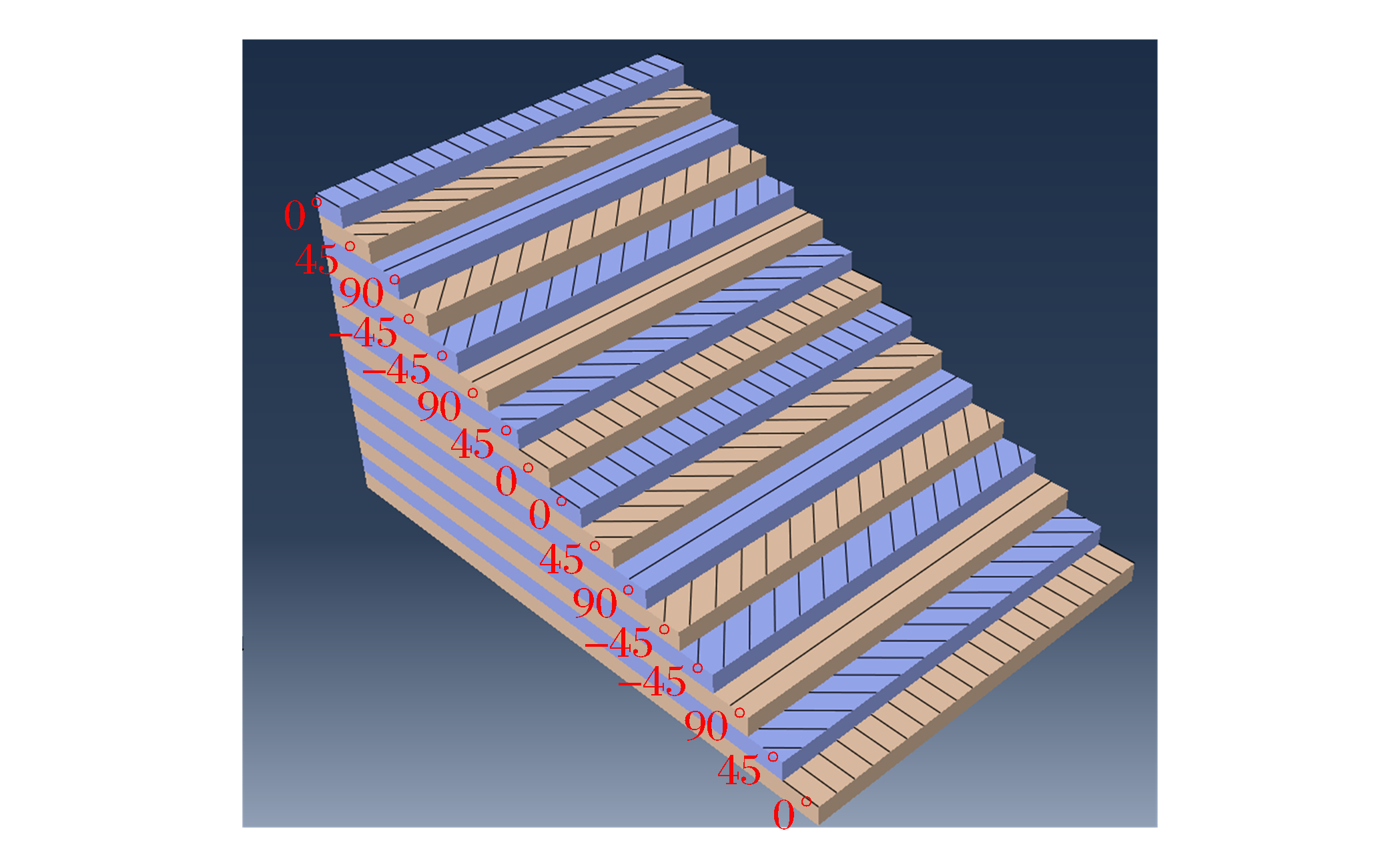
摘要: 为了研究碳纤维复合材料板（CFRPs）在斜侵彻下的抗弹性能，利用一级轻气炮对碳纤维复合材料板进行了70~280 m/s速度范围的0°、30°和45°的侵彻贯穿实验，通过高速摄影技术测量了弹体速度和弹道轨迹。分析了冲击角度对弹道极限、能量吸收和弹道偏转的影响。结果表明：在冲击能量较低时，靶板在正冲击下的能量吸收率比斜冲击高，而当冲击能量较高时则恰好相反；此外，由于弹体穿过层合板的穿透长度随着冲击角度的增加而增加，弹道极限随着冲击角度的增加而增加；而冲击角度对弹道偏转的影响则随着冲击速度的变化而变化。Abstract: In this study we performed a series of penetration tests on specimens of carbon fiber reinforced plastics (CFRPs) using a one-stage gas gun at impact angles of 0°, 30° and 45° at speeds ranging from 70 to 280 m/s to investigate their ballistic resistance behavior in oblique penetration. High speed photography was employed to measure the projectile velocity and ballistic trajectory, and analyzed the influence of the impact angle on their energy absorption, ballistic limit and projectile obliquity variations. The results show that the energy absorption coefficient of the normal impact outperformed the oblique impact at lower impact-energies whereas at the higher impact-energies the ballistic performance was observed to be approximately just the opposite. In addition, due to the increase of the penetration length through the laminate with the impact angle, the ballistic limit increases with the impact angle; the influence of the impact angle on the projectile obliquity varies generally with the impact velocity.
-
图 7 冲击速度约为260 m/s的不同靶板的冲击过程
Figure 7. Impact process of different targets at a velocity around 260 m/s
图 8 斜冲击下的弹体偏转角与冲击速度的关系
Figure 8. Variations in projectile obliquity vs. impact velocity for oblique impacts
表 1 实验结果
Table 1. Experimental results
No. vi/(m·s-1) vr/(m·s-1) vi/(m·s-1) vr/(m·s-1) vi/(m·s-1) vr/(m·s-1) θ=0° θ=30° θ=45° 1 71.7 -23.9 70.3 -34.7 74.8 -46.8 2 118.5 -19.4 107.4 -41.6 102.6 -61.4 3 141.8 -21.4 141.6 -31.5 165.2 -60.4 4 164.6 -28.7 172.2 -34.9 192.3 -39.8 5 175.6 -41.8 191.9 -32.4 213.3 -34.7 6 177.2 -28.4 195.2 -10.6 218.7 -16.2 7 178.9 -10.2 197.0 -16.4 220.7 0 8 181.8 -31.3 197.5 27.0 224.4 74.0 9 184.3 34.5 198.4 57.7 225.8 81.2 10 188.2 53.2 199.0 60.8 230.0 107.8 11 190.7 62.5 206.6 58.5 233.3 115.9 12 219.6 125.5 209.0 91.7 242.3 131.1 13 227.1 137.8 238.8 143.3 244.8 139.8 14 257.7 180.4 255.8 171.9 262.8 156.5 15 279.6 203.4 274.8 180.2 276.1 171.8 
下载: 导出CSV
-
[1] TANG Z, HANG C, SUO T, et al. Numerical and experimental investigation on hail impact on composite panels[J]. International Journal of Impact Engineering, 2017, 105:102-108. doi: 10.1016/j.ijimpeng.2016.05.016 [2] PERNAS-SANCHEZ J, ARTERO-GUERRERO J A, VARAS D, et al. Experimental analysis of ice sphere impacts on unidirectional carbon/epoxy laminates[J]. International Journal of Impact Engineering, 2016, 96:1-10. doi: 10.1016/j.ijimpeng.2016.05.010 [3] DONADON M V, ARBELO M A. Bird strike modeling in fiber-reinforced polymer composites[J]. International Journal of Structural Stability and Dynamics, 2017, 17(6):1750065. doi: 10.1142/S0219455417500651 [4] 秦建兵, 韩志军, 刘云雁, 等.复合材料层合板侵彻行为的研究[J].振动与冲击, 2013, 32(24):122-126. doi: 10.3969/j.issn.1000-3835.2013.24.021QIN Jianbing, HAN Zhijun, LIU Yunyan, et al.Penetration behavior of composite laminated plates[J]. Journal of Vibration and Shock, 2013, 32(24):122-126. doi: 10.3969/j.issn.1000-3835.2013.24.021 [5] 彭刚, 王绪财, 刘原栋, 等.复合材料层板的抗贯穿机理与模拟研究[J].爆炸与冲击, 2012, 32(4):337-345. doi: 10.11883/1001-1455(2012)04-0337-09PENG Gang, WANG Xucai, LIU Yuandong, et al. Research on anti-perforation mechanism and simulation of composite laminates[J]. Explosion and Shock Waves, 2012, 32(4):337-345. doi: 10.11883/1001-1455(2012)04-0337-09 [6] IVAÑEZ I, MOURE M M, GARCIA-CASTILLO S K, et al. The oblique impact response of composite sandwich plates[J]. Composite Structures, 2015, 133:1127-1136. doi: 10.1016/j.compstruct.2015.08.035 [7] CHU C K, CHEN Y L, HSEU G C, et al. The study of obliquity on the ballistic performance of basket fabric composite materials[J]. Journal of Composite Materials, 2007, 41(13):1539-1558. doi: 10.1177/0021998306068098 [8] ASSAF Z, RAN E, BLASS T, et al. Oblique penetration of AP projectile to laminated composites-modeling and verification[C]//The 27th International Symposium on Ballistics. 2012: 1187-1194. [9] POWELL D, ZOHDI T, JOHNSON G. Impact and delamination failure characterization of BSM 8-212 composite aircraft material: DOT/FAA/AR-2008/48[R]//Air Traffic Organization Operations Planning Office of Aviation Research and Development, 2008. https://trid.trb.org/view.aspx?id=879184. [10] LÓPEZ-PUENTE J, ZAERA R, NAVARRO C. An analytical model for high velocity impacts on thin CFRPs woven laminated plates[J]. International Journal of Solids & Structures, 2007, 44(9):2837-2851. https://www.sciencedirect.com/science/article/pii/S0020768306003295 [11] RAJAGOPAL A, NAIK N K. Oblique ballistic impact behavior of composites[J]. International Journal of Damage Mechanics, 2014, 23(4):453-482. doi: 10.1177/1056789513499268 [12] PERNAS-SÁNCHEZ J, ARTERO-GUERRERO J A, VARAS D, et al. Experimental analysis of normal and oblique high velocity impacts on carbon/epoxy tape laminates[J]. Composites Part A:Applied Science & Manufacturing, 2014, 60(3):24-31. https://www.sciencedirect.com/science/article/pii/S1359835X14000207 -
图(8) / 表(1)
计量
- 文章访问数: 5765
- HTML全文浏览量: 1945
- PDF下载量: 230
- 被引次数: 0