Modified method for scaling law based on Cowper-Symonds equation
-
摘要: 针对应变率敏感材料冲击实验的指导需求，给出了一种传统相似理论的修正方法。该方法在已有的动态相似理论基础上，考虑了因实验时模型与全尺寸原型制造材料不同，而导致外载条件相似系数对应变率效应对结果造成的影响：通过引入Cowper-Symonds方程，重新推导了外载条件相似系数的计算公式，并对两种不同材料（是否应变率敏感）的缩放模型冲击实验结果进行讨论，表明该方法相较于传统理论能够准确给出外载条件相似系数、提高模型预测精度。
-
关键词:
- 相似理论 /
- Cowper-Symonds方程 /
- 相似系数 /
- 冲击实验
Abstract: In this paper we proposed a method for modifying classical similarity theories to meet the guidance need in the impact experiment of strain rate sensitive materials. This method, based on recent dynamic similarity theories, took into account the effect of the initial load's similarity coefficients on the strain-rate effect during the impact experiment due to the differences in materials between the prototype and the model. We rebuilt the calculation formulas of the initial load's similarity coefficients using the Cowper-Symonds equation, and discussed the results obtained in the impact experiment on two scaled models, made from two different materials, as to whether they were strain-rate sensitive or not, showing that, compared with the classical similarity theories, our newly proposed method could provide the initial load's accurate similarity coefficients and thus improve the model prediction precision.-
Key words:
- similarity theory /
- Cowper-Symonds equation /
- similarity coefficient /
- impact experiment
-
图 2 4种理论模型与全尺寸原型位移-时间曲线对比
Figure 2. Scaled displacement vs. scaled time as compared between four theoretical models and the prototype
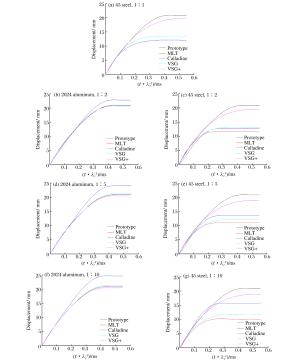
表 1 4种相似理论质量相似系数与速度相似系数
Table 1. Four theories' mass factors & velocity factors
相似系数 λm λυ MLT λ3 1 Calladine λ λ VSG λ3 λq/(q-2)λσ01/(2-q) VSG+ λρλ3 $\sqrt {\frac{{{\lambda _{{\sigma _0}}}}}{{{\lambda _\rho }}}\frac{{{{[1 + {\lambda _v}{{\dot \varepsilon }_{\rm{p}}}/(\lambda {C_{\rm{m}}})]}^1}^{/{p_{\rm{m}}}}}}{{{{(1 + {{\dot \varepsilon }_{\rm{p}}}/{C_{\rm{p}}})}^{1/{p_{\rm{p}}}}}}}} $ 
下载: 导出CSV
表 2 材料参数
Table 2. Parameters of the materials
材料 密度/(g·cm-3) 杨氏模量/GPa 屈服应力/GPa C/s-1 p 2024铝合金 2.73 70 245 1.28×106 4 45钢 7.85 206 420 40 5
下载: 导出CSV
表 3 不同材料及比例尺模型的初始外载条件
Table 3. Initial conditions for models in different materials & scales
材料 比例尺 λm λv MLT Calladine VSG VSG+ MLT Calladine VSG VSG+ 2024铝合金 1:1 1 1 1 1 1 1 1 1 45钢 1:1 1 1 1 2.88 1 1 1.31 0.82 2024铝合金 1:2 0.125 0.5 0.125 0.125 1 0.5 1.00 1.00 45钢 1:2 0.125 0.5 0.125 0.36 1 0.5 1.31 0.85 2024铝合金 1:5 0.008 0.2 0.008 0.008 1 0.2 1.01 1.00 45钢 1:5 0.008 0.2 0.008 0.023 1 0.2 1.32 0.92 2024铝合金 1:10 0.001 0.1 0.001 0.001 1 0.1 1.01 1.00 45钢 1:10 0.001 0.1 0.001 0.00288 1 0.1 1.32 0.98
下载: 导出CSV
-
[1] 沈雁鸣, 陈坚强.超高速碰撞相似律的数值模拟验证[J].爆炸与冲击, 2011, 21(4):343-348. http://www.bzycj.cn/CN/abstract/abstract8681.shtmlSHEN Yanming, CHEN Jianqiang. Numerically simulating verification of the comparability rule on hypervelocity impact[J]. Explosion and Shock Waves, 2011, 21(4):343-348. http://www.bzycj.cn/CN/abstract/abstract8681.shtml [2] BAKER W E, WESTINE P S, DODGE F T. Similarity methods in engineering dynamics:theory and practice of scale modeling[M]. Amsterdam:Elsevier Science Publishers, 1991. [3] 谈庆明. 高速冲击模型律[M]//王礼立. 冲击动力学进展. 合肥: 中国科学技术大学出版社, 1992: 303-320. [4] 谈庆明.量纲分析[M].合肥:中国科学技术大学出版社, 2005. [5] CALLADINE R C. An investigation of impact scaling theory[M]. London:Structural Crashworthiness, Butterworths & Co Publishers, 1983:169-174. [6] OSHIRO R, ALVES M. Scaling of structures subject to impact loads when using a power law constitutive equation[J]. International Journal of Solids Structure, 2009, 46(18/19):3412-3421. https://www.sciencedirect.com/science/article/pii/S0020768309002212 [7] LEMAITRE J, CHABOCHE J L. Mechanics of solids materials[M]. Paris:Dunod, 1988. [8] JONES N. Structural impact[M]. New York:Cambridge University Press, 1997. [9] CHEN Liebin, YANG Jialing. Analytical evaluation of permanent deflection of a thin circular plate struck normally at its center by a projectile[J]. Acta Mechanica Solida Sinica, 2007, 20(2):117-122. doi: 10.1007/s10338-007-0714-0 -
点击查看大图
计量
- 文章访问数: 5532
- HTML全文浏览量: 1521
- PDF下载量: 219
- 被引次数: 0