Shock wave property on interface of wedge explosive and LiF window
-
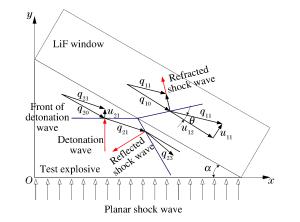
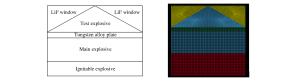
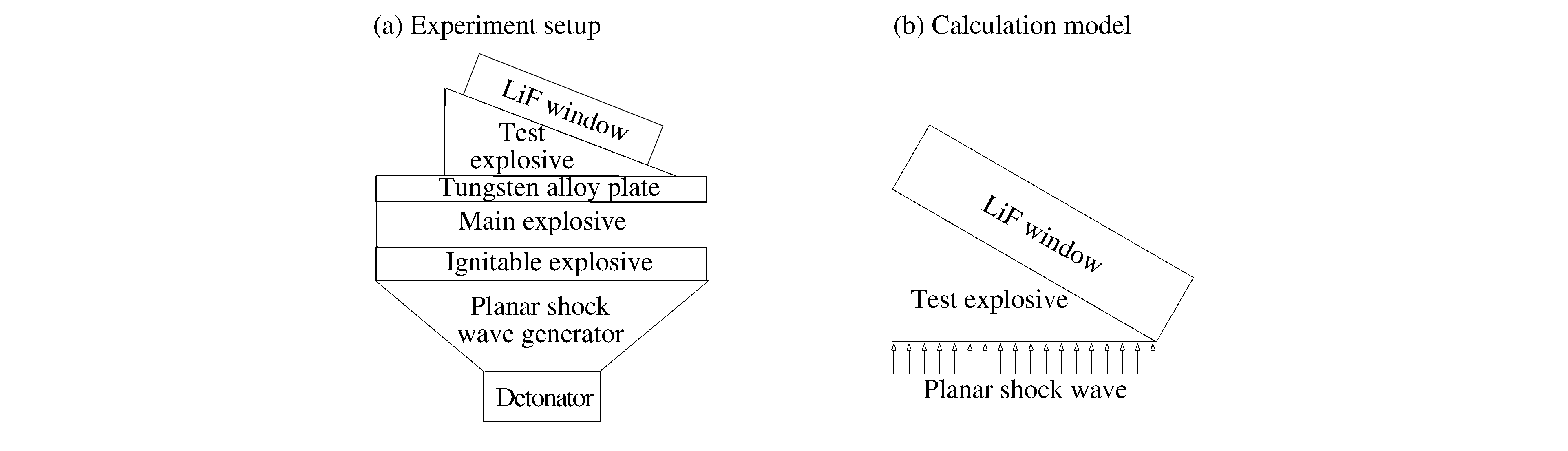
摘要: 采用二维不定常流理论中的极曲线方法，对冲击波进入楔形受试炸药/LiF窗口界面的冲击波波后流场状态进行理论分析，同时采用流体动力学软件LS-DYNA对模型的波后流场状态进行数值模拟。结果表明，对于所研究的模型，一维平面正冲击波进入楔形受试炸药/LiF窗口界面时，由于斜激波的存在，波后粒子运动方向发生偏转，偏转角为3.3°。数值模拟结果表明，在相同模型条件下，冲击波波后粒子偏转角在2.77°~3.03°之间。二者的差异源于极曲线理论中未考虑稀疏波的影响。Abstract: In this study we investigated the property of the shock wave propagating into the LiF window using the pole-curve method of two-dimensional unsteady flow theory and the hydrokinetical software LS-DYNA. The result derived from the pole-curve method shows that, when the one dimensional planar shock wave moves from the wedge-shaped explosive to the LiF window, the moving direction of the particles changes with the angle of about 3.3°, whereas the change angle actually obtained by the LS-DYNA simulation is 2.77°~3.03°. This disparity may be due to the fact that the rarefaction wave is ignored in the pole-curve method.
-
Key words:
- LiF window /
- inclined shock wave /
- pole-curve method /
- wedge-shaped explosive
-
图 2 冲击波前后炸药和LiF中的速度矢量
Figure 2. Velocity vector before and after shock in explosives and LiF
图 4 楔形炸药/LiF窗口界面中不同位置波后粒子速度的垂直分量和水平分量
Figure 4. Particle velocity in vertical and horizontal direction after shock in the interface of wedge-shaped explosive and LiF window
图 5 楔形炸药/LiF窗口界面中波后粒子速度示意
Figure 5. Particle velocity in the interface of wedge-shaped explosive and LiF window
表 1 JO-9159和JBO-9021炸药爆轰产物状态方程参数
Table 1. EOS parameters of detonation products of JO-9159 and JBO-9021
炸药 A/GPa B/GPa R1 R2 ω E/(GJ·m-3) V0 JO-9159 880.7 18.36 4.62 1.32 0.38 10.40 0.543 JBO-9021 613.0 18.58 1.09 4.32 1.79 0.21 0.1 
下载: 导出CSV
表 2 JBO-9021的点火增长模型参数
Table 2. Parameters of ignition and growth model for JBO-9021
I/s-1 ac b x G1/(Pa-1·s-1) c 4×1012 0.02 0.667 7.0 0.09 0.667 d y e f G2/(Pa-3·s-1) z 0.11 1 0.333 1.0 3×10-26 3.0
下载: 导出CSV
表 3 JBO-9021未反应炸药状态方程参数
Table 3. EOS parameters of unreacted JBO-9021
A/TPa B/GPa R1 R2 ω E0/(GJ·m-3) V0 77.810 -5.031 11.3 1.13 0.884 24.9 0.543
下载: 导出CSV
表 4 钨合金和LiF的状态方程参数
Table 4. EOS parameters of tungsten alloy and LiF
材料 ρ0/(g·cm-3) C/(km·s-1) E0/(GJ·m-3) S1 S2 S3 γ0 a 钨合金 19.20 4.028 0 1.243 0 0 1.54 0 LiF 2.64 5.148 0 1.358 0 0 1.69 0
下载: 导出CSV
表 5 LiF窗口中不同位置的波后流场信息
Table 5. Flow field at different positions after shock wave in LiF window
探针 uv/(km·s-1) uh/(km·s-1) u/(km·s-1) θ′/(°) 1 2.03 0.107 2.033 3.03 2 2.05 0.103 2.053 2.88 3 2.07 0.100 2.072 2.77 4 2.05 0.102 2.053 2.85
下载: 导出CSV
-
[1] VANDERSALL K S, TARVER C M, GARCIA F, et al. Shock initiation experiments on PBX9501 explosive at 150 ℃ for ignition and growth modeling[J]. AIP Conference Proceedings, 2006, 845(1):1127-1130. https://www.researchgate.net/profile/Craig_Tarver/publication/253961662_Shock_Initiation_Experiments_on_PBX9501_Explosive_at_150C_for_Ignition_and_Growth_Modeling/links/0c96053cd54751647b000000.pdf?inViewer=true&pdfJsDownload=true&disableCoverPage=true&origin=publication_detail [2] SEITZ W L, STACY H L, ENGELKE R, et al. Detonation reaction zone structure of PBX9502[C]//Proceedings of the Ninth Symposium (International) on Detonation. Portland, Orgegen, 1989: 113291. [3] 张涛, 谷岩, 赵继波, 等.新型高能钝感炸药JBO-9X在较高冲击压力下冲击起爆过程的实验研究[J].火炸药学报, 2016, 39(1):28-33. http://www.cnki.com.cn/Article/CJFDTOTAL-BGXB201601005.htmZHANG Tao, GU Yan, ZHAO Jibo, et al. Experimental study on shock initiation process of a new insensitive high explosive JBO-9X under high impact pressure[J]. Chinese Journal of Explosives & Propellants, 2016, 39(1):28-33. http://www.cnki.com.cn/Article/CJFDTOTAL-BGXB201601005.htm [4] CAMPBELL A W, DAVIS W C, TRAVIS J R. Shock initiation of detonation in liquid explosives[J]. The Physics of Fluids, 1961, 4(4):498-510. doi: 10.1063/1.1706353 [5] CHIDESTER S K, THOMPSON D G, VANDERSALL K S, et al. Shock initiation experiments on PBX 9501 explosive at pressures below 3 GPa with associated ignition and growth modeling[J]. AIP Conference Proceedings, 2007, 955(1):903-906. https://digital.library.unt.edu/ark:/67531/metadc898062 [6] GUSTAVSEN R L, SHEFFIELD S A, ALCON R R, et al. Embedded electromagnetic gauge measurements and modeling of shock initiation in the TATB based explosives LX-17 and PBX 9502[J]. AIP Conference Proceedings, 2002, 620(1):1019-1022. http://adsabs.harvard.edu/abs/2002AIPC..620.1019G [7] BOUYER V, HEBERT P, DOUCET M, et al. Experimental measurements of the chemical reaction zone of TATB and HMX based explosives[J]. AIP Conference Proceedings, 2012, 1426(1):209-212. http://absimage.aps.org/image/SHOCK11/MWS_SHOCK11-2011-000248.pdf [8] ОРЛЕНКО Л П. 爆炸物理学[M]. 孙承纬, 译. 北京: 科学出版社, 2011: 88. [9] TARVER C M, FORBES J W, GARCIA F, et al. Manganin gauge and reactive flow modeling study of the shock initiation of PBX 9501[J]. AIP Conference Proceedings, 2002, 620(1):1043-1046. https://www.researchgate.net/publication/236561084_Manganin_Gauge_and_Reactive_Flow_Modeling_Study_of_the_Shock_Initiation_of_PBX_9501 [10] 张宝坪, 张庆明, 黄风雷.爆轰物理学[M].北京:兵器工业出版社, 2001. -
计量
- 文章访问数: 5035
- HTML全文浏览量: 1687
- PDF下载量: 292
- 被引次数: 0