考虑环境温、湿度的球形装药爆炸冲击波参数计算模型

聂源; 蒋建伟; 门建兵

doi:10.11883/bzycj-2016-0340

考虑环境温、湿度的球形装药爆炸冲击波参数计算模型

doi: 10.11883/bzycj-2016-0340

北京理工大学爆炸科学与技术国家重点实验室, 北京 100081

基金项目:

国家自然科学基金青年基金项目 11502020

详细信息

作者简介:
聂源(1992-), 男, 博士研究生

通讯作者:
蒋建伟, bitjjw@bit.edu.cn

中图分类号: O382.1
计量
- 文章访问数: 5801
- HTML全文浏览量: 2016
- PDF下载量: 245
- 被引次数: 0
出版历程
- 收稿日期: 2016-11-05
- 修回日期: 2017-03-28
- 刊出日期: 2018-07-25

Calculation models for parameters of spherical charge blasting shock wave considering ambient temperature and humidity

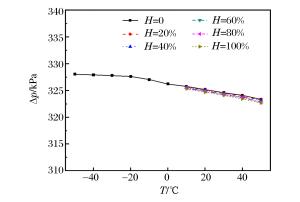
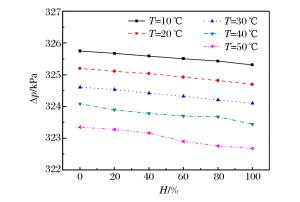
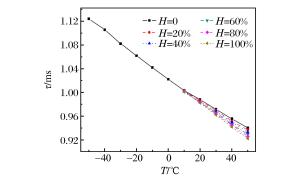
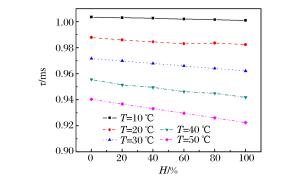
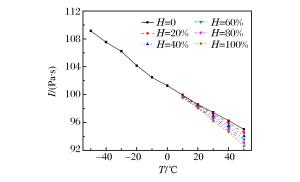
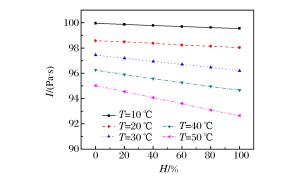
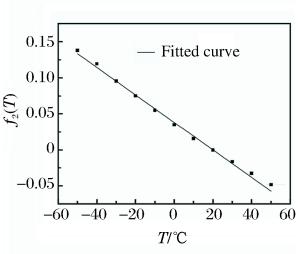
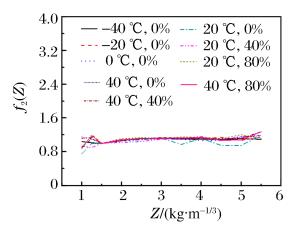
State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 为获得实际温、湿度环境中冲击波参数计算模型，计算了考虑温、湿度的理想气体状态方程参数，利用SPEED软件，针对典型状态空气中球形装药爆炸过程进行数值模拟，得到了温、湿度对爆炸冲击波参数的影响规律。结果表明，温度和相对湿度对冲击波超压的影响较小，而正压作用时间和冲量随温度和相对湿度的升高均呈线性递减关系，在高温高湿和寒冷干燥条件下，冲击波正压作用时间和冲量相差分别达21.8%和18.4%。以经典工程计算模型为基础，通过引入含有温度、湿度和对比距离的修正因子，建立了考虑环境温、湿度的球形装药爆炸冲击波参数的计算模型。采用该模型计算得到的不同药量球形TNT爆炸冲击波参数与数值仿真结果吻合较好，可对装药在实际环境中威力评估提供参考。
- 温度 /
- 相对湿度 /
- 冲击波参数 /
- 计算模型
Abstract: In this study we firstly calculated the parameters of equation of state (EOS) for ideal gas considering temperature and relative humidity to obtain the calculation models for parameters of the blasting shock wave in ambient temperature and humidity. Then, we established the spherical charge model using the SPEED software to simulate the blasting processes in typical air conditions. The results show that the temperature and relative humidity have little influence on the shock wave overpressure, and that both the positive phase duration and the impulse, which are 21.8% and 18.4% smaller in high temperature and humidity than those in the cold and dry air, respectively, decrease linearly with the increase of the temperature and relative humidity. Furthermore, based on classical engineering calculation models, we established the calculation models for the shock wave parameters in spherical charge blasting considering ambient temperature and humidity by introducing correction factors such as temperature, relative humidity and scaled distance. From these models we obtained the blasting shock wave parameters with different doses of spherical TNT. The parameters were found quite consistent with those from numerical simulation, thereby suggesting that the calculation models can serve as reference for power assessment in real environments.
- temperature /
- relative humidity /
- shock wave parameters /
- calculation models

HTML全文

图 1 数值仿真模型

Figure 1. Numerical simulation model

下载: 全尺寸图片幻灯片

图 2 Δp-T曲线

Figure 2. Δp-T curves

下载: 全尺寸图片幻灯片

图 3 Δp-H曲线

Figure 3. Δp-H curves

下载: 全尺寸图片幻灯片

图 4 τ-T曲线

Figure 4. τ-T curves

下载: 全尺寸图片幻灯片

图 5 τ-H曲线

Figure 5. τ-H curves

下载: 全尺寸图片幻灯片

图 6 I-T曲线

Figure 6. I-T curves

下载: 全尺寸图片幻灯片

图 7 I-H曲线

Figure 7. I-H curves

下载: 全尺寸图片幻灯片

图 8 f₂(T)-T曲线

Figure 8. f₂(T)-T curves

下载: 全尺寸图片幻灯片

图 9 f₂(H)-H曲线

Figure 9. f₂(H)-H curves

下载: 全尺寸图片幻灯片

图 10 f₂(Z)-Z曲线

Figure 10. f₂(Z)-Z curves

下载: 全尺寸图片幻灯片

图 11 f₃(T)-T曲线

Figure 11. f₃(T)-T curves

下载: 全尺寸图片幻灯片

图 12 f₃(H)-H曲线

Figure 12. f₃(H)-H curves

下载: 全尺寸图片幻灯片

图 13 f₃(Z)-Z曲线

Figure 13. f₃(Z)-Z curves

下载: 全尺寸图片幻灯片

图 14 计算模型与数值模拟得到的正压作用时间对比

Figure 14. Comparison between numerical simulation and calculation results of τ

下载: 全尺寸图片幻灯片

图 15 计算模型与数值模拟得到的冲量对比

Figure 15. Comparison between numerical simulation and calculation results of I

下载: 全尺寸图片幻灯片

表 1 典型温度和相对湿度的空气参数

Table 1. Parameters of ideal gas equation of state for air at typical temperature and relative humidity

T/℃	H/%	ρ/(kg·m^-3)	γ	c_Vm/(J·kg^-1)	e/(J·g^-1)
-40	0	1.514	1.399266	719.0700	167.6512
-20	0	1.394	1.399266	719.0700	182.0326
0	0	1.292	1.399266	719.0700	196.4140
20	0	1.204	1.399266	719.0700	210.7954
20	100	1.193	1.397167	729.2962	213.7932
40	0	1.127	1.399266	719.0700	225.1768
40	100	1.096	1.392724	751.9399	235.4700

下载: 导出CSV

表 2 TNT炸药JWL状态方程参数^[13]

Table 2. Parameters of JWL equation of state for TNT explosive^[13]

ρ₀/(g·cm^-3)	A/GPa	B/GPa	R₁	R₂	ω	E₀/GPa
1.67	373.8	3.747	4.15	0.90	0.35	6.00

下载: 导出CSV

参考文献(14)

[1]	HENRYCH J, ABRAHAMSON G R. The dynamics of explosion and its use[M]. New York: Elsevier Scientific Publishing, 1979.
[2]	BAKER W E. Explosions in air[M]. Austin: University of Texas Press, 1974:6-10.
[3]	SADOVSKYI M A. Mechanical action of air shock waves of explosion based on experimental data[M]. Moscow: Izd Akad Nauk SSSR, 1952:1-2.
[4]	IZADIFARD R A, FOROUTAN M. Blastwave parameters assessment at different altitude using numerical simulation[J]. Turkish Journal of Engineering & Enviromental Sciences, 2010, 34(1):25-41. https://www.researchgate.net/publication/268327410_Blastwave_parameters_assessment_at_different_altitude_using_numerical_simulation
[5]	顾垒, 向文飞.爆炸空气冲击波超压影响因素分析及控制[J].爆破, 2002, 19(2):15-17. http://cdmd.cnki.com.cn/Article/CDMD-10151-1015359201.htm GU Lei, XIANG Wenfei.Analyses on influential factors about airblast overpressure and its control[J]. Blasting, 2002, 19(2):15-17. http://cdmd.cnki.com.cn/Article/CDMD-10151-1015359201.htm
[6]	王琦, 石全, 史宪铭, 等.基于均匀实验设计的温压战斗部爆炸冲击波毁伤仿真研究[J].军械工程学院学报, 2011, 23(3):31-37. http://cdmd.cnki.com.cn/Article/CDMD-80137-2007135057.htm WANG Qi, SHI Quan, SHI Xianming, et al. Research on damage model of thermo-baric warhead to underground objects based on the uniform design[J].Journal of Ordnance Engneering College, 2011, 23(3):31-37. http://cdmd.cnki.com.cn/Article/CDMD-80137-2007135057.htm
[7]	聂源, 蒋建伟, 李梅.球形装药动态爆炸冲击波超压场计算模型[J].爆炸与冲击, 2017, 37(5):951-956. doi: 10.11883/1001-1455(2017)05-0951-06 NIE Yuan, JIANG Jianwei, LI Mei. Overpressure calculation model of sphere charge blasting with moving velocity[J]. Explosion and Shock Waves, 2017, 37(5):951-956. doi: 10.11883/1001-1455(2017)05-0951-06
[8]	侯俊亮, 蒋建伟, 门建兵, 等.不同形状装药爆炸冲击波场及对靶板作用效应的数值模拟[J].北京理工大学学报, 2013, 33(6):556-561. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjlgdxxb201306002 HOU Junliang, JIANG Jianwei, MEN Jianbing, et al. Numerical simulation on blast wave field and deformation of thin plate under different-shape charge loading[J]. Transactions of Beijing Institute of Technology, 2013, 33(6):556-561. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=bjlgdxxb201306002
[9]	李加贵, 边小华, 张雷.爆炸冲击波传播的数值模拟与试验数据对比[J].山西建筑, 2006, 32(8):106-107. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=shanxjz200608068 LI Jiagui, BIAN Xiaohua, ZHANG Lei. Numerical simulation of blast wave propagation in tunnel compared with experiment data[J]. Shanxi Architecture, 2006, 32(8):106-107. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=shanxjz200608068
[10]	NUMERICS GmbH. SPPED user's manual[M/OL]. 2012[2016-08-07]. http://www.alpha-numerics.de/.
[11]	HOBGOOD J S. Introduction to atmospheric thermodynamics[M]. Cambridge: Cambridge Univercity Press, 2002, 84(47):520-520.
[12]	陈创买, 郭英琼.气象常用参数和物理量查算表[M].北京:气象出版社, 1980.
[13]	LEE E L, FINGER M, COLLINS W. JWL equation of state coeffients for high explosives: UCID-16189[R]. CA: Lawrence Livermore National Laboratory, 1973. https://www.osti.gov/scitech/biblio/4479737
[14]	张社荣, 孔源, 王高辉.水下和空中爆炸冲击波传播特性对比分析[J].振动与冲击, 2014, 33(13):148-153. http://www.cnki.com.cn/Article/CJFDTotal-ZDCJ201413027.htm ZHANG Sherong, KONG Yuan, WANG Gaohui. Comparative analysis on propagation characteristics of shock wave induced by underwater and air explosions[J]. Journal of Vibration and Shock, 2014, 33(13):148-153. http://www.cnki.com.cn/Article/CJFDTotal-ZDCJ201413027.htm