Propagation characteristics and failure behaviors of crack in tunnel under impact loads
-
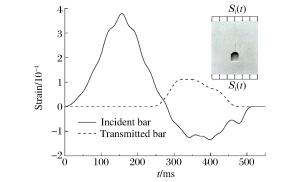
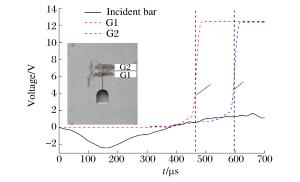
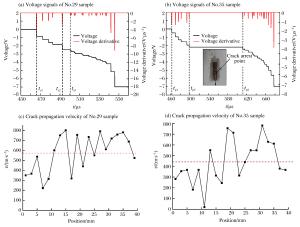
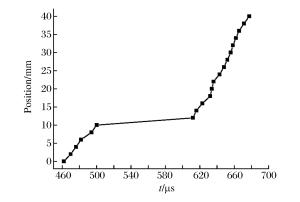
摘要: 为了开展含预制裂纹的巷道模型试样在冲击载荷下的动态断裂响应实验，选用青砂岩作为模型材料制作巷道模型试样，以可调速落锤冲击实验机作为冲击加载装置进行试样的动态断裂实验，分析冲击载荷作用下的巷道内裂纹的扩展规律。采用裂纹扩展计及应变片测试系统监测裂纹的起裂时间、扩展速度及止裂时间，并借助于AUTODYN、ABAQUS有限元数值分析软件对实验模型进行数值模拟，计算裂纹的动态起裂韧度、动态扩展韧度、动态止裂韧度等断裂参数。结果表明：巷道内裂纹在扩展路径过程中存在着明显的止裂现象；采用实验-数值方法能够较好地得出裂纹的起裂韧度、扩展韧度和止裂韧度等参数。另外，对止裂现象进行了初步的分析，讨论了试样内应力反射波与透射波对止裂问题的影响。Abstract: In order to obtain the dynamic response of the pre-cracked tunnel under impact loads, we investigated the crack propagation characteristics in the tunnel using the green sandstone as the model material of the tunnel, and the self-developed adjustable speed-drop hammer impact tester that can realize low- and medium-impact loading speed as the loading device. We determined the crack's initiation time, propagation velocity and arrest time, using a measuring system consisting of a crack propagation gauge and a strain gauge, and successfully obtained the crack's initiation toughness, propagation toughness and arrest toughness using the finite element software AUTODYN and ABAQUS based on the test data. The results showed that crack arrest occurred in the process of crack propagation; and that the experimental-numerical method can be successfully used to calculate the crack initiation toughness, propagation toughness and arrest toughness. Further, we conducted a preliminary analysis of crack arrest, and examined the influence of internal stress reflection wave and transmission wave on crack arrest.
-
Key words:
- tunnel /
- crack /
- initiation toughness /
- propagation toughness /
- arrest toughness /
- propagation velocity
-
图 4 入射杆及透射杆上记录的应变-时间曲线
Figure 4. Curves of strain-time recorded from incident and transmitted bars
图 5 监测点应变片断裂时间确定方式
Figure 5. Method for determining fracture time of the strain gauges
图 6 试样中CPG记录的两种不同电压信号及测试的裂纹扩展速度
Figure 6. Two different voltage signals recorded and the crack propagation velocity by CPG in the tunnel specimen
图 8 数值分析结果与实验破坏结果对比
Figure 8. Comparison between numerical results and experimental results
图 9 裂纹尖端坐标及1/4节点奇异单元
Figure 9. Coordinates and 6 nodes triangular element displacement
表 1 采用实验-数值方法得到的动态断裂韧度
Table 1. Dynamic fracture toughness obtained by experimental-numerical method
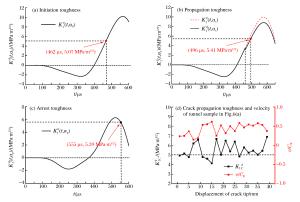
试样编号 tf/μs va/(m·s-1) KⅠCD/(MPa·m1/2) $ \dot{K} $/(kPa·m1/2·s-1) 29 468.2 578.47 5.55 11.85 30 458.4 584.93 6.12 13.35 35 460.8 438.49 4.45 9.66 40 457.2 596.05 6.96 15.22 47 462.0 511.11 5.07 10.97 
下载: 导出CSV
-
[1] 王蒙, 朱哲明, 王雄.冲击荷载作用下的Ⅰ/Ⅱ复合型裂纹扩展规律研究[J].岩石力学与工程学报, 2016, 35(7):1323-1332. http://cdmd.cnki.com.cn/Article/CDMD-10674-1015635867.htmWANG Meng, ZHU Zheming, WANG Xiong. The growth of mixed-mode Ⅰ/Ⅱ under impacting loads[J]. Journal of Rock Mechanics and Engineering, 2016, 35(7):1323-1332. http://cdmd.cnki.com.cn/Article/CDMD-10674-1015635867.htm [2] WANG Q Z, FENG F, NI M, et al. Measurement of mode Ⅰ and mode Ⅱ rock dynamic fracture toughness with cracked straight through flattened Brazilian disc impacted by split Hopkinson pressure bar[J]. Engineering Fracture Mechanics, 2011, 78(12):2455-2469. doi: 10.1016/j.engfracmech.2011.06.004 [3] 李炼, 杨丽萍, 曹富, 等.冲击加载下的砂岩动态断裂全过程的实验和分析[J].煤炭学报, 2016, 41(8):1912-1922. http://industry.wanfangdata.com.cn/jt/Detail/Periodical?id=Periodical_mtxb201608006LI Lian, YANG Liping, CAO Fu, et al. Complete dynamic fracture process of sandstone under impact loading: experiment and analysis[J]. Journal of China Coal Society, 2016, 41(8):1912-1921. http://industry.wanfangdata.com.cn/jt/Detail/Periodical?id=Periodical_mtxb201608006 [4] 杨井瑞, 张财贵, 周妍, 等.用CSTBD试样确定砂岩的动态起裂和扩展韧度[J].爆炸与冲击, 2014, 34(3):264-271. doi: 10.11883/1001-1455(2014)03-0264-08YANG Jingrui, ZHANG Caigui, ZHOU Yan, et al. Determination of dynamic initiation toughness and propagation toughness of sandstone using CSTBD specimens[J]. Explosion and Shock Waves, 2014, 34(3):264-271. doi: 10.11883/1001-1455(2014)03-0264-08 [5] ZHANG Q B, ZHAO J. Effect of loading rate on fracture toughness and failure micromechanisms in marble[J]. Engineering Fracture Mechanics, 2013, 102(2):288-309. https://www.sciencedirect.com/science/article/pii/S0013794413000519 [6] ZHANG Q B, ZHAO J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 60(8):423-439. https://www.researchgate.net/publication/264979473_Determination_of_mechanical_properties_and_full-field_strain_measurements_of_rock_material_under_dynamic_loads [7] 潘峰, 党发宁, 焦凯, 等.冲击荷载作用下不均匀脆性材料动态弯拉强度提高机制研究[J].岩石力学与工程学报, 2015(增刊2):3948-3955. http://www.cnki.com.cn/Article/CJFDTotal-YSLX2015S2039.htmPAN Feng, DANG Faning, JIAO Kai, et al. Mechanism on enhancement of dynamic flexural tensile strength for nonuniform brittle materials under impact loading[J]. Chinese Journal of Rock Mechanics & Engineering, 2015, 2015(Suppl 2):3948-3955. http://www.cnki.com.cn/Article/CJFDTotal-YSLX2015S2039.htm [8] 宋义敏, 何爱军, 王泽军, 等.冲击载荷作用下岩石动态断裂试验研究[J].岩土力学, 2015, 36(4):965-970. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201504009.htmSONG Yiming, HE Aijun, WANG Zejun, et al. Experiment study of the dynamic fractures of rock under impact loading[J]. Rock and Soil Mechanics, 2015, 36(4):965-970. http://www.cnki.com.cn/Article/CJFDTOTAL-YTLX201504009.htm [9] BHAT H S, ROSAKIS A J, SAMMIS C G. A micromechanics based constitutive model for brittle failure at high strain rates[J]. Journal of Applied Mechanics, 2012, 79(3):031016. doi: 10.1115/1.4005897 [10] FREUND L B. Dynamic fracture mechanics[M]. Cambridge: Cambridge University Press, 1998. [11] REN X D, LI J. Dynamic fracture in irregularly structured systems[J]. Physical Review E, 2012, 85(2):988-1000. https://vdocuments.site/documents/dynamic-fracture-in-irregularly-structured-systems.html [12] 张财贵, 曹富, 李炼, 等.采用压缩单裂纹圆孔板确定岩石动态起裂、扩展和止裂韧度[J].力学学报, 2016, 48(3):624-635. doi: 10.6052/0459-1879-15-349ZHANG Caigui, CAO Fu, LI Lian, et al. Determination of dynamicfracture initiation, propagation, and arrest toughness of rock using SCDC specimen[J]. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(3):624-635. doi: 10.6052/0459-1879-15-349 [13] HU R, ZHU Z, XIE J, et al. Numerical study on crack propagation by using softening model under blasting[J]. Advances in Materials Science and Engineering, 2015:1-9. https://www.hindawi.com/journals/amse/2015/108580/ [14] KONOKMAN H E, CORUH M M, KAYRAN A. Computational and experimental study of high-speed impact of metallic Taylor cylinders[J]. Acta mechanica, 2011, 220(1):61-85. doi: 10.1007/s00707-011-0467-1 [15] WU C, HAO H. Numerical prediction of rock mass damage due to accidental explosions in an underground ammunition storage chamber[J]. Shock Waves, 2006, 15(1):43-54. doi: 10.1007/s00193-005-0004-z [16] ZAIDI A M A, KOSLAN F S, OTHMAN Z, et al. Appropriate coupling solvers for the numerical simulation of rolled homogeneous armor plate response subjected to blast loading[J]. Advances in Mechanical Engineering, 2013, 5:637564. doi: 10.1155/2013/637564 [17] ZHU Z M. Numerical prediction of crater blasting and bench blasting[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(6):1088-1096. doi: 10.1016/j.ijrmms.2009.05.009 [18] ZHU Z M, WANG C, KANG J M, et al. Study on the mechanism of zonal disintegration around an excavation[J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 67(4):88-95. https://www.sciencedirect.com/science/article/pii/S136516091400015X [19] ZHU Z M, MOHANTY B, XIE H P. Numerical investigation of blasting-induced crack initiation and propagation in rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3):412-424. doi: 10.1016/j.ijrmms.2006.09.002 [20] ZHU Z M, XIE H P, MOHANTY B. Numerical investigation of blasting-induced damage in cylindrical rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2):111-121. doi: 10.1016/j.ijrmms.2007.04.012 [21] 周磊, 朱哲明, 刘邦.隧道周边不同位置径向裂纹对隧道围岩稳定性影响规律的研究[J].岩土工程学报, 2016, 38(7):1230-1237. http://www.cnki.com.cn/Article/CJFDTotal-YTGC201607009.htmZHOU Lei, ZHU Zheming, LIU Bang. Influence of radial cracks on stability of surrounding rocks at different locations around tunnel[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7):1230-1237. http://www.cnki.com.cn/Article/CJFDTotal-YTGC201607009.htm [22] 李为民, 许金余.大直径分离式霍普金森压杆试验中的波形整形技术研究[J].兵工学报, 2009, 30(3):350-355. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_bgxb200903019LI Weiming, XU Jinyu. Pulse shaping techniques for large-diameter split Hopkinson pressure bar test[J]. Acta Armamentarii, 2009, 30(3):350-355. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_bgxb200903019 [23] JIANG F C, LIU R T, ZHANG X X, et al. Evaluation of dynamic fracture toughness KⅠd by Hopkinson pressure bar loaded instrumented Charpy impact test[J]. Engineering fracture mechanics, 2004, 71(3):279-287. doi: 10.1016/S0013-7944(03)00139-5 [24] HENSCHEL S, KRUGER L. Dynamic crack initiation measurements in a four-point split Hopkinson bending device[J]. Engineering Fracture Mechanics, 2015, 133:62-75. doi: 10.1016/j.engfracmech.2015.05.020 [25] CHEN Y M. Numerical computation of dynamic stress intensity factors by a Lagrangian finite-difference method (the HEMP code)[J]. Engineering Fracture Mechanics, 1975, 7(4):653-660. doi: 10.1016/0013-7944(75)90021-1 [26] 郦正能.应用断裂力学[M].北京:北京航空航天大学出版社, 2012:12-16.LI Zhengneng. Application of fracture mechanics[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 2012:12-16. [27] RAVI-CHANDAR K. Dynamic Fracture[M]. Amsterdam: Elsevier, 2004. [28] ROSE L R F. Recent theoretical and experimental results on fast brittle fracture[J]. International Journal of Fracture, 1976, 12(6):799-813. doi: 10.1007/BF00034620 -
点击查看大图
图(10) / 表(1)
计量
- 文章访问数: 5246
- HTML全文浏览量: 1977
- PDF下载量: 193
- 被引次数: 0