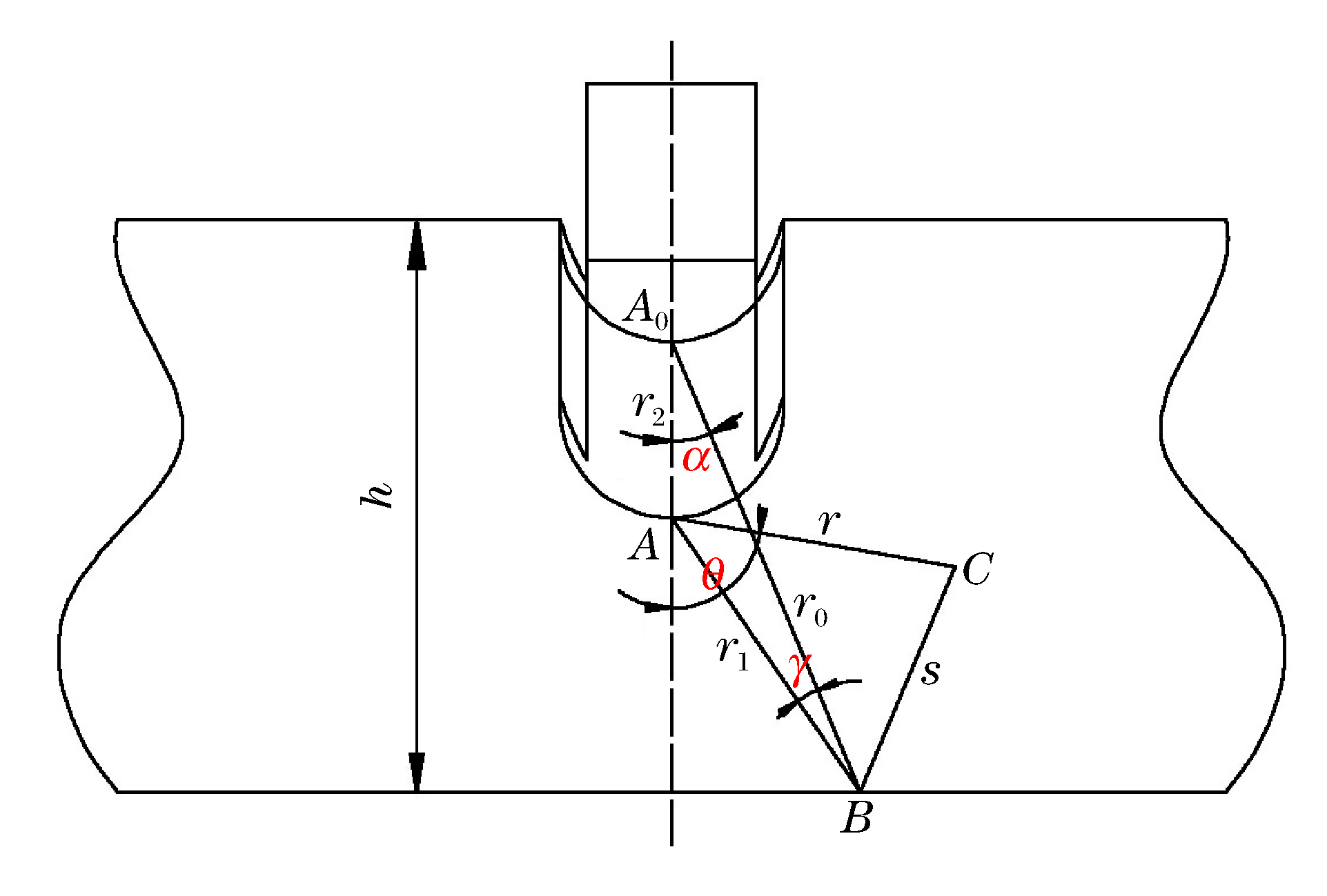
Spallation of targets subjected to vertical penetraion of explosively-formed projectiles
-
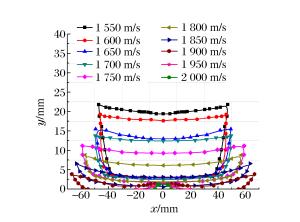
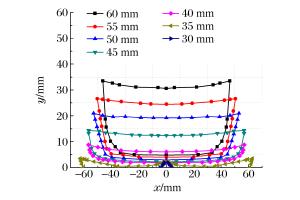
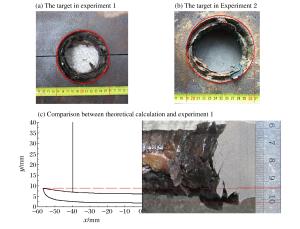
摘要: 为了准确掌握靶板层裂过程和规律，基于波动力学和基本假设，建立了爆炸成型弹丸（explosively formed projectile，EFP）垂直侵彻有限厚靶板时层裂的力学模型，得到了层裂点的表达式。研究结果表明：EFP速度为1 800 m/s、靶板厚度从35 mm增大到60 mm时，靶板背面弯月形层裂区厚度不断增大，弯月形层裂区长度不断减小；靶板厚度保持40 mm不变、EFP速度从1 600 m/s增大到1 900 m/s时，靶板背面层裂区厚度不断减小，弯月形层裂区长度不断增大。开展了EFP侵彻40 mm厚装甲钢靶板的实验，将实验结果和理论计算结果进行对比分析，两者吻合较好。Abstract: In order to understand the spallation of a target subjected to the impact load of an explosively formed projectile (EFP), on the basis of wave mechanics and basic assumptions, a mechanical model was developed to describe the spallation of the finite-thickness target vertically penetrated by an EFP. By the developed model, the spallation process of the target plate was obtained, and its formula was derived. The result shows as following. When the impact velocity of the EFP is 1 800 m/s and the thickness of the target increases from 35 mm to 60 mm, the thickness of the falcate spallation zone at the back of the target increases and its length decreases. When the thickness of the target is 40 mm and the impact velocity increases from 1 600 m/s to 1 900 m/s, the thickness of the falcate spallation zone at the back of the target decreases and its length increases. Dynamic tests were carried out on the EFPs penetration into the rolled homogeneous armor targets with the thickness of 40 mm. The experimental result is in good agreement with the theoretical prediction.
-
Key words:
- explosively-formed projectile /
- vertical penetraion /
- spallation /
- impact load
-
图 1 入射波和反射波相互作用示意图
Figure 1. Schematic diagram of interaction between incident and reflected waves
图 2 不同EFP速度下靶板背面发生层裂的区域
Figure 2. Spallation zones at target backs at different EFP velocities
图 3 不同厚度靶板背面发生层裂的区域
Figure 3. Spallation zones at target backswith different thicknesses
表 1 层裂参数的实验结果和理论计算结果
Table 1. Experimental and theorical results of spallation parameters
层裂厚度/mm 层裂长度/mm 理论计算 实验1 实验2 理论计算 实验1 实验2 8.8 8.4 9.1 114.0 110.8 116.1 
下载: 导出CSV
-
[1] RINEHART J S, PEARSON J. Conical surfaces of fracture produced by asymmetrical impulsive loading[J]. Journal of Applied Physics, 1952, 23(6):685-687. doi: 10.1063/1.1702279 [2] RINEHART J S. Stress transients in solids[M]. Santa Fe, New Mexico:HyperDynamics, 1975:212-215. [3] REN Bo, LI Shaofan, QIAN Jing, et al. Meshfree simulations of spall fracture[J]. Computer Methods in Applied Mechanics and Engineering, 2011, 200(5/6/7/8):797-811. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=JJ0224104199 [4] YU V B, SAVELEVA N V, NAIMARK O B. Numerical simulation of dynamic failure and multi spall fracture in metals[J]. Journal of Physics:Conference Series, 2016, 774(1):012063. http://cn.bing.com/academic/profile?id=f83b063994a23613a1a8bcd0d00584f5&encoded=0&v=paper_preview&mkt=zh-cn [5] 杜忠华.动能弹侵彻陶瓷复合装甲机理[D].南京: 南京理工大学, 2002: 61-64. http://cdmd.cnki.com.cn/Article/CDMD-10288-2003104675.htm [6] 陈大年, 谭华, 俞宇颖, 等.一种基于空穴聚集的层裂模型[J].爆炸与冲击, 2006, 26(2):97-104. doi: 10.3321/j.issn:1001-1455.2006.02.001CHEN Danian, TAN Hua, YU Yuying, et al. A spallation model based on hole coalescence[J]. Explosion and Shock Waves, 2006, 26(2):97-104. doi: 10.3321/j.issn:1001-1455.2006.02.001 [7] 刘飞, 唐献述, 任新见.接触爆炸作用下钢板层裂效应数值分析[J].工程爆破, 2011, 17(2):15-18. doi: 10.3969/j.issn.1006-7051.2011.02.004LIU Fei, TANG Xianshu, REN Xinjian. Numerical analysis of spall effect of steel plate under contact explosion[J]. Engineering Blasting, 2011, 17(2):15-18. doi: 10.3969/j.issn.1006-7051.2011.02.004 [8] 魏波.冲击载荷下材料层裂的数值模拟[D].南京: 南京理工大学, 2013: 20-51. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2275664 [9] 王礼立.应力波基础[M].北京:国防工业出版社, 2005:238-239. [10] ZU X, HUANG Z, XIAO Q, et al. Theoretical study on equivalent target of ceramic composite armor[J]. Propellants, Explosives, Pyrotechnics, 2015, 40(4):576-582. doi: 10.1002/prep.v40.4 [11] HELD M. Verification of the equation for radial crater growth by shaped charge jet penetration[J]. International Journal of Impact Engineering, 1995, 17(1/2/3):387-398. doi: 10.1016-0734-743X(95)99864-N/ [12] NEUBERGER A, PELES S, RITTEL D. Scaling the response of circular plates subjected to large and close-range spherical explosions. Part Ⅰ:Air-blast loading[J]. International Journal of Impact Engineering, 2007, 34(5):859-873 doi: 10.1016/j.ijimpeng.2006.04.001 -
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 5051
- HTML全文浏览量: 2076
- PDF下载量: 148
- 被引次数: 0