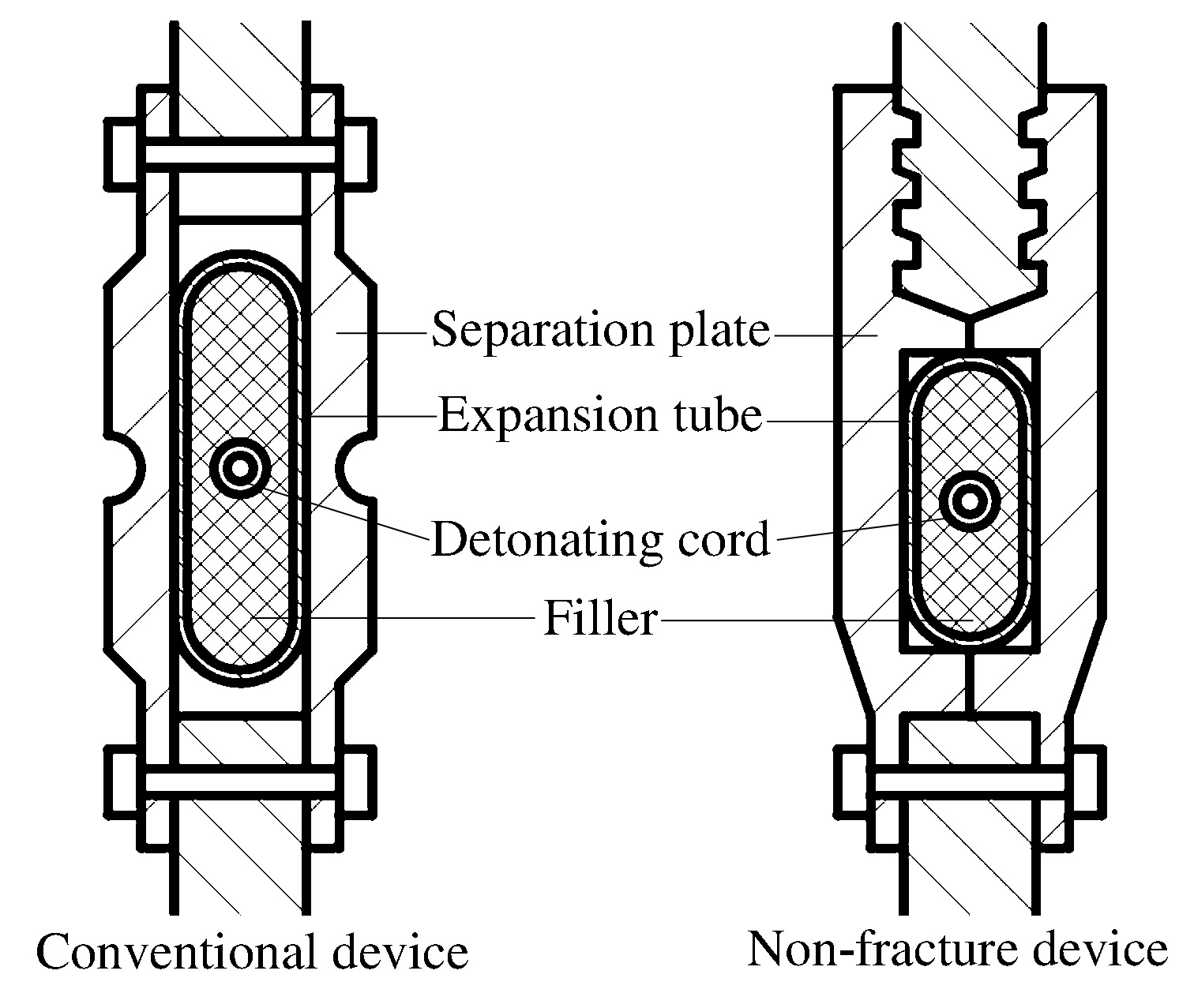
Design and analysis of a non-fracture super-zip separation device
-
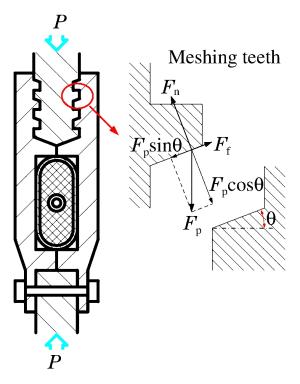
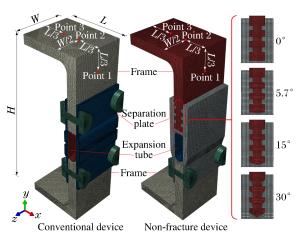
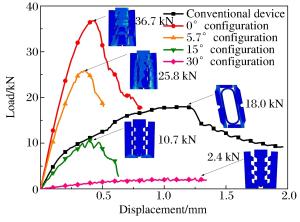
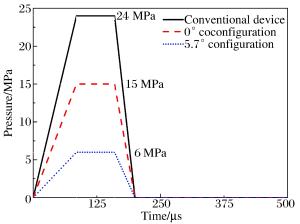
摘要: 对一种新型非断裂式膨胀管分离装置进行了静力承载及分离冲击动响应分析。根据静力承载分析，获得了其啮合齿倾角与承压能力间的关系，结果显示，当接触面摩擦因数恒定时，非断裂式膨胀管分离装置的承压能力与啮合齿倾角大小呈反比，且可靠承压的临界啮合角为啮合齿自锁角。同时，根据动力响应分析，获得了非断裂式膨胀管分离装置在不同啮合齿倾角情况下的分离冲击响应，并与常规膨胀管分离装置的分离冲击响应进行了对比，结果显示，所分析的两种具有不同啮合齿倾角的非断裂式膨胀管分离装置具有比常规膨胀管分离装置更小的可靠分离内压，并且5.7°啮合齿倾角构型在相同测点处的三向加速度时程曲线峰值均低于常规膨胀管分离装置。Abstract: The load-bearing capacity and shock response of a state-of-the-art non-fracture super-zip separation device have been analyzed. Based on the static load-bearing analysis, the relationship between the meshing angle and the load-bearing capacity of the non-fracture super-zip separation device has been obtained. The results show that load-bearing capacity is inversely proportional to the angle of meshing teeth and that the critical meshing angle for reliable load-bearing is the self-locking angle of meshing teeth when the friction coefficient of the contact surfaces is constant. By means of the dynamic response analysis, the separation shock responses of the separation devices with different configurations have been gotten. The results show that the two kinds of non-fracture separation devices with different meshing angle can be separated under lower inner pressure compared with the conventional super-zip separation device, and that the peak values of the acceleration history curves of the non-fracture separation device with 5.7° meshing angle configuration are smaller than those of the conventional super-zip separation device at the same measuring points in all three directions.
-
图 1 常规及非断裂式膨胀管分离装置
Figure 1. Conventional and non-fracture super-zip separation devices
图 2 非断裂式膨胀管分离装置啮合齿受力分析
Figure 2. Force analysis of meshing teeth of non-fracture super-zip separation device under compression
图 3 常规及非断裂式膨胀管分离装置有限元模型
Figure 3. FEM models of conventional and non-fracture super-zip separation devices
图 4 常规及非断裂式膨胀管分离装置承压性能曲线
Figure 4. Load-displacement curves of conventional and non-fracture super-zip separation devices
图 9 各型膨胀管分离装置分离时刻状态
Figure 9. The states of different separation devices at the time of separation
图 10 测点1处x方向的加速度时程曲线
Figure 10. Acceleration histories of x directoin at measuring point 1
图 11 测点1处y方向的加速度时程曲线
Figure 11. Acceleration histories of y directoin at measuring point 1
图 12 测点1处z方向的加速度时程曲线
Figure 12. Acceleration histories of z directoin at measuring point 1
表 1 分离装置各部件材料属性
Table 1. Material parameters of separation devices
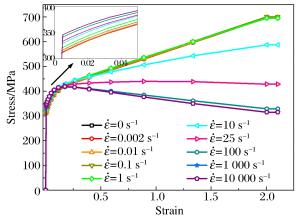
部件 材料 密度/(kg·m-3) 杨氏模量/GPa 屈服极限/MPa 破坏极限/MPa 泊松比 上端框 铝合金 2 700 70 311 485 0.33 下端框 铝合金 2 700 70 311 485 0.33 分离板 铝合金 2 700 70 311 485 0.33 膨胀管 不锈钢 7 900 184 196 540 0.33 螺栓 高强钢 7 750 184 835 1 080 0.33 
下载: 导出CSV
表 2 各测点x方向的加速度峰值
Table 2. Peak values of acceleration at x direction
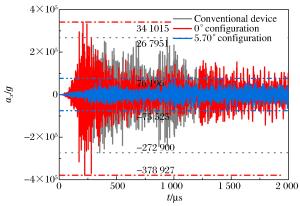
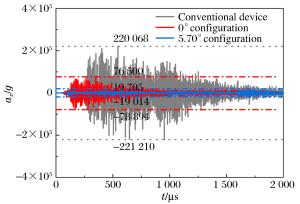
测点 ax/g 5.7°构型相对常规构型加速度峰值改变百分比 常规构型 0°构型 5.7°构型 1 272 900 378 927 76 196 ↓72% 2 210 815 217 501 44 516 ↓79% 3 303 699 194 720 49 743 ↓84%
下载: 导出CSV
表 3 各测点y方向的加速度峰值
Table 3. Peak values of acceleration at y directionc
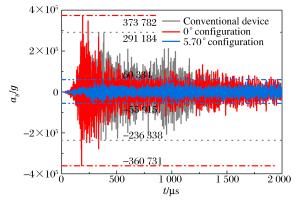
测点 ay/g 5.7°构型相对常规构型加速度峰值改变百分比 常规构型 0°构型 5.7°构型 1 291 184 373 782 60 334 ↓79% 2 192 707 259 129 80 457 ↓58% 3 204 263 187 374 68 198 ↓67%
下载: 导出CSV
表 4 各测点z方向的加速度峰值
Table 4. Peak values of acceleration at z direction
测点 az/g 5.7°构型相对常规构型加速度峰值改变百分比 常规构型 0°构型 5.7°构型 1 221 210 78 894 19 705 ↓91% 2 180 490 43 739 9 267 ↓95% 3 237 170 43 733 8 871 ↓96%
下载: 导出CSV
-
[1] 谢鲁.膨胀管分离装置研究[J].火工品, 1997, 2:1-6. http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201802004XIE Lu. Study on the expansion tube separating device[J]. Initiators & Pyrotechnics, 1997, 2:1-6. http://d.old.wanfangdata.com.cn/Periodical/bjlgdxxb201802004 [2] 谢鲁.膨胀管分离装置的研究[D].南京: 南京理工大学, 2005. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1000485 [3] 夏晓宇.火工分离装置工作过程性能分析[D].长沙: 国防科学技术大学, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1689790 [4] 王江, 李虹.线性分离装置分离性能仿真[J].强度与环境, 2011, 38(2):28-33. doi: 10.3969/j.issn.1006-3919.2011.02.006WANG Jiang, LI Hong. Simulation on the separating performance of linear separation system[J]. Structure & Environment Engineering, 2011, 38(2):28-33. doi: 10.3969/j.issn.1006-3919.2011.02.006 [5] 宋保永, 吴晗玲, 王帅, 等.膨胀管分离装置设计参数的敏感性分析[J].北京理工大学学报, 2013, 33(2):76-79.SONG Baoyong, WU Hanling, WANG Shuai, et al. Design parameter sensitivity analysis of super-zip separation devices[J]. Transactions of Beijing Institute of Technology, 2013, 33(2):76-79. [6] 宋保永, 胡振兴, 孙璟, 等.膨胀管分离装置分离时间测试研究[J].实验力学, 2015, 30(2):151-156. http://d.old.wanfangdata.com.cn/Periodical/sylx201502003SONG Baoyong, HU Zhenxing, SUN Jing, et al. On the measurement of the separation time of expanding tube separation device[J]. Journal of Experimental Mechanics, 2015, 30(2):151-156. http://d.old.wanfangdata.com.cn/Periodical/sylx201502003 [7] 孙璟, 阳志光.膨胀管分离装置爆炸分离过程仿真和优化[C]//第九届全国爆炸与安全技术学术会议.沈阳, 2006: 140-143. [8] 阳志光.航天运载器线式火工分离装置结构优化设计[D].北京: 北京工业大学, 2007. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1164589 [9] DREXELIUS V, LAKE E, SCHIMMEL M. Explosive severance means: US3486410[P]. 1969-12-30. [10] ANDERSON M, HEIDEMANN W. A study of an advanced confined linear energy source: NASA-CR-112096-19720022304[R]. 1972. [11] BRANDT O, HARRIS J. Explosive system: US3698281[P]. 1972-10-17. [12] NOEL V, VAN SHOUBROUEK F. Separation system: US004685376[P]. 1987-08-11. [13] FRITZ J. Separation joint technology[C]//39th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Huntsville, Alabama. 2003. [14] CLEVELAND M. Low shock separation joint and method therefore: WO2005040713A2[P]. 2005-05-06. [15] BLAIN J, NELSON R, GROSSKRUEGER D, et al. Separation system: US005969287[P]. 1999-10-19. [16] CLEVELAND M. Low shock separation joint and method therefore: US20050193916A1[P]. 2005-09-08. [17] CLEVELAND M. Low shock separation joint and method therefor: US007261038B2[P]. 2007-08-28. [18] GOLDEN P, BEAUDOIN J, HOSKINS R, et al. Low shock rocket body separation: US008607705B2[P]. 2013-12-17. [19] HAN C, SUN C. Attenuation of stress wave propagation in periodically layered elastic media[J]. Journal of Sound and Vibration, 2001, 243(4):747-761. doi: 10.1006/jsvi.2000.3420 [20] HUI D, DUTTA P. A new concept of shock mitigation by impedance-graded materials[J]. Composites:Part B, 2011, 42:2181-2184. doi: 10.1016/j.compositesb.2011.05.016 [21] NEMAT-NASSER S, AMIRKHIZI A. Microstructural design for stress wave energy management: ONR N00014-09-1-0547[R]. 2013. [22] RAFIEE-DEHKHARGHANI R. Stress wave scattering in solids for mitigating impulsive loadings[D]. New York: the State University of New York at Buffalo, 2014. http://search.proquest.com/docview/1658211289 [23] RAFIEE-DEHKHARGHANI R, AREF A, DARGUSH G. Characterization of multilayered stress wave attenuators subjected to impulsive transient loadings[J]. Journal of Engineering Mechanics, 2015, 141(4):04014137. doi: 10.1061/(ASCE)EM.1943-7889.0000859 [24] NEMAT-NASSER S, SADEGHI H, AMIRKHIZI A, et al. Phononic layered composites for stress-wave attenuation[J]. Mechanics Research Communications, 2015, 68:65-69. doi: 10.1016/j.mechrescom.2015.05.001 [25] RAFIEE-DEHKHARGHANI R, AREF A, DARGUSH G. Planar stress wave attenuation in plates with circular voids and inclusions[J]. Composites:Part B, 2015, 75:307-318. doi: 10.1016/j.compositesb.2015.01.051 [26] 任怀宇.粘弹阻尼减振在导弹隔冲击结构中的应用[J].宇航学报, 2007, 28(6):1494-1499. doi: 10.3321/j.issn:1000-1328.2007.06.011REN Huaiyu. The application of viscoelastic damping vibration suppression for shock-isolation structure of multistage missile[J]. Journal of Astronautics, 2007, 28(6):1494-1499. doi: 10.3321/j.issn:1000-1328.2007.06.011 [27] 王贤宙.粘弹性阻尼安装架结构设计及减振效能分析[J].电子机械工程, 2015, 31(1):35-38. doi: 10.3969/j.issn.1008-5300.2015.01.008WANG Xianzhou. Structure design and vibration reduction performance analysis of viscoelastic damping mounting rack[J]. Electro-Mechanical Engineering, 2015, 31(1):35-38. doi: 10.3969/j.issn.1008-5300.2015.01.008 [28] HOOPUTRA H, GESE H, DELL H, et al. A comprehensive failure model for crashworthiness simulation of aluminium extrusions[J]. International Journal of Crashworthiness, 2004, 9(5):449-464. doi: 10.1533/ijcr.2004.0289 [29] Dassault Systèmes. Progressive failure analysis of thin-wall aluminum extrusion under quasi-static and dynamic loads[Z]. Abaqus Example Problems Manual, 2011. 期刊类型引用(1)
1. 冯丽娜，李东，田建东，陈楷. 低冲击剪切式膨胀管分离装置设计与分析. 宇航总体技术. 2022(05): 62-70 . 
百度学术其他类型引用(0)
-
百度学术
计量
- 文章访问数: 5586
- HTML全文浏览量: 1270
- PDF下载量: 35
- 被引次数: 1