Application of multi-objective optimization algorithm to motional simulation of bullets penetrating ballistic gelatin
-
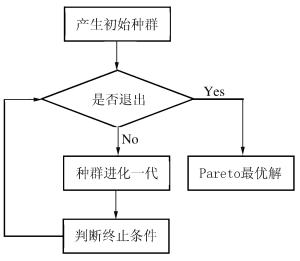
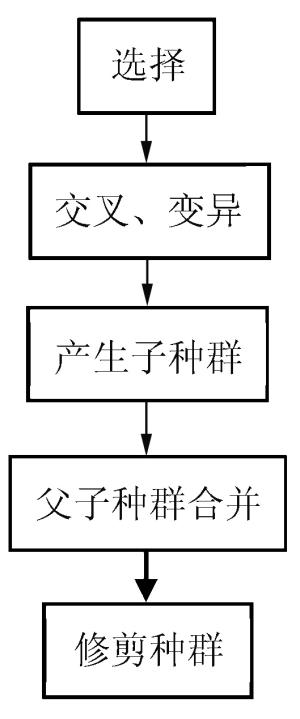
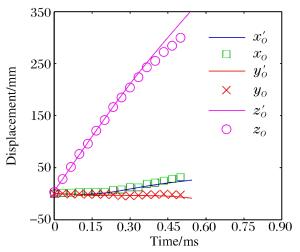
摘要: 为使弹道模型更好地模拟弹头侵彻明胶的运动规律，从而有助于揭示弹头对人体组织的致伤机理，以弹头水平位移、竖直位移、侧向位移、俯仰角以及偏航角理论值的均方根误差作为目标函数组，以弹头的待定初始运动参数和弹道模型的待定力学系数作为优化变量，通过Gamultiobj多目标遗传算法获得了的优化变量的Pareto解集，并通过TOPSIS综合分析方法获得了Pareto解集的最优解。研究结果表明该方法能够快速获得可信性较强的最优解，使最优解能较好地模拟7.62 mm步枪弹侵彻明胶的运动过程。Abstract: To find out about the wounding mechanisms of bullets penetrating human bodies, we simulated in this work the processes of bullets penetrating ballistic gelatin using the ballistic model. By taking the root mean squares of the theoretical errors of the horizontal displacements, the vertical displacements, the lateral displacements, the pitch angles and the yaw angles as the objective functions, treating the undetermined initial parameters of the bullet and the force coefficients in the ballistic model as the optimization variables, and using the Gamultiobj method, one of the multi-objective algorithms, we successfully found the set of the Pareto solutions to the objective functions, and selected the optimum solution to the optimization variables through the TOPSIS strategy from the Pareto solutions. Our studies show that the optimum solution is reliable and can present precise simulation of the motions of the 7.62 mm rifle bullet.
-
Key words:
- multi-objective optimization /
- rifle bullet /
- gelatin /
- penetration
-
含铝炸药有较高的爆热和较强的作功能力，成为含能材料领域的研究热点。含铝炸药能量释放特性与理想炸药较大的不同主要在于，铝粉通常在CJ面后与气相产物发生二次反应，且随着铝粉含量的增加，含铝炸药的爆速降低[1-3]。铝粉的表面被一层氧化铝薄膜所覆盖，厚度通常为3～5 nm[4]，铝粉反应通常发生在氧化铝膜破裂后。含铝炸药中铝粉的反应延滞时间为爆轰波到达后铝粉氧化膜发生破裂且与气相产物发生反应所需要的时间，而铝粉氧化膜的破裂与多种因素有关（如铝核升温、熔化导致的热应力，氧化铝膜晶变、熔化，冲击波的作用导致的颗粒变形等）。研究含铝炸药中铝粉的反应起始时间，可以加深认识含铝炸药中铝粉的反应过程，为含铝炸药配方设计及应用提供参考。
低压下的铝粉燃烧实验表明，铝粉的燃烧时间与铝粉粒度之间满足dn关系[5]。由于含铝炸药爆轰时的高温、高压，很难直接测量产物中铝粉的反应情况，通常通过宏观爆轰性能测试，反推炸药中的铝粉反应情况。含铝炸药中铝粉的反应速率的实验研究主要有光谱法[6-8]、圆筒实验法[9-10]、飞片撞击法[11-12]、水下爆炸法等[13-14]，由以上方法已得到一些定性认识（如铝粉的反应与约束条件，炸药组分，铝颗粒的尺寸、形状等相关），而对于炸药中铝粉反应的时间尺度，目前尚未形成较统一的认识。对铝粉二次反应起始时间已进行了一定的研究。曾亮等[15]利用电导率方法，对TNT/Al炸药中铝粉的反应起始时间进行了测量，结果表明粒径2、10 μm铝粉的反应起始时间分别为0.4、1.5 μs。Tao[16]利用激光速度干涉仪，分别测量了PETN和TNT含铝炸药与窗口的界面粒子速度，并依此标定了炸药的点火增长模型参数，进而计算了炸药的反应速率，并通过计算结果推断，粒径5 或18 μm铝粉会在1.5 μs内与PETN炸药的爆轰产物完全反应。Manner等[17]对HMX/Al（粒径3.2 μm）和HMX/LiF炸药进行了圆筒实验，结果表明2 μs内铝粉发生了显著的反应。Chan[18]对含铝炸药中铝粉的反应起始时间进行理论分析，认为当铝颗粒表面温度超过高压下铝的熔点时铝粉开始反应，则10 μm铝粉的反应起始时间为0.1 μs。以上大部分研究表明，微米级铝粉的反应起始时间在2 μs以内，但不同研究者给出的铝粉反应的具体起始时间差异较大，还有待进一步研究。
利用激光干涉法测量炸药与窗口的界面速度，可以获得炸药的爆轰波结构，进而可以分析反应区附近铝粉的反应情况，相比飞片法、圆筒实验法等，界面粒子速度法的结构响应更快（纳秒级）。本文中，将测量两种RDX/Al炸药和一种RDX/LiF炸药的爆轰波结构，分析爆轰产物中铝粉的反应延滞时间及反应区附近铝粉的反应情况，拟为爆轰产物环境下铝粉的反应动力学建模提供参考。
1. 实 验
测试系统主要由火炮、蓝宝石飞片、待测炸药、LiF光学窗口、光纤测速探头和光子多普勒测速仪（photon Doppler velocimetry, PDV）等组成，如图1所示。利用口径57 mm的火炮发射蓝宝石飞片撞击炸药产生一维平面波。在炸药背面安装
∅ 20 mm×11 mm的LiF窗口，LiF窗口与炸药接触面有厚约0.7 μm的铝镀膜。如图2所示，在背部靶架上安装3个光纤探头P1、P2和P3（在图1中仅示意P1），其中P1探头焦点正对炸药中心，P2和P3对称分布在P1两侧，与中心距离均为3.8 mm。在实验记录的时间内，被测区域不受侧向稀疏波的影响，始终为一维平面爆轰波。实验前，将炸药安装在爆炸罐中的炮管正前方，通过爆炸罐上的光纤法兰连接测试用探头与罐外仪器，最后对爆炸罐抽真空。光子多普勒测速仪为中国工程物理研究院流体物理研究研制，测速范围上限可达9 km/s。采用窗口傅里叶变换方法处理数据，速度时间分辨率为3 ns。不确定度主要由PDV测试的不确定度、窗口和探头安装导致的不确定度、炸药不均匀导致的不确定度3方面决定 ，速度的相对合成标准不确定度为2%。
由于炸药与LiF的阻抗有差别，实验测得的界面粒子速度并非炸药稳定爆轰时的波后粒子速度。因此，可利用冲击阻抗匹配公式计算炸药反应区内的压力[19]：
pCJ=12uCJ(ρ0(c0+λuCJ)+ρDCJ) (1) 式中：pCJ为待测炸药的爆压，uCJ为CJ点对应的界面粒子速度，ρ0为窗体材料初始密度，c0为窗体材料初始声速，λ为窗体材料冲击绝热线常数，ρ为待测炸药初始密度，DCJ为待测炸药CJ爆速。
采用压装工艺，制备了3种RDX基炸药，配方见表1。药柱的尺寸为
∅ 40 mm×30 mm。其中，铝粉为球形，粒径分别为2和10 μm，纯度大于99.8%；氟化锂粉末平均粒径为2.5 μm，纯度大于99%。氟化锂的密度、冲击阻抗、分子量与铝比较接近，且其化学性质较稳定，不会与炸药气相产物发生反应，在炸药产物中主要以惰性物质形式存在。通过含氟化锂炸药与含铝炸药的对比，可以评估铝粉的反应情况。铝和氟化锂的主要物理参数见表2，表中Tm、Tb、cV和K分别为熔点、沸点、比定容热容和导热系数。表 1 三种RDX基炸药的配方和参数Table 1. Components and characteristics of three kinds of explosives炸药 w/% 粒径/μm 密度/(g·cm−3) D/(m·s−1) RDX Al LiF 黏合剂 RF15 80 0 15 5 2.5 1.809 8141±40 RA15(2 μm) 80 15 0 5 2.0 1.803 8072±40 RA15(10 μm) 80 15 0 5 10.0 1.795 8070±40 表 2 铝和氟化锂的物理参数对比Table 2. Comparison of the main characteristics of Al and LiF材料 ρ0/(g·cm−3) Tm/K Tb/K cV/(J·g−1·K−1) K/(W·m−1·K−1) c0/(km·s−1) λ 铝 2.700 933 2 740 1.176 210 5.325 1.338 氟化锂 2.638 1 143 1.513 11.3 5.176 1.359 2. 结果与分析
2.1 界面粒子速度
对3种炸药均做了1发实验。实验中，测量了蓝宝石飞片速度，结果为(1 256±30) m/s；根据蓝宝石和待测炸药冲击绝热线，计算可得炸药中的输入压力约为8 GPa；该压力下炸药的到爆轰距离约为3 mm，可得到炸药稳定爆轰的传播距离约为27 mm。图3为实验测得的炸药爆轰波界面速度，每发实验均获得了3个数据。同一炸药不同探头之间的速度曲线差异较小，表明测试精度较高。
2.2 铝粉反应起始时间
每发实验3个位置的界面粒子平均值如图4所示。单个探头速度的相对不确定度为2%，多个探头速度平均值的相对不确定度约为1%。由图4可见，在CJ点前的反应区内，3种炸药的界面粒子变化趋势较一致，为了更清晰地呈现这个变化趋势，对CJ点附近的曲线进行了放大，如图5所示。由图5可见，von Neumann峰处3种炸药的界面粒子速度为1.8～1.9 km/s，在随后的15 ns内速度迅速下降到约1.6 km/s，该过程对应着RDX的分解反应。Pei等[20]对RDX基PBX炸药的爆轰反应区进行了测量（见图6），得到稳态爆轰条件下RDX基PBX炸药的爆轰反应时间为(14±3) ns，与本文含铝炸药的测试结果基本一致。由于铝粉与气相爆轰产物间的反应属于分子间的反应，在如此短的时间内，铝粉难以发生反应，可以认为RDX完全分解的点即为CJ点；考虑测试误差，可以认为3种炸药CJ点的速度均为(1 640±20) m/s，可计算3种炸药的爆压为27.6 GPa，对应CJ点等熵绝热指数为3.26。CJ点后到0.5 μs，含LiF炸药的界面粒子速度始终高于含铝炸药的，这是因LiF粉末与铝粉间的热力学性质差异导致。
图 4 三种炸药的平均界面粒子速度曲线Figure 4. Average interface particle velocity curves of three explosives
图 5 CJ点附近三种炸药的平均界面粒子速度曲线Figure 5. Average of interface particle velocitiy curves of three explosives near the CJ point在CJ点附近，气相爆轰产物与固体添加物之间会发生动量和热量的交换[21]。动量的交换主要与固相产物的冲击阻抗相关，因此，铝粉和LiF粉末之间的差异较小。而热量的交换主要与添加物的导热系数及颗粒粒径相关，铝的导热系数为210 W/(m·K)，远大于LiF的导热系数11.3 W/(m·K)，因此，在反应区附近，LiF粉末吸收的热量更少，对应的产物动能更大，相应的产物界面粒子速度也更高。含铝炸药和含LiF炸药界面粒子速度差最大出现在170 ns，此时，含LiF炸药的界面粒子速度为1 544 m/s，比含铝炸药的界面粒子速度1 455 m/s高7%。
随后，含铝炸药与含LiF炸药的界面粒子速度差越来越小，在0.6 μs时含2 μm铝炸药的界面粒子速度开始超过含LiF炸药的，在0.8 μs时含10 μm铝炸药的界面粒子速度开始超过含LiF炸药的。这表明，该时间段内，铝粉已经发生了反应。在0.4 μs时含2 μm铝炸药的界面粒子速度开始超过含10 μm铝炸药的，两者速度差最大出现在0.72 μs时，此时含2 μm铝炸药的界面粒子速度为1 308 m/s，比含10 μm铝炸药的界面粒子速度（1 257 m/s）高4%。这表明，铝粉粒径越小，炸药反应延滞时间越短。综合以上，两种粒度含铝炸药反应延滞时间为0.4～0.8 μs。在1.3 μs时含2和10 μm铝炸药的界面粒子速度分别为1 110和1 082 m/s，比含LiF炸药的界面粒子速度1 004 m/s分别提高了11%和8%，这时反应已经比较显著。
2.3 铝粉反应度
在铝粉反应的初始阶段，含铝炸药与含LiF炸药的主要成分相似，因此以含LiF炸药的等熵形式状态方程作为参考线，构建含铝炸药的状态方程[22]：
p(e,v)=pS,RF15(v)+Γ(v)v(e−eS,RF15(v))=pS,RF15(v)+Γ(v)vQλ (2) 式中：Q为铝粉与气相爆轰产物反应释放的总能量，
λ 为铝粉的反应度，Γ(v) 为爆轰产物Grüneisen系数，v为爆轰产物相对比容。为了分析铝粉的反应情况，需要联系界面粒子速度与炸药的状态方程。在反应区，铝粉反应产生的压力变化为弱扰动波，该条件下，以含LiF炸药为参考，铝粉反应产生的压力变化与界面粒子速度有关系：
Δp=p(e,v)−pS,RF15(v)=ρcΔu (3) 式中：ρ为炸药产物的密度，c为产物的声速，
Δu 为因铝粉反应导致的界面粒子速度变化。联立式(2)～(3)，可得：
λ=cΔuΓ(v)Q (4) 产物的压力同时受比容（决定冷压）和内能（决定热压）的影响，为便于分析内能对产物压力的影响，并分析铝粉的反应放能情况，本文中选择比容相同的时刻，以排除产物比容对产物压力的影响。为此，对炸药的界面粒子速度进行积分，如图7所示。选取界面粒子速度位移相同的时刻（比容相同）：炸药RA15 (10 μm)与RF15比容相同的时刻为1.1 μs，对应的界面粒子速度差为81 m/s；炸药RA15 (2 μm)与RF15比容相同的时刻为1.3 μs，对应的界面粒子速度差为74 m/s。为了获得上述时刻产物的密度、比容，针对本文的实验模型进行了数值模拟，其中炸药RF15的状态方程数据通过圆筒实验[9]拟合获得，数值模拟的炸药界面粒子速度如图8所示。初期，数值模拟的界面粒子速度与实验结果有一定差异，这是因数值模型中没有考虑炸药的反应过程而仅采用了产物的状态方程；在150 ns后，数值模拟结果与实验结果一致性较好。通过数值模拟，获得在1.1和1.3 μs时产物的相对比容v分别为0.86和0.89。
图 8 实验和模拟的炸药RF15界面粒子速度曲线Figure 8. Experimental and simulated interface particle velocity curves of explosive RF15爆轰产物的声速为：
c=√∂p∂ρ=(ρ0ρ2(AR1exp(−R1V)+AR2exp(−R2V)+C(1+ω)V−(2+ω)))1/2 (5) 在1.1和1.3 μs时，c分别为5 444和5 277 m/s，Q为1.8 ～3.0 MJ/kg，则炸药RA15 (2 μm)在1.1 μs时的反应度为18.4%～30.6%，炸药RA15 (10 μm)在1.3 μs时的反应度为16.3%～27.1%，两者的差距较小。由低压下铝粉燃烧实验，铝粉的燃烧时间t与铝粉的初始粒度d之间满足t=dn关系，n通常为1～2。取n为1，由该公式，2和10 μm铝粉炸药的反应度应有显著差异。而本文的结果与之不同，这说明爆轰产物环境下铝粉的反应机制与低压下铝粉的燃烧过程有较大差异。Li等[23]利用圆筒实验研究了铝粉粒度对铝粉反应速率的影响，结果表明，因爆轰产物中铝颗粒的破碎，铝粉颗粒大小对反应速率影响较小。本文的结果与圆筒实验结果[23]基本一致。
3. 结 论
(1)含铝炸药爆轰波结构与理想炸药有较大差异，其界面粒子速度曲线没有明显的拐点，反应初期因气相产物与添加物之间温度、速度的非平衡性，RDX/Al炸药的界面粒子速度低于RDX/LiF炸药的，随后因铝粉反应放能，使RDX/Al炸药的界面粒子速度高于RDX/LiF炸药的。
(2)微米铝粉在CJ面前不发生反应，2、10 μm铝粉RDX/Al炸药的爆轰波结构没有明显差异， 二者的反应延滞时间小于0.8 μs。
(3)爆轰产物环境下铝粉的反应机制与低压下有较大差异，反应速率受铝粉粒度的影响不明显，在本文中，两种粒度铝粉炸药的反应度为16%～31%。结果可提升对含铝炸药中铝粉反应过程的认识，为爆轰产物环境下铝粉的反应动力学建模提供参考。
-
表 1 待优化力学系数的取值范围
Table 1. Bounds of undetermined mechanical coefficients
边界 CD0 C1 CL0 CM0 下界 0 0 0 0 上界 0.1 15.0 1.0 0.2 
下载: 导出CSV
表 2 待优化力学系数的最优解
Table 2. Optimum solutions of undetermined mechanical coefficients
序号 C1 CD0 CL0 CM0 vx0/
(m·s-1)vy0/
(m·s-1)vz0/
(m·s-1)θ0/
(°)ψ0/
(°)θt0/
(rad·s-1)ψt0/
(rad·s-1)φt0/
(rad·s-1)1 7.49 0.058 6 0.636 0.064 7 -22.4 -14.20 713 1.910 68.8 1 020 1 220 15 400 2 8.89 0.066 2 0.669 0.082 9 15.3 -17.40 703 0.115 68.8 1 470 1 910 17 600 3 7.72 0.051 3 0.744 0.091 1 23.5 4.10 720 0.281 81.4 1 220 2 200 19 100 4 10.90 0.064 2 0.723 0.071 9 18.3 7.73 717 0.728 81.9 1 410 1 840 12 800 5 4.83 0.047 8 0.813 0.062 8 15.6 -16.90 715 0.682 70.5 1 750 2 260 16 900
下载: 导出CSV
表 3 最优解对应的目标函数值
Table 3. Values of objective functions corresponding to optimal solutions
序号 σ(1)/mm σ(2)/mm σ(3)/mm σ(4)/(°) σ(5)/(°) 1 2.22 1.59 9.54 5.47 5.02 2 2.35 1.53 6.90 5.39 9.50 3 4.09 1.97 12.1 7.22 11.6 4 3.91 1.65 7.28 11.6 4.30 5 6.79 1.73 12.4 5.42 6.26
下载: 导出CSV
-
[1] KNEUBUEHL B P, COUPLAND R M, ROTHSCHILD M A, et al. Wound ballistics, basics and applications[M]. New York:Springer, 2011:136-143. [2] 刘荫秋, 王正国, 马玉媛.创伤弹道学[M].北京:人民军医出版社, 1991:30-33. [3] 程可.轻武器杀伤元对明胶靶标侵彻的数值仿真研究[D].南京: 南京理工大学, 2012: 15-19. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2061965 [4] LIU S S, XU C, CHEN A J, et al. Effect of rifle bullet parameters on the penetration into ballistic gelatin[J]. Journal of Beijing Institiute of Technology, 2015, 24(4):487-493. DOI: 10.15918/j.jbit1004-0579.201524.0409. [5] WEN Y, XU C, JIN Y, et al. Rifle bullet penetration into ballistic gelatin[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2016, 67:40-50. DOI: 10.1016/j.jmbbm.2016.11.021. [6] 温垚珂, 徐诚, 陈爱军, 等.步枪弹侵彻明胶靶标的数值模拟[J].兵工学报, 2013, 34(1):14-19. DOI: 10.3969/j.issn.1000-1093.2013.01.003.WEN Yaoke, XU Cheng, CHEN Aijun, et al. Numerical simulation of the penetration of bullet on gelatin target[J]. Acta Armamentarii, 2013, 34(1):14-19. DOI: 10.3969/j.issn.1000-1093.2013.01.003. [7] DATOC D. Finite element analysis and modeling of a.38 lead round nose ballistic gelatin test[D]. Ponoma: California Polytechnic State University, 2010: 20-55. [8] WANG Y, SHI X, CHEN A, et al. The experimental and numerical investigation of pistol bullet penetrating soft tissue simulant[J]. Forensic Science International, 2015, 249C:271-279. DOI: 10.1016/j.forsciint.2015.02.013. [9] YOON G H, MO J S, KIM K H, et al. Investigation of bullet penetration in ballistic gelatin via finite element simulation and experiment[J]. Journal of Mechanical Science and Technology, 2015, 29(9):3747-3759. DOI: 10.1007/s12206-015-0821-7. [10] 刘坤, 吴志林, 徐万和, 等.弹头侵彻明胶的运动模型[J].爆炸与冲击, 2012, 32(6):616-622. doi: 10.3969/j.issn.1001-1455.2012.06.010LIU Kun, WU Zhilin, XU Wanhe, et al. A motion model for bullet penetrating gelatin[J]. Explosion and Shock Waves, 2012, 32(6):616-622. doi: 10.3969/j.issn.1001-1455.2012.06.010 [11] LIU S, XU C, WEN Y, et al. A new motion model of rifle bullet penetration into ballistic gelatin[J]. International Journal of Impact Engineering, 2016, 93:1-10. DOI: 10.1016/j.ijimpeng.2016.02.003. [12] 莫根林, 吴志林, 冯杰, 等.步枪弹侵彻明胶的表面受力模型[J].兵工学报, 2014, 35(2):164-169. DOI: 10.3969/j.issn.1000-1093.2014.02.004.MO Genlin, WU Zhilin, FENG Jie, et al. Surface pressure model of rifle bullets penetrating into ballistic gelatin[J]. Acta Armamentarii. 2014, 35(2):164-169. DOI: 10.3969/j.issn.1000-1093.2014.02.004. [13] 戴光明, 王茂才.多目标优化算法及在卫星星座设计中的应用[M].湖北:中国地质大学出版社, 2009:1-9. [14] 崔逊学.多目标进化算法及其应用[M].北京:国防工业出版社, 2008:48-70. [15] 张延教.高等动力学[M].南京:华东工程学院, 1984:56-280. [16] 郁磊.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社, 2015:89-101. [17] 杨路春, 李学斌, 丁明君, 等.多目标遗传算法和决策在船型论证中的应用[J].哈尔滨工程大学学报, 2012, 33(12):1459-1464. DOI: 10.3969/j.issn.1006-7043.201203053.YANG Luchun, LI Xuebin, DING Mingjun, et al. Application of multi-objective genetic algorithm and decision-making skills in ship form evaluation[J]. Journal of Harbin Engineering University, 2012, 33(12):1459-1464. DOI: 10.3969/j.issn.1006-7043.201203053. [18] 叶义成, 柯丽华, 黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社, 2006:52-56. [19] 高乃同.自动武器弹药学[M].北京:国防工业出版社, 1990:334-336. 期刊类型引用(2)
1. 纪玉国，张国凯，李干，邓树新，姚箭，李杰，王明洋，何勇. 坑道内爆炸条件下温压炸药的爆炸特性及其影响因素. 爆炸与冲击. 2024(03): 118-132 . 
本站查看2. 杨峰，翟红波，苏健军，李尚青，肖洋，刘伟. TNT和温压炸药浅埋爆炸效应差异性研究. 兵器装备工程学报. 2024(05): 160-166 . 
百度学术其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 4825
- HTML全文浏览量: 1554
- PDF下载量: 45
- 被引次数: 3