Investigation of the propagation modes for gaseous detonation at near-limit condition
-
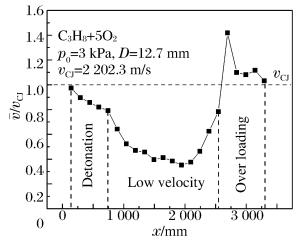
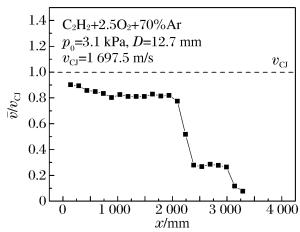
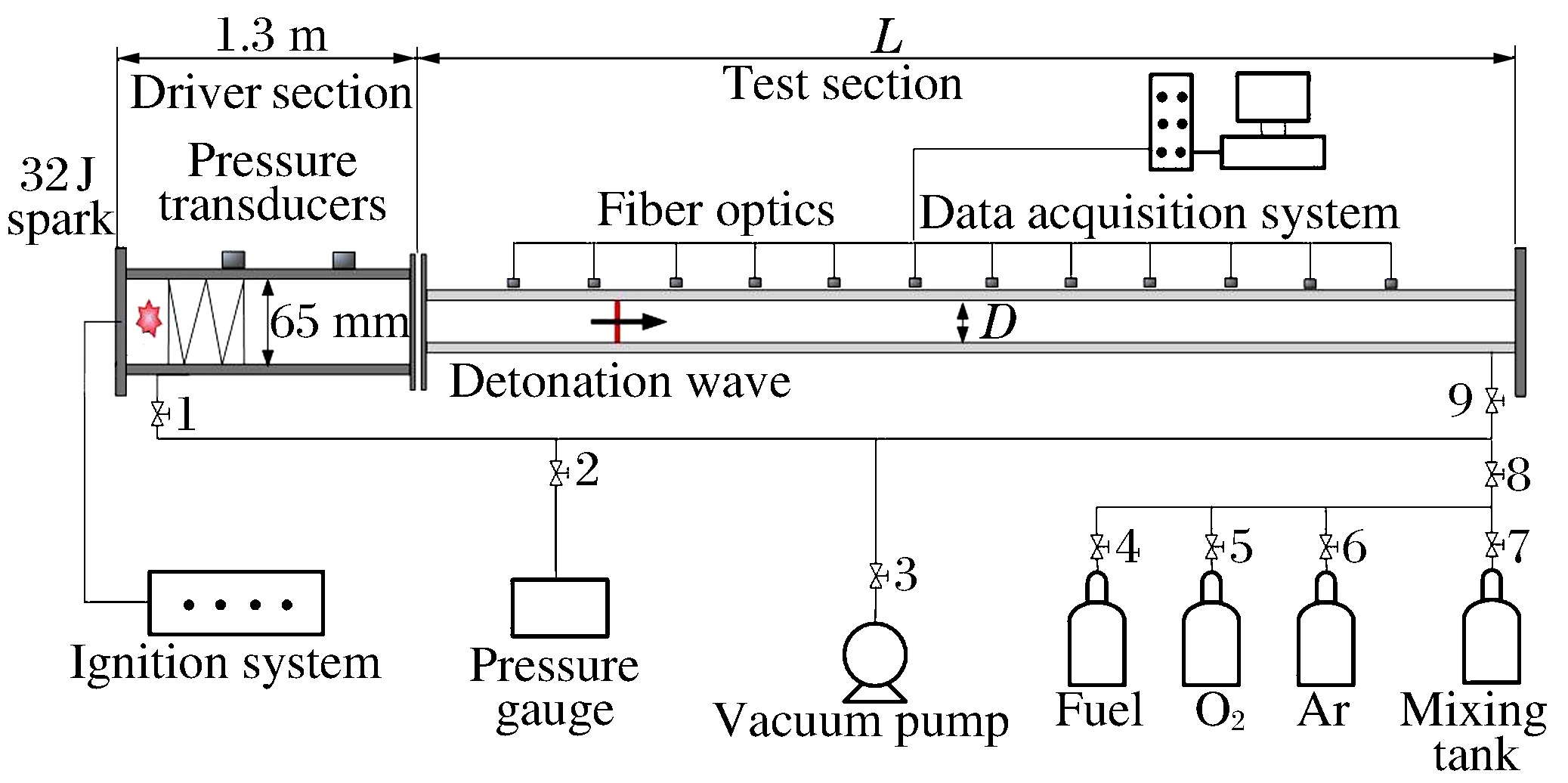
摘要: 选用五种碳氢混合气体，采用高压电火花起爆的方法，利用光纤探针测量爆轰波在管道内的传播速度，研究临近失效状态时爆轰波在管道内的传播模式。实验是在自行研制的爆轰管道中进行的，其包括驱动段及内径分别为1.5、3.2、12.7 mm三种规格的测试段。实验结果再次验证了爆轰波在管道内传播时可以有六种不同的传播模式：稳态爆轰、快速波动爆轰、结巴式爆轰、驰振爆轰、低速爆轰和爆轰失效。其中C2H2+2.5O2+70% Ar、C2H2+2.5O2+85% Ar两种组分混合气体（具有较低活化能），在爆轰波传播过程中只有稳态、快速波动和失效三种模式；而C3H8+5O2、C2H2+5N2O和CH4+2O2三种组分混合气体（具有较高活化能）在传播过程中出现六种不同模式。上述结果表明，除气体组分、初始压力等因素外，混合气体的活化能可能对爆轰波在管道内的传播状态也有影响。Abstract: In this paper, five kinds of hydrocarbon gaseous mixture were selected as working medium. By using high voltage spark ignition method and optical fiber probe, the propagation velocity of detonation wave in pipeline was measured near failure state condition. Experiments were conducted based on a self-made detonation pipeline, which includes a drive section and three different test sections with 1.5-mm, 3.2-mm and 12.7-mm inner diameter, respectively. Experimental results reverified that there are six different propagation modes, which are steady detonation, rapid fluctuation detonation, stuttering detonation, galloping detonation, low velocity detonation and detonation failure, respectively for pipeline detonation. Among them, gaseous mixtures C2H2+2.5O2+70%Ar and C2H2+2.5O2+85%Ar (both have low activation energy), have only three propagating modes, i.e. steady, rapid fluctuation and failure modes; while for other three gaseous mixtures C3H8+5O2, C2H2+5N2O and CH4+2O2 (with higher activation energy), there are six different propagating modes. The results show that besides gas composition and initial pressure, the activation energy of gaseous mixture may also affect the propagation state of detonation wave in pipeline.
-
Key words:
- detonation wave /
- propagation mode /
- velocity fluctuation /
- activation energy
-
脉冲爆轰发动机(pulse detonation engine, 简称PDE)是一种利用脉冲式爆轰波产生推力的新概念发动机，具有热效率高、结构简单等优点。多管PDE的构想最早出现在20世纪50年代，相对于单爆轰管的PDE，增加爆轰管数量具有增加推力和提高工作频率等优点。国内外对多爆轰管PDE研究颇有成效，2014年T.Morozumi等[1]采用乙烯为燃料，N2O为氧化剂，实现了四爆轰管PDE装置的成功起飞，工作过程中对称的两爆轰管同时起爆，在1500 ms的工作过程中测得平均推力为256 N，比冲为130.8 s。2011年，袁成等[2]以汽油为燃料，空气为氧化剂，成功实验了六个爆轰管的吸气式PDE的多循环起爆。然而作为一种动力装置，其在工作过程中产生较大的噪声会引起结构的声疲劳、对相关工作人员的听力造成损伤、对周围环境产生噪声污染等危害。因此，对多爆轰管PDE爆轰噪声的研究具有重要意义。
针对单爆轰管PDE爆轰噪声特性已有一系列的研究报道，L.Shaw等[3]对距离出口0~3.66 m范围内的PDE管外噪声进行了测量，发现距离管口越近，声压级越高。通过信号频率的处理，发现随着距管口的距离的增加，由于高频噪声在大气中的耗散作用，其声压的幅值迅速衰减。美国辛辛那提大学A.Glaser等[4]对距离出口方向不同角度、不同轴向距离的PDE爆轰噪声进行了实验，发现爆轰噪声辐射具有一定的指向性，并且得出了噪声幅值随轴向距离变化的衰减规律。国内对于PDE爆轰噪声的实验研究相对较少。郑龙席等[5]进行了气液两相PDE噪声实验研究，发现其噪声辐射呈现间歇性和周期性的特点，噪声源主要由单极子源和四极子源组成；噪声辐射的频谱为宽频带谱，其能量主要集中在低频部分，由气流脉动的基频和谐频组成；峰值声压级与爆轰频率无关，而脉冲声压级、声功率级和声功率随爆轰频率的增加而提高。许桂阳等[6]对加装不同喷管的PDE爆轰噪声进行了实验研究，发现加装喷管可以降低爆轰噪声和减小爆轰噪声的参考半径。
对于多管PDE爆轰噪声的研究，美国辛辛那提大学N.Caldwell等[7]对双爆轰管的PDE爆轰噪声进行了相关的实验研究，与单爆轰管PDE相比，双爆轰管PDE在距离管口2.89 m处产生的声压级要高出至少3 dB，并且爆轰噪声辐射的指向性更加明显。当前，国内多管PDE爆震噪声的研究尚未见到报道。
在前人研究的基础上，本文中着重于对正三角形这一典型多爆轰管组合方式的PDE爆轰噪声展开研究，通过实验探索多循环三爆轰管PDE近场噪声特性，分析其波形特征与衰减规律，得到爆轰噪声峰值衰减系数，并对噪声辐射指向性和持续时间进行研究。研究结果有助于探索多爆轰管PDE爆轰的噪声形成和传播机理以及多爆轰管PDE爆轰噪声的控制方法。
1. 实验系统
三爆轰管PDE实验系统如图 1所示，主要包括PDE、供气系统、供油系统、点火控制系统和测试系统等。
以压缩空气和压缩氧气作为氧化剂，燃料为93#汽油。3个爆轰管直径均为80 mm，摆放成正三角形样式，如图 1所示，中心轴间距为200 mm。PDE管头部以径向方式进气，通过精细雾化喷嘴和文氏管实现汽油雾化，并在混合室内实现氧化剂和燃料充分均匀混合。采用高能点火头，通过时序控制，实现三爆轰管同时起爆，点火频率为8 Hz，实验在常温常压下进行。在每个爆轰工作循环间隙内，会有新鲜燃料和氧化剂的混合物吹扫废气，同时达到完全填充PDE管，此时下一次点火开始，进行下一次工作循环。测试系统中的传感器为PCB公司高频动态传感器，传感器布置在垂直于爆轰管中心轴连线的水平面内0°、30°、45°和90°方向上，高度与图 1中正三角形中心点保持一致。在同一工况下，分别对距PDE出口400、600、800、1 000、1 200、1 600、2 400和3 000 mm处的噪声进行测试。测试得到的噪声电信号通过信号调理器处理后由同步数据采集系统采集，采样率为5×105 s-1。
2. PDE近场爆轰噪声传播特性分析
2.1 三管爆轰发动机爆轰噪声参考半径的变化
以r0为参考半径，将PDE噪声场划分为近场和远场，计算公式为[4]：
r0=(Ep0)13 (1) 式中：r0为参考半径, E为爆炸能量, p0为大气压力。定义r为距离三爆轰管名义“中点”的直线距离。当r＜r0时，PDE爆轰噪声峰值的衰减与r的倒数满足3次方变化规律，而在参考半径r0之外时，PDE爆轰噪声峰值的衰减与r的倒数满足1次方变化规律:
p peak ={k(r0r)3r⩽r0k1r0rr>r0 (2) 式中：k、k1为衰减系数。
因此，参考半径r0对PDE爆轰噪声机理研究具有重要意义。图 2为不同方向上PDE爆轰噪声幅值随距离r的变化曲线。其中实线为负3次方拟合曲线，虚线为负1次方拟合曲线。
图 2 爆轰噪声峰值随距离r变化的拟合曲线Figure 2. Fitted curves of detonation noise amplitudes varying with different distancesPDE近场爆轰噪声峰值ppeak与r的倒数满足一定的变化规律[4](公式(2))。
由曲线拟合情况可以看出：在距离管口较近的区域，三爆轰管PDE噪声场中的幅值衰减较快，衰减速度与1/r的3次方成正比。衰减速度逐渐放缓，在距离管口较远的地方，衰减速度与1/r成正比。这主要是因为在管口附近，管内爆轰波退化形成的高强度的激波和高温高压燃烧产物迅速喷出管口形成高压力区。伴随着高强度冲击波的迅速衰减和高温高压区的迅速扩散，压力幅值迅速下降。随着冲击波继续向前传播，冲击波强度逐渐减弱，其衰减速度也减慢。而中间距离的测试点，既不符合3次方，也不符合1次方的衰减规律。可将此区域定义为过渡区[8]，即由强非线性声场向弱非线性声场衰减的过渡区域。该区域内，冲击波强度迅速衰减，并且衰减速度逐渐放缓，最终由衰减逐步蜕变为弱非线性声波，其声压的衰减速度较快且规律性较差。根据公式(2)，以两条曲线的交汇点定义出参考半径r0，由0°、30°、60°和90°等4个方向的拟合曲线可以看出，参考半径r0≈0.7 m。本文中实验所用的爆轰管的直径d=80 mm，因此参考半径r0≈9倍管径。求得在0°、30°、60°和90°下，3次方衰减系数k=5.13×10-2、9.13×10-2、8.42×10-2和4.35×10-2; 1次方的衰减系数k1=5.16×10-2、8.26×10-2、6.41×10-2和4.53×10-2。
2.2 PDE近场爆轰噪声指向性分析
作为脉冲噪声，PDE近场爆轰噪声主要评价有脉冲声压级和峰值声压级。本文中着重研究峰值声压级，即爆轰噪声声压-时间曲线中声压峰值ppeak的分贝值，表达式为：
L peak =20lg(p peak /p0) (3) 式中：Lpeak为峰值声压级, dB；ppeak为爆轰噪声的峰值声压, Pa；p0=2×10-5 Pa, 为基准声压。
指向性是表示声源在不同的方向辐射声能量的差异性。由图 3可知，通过实验测得三管PDE近场爆轰噪声具有较强的指向性。三管PDE近场爆轰噪声峰值最大值均出现在30°方向。并且随着距离的增加，指向性更加明显。爆轰噪声，近似于高速喷流噪声的一种，主要由冲击波噪声和高速喷流噪声组成，冲击波噪声由爆轰波衰减而成的冲击波组成，高速喷流噪声由高温高压爆轰产物喷出PDE形成的高速喷流产生。文献[5]中对爆轰噪声的频谱计算分析认为，爆轰噪声的声源主要由单极子和四极子源组成。其中的四极子源，即由射流边界层中产生的湍流脉动引起的高频噪声，具有明显的指向性。文献[4]中，测量了单管PDE爆轰噪声指向性，得出了除1倍管径处，其余测量位置处的爆轰噪声辐射最大声压级均在30°方向上的结论，三爆轰管PDE虽不同于单爆轰管PDE，但其声源特性与单爆轰管PDE表现出了相似的规律性。
2.3 PDE噪声近场的时间特性
脉冲噪声的持续时间，也是脉冲噪声重要的评价标准。爆轰波出管口退化而成的冲击波在近场区域仍为较强的冲击波，具有很强的间断性。幅值上升快，下降也快，持续时间较短。本文中采用的判定标准有2种，即A持续时间和B持续时间[9]。按照国家标准[GJB 2A-1996]的定义，A持续时间为噪声在自由场的简单脉冲波，持续时间即指压力上升至主要正峰值，随后又迅速下降至环境压力所需要的时间。对于B持续时间，即在混合场或其他原因产生反射形成的一系列振荡波时，其持续时间为：在声压脉冲波峰值下降90%的声压振幅范围内的时间总和。图 4为0°方向，r=1 000 mm处的声压变化曲线，其中声压峰值为62 kPa, La和Lb分别为波动范围线的上下界限，大小分别为压力峰值ppeak的±1/10。图中O、A两点间的时间差为A持续时间，O、B两点间的时间差为B持续时间。
表 1为0°、30°、60°、90°等4个方向，测试距离分别为600、800、1 000、1 200 mm处的脉冲噪声的持续时间。
表 1 爆轰噪声的持续时间Table 1. Time of duration for detonation noiseφ/(°) r=600 mm r=800 mm r=1 000 mm r=1 200 mm A B A B A B A B 0 0.55 9.64 0.61 10.93 0.63 12.10 0.64 25.56 30 0.45 6.61 0.49 8.14 0.50 9.51 0.57 12.90 60 0.39 7.13 0.41 8.28 0.44 9.16 0.47 14.82 90 0.37 9.16 0.39 12.50 0.40 15.26 0.42 21.91 2.3.1 A持续时间
A持续时间随不同位置、不同方位角的变化情况如图 5(a)所示。在相同的位置r处，随着方位角φ的增加，A持续时间近似线性规律下降。在同一方位角情况下，随着距离r的增大，A持续时间也增大。分析认为，在相同的方位角上，随着轴向距离增大，一定量的脉冲声通过单位面积的声能量不断减小，因而峰压减小，压力-时间曲线拉宽，正脉冲时间也变长。在同一距离r处，由于三爆轰管PDE爆轰噪声的指向性，在30°方向能量辐射比较大，因而不仅压力值高，且A持续时间也长。而0°方向上能量分布较小，但是A持续时间较长，主要是因为三爆轰管虽然是同时点火，但由于三个爆轰管之间交汇流场的复杂性和波系之间的抵消作用，导致到达测试点的时间不一致。图 6为800 mm距离处测量所得压力随时间变化曲线，图中明显可以看出在压力上升区，存在3个峰值的叠加，导致其压力波形的正持续时间变长。
为验证对A持续时间规律分析的正确性，对单爆轰管PDE爆轰噪声近场噪声进行了实验测量。单爆轰管PDE爆轰噪声的最大值在30°方向，A持续时间随着方位角的变化曲线如图 5(b)所示：由图中可以看出，同一方位角下，随着距离的增加，A持续时间不断增加。同一轴向距离处，由于爆轰噪声辐射的指向性，在30°处，A持续时间较长，与上述分析结论一致。
2.3.2 B持续时间
B持续时间随着方位角φ的变化曲线如图 7所示。在600、800、1 000、1 200 mm处，30°和60°的B持续时间均小于同一距离下的0°和90°方向。图 8为800、1 000 mm处的爆轰噪声峰值指向性和B持续时间变化曲线。0°~30°，随着方位角的增加，峰值声压级增加，B持续时间相应减小，在60°~90°区间内，随着方位角的增加，峰值声压级下降，B持续时间增加。这两段区间内，峰值声压级的变化与B持续时间的关系成反比。在30°~60°处，B持续时间与方位角和峰值声压级没有明确的关系。在方位角相同的情况下，随着距离r的增大，B持续时间增加。
图 8 峰值声压级的指向性和B持续时间随方位角的变化曲线Figure 8. Curves of detonation noise directivity and B time duration varying with different angles由上述分析可以看出，B持续时间与噪声峰值具有一定的关系，随着传播距离的增加，峰值逐渐减小，B持续时间增加。图 9为800和1 000 mm处0°方向上压力变化曲线，峰值为84、60 kPa。可以看出，峰值的衰减速度较快，但在小压力扰动区域，衰减速度较慢。3个流场之间的交汇作用较复杂，产生的波系也相对复杂。声场也并不是单管之间的简单叠加，在某些区域存在一定程度的抵消，某些区域存在一定程度的叠加[10]，因此会出现峰值压力减小，B持续时间增大的现象。
图 9 800、1 000 mm处压力波形对比Figure 9. Curves of detonation noise amplitudes varying with time at 800, 1 000 mm3. 结论
通过对三爆轰管脉冲爆轰发动机同时起爆工况下爆轰噪声的研究，得出以下结论：
(1) 爆轰噪声随着传播距离的增加，迅速衰减，在3倍“名义管径”距离之前，按照距离r的负3次方的规律衰减，近场与远场的参考半径在3倍“名义管径”处，3倍“名义管径”之后一定距离处，按照距离r的负一次方的规律衰减。
(2) 爆轰噪声辐射具有明显的指向性，峰值均出现在30°方向。
(3) 在相同的距离r处，随着方位角φ的增大，A持续时间的下降规律近似线性的。在同一方位角情况下，不同距离r处，A持续时间随着r的增大而增加。
(4) B持续时间与声压峰值的大小成反比关系，并且随着距离r的增大，B持续时间增加。在不同的方位角上，峰值声压越大，B持续时间越小。
-
表 1 不同管径和初始压力下五种碳氢混合物爆轰传播模式分类
Table 1. The various evlution modes of the five tested mixtures in different diameter tubes and initial pressures
p0/kPa C2H2+2.5O2+70%Ar C2H2+2.5O2+85%Ar C2H2+5N2O C3H8+5O2 CH4+2O2 1.5 3.2 12.7 1.5 3.2 12.7 1.5 3.2 12.7 1.5 3.2 12.7 1.5 3.2 12.7 98 2, 4 84 1 2 80 1 1 4 60 1 1 1 1 1 1 4 2 57 6 55 1 1 6 1 1 1 2 50 1 1 1 1 1 4, 5 2 40 1 1 1 1 1 1 1 4, 5 4 1 36 1 1 1 1 1 1 4, 5 1 34 1 1 1 2 4, 5 1 32 1 1 1 2 1 4, 5 4 1 30 2 1 1 1 1 2 1 1 2 1 1 6 4 1 29 1 2 2, 4 28 2 2 1 6 1 2 1 1 2, 4 1 1 6 4 1 26 2 2 1 2, 4 1 1 2, 4 1 1 5 1 24 2 1 2, 4 1 1 4 1 1 5 1 22 2 2 1 1 4 1 1 4 1 1 5 1 20 2 2 1 1 4 1 1 1 1 5 2 18 6 2 1 1 4 1 1 1 5 2 16 2 1 1 4 2 1 4 2 1 5 2 15 1 2 6 2 3 14 2 1 1 4 2 1 1 5 3 12 2 1 1 4 2 1 4 1 3 10 2 1 5 4 1 4 1 5 4 8 6 1 5 4 2 4 1 6 4 6 6 2 6 4 2 4 2 6 4 4.5 2 3 4 2 5 2 5 3, 4 4 3 6 4 6 4 6 2 6 4 6 4 6 1 6 6 注：表中管径的单位为mm。 
下载: 导出CSV
-
[1] LEE J H S. The detonation phenomenon[M]. Cambridge:Cambridge University Press, 2008. [2] LEE J J, DUPRE G, KNYSTAUTAS R, et al. Doppler interferometry study of unstable detonations[J]. Shock Waves, 1995, 5:175-181. doi: 10.1007/BF01435525 [3] CAMARGO A, NG H D, CHAO J, et al. Propagation of near-limit gaseous detonations in small diameter tubes[J]. Shock Waves, 2010, 20(6):499-508. doi: 10.1007/s00193-010-0253-3 [4] MOEN I O, SULMISTRAS A, THOMAS G, et al. The influence of cellular regularity on the behaviors of gaseous detonations[J]. Progress in Astronautics and Aeronautics, 1985, 106:220-243. doi: 10.2514/5.9781600865800.0220.0243 [5] LEE J H S, JESUTHASAN A, NG H D. Near limit behavior of the detonation velocity[J]. Proceedings of the Combustion Institute, 2013, 34(2):1957-1963. doi: 10.1016/j.proci.2012.05.036 [6] KITANO S, FUKAO M, SUSA A, et al. Spinning detonation and velocity deficit in small diameter tubes[J]. Proceedings of the Combustion Institute, 2009, 32(2):2355-2362. doi: 10.1016/j.proci.2008.06.119 [7] CAMPBELL C, WOODHEAD D W. The ignition of gases by an explosion wave. Part Ⅰ. Carbon monoxide and hydrogen mixtures[J]. Journal of the Chemical Society, 1926, 129(129):3010-3021. [8] CAMPBELL C, WOODHEAD D W. Striated photographic records of explosion waves[J]. Journal of the Chemical Society, 1927:1572-1578. [9] CAMPBELL C, FINCH A C. Striated photographic records of explosion waves. Part Ⅱ. An explanation of the Strioe[J]. Journal of the Chemical Society, 1928:2094-2106. [10] MANSON N, BROCHET C, BROSSARD J, et al. Vibratory phenomena and instability of self-sustained detonations in gases[J]. Proceedings of the Combustion Institute, 1965, 10:461-469. http://www.sciencedirect.com/science/article/pii/S0082078463800557 [11] EDWARDS D H, HOOPER G, MORGAN J M. A study of unstable detonations using a microwave interferometer[J]. Journal of Physics D:Applied Physics, 1974, 7(2):242-247. doi: 10.1088/0022-3727/7/2/308 [12] HALOUA F, BROULLETTE M, LIENHART V, et al. Characteristics of unstable detonations near extinction limits[J]. Combustion and Flame, 2000, 122(4):422-438. doi: 10.1016/S0010-2180(00)00134-6 [13] MOEN I O, DOATO M, KNYSTAUTUS R, et al. The influence of confinement on the propagation of detonations near the detonability limits[J]. Proceedings of the Combustion Institute, 1981, 18(1):1615-1622. doi: 10.1016/S0082-0784(81)80165-8 [14] MANZHALEI V I. Detonation regimes of gases in capillaries[J]. Combustion, Explosion, and Shock Waves, 1999, 28(3):296-302. doi: 10.1007/BF00749647 [15] MCBRIDE B J, GORDON S. Computer program for calculation of complex chemical equilibrium compositions and applications[R]. User's Manual and Program Description NASA Report, 1996, 19(4):443. 期刊类型引用(6)
1. 赵焕娟，汪乐溪，张英华，林敏，周正青，蒋慧灵. 孔隙比对氢气爆轰波结构的定量影响. 工程热物理学报. 2024(01): 303-309 . 
百度学术2. 周以宁，赵焕娟，徐向宇，林敏，董士铭. 内管扰动对氢气爆轰波传播影响的实验研究. 工程热物理学报. 2022(12): 3402-3413 . 百度学术3. 施伟，关亮，王子模，蒋榕培，徐森. NOFBx推进剂的火焰传播特性试验及分析. 火箭推进. 2021(05): 92-98 . 百度学术4. 韩文虎，张博，王成. 气相爆轰波起爆与传播机理研究进展. 爆炸与冲击. 2021(12): 65-96 . 
本站查看5. 牛淑贞，赵焕娟，张英华，严屹然，秦玄烨. 环管中甲烷-氧气预混气爆轰传播机理研究. 推进技术. 2020(07): 1536-1543 . 百度学术6. 武郁文，褚驰，翁春生，郑权. 孔板扰动对爆轰波胞格结构特性影响的实验研究. 爆炸与冲击. 2019(11): 15-23 . 本站查看其他类型引用(1)
-
下载:
百度学术
计量
- 文章访问数: 5459
- HTML全文浏览量: 1454
- PDF下载量: 38
- 被引次数: 7