| [1] |
郑云, 叶列平, 岳清瑞.CFRP板加固含裂纹受拉钢板的疲劳性能研究[J].工程力学, 2007, 24(6):91-97. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gclx200706016ZHENG Yun, YE Lieping, YUE Qingrui. Study on fatigue behavior of cracked tensile steel plates reinforced with CFRP plates[J]. Engineering Mechanics, 2007, 24(6):91-97. http://industry.wanfangdata.com.cn/dl/Detail/Periodical?id=Periodical_gclx200706016
|
| [2] |
范国玺, 宋玉谱, 王立成.钢筋混凝土框架结构梁柱中节点动态力学性能试验研究[J].振动与冲击, 2015, 34(12):58-64. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zdycj201512011FAN Guoxi, SONG Yupu, WANG Licheng. Experimental study on dynamic mechanical properties of interior RC frame beam-column joints[J]. Journal of Vibration and Shock, 2015, 34(12):58-64. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=zdycj201512011
|
| [3] |
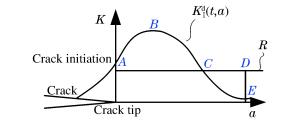
王元清, 周晖, 石永久, 等.基于裂纹扩展阻力曲线的钢结构构件断裂行为评估模型[J].清华大学学报(自然科学版), 2013, 53(5), 595-600. http://mall.cnki.net/magazine/Article/QHXB201305002.htmWANG Yuanqing, ZHOU Hui, SHI Yongjiu, et al. Fracture behavior evaluation model for steel structural components based on crack extension resistance curves[J]. Journal of Tsinghua University (Science & Technology), 2013, 53(5):595-600. http://mall.cnki.net/magazine/Article/QHXB201305002.htm
|
| [4] |
王志华, 赵勇刚, 马宏伟.梁结构中裂纹参数识别方法研究[J].计算力学学报, 2006, 23(3):307-312. https://www.wenkuxiazai.com/doc/4e69730502020740be1e9b4a.htmlWANG Zhihua, ZHAO Yonggang, MA Hongwei. Investigation on crack identification in the beam-type structures[J]. Chinese Journal of Computational Mechanics, 2006, 23(3):307-312. https://www.wenkuxiazai.com/doc/4e69730502020740be1e9b4a.html
|
| [5] |
周晖, 王元清, 石永久, 等.基于微观机理的梁柱节点焊接细节断裂分析[J].工程力学, 2015, 32(5):37-50. http://or.nsfc.gov.cn/bitstream/00001903-5/296412/1/1000014168465.pdfZHOU Hui, WANG Yuanqing, SHI Yongjiu, et al. Fracture analysis of welded details in beam-to-column connections using macromechanics-based models[J]. Engineering Mechanics, 2015, 32(5):37-50. http://or.nsfc.gov.cn/bitstream/00001903-5/296412/1/1000014168465.pdf
|
| [6] |
RUAN H H, YU T X. Deformation mechanism and defect sensitivity of notched free-free beam and cantilever beam under impact[J]. International Journal of Impact Engineering, 2003, 28(1):33-63. doi: 10.1016/S0734-743X(02)00024-6
|
| [7] |
LIU J, ZHU W D, CHARALAMBIDES P G, et al. A dynamic model of a cantilever beam with a closed, embedded horizontal crack including local flexibilities at crack tips[J]. Journal of Sound and Vibration, 2016, 382:274-290. doi: 10.1016/j.jsv.2016.04.036
|
| [8] |
MANOGG P. International conference on the physics of non-crystalline solids[M]. Netherlands, 1964:481-490.
|
| [9] |
THEOCARIS P S, PAPADOUPOUS G A. The influence of geometry of edge-cracked plates on KⅠ and KⅡ components of the stress intensity factor studied by caustics[J]. Journal of Physics D:Applied Physics, 1984, 17(12):2339-2349. doi: 10.1088/0022-3727/17/12/003
|
| [10] |
YAO X F, JIN G C, ARAKAWA K, et al. Experimental studies on dynamic fracture behavior of thin plates with parallel single edge cracks[J]. Polymer Testing, 2002, 21(8):933-940. doi: 10.1016/S0142-9418(02)00037-5
|
| [11] |
YANG R S, XU P, YUE Z W, et al. Dynamic fracture analysis of crack-defect interaction for mode I running crack using digital dynamic caustic method[J]. Engineering Fracture Mechanics, 2016, 161:63-75. doi: 10.1016/j.engfracmech.2016.04.042
|
| [12] |
李清, 刘绍兴, 苏鹏, 等.预制裂纹梁柱节点冲击破坏过程的动态焦散线实验研究[J].振动与冲击, 2008, 27(10):23-26. doi: 10.3969/j.issn.1000-3835.2008.10.006LI Qing, LIU Shaoxing, SU Peng, et al. Experimental study on impactive fracture behavior of a beam-column connection with cracks by caustic method[J]. Journal of Vibration and Shock, 2008, 27(10):23-26. doi: 10.3969/j.issn.1000-3835.2008.10.006
|
| [13] |
王综秩, 王元清, 杜新喜, 等.有机玻璃与不锈钢连接节点承载性能试验研究[J].东南大学学报(自然科学版), 2016, 46(1):105-109. doi: 10.3969/j.issn.1001-0505.2016.01.018WANG Zongzhi, WANG Yuanqing, DU Xinxi, et al. Experimental research on bearing capacity of joint of acrylic and stainless steel[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(1):105-109. doi: 10.3969/j.issn.1001-0505.2016.01.018
|
| [14] |
黄川腾. 空心楼盖结构分析方法及板柱节点冲切问题研究[D]. 重庆: 重庆大学, 2015: 41-48. http://cdmd.cnki.com.cn/Article/CDMD-10611-1016704798.htm
|
| [15] |
赵秋, 陈宝春, 郭智勇, 等.新月形拱-连续梁组合桥梁结构体系试验研究[J].土木工程学报, 2015, 48(增刊1):8-14. http://www.cnki.com.cn/Article/CJFDTotal-TMGC2015S1003.htmZHAO Qiu, CHEN Baochun, GUO Zhiyong, et al. Experimental studies on crescent arch-continuous beam composite bridge structures[J]. China Civil Engineering Journal, 2015, 48(suppl 1):8-14. http://www.cnki.com.cn/Article/CJFDTotal-TMGC2015S1003.htm
|
| [16] |
BEINERT J, KALTHOFF J F. Experimental determination of dynamic stress intensity factors by shadow patterns[M]. Netherlands:Springer, 1981:281-330.
|
| [17] |
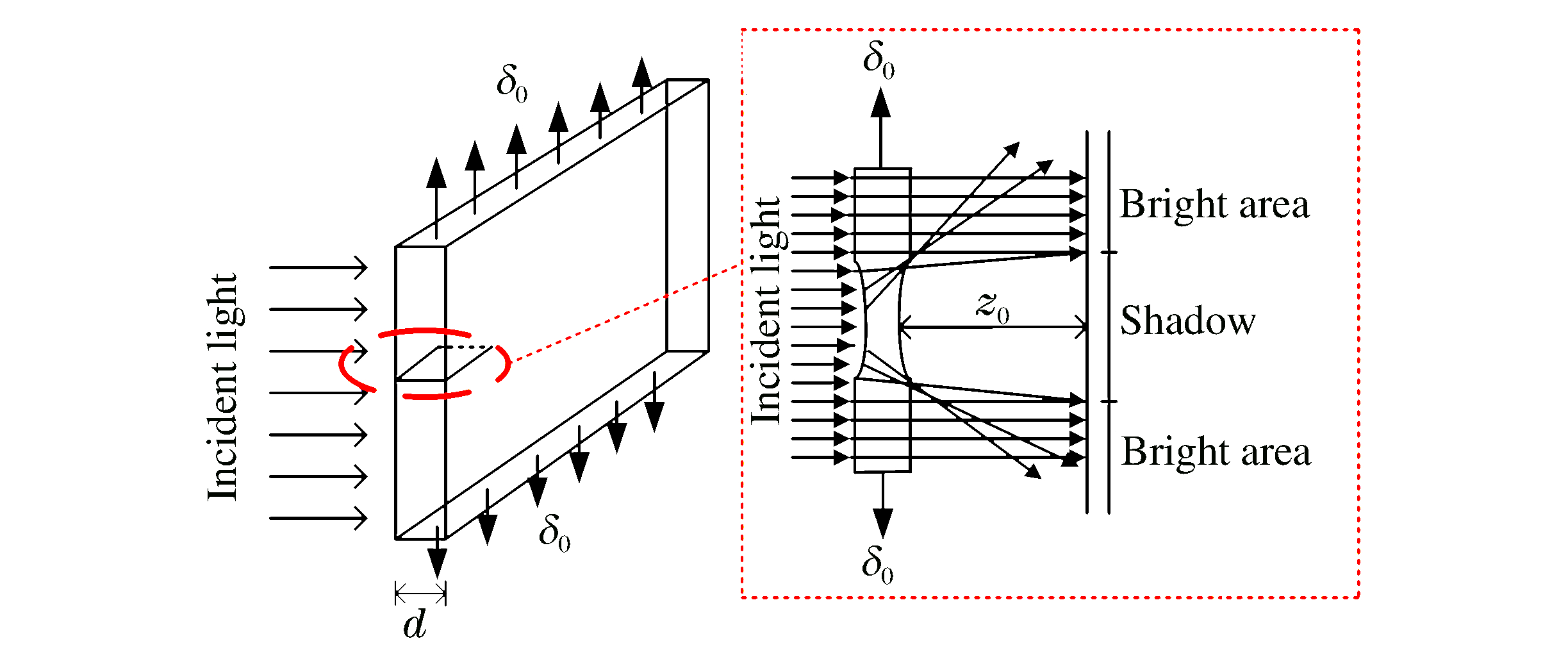
KALTHOFF J F. Shadow optical method of caustics[M]//Handbook on Experimental Mechanics. New York:Prentice Hall, 1987:430-500.
|
| [18] |
TAKAHASHI K, ARAKAWA K. Dependence of crack acceleration on the dynamic stress-intensity factor in polymers[J]. Experimental Mechanics, 1987, 27(2):195-200. doi: 10.1007/BF02319474
|
| [19] |
ZHANG Q B. A review of dynamic experimental techniques and mechanical behavior of rock materials[J]. Rock Mechanics and Rock Engineering, 2014, 47(4):1411-1478. doi: 10.1007/s00603-013-0463-y
|
| [20] |
BROKE D. Elementary engineering fracture mechanics[M]. Martinus Nijho Publishers, 1982:154-156.
|






 下载:
下载: