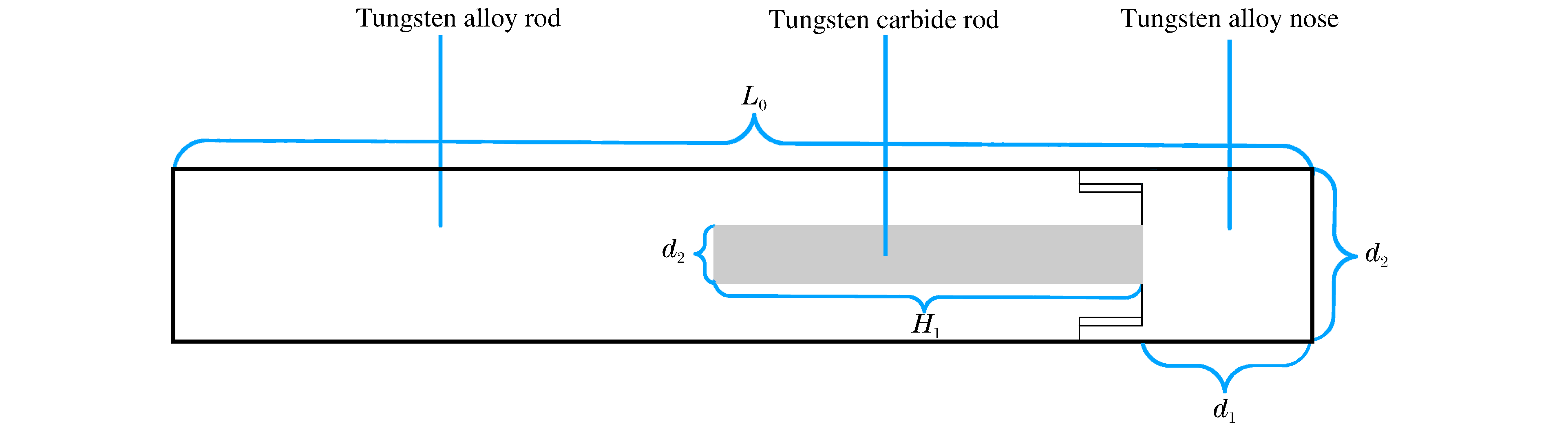
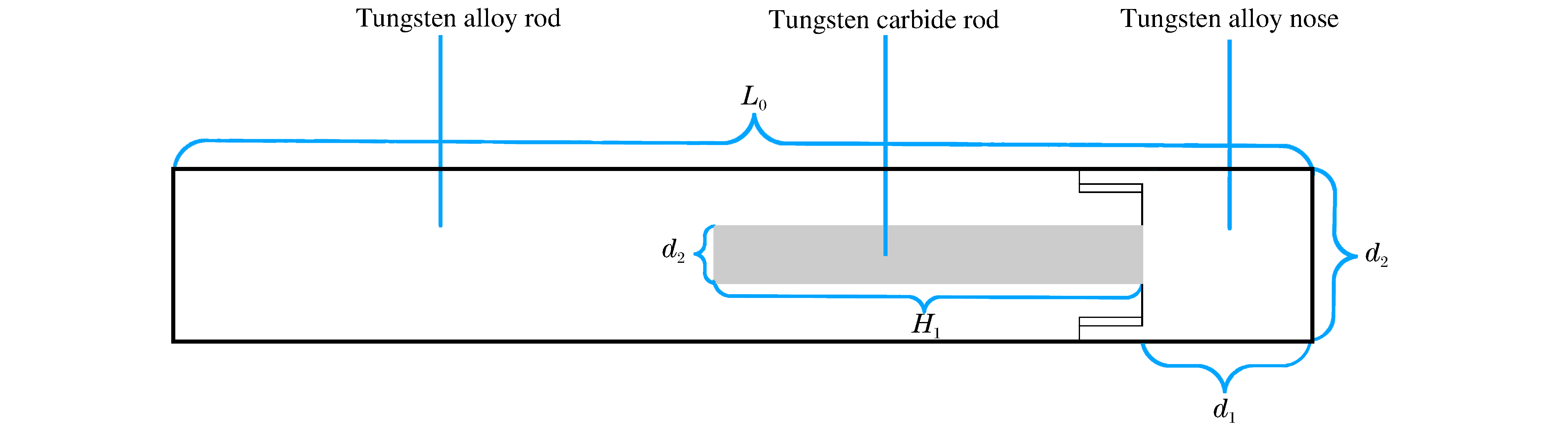
Simplified model of pre-composited rod's normal penetration into steel target
-
摘要: 针对均质长杆体侵彻能力提高陷入瓶颈的问题,设计了由高密度钨合金和高硬度碳化钨组合的新型前置组合杆体。通过试验和数值模拟验证,前置组合杆体能利用材料的不同性能,在稳定侵彻阶段形成更尖锐头部形状,从而提高侵彻能力。根据试验和数值模拟结果,描述了前置组合杆体垂直侵彻钢靶的物理图像,将前置组合杆体侵彻划分为开坑段、组杆段和单杆段三部分,分别建立其各自侵彻阶段的理论模型,最终得到前置组合杆体总侵彻深度计算模型。通过与试验和数值模拟结果对比,验证了该模型的合理性。Abstract: In this study, to improve the penetration capability of the homogeneous long rod, a problem whose solution has hit a bottleneck, we designed a new pre-composited rod fabricated with high density tungsten alloy and high hardness tungsten carbide. It was validated through experiment and numerical simulation that our newly-designed rod can form a sharp nose shape in the steady penetration stage by cashing in on the different properties of different materials to improve the penetration capability of the long rod. Based on the experimental and simulated results, we presented a full description of the physical image of the pre-composited rod's normal penetration into a steel target, which can be divided into three sections, those of the cratering, the composited rod, and the homogeneous rod, with their theoretical models established respectively, thus obtaining the calculation model of the total pre-composited rod's penetration depth. The rationality of the model was verified by comparing it with the experiment and simulation results. The conclusions from our study are helpful for the kinetic design of weapons using the new long rod.
-
刚性弹侵彻混凝土研究中,弹体初始头部形状对侵彻能力具有非常明显的影响,弹体头形系数越小,所受靶体阻力越小,侵彻威力越高。Forrestal等[1]、Rosenberg等[2]、Jones等[3-4]、陈小伟等[5]、李庆明等[6]和Chian等[7]都对不同头形的刚性弹丸侵彻混凝土靶进行过研究,得到了不同头形的弹体所受的靶体阻力计算公式,并分析了不同头形系数对侵彻威力的影响。
长杆体侵彻钢靶研究中,通常认为杆体初始头部形状对长杆体侵彻威力影响不大,因为在高速侵彻中长杆体侵彻的特点是杆体边破碎边侵彻。程兴旺等[8]和高光发等[9]对长杆体初始头部形状对侵彻的影响进行了数值模拟,研究表明高速侵彻中长杆体初始头部形状对侵彻影响不大。但更进一步研究长杆体侵彻钢靶中发现,不同材料由于其侵彻机理不同,在稳定侵彻过程中其破碎头部形状是不同的,如贫铀合金杆体和钨合金杆体。在着靶速度1.2~1.9 km/s范围内,贫铀合金杆体与相近密度的钨合金杆体相比,其侵彻效率要高出10%以上[8]。两者侵彻性能出现差异的原因是贫铀合金其临界绝热剪切应变率较低,易发生绝热剪切破坏,故在侵彻过程中其头部不断被削尖,产生“自动锐化”现象,破碎头部呈圆锥形;钨合金的临界绝热剪切应变率较高,在侵彻过程中其破碎头部呈蘑菇头形。由此可见,稳定侵彻过程中杆体头部形状对侵彻威力影响很大。
综上,为了突破均质长杆体侵彻瓶颈,本文中采用高密度的钨合金和高硬度的碳化钨两种材料进行结构组合,设计了一种前置组合杆体结构,以期能够利用两种材料发生侵蚀的先后顺序不同,从而在稳定侵彻过程中形成较钨合金均质杆体更尖锐的头部,用组合结构形成杆体头部锐化效果(即结构自锐),提高侵彻威力。
1. 验证试验和数值模拟
1.1 验证试验
采用钨合金和碳化钨两种材料进行结构组合设计了图 1所示的前置组合杆体结构,其中实体部分为钨合金头部和钨合金杆体,两者采用螺纹联接,阴影部分为碳化钨前置小杆体,与钨合金杆体采用过盈配合。加工钨合金头部主要有2个作用:一方面是防止碳化钨杆体从前端脱落,起固定作用;另一方面是用于弹靶刚接触时开坑的消耗,使碳化钨杆体在稳定侵彻阶段开始发挥作用。
钨合金杆体总长度L0为100 mm,杆体直径d1为10 mm,长径比为10,共加工了4组杆体,方案如表 1所示。靶体选用45钢圆锭,直径为120 mm,厚度为120 mm。
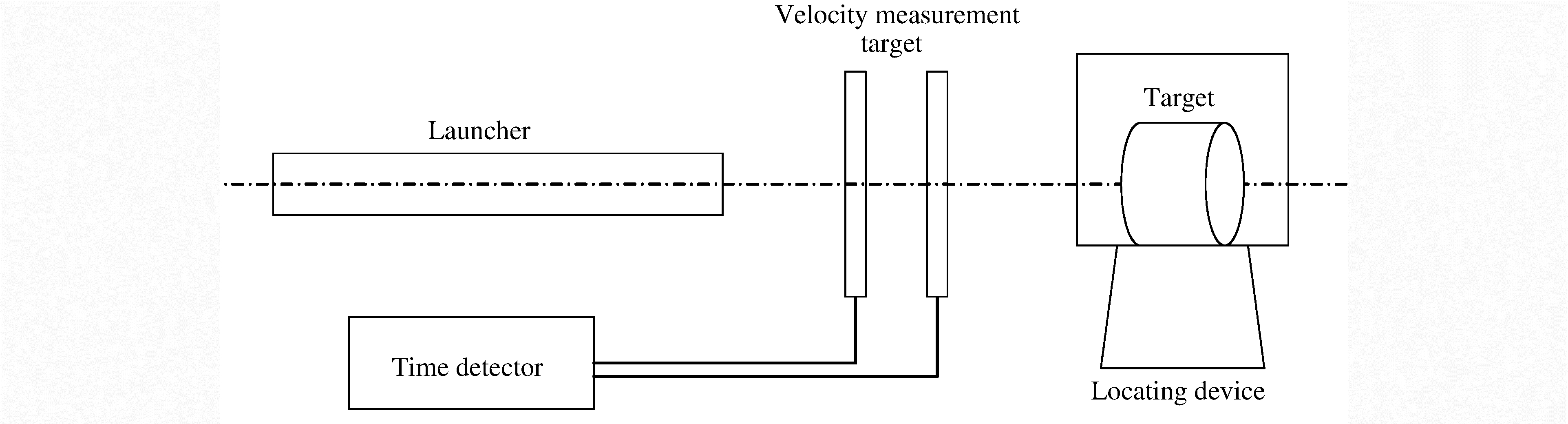
表 1 不同配置的前置组合杆体Table 1. Different configurations of pre-composited rods杆结构 小杆体直径d2/mm 小杆体长度H1/mm 均质杆 0 0 前置组合杆体1 1.5 25 前置组合杆体2 2.5 30 前置组合杆体3 5.5 30 采用25 mm口径的滑膛炮进行发射弹体,试验布置如图 2所示。
将4组杆体进行了对比试验,得到了图 3所示的结果。
由图 3可以看出,杆体入射角度都很正,可作为杆体垂直侵彻钢靶分析研究的依据。具体试验结果将结合数值模拟结果一起分析。
1.2 试验工况的数值模拟
按试验工况,采用AUTODYN_2D软件建立了前置组合杆体垂直侵彻钢靶的有限元模型,如图 4所示。钨合金杆体和碳化钨前置小杆体采用固连接触,杆体网格尺寸为0.25mm,靶体网格采用中间密两边疏的设置,中间密集部分网格尺寸也为0.25mm。靶体的两侧采用非反射边界。弹靶材料都采用Johnson-Cook本构模型,所涉及的主要材料参数见表 2。表 2中ρ为材料密度,G为剪切模量,σy为屈服强度,γ为Grüneisen系数。
表 2 不同配置的前置组合杆体Table 2. Different configurations of pre-composited rods材料 ρ/(g·cm-3) G/GPa σy/MPa γ 93钨 17.6 136 1 506 1.54 碳化钨 14.7 254 5 100 1.50 45钢 7.85 77 700 2.17 1.3 试验和数值模拟结果对比
将4组杆体的数值模拟结果与试验数据进行了比较,得到结果如表 3所示,h为总侵彻深度。由于碳化钨密度小于钨合金,前置组合杆体的初始质量均低于钨合金均质杆体。在此前提下,试验结果显示,在着靶速度低于钨合金均质杆体的情况下,前置组合杆体的侵彻深度与后者相近,这说明前置组合杆体侵彻能力优于相同外形结构的钨合金均质杆体。
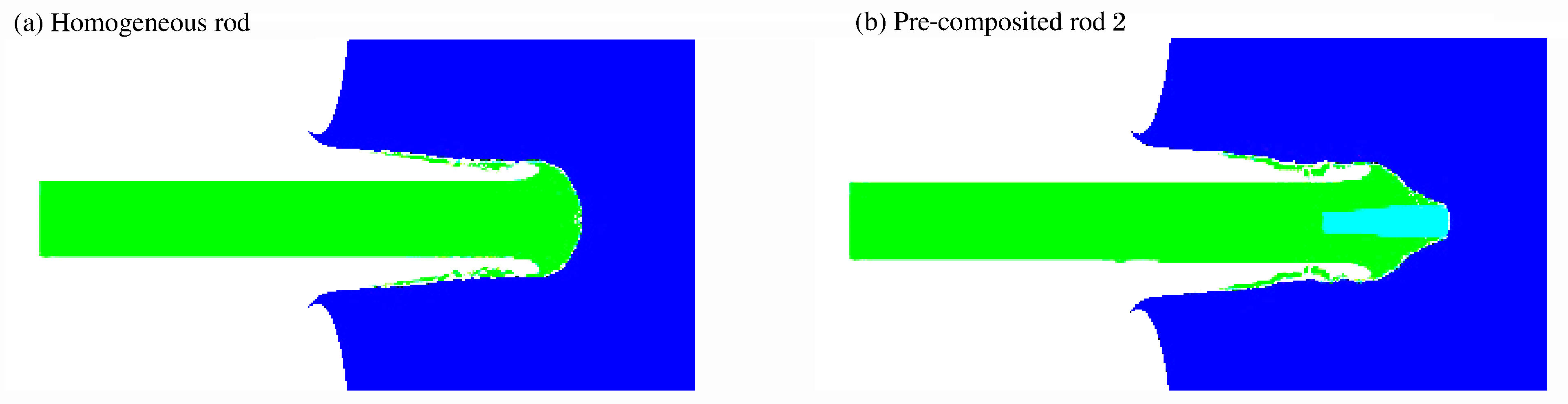
表 3 两组杆体头部形状图Table 3. Nose shape of two rods杆结构 v/(m·s-1) h/mm ε/% 试验 数值模拟 均质杆 1 356 84.0 81.5 2.98 前置组合杆体1 1 310 83.0 77.7 6.39 前置组合杆体2 1 320 84.0 80.9 3.70 前置组合杆体3 1 200 78.0 76.2 2.31 由相对误差的比较可以看出,数值模拟结果与试验结果的相对误差在10%以内,这说明数值模拟符合试验,可用于进一步前置组合杆体侵彻机理分析。数值模拟结果体现了与试验相同的规律,前置组合杆体2在杆体质量和着靶速度都低于钨合金均质杆体的情况下,其侵彻深度接近后者,再次证明了前置组合杆体能够提高侵彻能力。通过观察图 5所示的均质杆和前置组合杆体2这两组杆体在侵彻过程中的图片,可以发现钨合金均质杆体侵彻头部形状呈蘑菇头形,而前置组合杆体呈截锥形,这就是前置组合杆体侵彻能力优于相同外形结构的钨合金均质杆体的原因。
数值模拟的头部形状比较分析中可以看出,前置组合杆体能够提高侵彻能力的原因是碳化钨具有高强度高硬度,在组合杆体侵彻阶段外围的钨合金杆体首先被侵蚀完,此时碳化钨小杆体还未被侵蚀完,中心的碳化钨小杆体率先参与接下来的侵彻,使组合杆体头部形状较钨合金均质杆体更尖锐,形成了结构自锐效果,减小了杆体所受的靶体阻力,从而提高了杆体的整体侵彻威力。
1.4 数值模拟规律分析
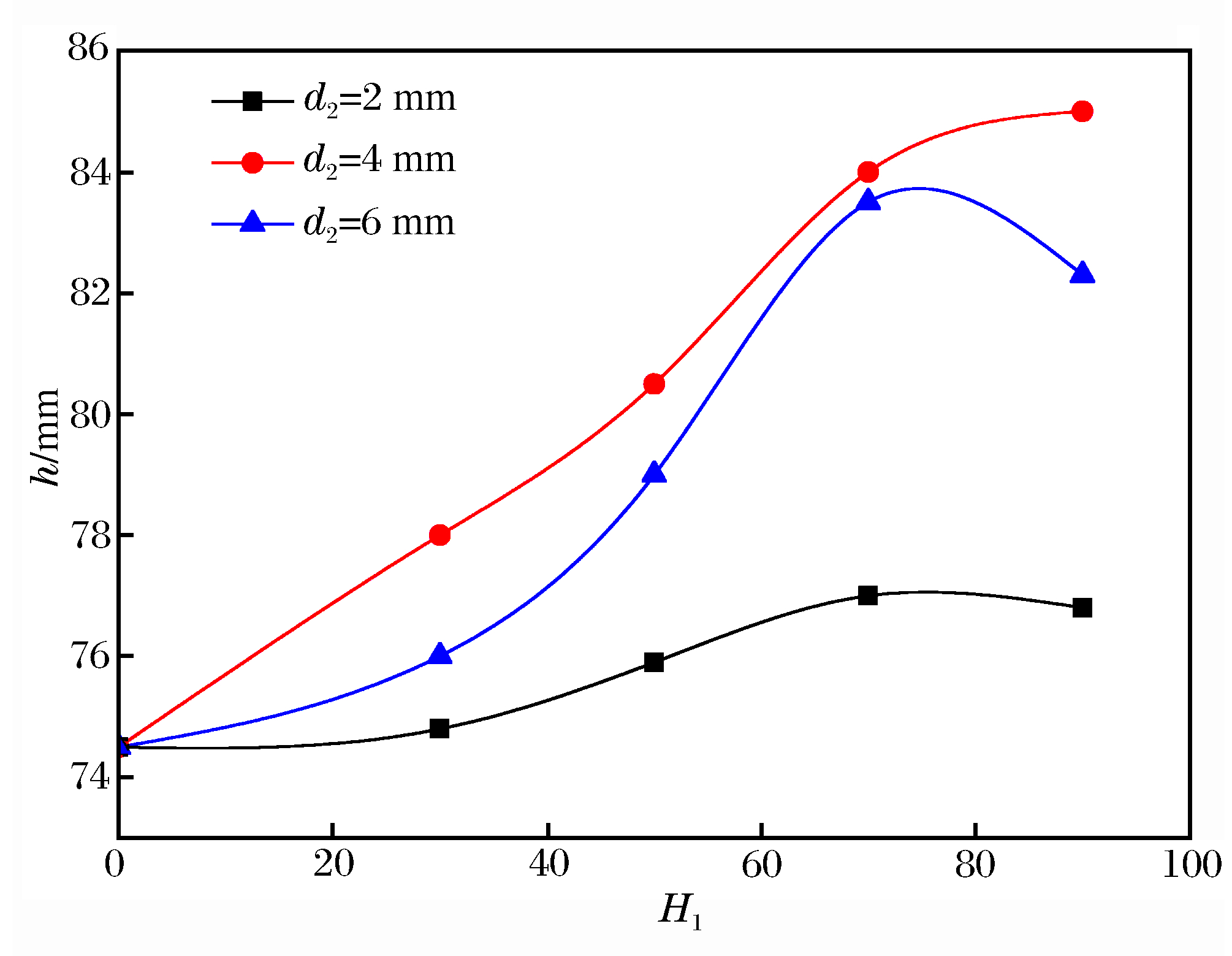
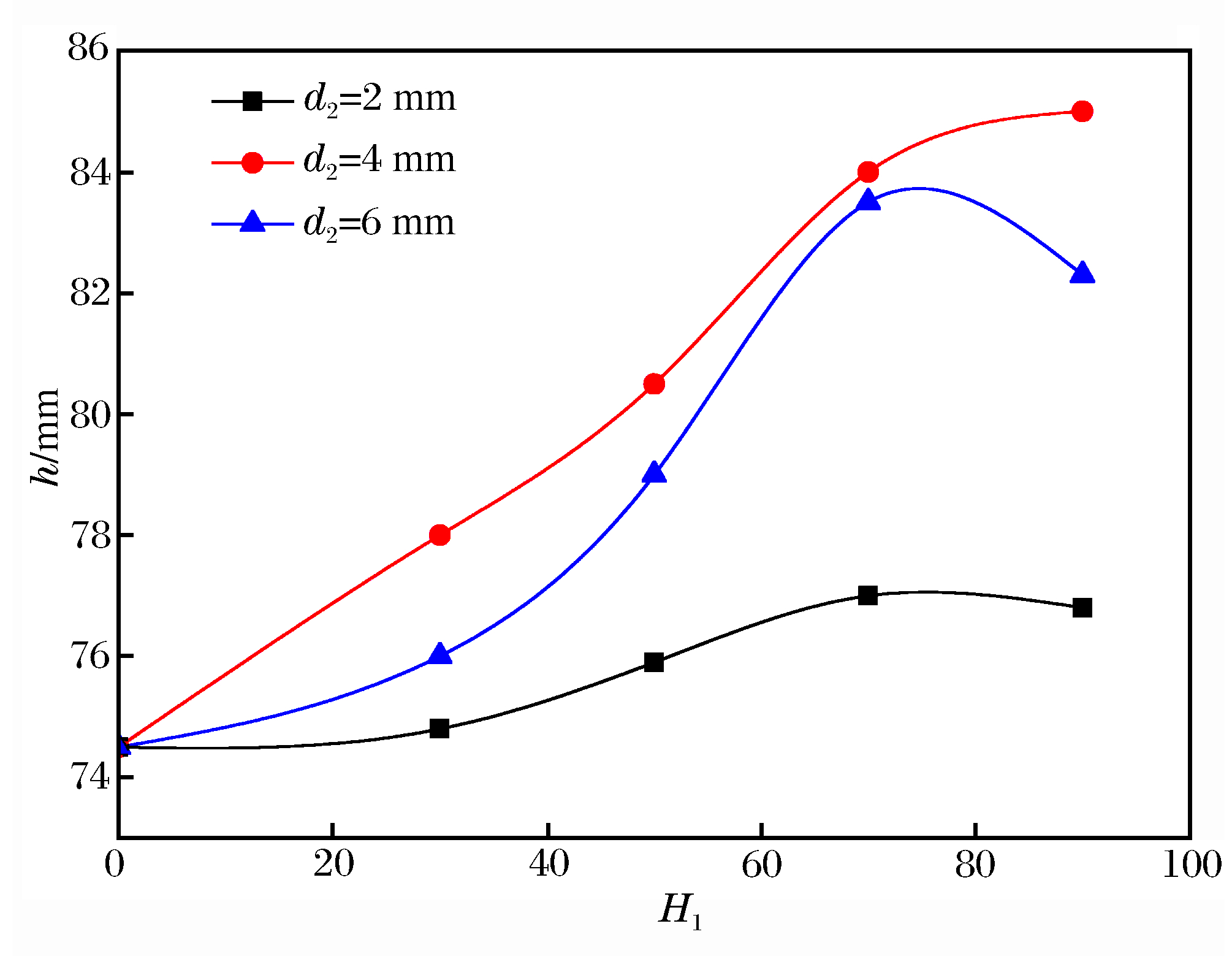
在分析前置组合杆体提高侵彻能力的基础上,接下来对不同配置的前置碳化钨小杆体的前置组合杆体进行数值模拟规律分析。选择2、4和6 mm三种直径,30、50、70和90 mm四种长度共12种配比的前置组合杆体与钨合金均质杆体在着靶速度段1 300 m/s进行数值模拟,得到了不同配置的前置组合杆体的侵彻深度,如图 6所示。
当着靶速度为1 300 m/s时,前置组合杆体的侵彻深度都高于钨合金均质杆体,其侵彻能力都优于后者。从不同直径比较可以看出,碳化钨杆体直径4 mm的前置组合杆体侵彻深度最大,直径6 mm的次之,直径2 mm的最小。碳化钨杆体直径6 mm的前置组合杆体侵彻深度小于直径4 mm的,这是由于碳化钨密度小于钨合金,前者质量小于后者,两者初始动能相差较大,导致了前者侵彻深度低于后者。但碳化钨杆体直径6 mm的前置组合杆体侵彻深度大于均质杆体和直径2 mm的,说明在此着靶速度直径6 mm的碳化钨小杆体仍在发挥着其材料性能上的优势。
从相同直径不同长度比较来看,三种直径碳化钨杆体的前置组合杆体侵彻深度总体上仍随小杆体长度增加而增加。只有碳化钨杆体直径6 mm的前置组合杆体在小杆体长度从70 mm增加至90 mm时出现下降,其原因是随着质量下降,初始动能降低。
2. 模型建立
2.1 侵彻过程描述
前置组合杆体垂直侵彻钢靶的过程,通过数值模拟观察,大致可分为以下开坑、组杆侵彻和单杆侵彻3个阶段。
前置组合杆体侵彻钢靶时,由于靶体材料的塑性流动和飞溅,在靶体表面形成弹坑,此即为侵彻初期的开坑阶段。为了简化计算,假定杆体侵彻后减小1倍弹径时开坑阶段结束。开坑结束后,钨合金杆体和前置碳化钨小杆体组合段侵彻。作用在组合杆体头部的应力达到一定程度时会造成杆体材料的破坏,由于碳化钨硬度和强度高于钨合金,故钨合金管体在外侧首先被侵蚀,碳化钨杆体被侵蚀速度较慢,加上碎渣反向流动的共同作用,形成了较尖锐的杆体头部形状,破碎的杆体材料在弹孔内沿弹杆周围反向排出。随着杆体继续向靶体侵彻,组合杆体的长度不断缩短,速度不断降低,直到组合杆体段被侵蚀完。组合杆体段侵彻结束后,后端的钨合金杆体段继续侵彻靶体,此侵彻过程即为单杆侵彻过程。此阶段靶体材料继续受压引起塑性流动,弹孔继续加深,钨合金杆体受到靶体阻力而变形破坏,形成蘑菇头形状杆体头部。随着侵彻,杆体长度继续缩短,速度继续降低,但钨合金杆体以此稳定阶段破碎杆体头部形状继续向靶内推进,直到侵彻速度为零,侵彻完全停止。
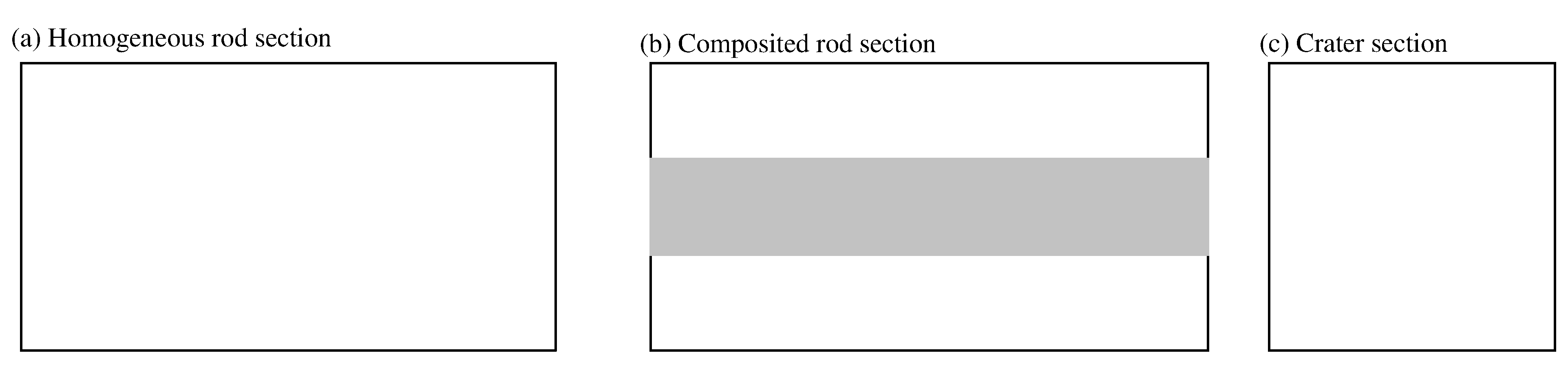
根据前置组合杆体垂直侵彻钢靶侵彻过程的描述,在理论计算中划分成图 7所示的三段,三段杆体侵彻深度之和即为前置组合杆体总的侵彻深度。
2.2 基本假设
前置组合杆体垂直侵彻钢靶的主要特点与均质杆体侵彻基本相同,都是杆体在侵彻过程中本身不断地破坏消耗,但存在一个区别是前置组合杆体侵彻时存在一个组杆段的侵彻,此时钨合金管体和碳化钨杆体共同作用到靶体参与侵彻。为了对侵彻过程建立一个简化的数学模型,作如下的基本假设:
(1) 前置组合杆体垂直侵彻钢靶的过程可作为一维准定常运动考虑,即在运动中的物理量随时间变化比较缓慢,在某一时刻前后,运动的物理图像基本相同。
(2) 弹体和靶体密度为常数,不随变形、破碎和硬化等状态变化而改变。
(3) 假定弹坑直径为常数,其值为杆体直径的两倍。试验结果观察到弹坑直径都为约20 mm,故在理论计算中为简化计算,将其取常值。
(4) 假定组杆段和单杆段侵彻过程中其破碎头部形状保持不变,可通过积分求杆体所受靶体阻力。
(5) 忽略开坑段至组杆段以及组杆段至单杆段间的头部形状变化的过渡。
(6) 忽略弹靶摩擦阻力的影响。
2.3 方程建立
按照图 7的划分,分别对开坑段、组杆段和单杆段建立计算方程,将上一阶段的计算结果作为下一阶段的初始条件,最终求得前置组合杆体总的侵彻深度。
2.3.1 开坑段
开坑阶段参照孙庚辰等[10]的长杆弹垂直侵彻半无限靶的简化模型进行计算。
杆体侵彻靶体时,杆体向前运动时受到排开靶体材料的抗力p,由两部分组成,即p=ps+pi。ps为静抗力,pi为动抗力,其表达式为:
ps=23Yt(1+ln2E3Yt)+2π227Et=Rt (1) pi=ρt(D2dudt+32u2) (2) 坑底压力可简化为:
p=Rt+ρt(D2dudt+32u2) (3) 式中:Yt为靶板材料的屈服强度,E为靶板材料的杨氏模量,Et为靶材的硬化模量,ρt为密度,u为弹坑底运动速度,即侵彻速度;D为弹坑直径。
在开坑阶段初期,杆体碰击靶体的时刻,靶体对于杆体侵入的静抗力ps相当于静态冲孔时施加于材料表面的压力,等于材料的硬度HB。本文模型中假设杆体长度消耗到1倍弹径时,开坑段结束,此时静抗力达到式(1)表示的值Rt。假设在开坑阶段内静抗力是连续过渡的,设:
ps=c1e(L0−l)/D+c2,L0−d1≤l≤L0 (4) 式中:L0为杆体初始长度,d1为杆体直径,l为杆体即时长度。
由初始条件l=L0时ps=HB,最终条件l=L0-d1时ps=Rt,得到:
c1=Rt−HBe−1c2=eHB−Rte−1 (5) 在开坑初期,假定坑底压力作用面积A与弹体横截面积A0相同,A=A0=πd124。
由试验得弹坑直径均约为20 mm,即杆体直径d1的2倍,故开坑结束时,坑底直径D取为2d1,即坑底面积A=4A0。
开坑过程中,A=π[d1+(L0−l)]24。开坑段杆长的变化方程为:
dldt=−(v−u) (6) 未变形部分的前置组合杆体的运动方程为:
{14πρ1d21(l−H1)+14π[ρ1(d21−d22)+ρ2d22]H1}dvdt=−14πd21Y1 (7) 式中:ρ1为钨合金密度,ρ2为碳化钨密度,Y1为钨合金的动态屈服强度,两边同时除以杆体面积,经简化,式(7)变为:
[ρ1l−(ρ1−ρ2)H1d22d21]dvdt=−Y1 (8) 开坑段坑底弹渣的运动方程参照文献[10]为:
Y1+2ρ1(v−u)2=Ap/A0 (9) 开坑段侵彻深度方程为:
dxdt=u (10) 初始侵彻速度u0可通过式(9)和初始条件求得。
结合以上方程以及初始条件t=0时l=L0,v=v0,u=u0,x=0,终止条件l=L0-d1,即可求得开坑段结束时的杆体速度v1和侵彻深度x1,将这些计算结果作为下一阶段侵彻的初始条件。
2.3.2 组杆段
组合杆体段是钨合金管体和碳化钨杆体两部分共同作用,涉及的杆体的长度变化和运动变化与单杆侵彻不同,需要作进一步地具体分析。
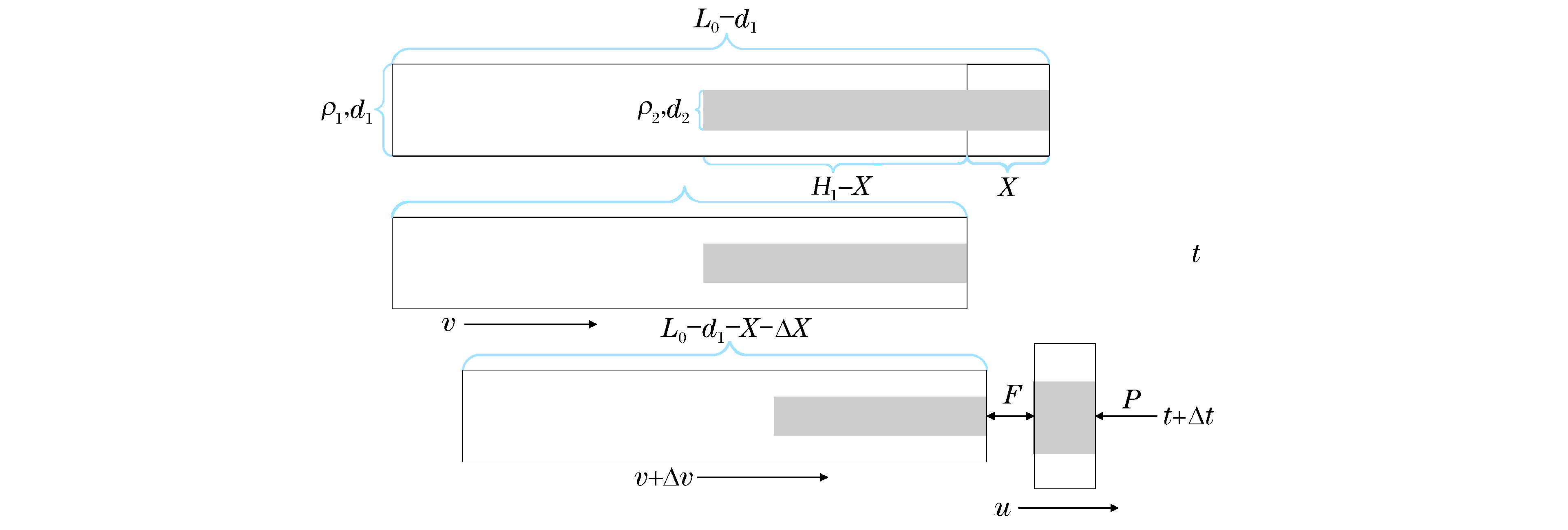
通过观察数值模拟中前置组合杆体的侵彻过程发现组杆段在侵彻过程中其破碎头部形状基本保持不变,在前文中也作了组合段侵彻杆体头部形状不变的假设,故组合杆体段侵彻时杆体所受的靶体阻力P可参考文献[11]求得。组合杆体侵彻过程中对应的头部形状的几何函数y=y(x)由对应方案的组合杆体数值模拟观察得到。组合杆体段的运动变化见图 8。
由图 8可知,在t时刻,长度为X的组合段杆体已被侵蚀掉,剩余杆体长度为L0-d1-X,以速度v运动,此时杆体的动量为:
p|t=14π{[ρ1(d12−d22)+ρ2d22](H1−X)+ρ1d12(L0−d1−H1)}v (11) 下一瞬间,在t+Δt时刻,一部分杆发生了塑性变形,剩余保持不变的杆体速度变化Δv,此时杆体的动量为:
p|t+Δt=14π{[ρ1(d12−d22)+ρ2d22](H1−X−ΔX)+ρ1d12(L0−d1−H1)}(v+Δv)+14π[ρ1(d12−d22)+ρ2d22]ΔXu (12) 从t至t+Δt,由于内力F大小相等、方向相反,只有外力P在作用,其方向与运动方向相反,所以冲量为:
I=−PΔt (13) 在Δt的变化时间内,组合段杆体的运动满足一维的动量守恒,由动量改变等于冲量,得:
I=p|t+Δt−p|t (14) 将式(11)、(12)和(13)代入式(14),并两边同时除以Δt,Δt向0取极限,得:
−P=14π{[ρ1(d12−d22)+ρ2d22](H1+d1−L0+l)+ρ1d12(L0−d1−H1)}˙v+14π[ρ1(d12−d22)+ρ2d22](v−u)˙l (15) 未变形部分杆体的减速方程,两边同时除以14π,为:
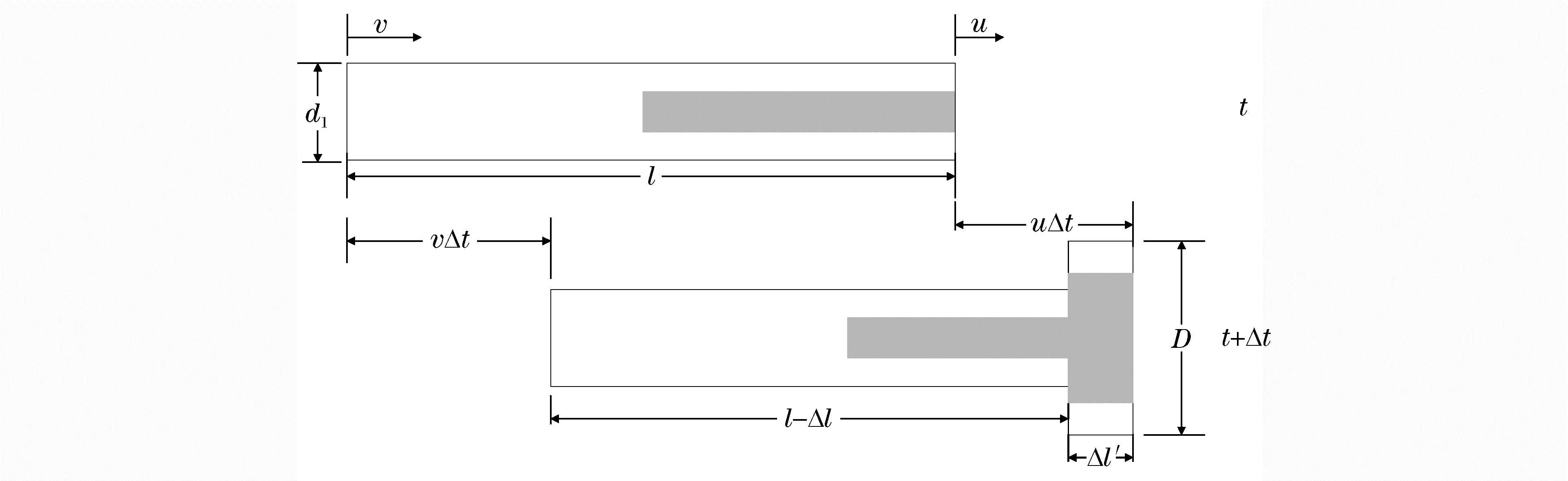
{[ρ1(d12−d22)+ρ2d22](H1+d1−L0+l)+ρ1d12(L0−d1−H1)}dvdt=−(d12−d22)Y1−d22Y2 (16) 前置组合杆体组合段的杆长变化如图 9所示。
由图中可知,从t至t+Δt,长度为Δl的组合杆体发生了塑性变形,未变形前的杆体直径为d1,变形后的杆体直径为D,由于假设侵彻过程中杆体的密度不发生变化,故变形后的杆体长度Δl'为:
Δl′=d21D2Δl (17) 从图 9可以看出,变形前的杆体长度与杆体前端运动位移之和一定等于杆体末段运动位移与变形后的杆体长度之和,故:
l+uΔt=vΔt+(l−Δl)+Δl′ (18) 将式(17)代入式(18),并两边同时除以Δt且Δt向0取极限,得:
(d21D2−1)dldt=v−u (19) 结合式(15)~(16)、(19)以及侵彻深度变化式(10),初始条件为l=L0-d1,终止条件为l=L0-d1-H1,再代入开坑段结束求得的杆体速度v1即可求得组合杆体段结束时的杆体速度v2和侵彻深度x2,将这些计算结果作为下一阶段单杆段侵彻的初始条件。
2.3.3 单杆段
单杆段的计算参照文献[11],数值模拟观察到单杆段侵彻过程中其杆体头部形状基本保持蘑菇头形,通过积分求得单杆段杆体所受的靶体阻力P。
单杆段杆体的动量守恒关系式为:
−P=14πρ1d12[l˙v+˙l(v−u)] (20) 单杆段的减速方程为:
ρ1l˙v=−Y1 (21) 因假设整个侵彻过程中,弹坑直径不变,故单杆段杆体长度变化方程与组杆段相同,也为式(19)。
当前置组合杆体侵彻到单杆段时,其初始条件为l=L0-d1-H1和杆体速度v2,当侵彻速度降为v3=0时,侵彻停止。可结合式(19)~(21)以及侵彻深度变化式(10)利用上述初始和终止条件求得单杆段侵彻深度x3。
前置组合杆体总的侵彻深度x即为三段侵彻深度之和:
x=x1+x2+x3 (22) 3. 模型验证
对试验工况使用建立的前置组合杆体垂直侵彻钢靶模型计算,计算中所涉及的弹靶材料为45钢,其主要参数为:HB=180 kg/mm2,静抗力Rt=5 077 MPa,硬化模量Et=3 724 MPa。
首先对前置组合杆体1在着靶速度1 310 m/s垂直侵彻钢靶进行理论计算,采用龙格-库塔法对开坑阶段的常微分方程组进行求解,当杆体长度l减少1倍杆体直径时,计算停止,得到的杆体速度v1为1 295.5 m/s,侵彻深度x1为10.9 mm。
由于杆体长度消耗为1倍杆体直径即开坑结束以及忽略开坑段至组杆段头部形状变化过渡的假设,开坑段结束即进入组杆段稳定侵彻阶段,可直接利用组杆段公式求解。首先需要获得组杆段所受的靶体阻力P,由组杆段稳定侵彻过程中其破碎头部形状保持不变的假设,可通过观察数值模拟中组合杆体头部形状来获得杆体的头形系数M和N,从而得到靶体阻力P关于侵彻速度u的表达式。
前置组合杆体1的组杆段侵彻时头部形状如图 10所示。由图 10可知,此前置组合杆体稳定侵彻的头部形状类似截锥形,故将前置组合杆体组杆段稳定侵彻的头部形状假定为如图 11所示的截锥形。
截锥形头部所受阻力由平头部分所受阻力P1和锥形部分所受阻力P2两部分组成:
P=P1+P2 (23) 平头部分所受阻力P1为:
P1=πD214(AYtM1+Bρtu2N1) (24) 式中:M1和N1为头形系数,对于平头杆体,两者均等于1。
锥形部分所受阻力P2为:
P2=π(D2−D12)4(AYtM2+Bρtu2N2) (25) 锥形部分头部母线的几何函数为:
y=−D−D12bx+D2 (26) 将式(26)代入文献[11]中已知y=y(x)的头型系数M和N的表达式,并忽略摩擦阻力,即令μ=0,可求得M2=1,N2=−(D1−D)3(D1+D)4b2D2+(D1−D)2D2。
将式(24)和(25)代入式(23),可得:
P=πD24(AYtM+Bρtu2N),M=1,N=D12+(D2−D21)N2D2 (27) 由数值模拟观察到前置组合杆体1的组杆段的头部形状为b=12D,D1=15D,代入式(27),求得N=0.4。
已知M和N,即得到了靶体阻力P关于侵彻速度u的表达式,结合式(15)~(16)、(19)以及侵彻深度变化式(10),初始条件杆长l为90 mm,杆体速度v1为1 295.5 m/s,终止条件为l=65 mm,可求得组杆段侵彻结束时杆体速度v2为1 257.9 m/s,侵彻深度x2为22 mm。
随着前置组合杆体进入后段单杆侵彻时,此时杆体头部形状如图 12所示。由图 12可知,前置组合杆体的后段单杆段侵彻时,杆体头部形状又变为了蘑菇头形,可简化为半球形计算。忽略摩擦阻力,则后段单杆段的头形系数M和N分别为1和0.5。后段单杆段初始条件为l=65 mm,杆体速度v2为1 257.9 m/s,终止条件为侵彻速度降为零,结合式(19)~(21)以及侵彻深度变化式(10),可求得后段单杆段的侵彻深度x3为50 mm。
着靶速度1 310 m/s的前置组合杆体1垂直侵彻钢靶的总侵彻深度x即为三段侵彻深度之和,为82.9 mm。从数值模拟观察到前置组合杆体2、3的组杆段侵彻时杆体的头部形状分别如图 13~14所示。从图 13观察到前置组合杆体2的组杆段的头部形状为b=35D,D1=14D,代入式(31),求得N=0.31。从图 14观察到前置组合杆体3的组杆段的头部形状为b=23D,D1=12D,代入式(31),求得N=0.32。按照着靶速度1 310 m/s的前置组合杆体1的总侵彻深度的求解步骤,得到各阶段的速度变化和侵彻深度如表 4所示。计算得到所有试验工况总侵彻深度的理论计算值,并与表 3中试验值进行比较,如表 5所示。
表 4 侵彻过程中各阶段的速度变化和侵彻深度Table 4. Velocity variation and penetration depth in different stages of penetration process杆结构 开坑段 前置组杆段 单杆段 v0/(m·s-1) v1/(m·s-1) x1/mm v1/(m·s-1) v2/(m·s-1) x2/mm v2/(m·s-1) v3/(m·s-1) x3/mm 均质杆 1 356 1 342.0 11.0 1 342.0 0 71.2 前置组合杆体1 1 310 1 295.5 10.9 1 295.5 1 257.9 22.0 1 257.9 0 50.0 前置组合杆体2 1 320 1 305.7 10.9 1 305.7 1 251.3 29.8 1 251.3 0 46.1 前置组合杆体3 1 200 1 184.2 10.6 1 184.2 1 096.4 27.3 1 096.4 0 42.6 表 5 不同初速度下侵彻深度理论和试验对比Table 5. Comparison of penetration depth between theory and test at different initial velocities杆结构 v0/(m·s-1) 侵彻深度 ε/% 理论计算(x1+x2+x3)/mm 试验h/mm 均质杆 1 356 82.2 84 2.14 前置组合杆体1 1 310 82.9 83 0.12 前置组合杆体2 1 320 86.8 84 3.33 前置组合杆体3 1 200 80.5 78 3.21 从表 5中可以看出试验工况的理论计算值与试验值的误差均小于5%,这说明前置组合杆体垂直侵彻钢靶的计算模型的适用性,可用于前置组合杆体垂直侵彻钢靶的理论计算。从各个阶段的侵彻深度可以看出,开坑阶段,不同杆体结构侵彻深度基本相同。而在组杆侵彻段,能够明显体现出前置组合杆体优势,此阶段利用材料性能的不同,前置组合杆体形成结构自锐,降低了侵彻阻力,提高了其侵彻能力。
利用计算模型对图 6中直径为4 mm的这组数值模拟规律进行了对比分析,得到不同杆体结构下侵彻深度如表 6所示。从表 6中的数据对比可以看出,随着碳化钨小杆体长度的增长,理论计算的总侵彻深度的变化与数值模拟规律相同,可用数值模拟结合理论计算来为设计不同配置的更优化的前置组合杆体作依据。
表 6 不同杆结构侵彻深度数值模拟和理论对比Table 6. Comparison of penetration depth between simulation and theory with different rod structuresH1/mm 侵彻深度 ε/% 数值模拟h/mm 理论计算(x1+x2+x3)/mm 0 74.5 77.7 4.23 30 78.0 83.4 6.92 50 80.5 85.4 6.09 70 84.0 88.5 5.36 90 85.0 90.0 5.88 4. 结论
本文中开展了前置组合杆体侵彻钢靶的试验和数值模拟,通过比较相同工况的试验和数值模拟结果,验证了前置组合杆体侵彻性能优于相同外形结构的均质杆体,并通过观察侵彻过程,分析出前置组合杆体的组杆段在稳定侵彻阶段能形成更尖锐的头部形状,即通过不同性能材料组合达置组合杆体的侵彻深度与后者相近,这到了结构自锐效果,从而降低了所受的靶体阻力,提高了其侵彻能力。
基于数值模拟和试验结果,将前置组合杆体侵彻过程分为开坑段、组杆段、单杆段三个阶段,分别建立其侵彻模型,最后将之联立得到了计算前置组合杆体侵彻的简化模型。代入试验工况进行验证,理论模型计算值与试验值误差均小于5%,验证了该简化模型的适用性。此研究可为新型长杆体动能武器设计提供参考意义。
-
表 1 不同配置的前置组合杆体
Table 1. Different configurations of pre-composited rods
杆结构 小杆体直径d2/mm 小杆体长度H1/mm 均质杆 0 0 前置组合杆体1 1.5 25 前置组合杆体2 2.5 30 前置组合杆体3 5.5 30 表 2 不同配置的前置组合杆体
Table 2. Different configurations of pre-composited rods
材料 ρ/(g·cm-3) G/GPa σy/MPa γ 93钨 17.6 136 1 506 1.54 碳化钨 14.7 254 5 100 1.50 45钢 7.85 77 700 2.17 表 3 两组杆体头部形状图
Table 3. Nose shape of two rods
杆结构 v/(m·s-1) h/mm ε/% 试验 数值模拟 均质杆 1 356 84.0 81.5 2.98 前置组合杆体1 1 310 83.0 77.7 6.39 前置组合杆体2 1 320 84.0 80.9 3.70 前置组合杆体3 1 200 78.0 76.2 2.31 表 4 侵彻过程中各阶段的速度变化和侵彻深度
Table 4. Velocity variation and penetration depth in different stages of penetration process
杆结构 开坑段 前置组杆段 单杆段 v0/(m·s-1) v1/(m·s-1) x1/mm v1/(m·s-1) v2/(m·s-1) x2/mm v2/(m·s-1) v3/(m·s-1) x3/mm 均质杆 1 356 1 342.0 11.0 1 342.0 0 71.2 前置组合杆体1 1 310 1 295.5 10.9 1 295.5 1 257.9 22.0 1 257.9 0 50.0 前置组合杆体2 1 320 1 305.7 10.9 1 305.7 1 251.3 29.8 1 251.3 0 46.1 前置组合杆体3 1 200 1 184.2 10.6 1 184.2 1 096.4 27.3 1 096.4 0 42.6 表 5 不同初速度下侵彻深度理论和试验对比
Table 5. Comparison of penetration depth between theory and test at different initial velocities
杆结构 v0/(m·s-1) 侵彻深度 ε/% 理论计算(x1+x2+x3)/mm 试验h/mm 均质杆 1 356 82.2 84 2.14 前置组合杆体1 1 310 82.9 83 0.12 前置组合杆体2 1 320 86.8 84 3.33 前置组合杆体3 1 200 80.5 78 3.21 表 6 不同杆结构侵彻深度数值模拟和理论对比
Table 6. Comparison of penetration depth between simulation and theory with different rod structures
H1/mm 侵彻深度 ε/% 数值模拟h/mm 理论计算(x1+x2+x3)/mm 0 74.5 77.7 4.23 30 78.0 83.4 6.92 50 80.5 85.4 6.09 70 84.0 88.5 5.36 90 85.0 90.0 5.88 -
[1] FORRESTAL M J, LUK V K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid[J]. Journal of Applied Mechanics, 1988, 55(2):275-279. DOI: 10.1115/1.3173672. [2] ROSENBERG Z, DEKEL E. On the role of nose profile in long-rod penetration[J]. International Journal of Impact Engineering, 1999, 22(5):551-557. DOI: 10.1016/S0734-743X(98)00054-2. [3] JONES S E, RULE W K. On the optimal nose geometry for a rigid penetrator, including the effects of pressure-dependent friction[J]. International Journal of Impact Engineering, 2000, 24(4):403-415. DOI: 10.1016/S0734-743X(99)00157-8. [4] JONES S E, RULE W K, JEROME D M, et al. On the optimal nose geometry for a rigid penetrator[J]. Computational Mechanics, 1998, 22(5):413-417. DOI: 10.1007/s004660050373. [5] CHEN X W, LI Q M. Deep penetration of a non-deformable projectile with different geometrical characteristics[J]. International Journal of Impact Engineering, 2002, 27(6):619-637. DOI: 10.1016/S0734-743X(02)00005-2. [6] LI Q M, CHEN X W. Dimensionless formulae for penetration depth of concrete target impacted by a non-deformable projectile[J]. International Journal of Impact Engineering, 2003, 28(1):93-116.DOI: 10.1016/S0734-743X(02)00037-4. [7] CHIAN S C, TAN B C V, SARMA A. Projectile penetration into sand:Relative density of sand and projectile nose shape and mass[J]. International Journal of Impact Engineering, 2017, 103:29-37.DOI: 10.1016/j.ijimpeng.2017.01.002. [8] 程兴旺, 王富耻, 李树奎, 等.不同头部形状长杆弹侵彻过程的数值模拟[J].兵工学报, 2007, 28(8):930-933. DOI: 10.3321/j.issn:1000-1093.2007.08.007.CHENG Xingwang, WANG Fuchi, LI Shukui, et al. Numerical simulation on the penetrations of long-rod projectiles with different nose shapes[J]. Acta Armamentarii, 2007, 28(8):930-933. DOI: 10.3321/j.issn:1000-1093.2007.08.007. [9] 高光发, 李永池, 黄瑞源, 等.杆弹头部形状对侵彻行为的影响及其机制[J].弹箭与制导学报, 2012, 32(6):51-54. DOI: 10.3969/j.issn.1673-9728.2012.06.015.GAO Guangfa, LI Yongchi, HUANG Ruiyuan, et al. Effect of nose shape on penetration performance of long-rod penetrator and its mechanism[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(6):51-54. DOI: 10.3969/j.issn.1673-9728.2012.06.015. [10] 孙庚辰, 吴锦云, 赵国志, 等.长杆弹垂直侵彻半无限厚靶板的简化模型[J].兵工学报, 1981(4):1-8. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000005146030SUN Gengchen, WU Jinyun, ZHAO Guozhi, et al. A simplified model of the penetration of the long-rod penetrator against the plated with semi-infinite thickness at normal angle[J]. Acta Armamentarii, 1981(4):1-8. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK000005146030 [11] 吴群彪, 沈培辉, 刘荣忠, 等.长杆体稳定侵彻阶段头部形状的侵彻效率分析[J].兵器材料科学与工程, 2014, 37(3):80-83.DOI: 10.3969/j.issn.1004-244X.2014.03.023.WU Qunbiao, SHEN Peihui, LIU Rongzhong, et al. Long rod penetration efficiency analysis of nose shape at quasi-steady penetration stage[J]. Ordnance Material Science and Engineering, 2014, 37(3):80-83. DOI: 10.3969/j.issn.1004-244X.2014.03.023. 期刊类型引用(1)
1. 宋成俊,任建荣,李艳飞. 基于SPH法的不同材料弹芯侵彻半无限靶的数值模拟. 电子制作. 2020(12): 20-23 .  百度学术
百度学术其他类型引用(1)
-








 下载:
下载:













 下载:
下载:







 百度学术
百度学术