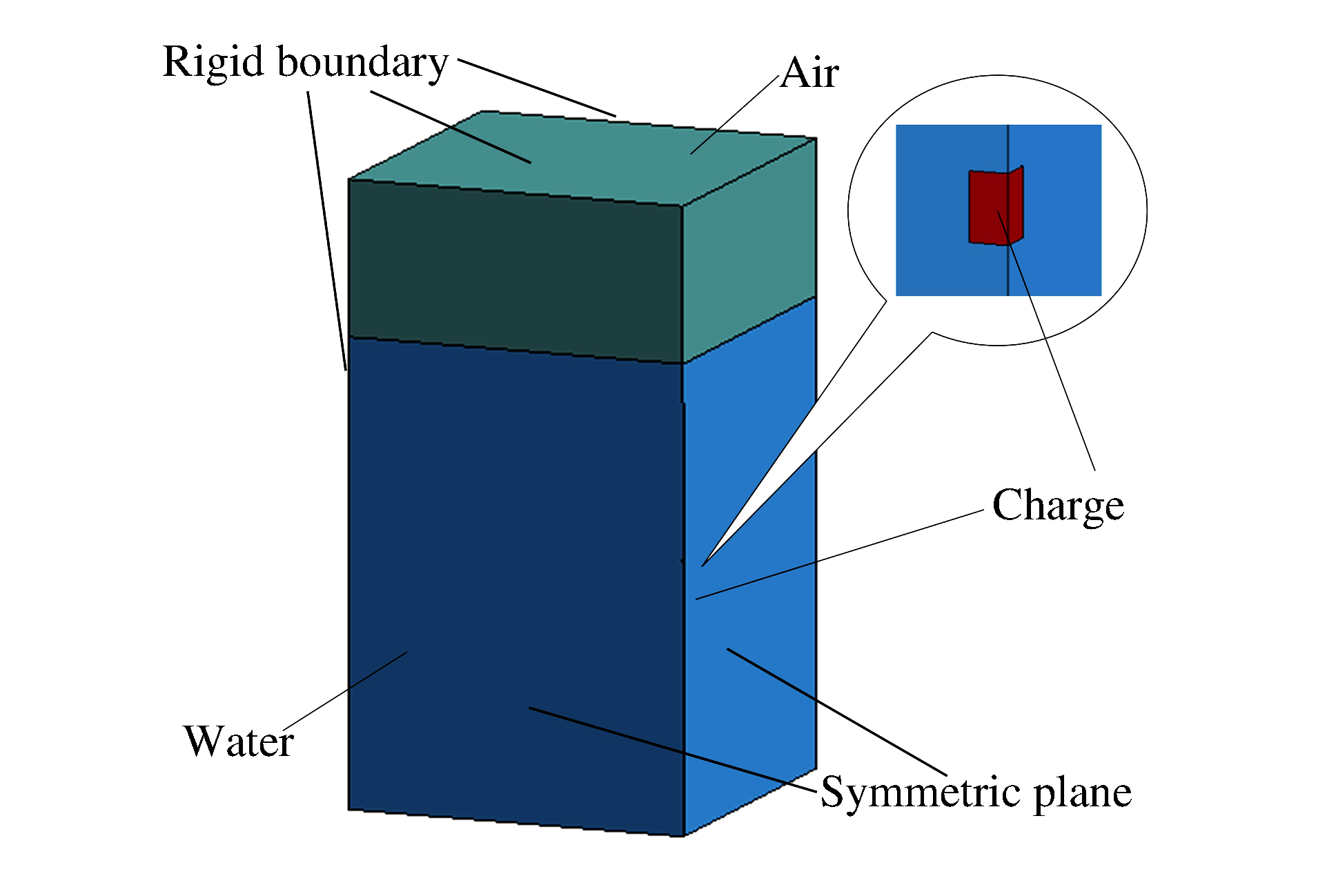
Similarity relations of underwater explosion in centrifuge and pressurizing vessels
-
摘要: 水下爆炸冲击波和气泡脉动的共同作用不能仅依据几何相似条件进行模型试验，相关的尺寸缩比模型试验可以借助密闭加压罐或离心机进行。通过量纲分析和π定理对模型试验的相似理论进行了推导，分别探讨了密闭加压容器和离心机中水下爆炸的相似关系及其适用范围，并对原型工况和尺寸缩比为1/20和1/30的模型工况基于LS-DYNA进行了数值模拟。结果表明：加压模型试验中水下爆炸冲击波、气泡脉动半径和周期可以满足相似关系，但是气泡迁移和射流不符合相似关系；离心模型试验中水下爆炸冲击波和气泡脉动基本完全相似。Abstract: The collective effect of underwater explosion shock wave and bubble pulsation does not meet the traditional geometric similarity relation, and the scaled model test must be carried out in a closed pressurized tank or centrifuge apparatus. Through the dimensional analysis and π theorem, the similarity theory of the model tests was deduced. The prototype condition and model conditions with the scaled ratio of 1/20 and 1/30 were simulated based on LS-DYNA, which shows the similarity relations and application scope of the pressurized model and centrifugal model. The shock wave, bubble radius and bubble period can meet the similarity relations but the bubble motion and jet can not meet the similarity relations in the pressurized model; and the shock wave and bubble pulsation almost meet the similarity relations in the centrifugal model.
-
Key words:
- underwater explosion /
- model test /
- centrifugal model /
- pressurized model /
- LS-DYNA
-
图 4 离心模型工况2和工况3的气泡半径数值结果
Figure 4. Numerical bubble radius histories under working conditions 2 and 3 of the centrifugal model
图 5 离心模型换算到原型的气泡半径数值结果
Figure 5. Numerical bubble radius histories for converting the centrifugal model into the prototype
图 6 离心模型工况2和工况3的冲击波数值结果
Figure 6. Numerical shock wave pressure-time curves under working conditions 2 and 3 of the centrifugal model
图 7 离心模型换算到原型的冲击波数值结果
Figure 7. Numerical shock wave pressure-time curves for converting the centrifugal model into the prototype
图 8 150 mg药量在0.170 8 MPa气压、37.5 cm水深下爆炸气泡脉动过程数值模拟结果(工况5)
Figure 8. The numerical simulated process of bubble pulsation of 150 mg charge in the water depth of 37.5 cm under the atmospheric pressure of 0.170 8 MPa (condition 5)
图 9 加压模型工况4和工况5的气泡半径数值结果
Figure 9. Numerical bubble radius histories under working conditions 4 and 5 of the pressurized model
图 10 加压模型换算到原型的气泡半径数值结果
Figure 10. Numerical bubble radius histories for converting the pressurized model into the prototype
图 11 加压模型工况4和工况5的冲击波数值结果
Figure 11. Numerical shock wave pressure-time curves under working conditions 4 and 5 of the pressurized model
图 12 加压模型换算到原型的冲击波数值结果
Figure 12. Numerical shock wave pressure-time curves for converting the pressurized model into the prototype
图 13 加压模型气泡垂直方向迁移运动的数值结果
Figure 13. Numerical vertical motion of the bubble for the pressurized model
图 14 加压模型换算到原型气泡垂直方向迁移运动的数值结果
Figure 14. Numerical vertical motion of the bubble for converting the pressurized model into the prototype
表 1 相似关系
Table 1. The similarity relations
参量分类 参数名称 原型参量 离心模型 加压模型 模型参量 参量缩比 模型参量 参量缩比 长度参数 装药半径 r λr λ λr λ 爆距 d λd λ λd λ 装药沉深 h λh λ λh λ 特征长度 l λl λ λl λ 速度参数 流速 v v 1 v 1 重力参数 加速度 ag ag/λ 1/λ ag 1 压力参数 大气压强 p0 p0 1 p0+ρ0agh(1-λ) 装药参数 装药质量 m λ3m λ3 λ3m λ3 冲击波参数 峰值压力 ps ps 1 ps 1 时间常数 τ λτ λ λτ λ 冲量 I λI λ λI λ 气泡参数 气泡半径 R λR λ λR λ 脉动周期 T λT λ λT λ 
下载: 导出CSV
表 2 工况设置
Table 2. The working conditions
模型 工况 m h/cm ag/g p0/MPa 长度缩比 mp/g hp/cm 原型 1 1 200 g 750.0 1 0.101 0 1 1 200 750.0 离心模型 2 50 mg 25.0 30 0.101 0 1/30 1 350 750.0 3 150 mg 37.5 20 0.101 0 1/20 1 200 750.0 加压模型 4 50 mg 25.0 1 0.172 1 1/30 1 350 750.0 5 150 mg 37.5 1 0.170 8 1/20 1 200 750.0
下载: 导出CSV
表 3 模型和原型数值计算结果对比
Table 3. Comparison of the numerical calculation results between the models and prototype
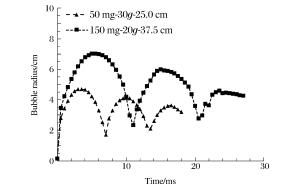
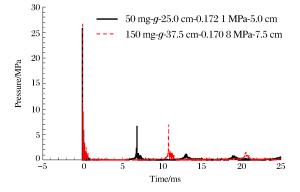
工况 工况参数 d/cm 模型 原型 m ag/g h/cm p/kPa ps/MPa Rmax/cm T/ms ps/MPa Rmax/cm T/ms 1 1 200 g 1 750.0 0.101 0 150.0 28.84 144.2 221.3 2 50 mg 30 25.0 0.101 0 5.0 25.80 4.95 6.82 25.80 148.5 204.6 3 150 mg 20 37.5 0.101 0 7.5 27.03 7.02 10.84 27.03 140.4 216.8 4 50 mg 1 25.0 0.172 1 5.0 25.80 4.69 6.85 25.80 140.7 205.5 5 150 mg 1 37.5 0.170 8 7.5 27.03 7.02 10.82 27.03 140.4 216.4
下载: 导出CSV
-
[1] COLE R H. Underwater explosion[M]. New Jersey:Princeton University Press, 1948. [2] MURPHY G. Similitude in engineering[M]. New York:Ronald Press Co., 1950. [3] GEL'FAND B E, TAKAYAMA K. Similarity criteria for underwater explosions[J]. Combustion, Explosion, and Shock Waves, 2004, 40(2):214-218. DOI: 10.1023/B:CESW.0000020144.55275.df. [4] 张效慈.水下爆炸试验相似准则[J].船舶力学, 2007, 11(1):108-118. DOI: 10.3969/j.issn.1007-7294.2007.01.014.ZHANG Xiaoci. Similarity criteria for experiment of underwater explosion[J]. Journal of Ship Mechanics, 2007, 11(1):108-118. DOI: 10.3969/j.issn.1007-7294.2007.01.014. [5] 张效慈.水下爆炸试验模型律的若干问题[J].船舶力学, 2009, 13(5):783-787. DOI: 10.3969/j.issn.1007-7294.2009.05.016.ZHANG Xiaoci. Some problems for model law of underwater explosion tests[J]. Journal of Ship Mechanics, 2009, 13(5):783-787. DOI: 10.3969/j.issn.1007-7294.2009.05.016. [6] 刘文韬, 姚熊亮, 李帅, 等.离心机水下爆炸缩比实验原理及数值研究[J].爆炸与冲击, 2016, 36(6):789-796. DOI: 10.11883/1001-1455(2016)06-0789-08.LIU Wentao, YAO Xiongliang, LI Shuai, et al. Experimental principle and numerical study of scaled-down underwater explosion model on a centrifuge apparatus[J]. Explosion and Shock Waves, 2016, 36(6):789-796. DOI: 10.11883/1001-1455(2016)06-0789-08. [7] SCHMIDT R M, HOUSEN K R. Some recent advances in the scaling of impact and explosion cratering[J]. International Journal of Impact Engineering, 1987, 5(1/4):543-560.DOI: 10.1016/0734-743X(87)90069-8. [8] HOUSEN K R, SCHMIDT R M, HOLSAPPLE K A. Crater eject a scaling laws:fundamental forms based upon dimensional analysis[J]. Journal of Geophysical Research, 1983, 88:2485-2499. DOI: 10.1029/JB088iB03p02485. [9] KUTTER B L, O'LEARY L M, THOMPSON P Y. Centrifugal modeling of the effect of blast loading on tunnels[C]//Addendum to Proceedings of the Second Symposium on the Interaction of Non-nuclear Munitions with Structures. Panama City Beach Florida, April 15-18, 1985. [10] 范一锴, 陈祖煜, 梁向前, 等.砂中爆炸成坑的离心模型试验分析方法比较[J].岩石力学与工程学报, 2011, 30:4123-4128. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201104561938FAN Yikai, CHEN Zuyu, LIANG Xiangqian, et al. Comparison of three methods for geotechnical centrifuge model tests of explosion cratering in sand[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30:4123-4128. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=QK201104561938 [11] 马立秋, 张建民, 胡耘, 等.地面爆炸条件下浅埋地下结构物响应的离心模型试验研究[J].岩石力学与工程学报, 2010, 29:3672-3678. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb2010z2032MA Liqiu, ZHANG Jianmin, HU Yun, et al. Centrifugal model tests for responses of shallow-buried underground structures under surface blasting[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29:3672-3678. http://d.old.wanfangdata.com.cn/Periodical/yslxygcxb2010z2032 [12] SONG Ge, CHEN Zuyu, LONG Yuan, et al. Experimental and numerical investigation of the centrifugal model for underwater explosion shock wave and bubble pulsation[J]. Ocean Engineering, 2017, 142:523-531.DOI: 10.1016/j.oceaneng.2017.04.035. [13] HU Jing, CHEN Zuyu, ZHANG Xuedong, et al. Underwater explosion in centrifuge:Part Ⅰ:validation and calibration of scaling laws[J]. Science China:Technological Sciences, 2017, 60(11):1638-1657. DOI: 10.1007/s11431-017-9083-0. [14] 马坤, 初哲, 王可慧, 等.小当量炸药深水爆炸气泡脉动模拟实验[J].爆炸与冲击, 2015, 35(3):320-325. DOI: 10.11883/1001-1455-(2015)03-0320-06.MA Kun, CHU Zhe, WANG Kehui, et al. Experimental research on bubble pulse of small scale charge exploded under simulated deep water[J]. Explosion and Shock Waves, 2015, 35(3):320-325. DOI: 10.11883/1001-1455-(2015)03-0320-06. [15] Livermore Software Technology Corporation. LS-DYNA[Z]. Livermore, CA, USA: Livermore Software Technology Corporation, 2012. [16] 李晓杰, 张程娇, 王小红, 等.水的状态方程对水下爆炸影响的研究[J].工程力学, 2014, 31(8):46-52. DOI: 10.6052/j.issn.1000-4750.2013.03.0180.LI Xiaojie, ZHANG Chengjiao, WANG Xiaohong, et al. Numerical study on the effect of equations of state of water on underwater explosions[J]. Engineering Mechanics, 2014, 31(8):46-52. DOI: 10.6052/j.issn.1000-4750.2013.03.0180. [17] LEE E, FINGER M, COLLINS W. JWL equation of state coefficients for high explosives: Rept-UCID-16189[R]. Lawrence Livermore National Laboratory, 1973. -
点击查看大图
计量
- 文章访问数: 6572
- HTML全文浏览量: 2004
- PDF下载量: 46
- 被引次数: 0