混凝土靶侵彻过程中空腔膨胀响应分区

牛振坤; 陈小伟; 邓勇军; 姚勇

doi:10.11883/bzycj-2017-0368

混凝土靶侵彻过程中空腔膨胀响应分区

doi: 10.11883/bzycj-2017-0368

牛振坤^1,,
陈小伟^{2, 3, ,},
邓勇军^{1, 2},
姚勇^{1, 2}

1.
西南科技大学土木工程与建筑学院, 四川绵阳 621010
2.
工程材料与结构冲击振动四川省重点实验室, 四川绵阳 621010
3.
北京理工大学前沿交叉科学研究院, 北京 100081

基金项目:

国家自然科学基金项目 11225213

国家自然科学基金项目 11390361

国家自然科学基金项目 11390362

西南科技大学研究生创新基金项目 16ycx089

详细信息

作者简介:
牛振坤(1991-), 男, 硕士研究生, 858767489@qq.com

通讯作者:
陈小伟(1967-), 男, 博士, 研究员, 博士生导师, chenxiaoweintu@bit.edu.cn

中图分类号: O347
计量
- 文章访问数: 5845
- HTML全文浏览量: 2456
- PDF下载量: 92
- 被引次数: 0
出版历程
- 收稿日期: 2017-10-14
- 修回日期: 2017-12-18
- 刊出日期: 2019-02-05

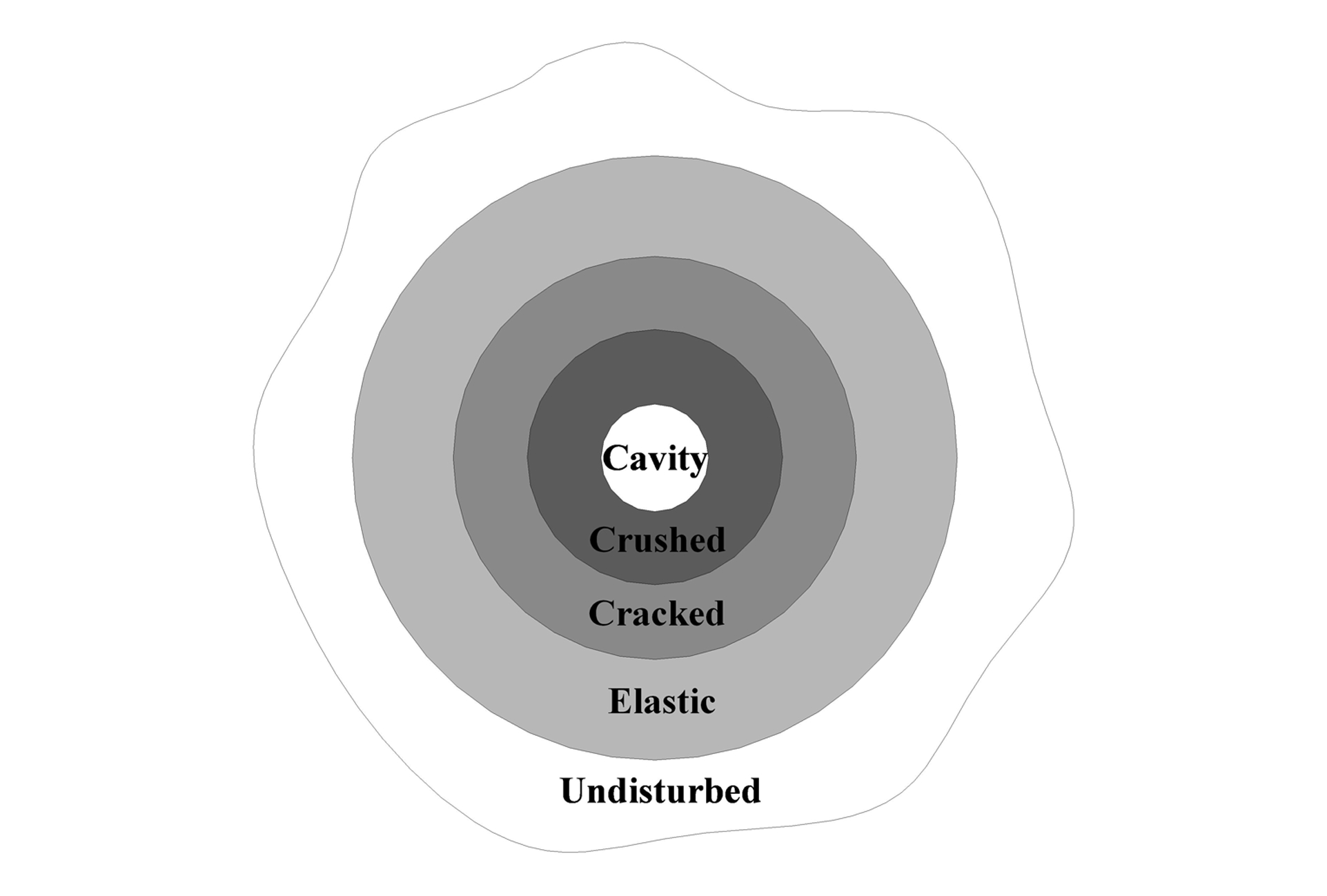
Cavity expansion response of concrete targets under penetration

NIU Zhenkun^1
,,
CHEN Xiaowei^{2, 3
, ,},
DENG Yongjun^{1, 2},
YAO Yong^{1, 2}

1.
School of Civil Engineering and Architecture, Southwest University of Science and Technology, Mianyang 621010, Sichuan, China
2.
Shock and Vibration of Engineering Materials and Structures Key Laboratory of Sichuan Province, Mianyang 621010, Sichuan, China
3.
Advanced Research Institute for Multidisciplinary Science, Beijing Institute of Technology, Beijing 100081, China

摘要

摘要: 利用LS-DYNA有限元软件对刚性弹正侵彻混凝土靶进行数值模拟，以混凝土极限压应变和极限拉应变两阈值为依据，对侵彻过程中混凝土靶空腔膨胀响应区域进行了识别划分，得到了侵彻过程中混凝土各响应区的区域大小。另外，还讨论了弹体侵彻速度对混凝土粉碎区和破裂区的影响，以及粉碎区和破裂区边界膨胀速度分别与侵彻速度的关系。计算结果表明，随着弹体侵彻速度的增大，混凝土粉碎区和破裂区界面速度都增大，粉碎区半径增大，而破裂区半径却减小；当侵彻速度达到某一特定值时，破裂区将会消失。
- 混凝土 /
- 侵彻 /
- 空腔 /
- 膨胀响应区 /
- 界面膨胀速度
Abstract: The LS-DYNA was used to simulate the process of a rigid projectile normally penetrating into a concrete target. Based on the two threshold values of ultimate compressive strain and ultimate tensile strain of the concrete, the cavity expansion response regions of the concrete target were identified and the size of each concrete response region in the penetration process was obtained. The effect of the penetration velocity on the crushed and cracked regions of the concrete was analyzed. The relationships between the boundary expansion velocity of the crushed/cracked regions and the penetration velocity were discussed. The results indicate that with increasing the initial impacting velocity, the interface velocities of the crushed/cracked regions and the radius of the crushed region increase, but the radius of the cracked region decreases. At last, the cracked region may disappear when the penetration velocity achieves a certain critical value.
- concrete /
- penetration /
- cavity /
- expansion response region /
- interface expansion velocity

HTML全文

图 1 混凝土动态球形空腔膨胀响应区域

Figure 1. Dynamic spherical cavity expansion response regions of concrete

下载: 全尺寸图片幻灯片

图 2 子弹和混凝土靶板的有限元模型

Figure 2. The finite element model for projectile and concrete target

下载: 全尺寸图片幻灯片

图 3 弹体以速度v₀=749 m/s正侵彻混凝土靶板的破坏状态

Figure 3. Damage of a concrete target penetrated by the projectlie the the initial velocity 749 m/s at different moments

下载: 全尺寸图片幻灯片

图 4 弹体侵彻混凝土靶板的数值模拟和实验^[11]结果

Figure 4. Numerical simulation and experimental^[11] results of a projectile penetration into a concrete target

下载: 全尺寸图片幻灯片

图 5 混凝土响应分区形成过程

Figure 5. Formation process of concrete target response regions

下载: 全尺寸图片幻灯片

图 6 弹尖运动到位置2时混凝土的应变云图

Figure 6. Strain diagram of the concrete when the projectile tip moves to position 2

下载: 全尺寸图片幻灯片

图 7 位置1、2和3处截面径向应变和环向应变随半径的变化曲线

Figure 7. Variation curves of radial strain and circumferential strain with radius at positions 1, 2 and 3

下载: 全尺寸图片幻灯片

图 8 各位置横剖切面计算结果以及分区大小

Figure 8. The results of each position cross section and the size of response regions

下载: 全尺寸图片幻灯片

图 9 混凝土靶纵剖切面图以及分区情况

Figure 9. Longitudinal section and response regions of concrete targets

下载: 全尺寸图片幻灯片

图 10 不同侵彻速度下的混凝土横剖切面位置1等效应变云图

Figure 10. The equivalent strain diagrams of concrete under different penetration velocities at position 1

下载: 全尺寸图片幻灯片

图 11 混凝土粉碎区和破裂区半径与侵彻速度的关系

Figure 11. Sizes of crushed /cracked regions varying with penetration velocity

下载: 全尺寸图片幻灯片

图 12 粉碎区和破裂区边界膨胀速度与侵彻速度的关系

Figure 12. Boundary expansion velocity of crushed/cracked regions varying with penetration velocity

下载: 全尺寸图片幻灯片

表 1 K&C模型中混凝土的材料参数

Table 1. Material parameters of concrete in the K&C model

密度/(kg·m^-3)	泊松比	σ_t/MPa	A₀/MPa	RSIZE	UCF
2 440	0.2	4	-48	3.94×10²	145

下载: 导出CSV

表 2 弹体的材料参数^[15]

Table 2. Material parameters of projectile^[15]

密度/(kg·m^-3)	弹性模量/GPa	泊松比	屈服强度/MPa	失效应变
7 910	210	0.3

下载: 导出CSV

表 3 弹体剩余速度

Table 3. Residual velocities of projectiles

初始速度/(m·s^-1)	剩余速度/(m·s^-1)
初始速度/(m·s^-1)	实验^[11]	模拟
301	0	0
381	136	157
434	214	234
606	449	454
749	615	616
1 058	947	936

下载: 导出CSV

参考文献(18)

[1]	FREW D J, FORRESTAL M J, CARGILE J D. The effect of concrete target diameter on projectile deceleration and penetration depth[J]. International Journal of Impact Engineering, 2006, 32(10):1584-1594. DOI: 10.1016/j.ijimpeng.2005.01.012.
[2]	武海军, 黄风雷, 金乾坤, 等.弹体贯穿钢筋混凝土数值模拟[J].爆炸与冲击, 2003, 23(6):545-550. doi: 10.3321/j.issn:1001-1455.2003.06.011 WU Haijun, HUANG Fenglei, JIN Qiankun, et al. Numerical simulation on perforation of reinforced concrete targets[J]. Explosion and Shock Waves, 2003, 23(6):545-550. doi: 10.3321/j.issn:1001-1455.2003.06.011
[3]	FORRESTAL M J, ALTMAN B S, CARGILE J D, et al. An empirical equation for penetration depth of ogive-nose projectiles into concrete targets[J]. International Journal of Impact Engineering, 1994, 15(4):395-405. DOI: 10.1016/0734-743X(94)80024-4.
[4]	CHEN Xiaowei, FAN S C, LI Qingmin. Oblique and normal perforation of concrete targets by a rigid projectile[J]. International Journal of Solids and Structures, 2004, 30(6):617-637. DOI: 10.1016/j.ijimpeng.2003.08.003.
[5]	FORRESTAL M J, LUK V K. Penetration into soil targets[J]. International Journal of Impact Engineering, 1992, 12(3):427-444. DOI: 10.1016/0734-743X(92)90167-R.
[6]	FORRESTAL M J, TZOU D Y. A spherical cavity-expansion penetration model for concrete targets[J]. International Journal of Solids and Structures, 1997, 34(31):4127-4146. DOI: 10.1016/S0020-7683(97)00017-6.
[7]	ROSENBERG Z, DEKEL E. A numerical study of the cavity expansion process and its application to long-rod penetration mechanics[J]. International Journal of Impact Engineering, 2008, 35(3):147-154. DOI: 10.1016/j.ijimpeng.2007.01.005.
[8]	ROSENBERG Z, DEKEL E. Analytical solution of the spherical cavity expansion process[J]. International Journal of Impact Engineering, 2009, 36(3):193-198. DOI: 10.1016/j.ijimpeng.2007.12.014.
[9]	王一楠, 黄风雷.混凝土材料动态球形空腔膨胀的数值模拟[J].北京理工大学学报, 2010, 30(1):5-9. DOI: 10.15918/j.tbit1001-0645.2010.01.010. WANG Yinan, HUANG Fenglei. Numerical simulation of dynamic spherical cavity expansion for concrete materials[J]. Transactions of Beijing Institute of Technology, 2010, 30(1):5-9. DOI: 10.15918/j.tbit1001-0645.2010.01.010.
[10]	李志康, 黄风雷.混凝土材料的动态空腔膨胀理论[J].爆炸与冲击, 2009, 29(01):95-101. DOI: 10.11883/1001-1455(2009)01-0095-06. LI Zhikang, HUANG Fenglei. A dynamic spherical cavity-expansion theory for concrete materials[J]. Explosion and Shock Waves, 2009, 29(1):95-101. DOI: 10.11883/1001-1455(2009)01-0095-06.
[11]	HANCHAK S J, FORRESTAL M J, YOUNG E R, et al. Perforation of concrete slabs with 48MPa (ksi) and 140MPa (20ksi) unconfined compressive strengths[J]. International Journal of Impact Engineering, 1992, 12(1):1-7. DOI: 10.1016/0734-743X(92)90282-X.
[12]	MALVAR L J, CRAWFORD J E, WESEVICH J W, et al. A plasticity concrete material model for DYNA3D[J]. International Journal of Impact Engineering, 1997, 19(9/10):847-873. DOI: 10.1016/S0734-743X(97)00023-7.
[13]	匡志平, 陈少群.混凝土K&C模型材料参数分析与模拟[J].力学季刊, 2015, 36(3):517-526. DOI: 10.15959/i.cnki.0254-0053.2015.03.019. KUANG Zhiping, CHEN Shaoqun. Analysis and simulation for the material parameters of K&C concrete model[J]. Chinese Quarterly of Mechanics, 2015, 36(3):517-526. DOI: 10.15959/i.cnki.0254-0053.2015.03.019.
[14]	Livermore Software Technology Corporation. LS-DYNA keyword user's manual(971)[M]. Livermore:Livermore Software Technology Corporation, 2007.
[15]	邓勇军, 陈小伟, 姚勇, 等.基于细观混凝土模型的刚性弹体正侵彻弹道偏转分析[J].爆炸与冲击, 2017, 37(3):377-386. DOI: 10.11883/1001-1455(2017)03-0377-10. DENG Yongjun, CHEN Xiaowei, YAO Yong, et al. On ballistic trajectory of rigid projectile normal penetration based on a meso-scopic concrete model[J]. Explosion and Shock Waves, 2017, 37(3):377-386. DOI:10.11883/1001- 1455(2017)03-0377-10.
[16]	朱伯龙, 董振祥.钢筋混凝土非线性分析[M].上海:同济大学出版社, 1985:1-26.
[17]	吕西林, 金国方, 吴晓涵.钢筋混凝土非线性有限元理论与应用[M].上海:同济大学出版社, 1997:7-34.
[18]	何丽灵, 陈小伟, 徐伟芳, 等.加速度计预埋法测量弹体侵深的机理分析[J].防护工程, 2014, 36(2):21-25. HE Liling, CHEN Xiaowei, XU Weifang, et al. Analysis on mechanism of pre-buried accelerometer method for DOP measurement[J]. Protective Engineering, 2014, 36(2):21-25.