Explosion overpressure of hydrogen cloud in catalytic reforming process
-
摘要: 基于计算流体力学分析软件（FLACS），以催化重整反应单元为例建立事故模型，研究不同形状障碍物、泄漏位置，对不同泄漏时间和泄漏监测点的氢气爆炸超压的影响情况。通过研究，建立了与气体燃烧热与爆炸监测点距气团中心距离相关的最大爆炸超压模型。研究结果表明，在研究设计的遮挡物条件下，气体爆炸最大超压与折合距离在对数坐标系中均呈近似线性关系；对于不同的遮挡物，爆炸超压模型需进行修正；在反应器中部发生的事故场景，泄漏5 min后最大爆炸超压明显增大。Abstract: Because the structure and shape of processing equipment in petrochemical industry are complex normally, the explosion overpressure of gas is hard to be predicted by traditional explosion overpressure models. Base on the computational fluid dynamics software (FLACS) and the accident model of the catalytic reforming process, the effects of different factors (obstacle shape, leakage position) on the explosion overpressure of hydrogen at different times and different monitoring points were investigated. The explosion overpressure models for overpressure, combustion heat of hydrogen and distance from the center of gas cloud were established. The results show that, the overpressure approximately follows a linear relationship with scaled distance in a logarithmic coordinate system; the explosion overpressure model should be modified for different kinds of obstacles; when the leakage time achieves 5 minutes, the accident occurring in the middle of the reactor shows increasing overpressure obviously.
-
Key words:
- catalytic reforming process /
- hydrogen /
- explosion /
- overpressure
-
图 1 几何模型及点火位置、监测点示意图
Figure 1. Schematic diagrams for the geometric model, ignition positions and some overpressure monitors
图 2 引火点1气体爆炸最大超压与折合距离的关系
Figure 2. Relationship between maximum overpressure and scaled distance from explosion source centre for ignition position 1
图 3 引火点2气体爆炸最大超压与折合距离的关系
Figure 3. Relationship between maximum overpressure and scaled distance from explosion source centre for ignition position 2
图 4 对数坐标系下引火点2气体爆炸最大超压与折合距离的关系
Figure 4. Relationship between maximum overpressure and scaled distance from explosion source centre in a bilogarithmic coordinates systemfor ignition position 2
表 1 典型催化重整工艺火灾/爆炸事故
Table 1. Fire/explosion accidents in catalytic reforming process
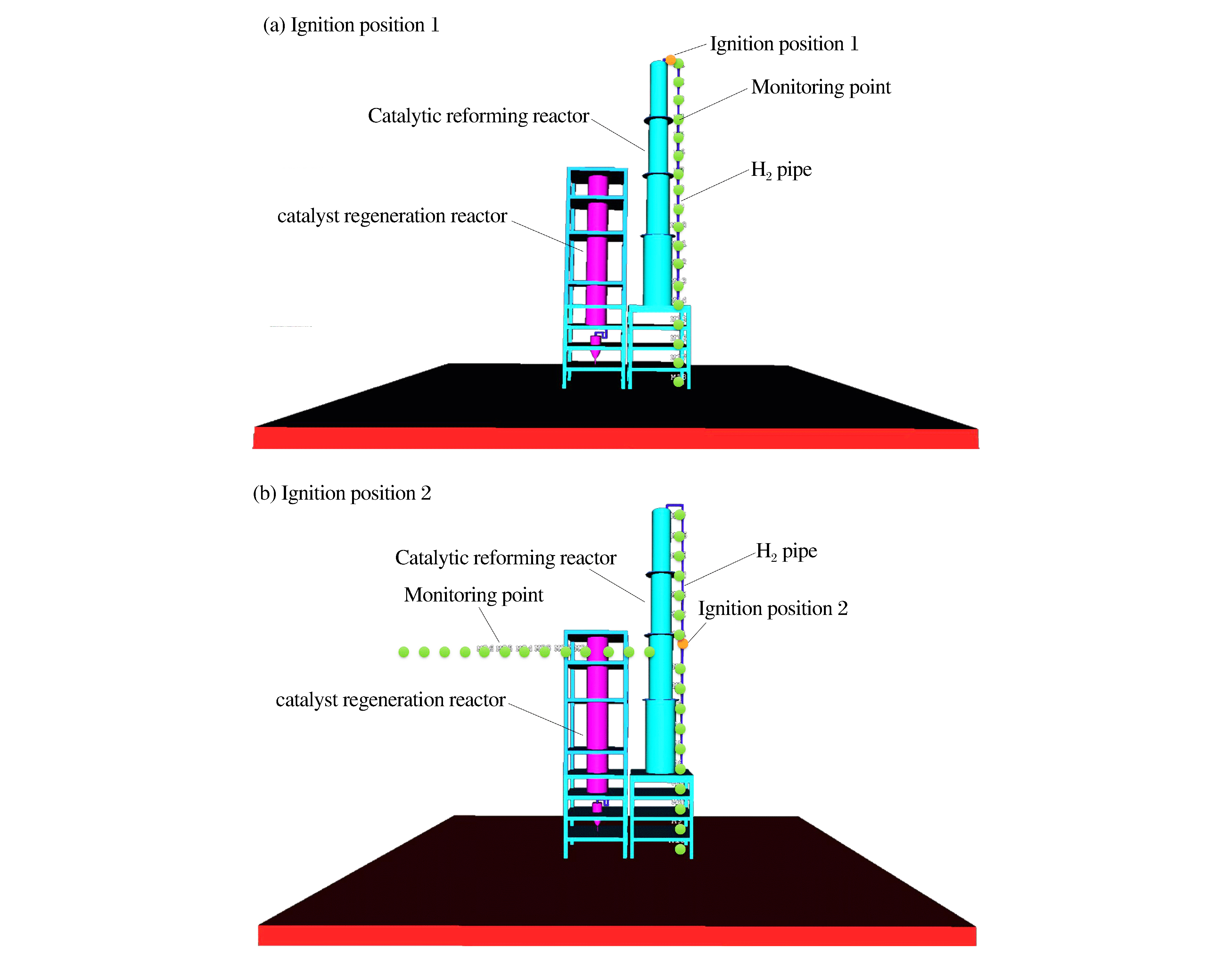
时间 设备 类型 物料 原因 2008年9月12日 PSA单元 爆炸 氢气 管线弯头破裂，导致氢气泄漏 2015年4月6日 吸附分离单元 爆炸/燃烧 混合芳烃 管道焊口断裂，混合芳烃泄漏 
下载: 导出CSV
表 2 引火点1不同泄漏时间氢气-空气气团爆炸最大超压
Table 2. Maximum overpressure of H2-air cloud explosion in ignition position 1
距离/m pmax/Pa 1 min 3 min 5 min 7 min 1 4.97×103 4.40×103 3.99×103 3.73×103 4 5.67×103 4.39×103 4.01×103 3.73×103 7 6.09×103 5.47×103 4.49×103 3.86×103 10 3.77×103 4.57×103 4.75×103 5.51×103 13 2.88×103 3.25×103 3.10×103 3.72×103 16 2.35×103 2.63×103 2.51×103 2.66×103 19 1.97×103 2.18×103 2.06×103 2.19×103 22 1.66×103 1.81×103 1.68×103 1.83×103 25 1.44×103 1.53×103 1.42×103 1.59×103 28 1.26×103 1.30×103 1.24×103 1.40×103 31 1.10×103 1.10×103 1.08×103 1.19×103 34 9.78×102 9.72×102 9.62×102 1.03×103 37 8.92×102 8.92×102 8.60×102 8.82×102 40 8.47×102 8.51×102 7.93×102 7.98×102 43 7.88×102 7.38×102 5.81×102 6.14×102 46 8.29×102 7.20×102 5.70×102 6.27×102 49 8.84×102 6.93×102 5.49×102 6.29×102 52 9.27×102 6.88×102 5.55×102 6.43×102
下载: 导出CSV
表 3 引火点1上方不同氢气泄漏时间模拟公式a、b系数及决定系数r2
Table 3. Values of a, b and r2 in each formula of H2 in ignition position 1 for different leakage times
泄漏时间/min a b r2 1 -0.97 -1.86 0.955 9 3 -1.211 -2.05 0.994 1 5 -1.341 -2.20 0.991 7 7 -1.361 -2.23 0.989 6
下载: 导出CSV
表 4 引火点2不同泄漏时间氢气-空气气团爆炸最大超压
Table 4. Maximum overpressure of H2-air cloud explosion in ignition position 2
相对方位 距离/m pmax/Pa 1 min 3 min 5 min 7 min 气团中心下方 2.5 5.09×103 6.20×103 1.73×104 1.82×104 5.5 7.13×103 6.38×103 1.53×104 1.59×104 8.5 3.67×103 6.99×103 1.29×104 1.32×104 11.5 3.16×103 6.56×103 1.27×104 1.10×104 14.5 2.69×103 5.46×103 1.15×104 1.07×104 17.5 2.52×103 5.42×103 1.56×104 1.33×104 20.5 1.95×103 3.54×103 5.97×103 5.67×103 23.5 2.02×103 3.59×103 6.62×103 5.99×103 26.5 2.14×103 3.66×103 6.02×103 5.81×103 29.5 2.27×103 3.84×103 6.84×103 6.87×103 气团中心上方 2.5 5.03×103 6.10×103 1.74×104 1.85×104 5.5 6.87×103 6.26×103 1.48×104 1.54×104 8.5 4.30×103 7.50×103 1.36×104 1.23×104 11.5 3.32×103 5.94×103 1.21×104 9.15×103 14.5 2.60×103 4.67×103 1.17×104 1.00×104 17.5 2.14×103 3.79×103 1.00×104 8.23×103 20.5 1.79×103 3.09×103 8.27×103 6.50×103 气团中心平行位置 4.5 6.20×103 6.66×103 1.48×104 1.58×104 7.5 5.40×103 7.07×103 1.31×104 1.26×104 10.5 5.09×103 7.69×103 1.72×104 1.40×104 13.5 2.85×103 5.05×103 1.41×104 1.30×104 16.5 2.22×103 4.38×103 1.30×104 1.26×104 19.5 1.81×103 3.72×103 1.08×104 1.04×104 22.5 1.53×103 3.11×103 8.99×103 8.08×103 25.5 1.32×103 2.57×103 7.27×103 6.32×103 28.5 1.14×103 2.10×103 5.95×103 4.97×103 31.5 9.52×102 1.65×103 4.78×103 3.96×103 34.5 7.37×102 1.24×103 3.76×103 3.23×103 37.5 4.78×102 8.08×102 2.71×103 2.49×103 40.5 1.69×102 3.00×102 1.15×103 1.06×103
下载: 导出CSV
表 5 引火点2上方不同氢气泄漏时间模拟公式a、b系数及决定系数r2
Table 5. Values of a, b and r2 in each formula of H2above ignition position 2 for different leakage times
泄漏时间/min a b r2 1 -1.00 -1.85 0.996 2 3 -1.01 -1.77 0.987 8
下载: 导出CSV
-
[1] 孙贤胜, 钱兴坤, 姜学峰.2015年国内外油气行业发展报告[M].北京:石油工业出版社, 2016:1-30. [2] 张秀华, 段忠东, 李玉顺.燃气爆炸冲击加载试验研究与数值模拟[J].振动与冲击, 2015, 34(10):142-146. DOI: 10.13465/j.cnki.jvs.2015.10.024.ZHANG Xiuhua, DUAN Zhongdong, LI Yushun. Tests and numerical simulation for gas blast shock loading[J]. Journal of Vibration and Shock, 2015, 34(10):142-146. DOI: 10.13465/j.cnki.jvs.2015.10.024. [3] MERCX W P M, BERG A C Van Den, HAYHURS C J, et al. Developments in vapour cloud explosion blast modeling[J]. Journal of Hazardous Materials, 2000, 71(1):301-319. DOI: 10.1016/S0304-3894(99)00085-0. [4] LOBATO J, CAIZARES P, RODRIGO M A, et al. A comparison of hydrogen cloud explosion models and the study of the vulnerability of the damage caused by an explosion of H2[J]. International Journal of Hydrogen Energy, 2006, 31(12):1780-1790. DOI: 10.1016/j.ijhydene.2006.01.006. [5] 宋元宁, 于立友, 李彩霞.TNT当量法预测某石化设备爆炸后果评价[J].中国安全生产科学技术, 2005, 1(3):66-68. DOI: 10.3969/j.issn.1673-193X.2005.03.017.SONG Yuanning, YU Liyou, LI Caixia. TNT equivalent method predicts the consequence that some petrochemical industry equipment explodes[J]. Journal of Safety Science and Technology, 2005, 1(3):66-68. DOI: 10.3969/j.issn.1673-193X.2005.03.017. [6] VAN DEN BERG A C. The multi-energy method:a framework for vapour cloud explosion blast prediction[J]. Journal of Hazardous Materials, 1985, 12(1):1-10. DOI: 10.1016/0304-3894(85)80022-4. [7] 曹勇, 郭进, 胡坤伦, 等.点火位置对氢气-空气预混气体泄爆过程的影响[J].爆炸与冲击, 2016, 36(6):847-852. DOI: 10.11883/1001-1455(2016)06-0847-06.CAO Yong, GUO Jin, HU Kunlun, et al. Effect of ignition locations on vented explosion of premixed hydrogen-air mixtures[J]. Explosion and Shock Waves, 2016, 36(6):847-852. DOI: 10.11883/1001-1455(2016)06-0847-06. [8] 程关兵, 李俊仙, 李书明, 等.氢气/丙烷/空气预混气体爆轰性能的实验研究[J].爆炸与冲击, 2015, 35(2):249-254. DOI: 10.11883/1001-1455(2015)02-0249-06.CHENG Guanbing, LI Junxian, LI Shuming, et al. An experimental study on detonation characteristics of binary fuels hydrogen/propane-air mixtures[J]. Explosion and Shock Waves, 2015, 35(2):249-254. DOI: 10.11883/1001-1455(2015)02-0249-06. [9] 杜扬, 李国庆, 王世茂, 等.障碍物数量对油气泄压爆炸特性的影响[J].化工学报, 2017, 68(7):2946-2955. DOI: 10.11949/j.issn.0438-1157.20161612.DU Yang, LI Guoqing, WANG Shimao, et al. Effects of obstacle number on the characteristics of vented gasoline-air mixture explosions[J]. Journal of Chemical Industry and Engineering (China), 2017, 68(7):2946-2955. DOI: 10.11949/j.issn.0438-1157.20161612. [10] NA'INNA A M, PHYLAKTOU H N, ANDREWS G E. The acceleration of flames in tube explosions with two obstacles as a function of the obstacle separation distance[J]. Journal of Loss Prevention in the Process Industries, 2013, 26(6):1597-1603. DOI: 10.1016/j.jlp.2013.08.003. [11] 余明高, 袁晨樵, 郑凯.管道内障碍物对加氢甲烷爆炸特性的影响[J].化工学报, 2016, 67(12):5311-5319. DOI: 10.11949/j.issn.0438-1157.20160645.YU Minggao, YUAN Chenqiao, ZHENG Kai. Effects of hydrogen addition on explosion characteristics of gas under condition of obstacles[J]. Journal of Chemical Industry and Engineering (China), 2016, 67(12):5311-5319. DOI: 10.11949/j.issn.0438-1157.20160645. [12] LI Dong, ZHANG Qi, MA Qiuju, et al. Influence of built-in obstacles on unconfined vapor cloud explosion[J]. Journal of Loss Prevention in the Process Industries, 2016, 43:449-456. DOI: 10.1016/j.jlp.2016.07.007. [13] NA'INNA A M, SOMUANO G B, PHYLAKTOU H N, et al. Flame acceleration in tube explosions with up to three flat-bar obstacles with variable obstacle separation distance[J]. Journal of Loss Prevention in the Process Industries 2015, 38:119-124. DOI: 10.1016/j.jlp.2015.08.009. [14] 徐承恩.催化重整工艺与工程[M].北京:中国石化出版社, 2014:1-17. [15] 赵劲松.化工过程安全[M].北京:化学工业出版社, 2015:103-106. [16] 史文虎.氢气燃烧与爆炸原因浅析[J].华北电力技术, 1991(7):54-60. DOI: 10.16308/j.cnki.issn1003-9171.1991.07.010.SHI Wenhu. Simple analysis of the reasons of hydrogen combustion and explosion[J]. North China Electric Power, 1991(7):54-60. DOI: 10.16308/j.cnki.issn1003-9171.1991.07.010. [17] 郭丹彤, 吕淑然, 杨凯.障碍物布置对气体爆炸压力场的影响效果研究[J].中国安全生产科学技术, 2015, 11(9):88-93. DOI: 10.11731/j.issn.1673-193x.2015.09.014.GUO Dantong, LÜ Shuran, YANG Kai. Research on impact effect of obstacle arrangement to pressure field of gas explosion[J]. Journal of Safety Science and Technology, 2015, 11(9):88-93. DOI: 10.11731/j.issn.1673-193x.2015.09.014. -
计量
- 文章访问数: 8315
- HTML全文浏览量: 2164
- PDF下载量: 43
- 被引次数: 0