D型战斗部破片飞散性及威力场快速计算

李翔宇; 李振铎; 梁民族

doi:10.11883/bzycj-2017-0420

D型战斗部破片飞散性及威力场快速计算

doi: 10.11883/bzycj-2017-0420

国防科技大学文理学院，湖南长沙 410073

基金项目: 国家自然科学基金（11202237）

详细信息

作者简介:
李翔宇（1980－），男，博士，副教授，xiangyulee@nudt.edu.cn

中图分类号: O385;TJ413
计量
- 文章访问数: 5561
- HTML全文浏览量: 2114
- PDF下载量: 80
- 被引次数: 14
出版历程
- 收稿日期: 2017-11-17
- 修回日期: 2018-07-01
- 网络出版日期: 2019-03-25
- 刊出日期: 2019-04-01

Dispersion properties and rapid calculation of fragment force field of D-shaped fragmentation warhead

College of Liberal Art and Science, National University of Defense Technology, Changsha 410073, Hunan, China

摘要

摘要: 破片威力场的快速计算是实现战斗部对目标快速评估的关键之一，本文中分别对型面宽度为 90°、120° 和 150° 三种 D 型战斗部的破片飞散规律进行实验和数值模拟研究，考察型面宽度和起爆模式对破片威力场的影响规律。结果表明：三种结构中包含 90% 破片的方位角分别为 21.16°、23.88° 和 30.08°；偏心线起爆和双端面偏心起爆，在 20° 方位角内破片总能量分别是周向均匀战斗部中心起爆能量的 3.4 倍和 3.3 倍；基于三种典型型面的破片威力场公式，通过构建二次插值函数获得其他型面战斗部的破片分布，为D型战斗部破片威力场的快速计算提供了一种有效方法。
- D型战斗部 /
- 破片飞散 /
- 起爆模式 /
- 快速计算
Abstract: Rapid calculation of the fragment force field is a key technique for quick damage assessment of warhead to target. In this work we carried out experiment and simulation on the dispersion patterns of three D-shaped warheads with the angle 90°, 120° and 150° and investigated the influences of the shape’s width and detonation mode on the distribution of the fragment force field. The results showed that 90% of the fragments in the three structures had azimuths of 21.16°, 23.88° and 30.08°, respectively; the eccentric line detonation and the two ends’ eccentric detonations were found to be better detonation modes, and the total energy of the fragments in 20° azimuth was respectively 3.4 and 3.3 times higher than the energy of the conventional fragmentation warhead. Based on the rapid calculation formulas of the fragment field of three typical shapes, we proposed that the force field of differently shaped warheads were obtained by constructing the quadratic interpolation function, providing an effective method for rapidly analyzing the distribution of the fragment field in the D-shaped warhead.
- D-shaped warhead /
- fragment dispersion /
- detonation mode /
- rapid calculation

HTML全文

定向战斗部^[1-3]一般通过特殊的结构设计和起爆控制，在破片飞散之前运用一些机构适时调整破片攻击方向，使破片在一定范围内相对集中，提高战斗部对目标的毁伤效率。目前研究较多的定向战斗部包括偏心起爆^[4-5]、可变形、动能杆、破片芯和可控旋转战斗部等，其中可变形战斗部具有良好的军事应用前景。可变形战斗部是在主装药起爆前通过起爆目标方向的辅助装药使壳体变形，从原来的对称结构变成非对称的D型结构，将战斗部的环向破片更多地集中在目标方向，提高目标方向的破片密度，实现对目标的高效毁伤。因此，D型结构是可变形战斗部弹体变形型面的重要参考，研究D型战斗部的破片飞散特性对于可变形战斗部设计具有重要的指导意义。龚柏林等^[6]、王马法等^[7-8]、李振铎等^[9]采用实验和数值模拟方法初步研究了D型结构的破片飞散特性，获得了D型结构破片能量分布特性规律。

目前，国内外多家单位采用射击线^[10-12]方法建立了典型目标的毁伤评估模型及程序。采用射击线描述破片飞散区参数的方法主要有两种，一是利用经验公式进行估算，二是利用有限元软件对破片飞散区的形成过程进行数值模拟。对于传统周向均匀战斗部，经验公式能够很好地估算各种装填结构下的破片飞散分布。然而对于D型定向战斗部，能够合理描述破片飞散分布的经验公式较少。因此，本文中分别对型面宽度为90°、120° 和150° 三种D型战斗部的破片飞散规律进行实验和数值模拟研究，考察型面宽度和起爆模式对破片威力场的影响规律，拟合出快速计算D型结构破片威力场的计算公式。

1. 实　验

1.1 实验装置及弹靶布置

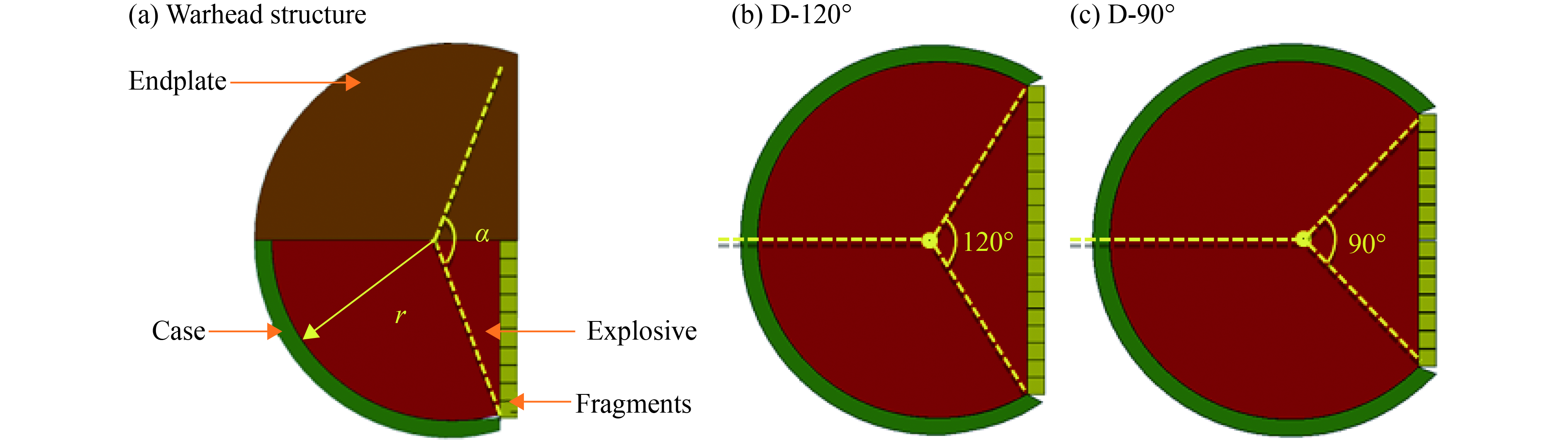
图1(a)为D型战斗部实验装置示意图，包括壳体、装药和端盖。壳体包括形成自然破片的圆弧段和形成预制破片的直线段，壳体厚度0.48 cm、高度8 cm、内径10 cm，材料为45钢；直线段壳体采用横向和纵向刻槽控制破片形状，刻槽深度为0.38 cm，相邻刻槽间距为0.48 cm；圆弧段对应的半径为r，直线段两端与圆心夹角定义为方位角α，直线段中间对应方位角为0°，图1(b)和(c)圆心角分别为120° 和90°，记为D-120° 和D-90°；直线段和圆弧段壳体边界采用焊接连接。端盖为厚度1.0 cm的LY12硬铝，用螺钉与壳体铆接。装药形状与壳体一致，外径10 cm、高度8 cm，材料为TNT。

图 1 D型战斗部结构示意图

Figure 1. Illustration of D-shaped warheads

下载: 全尺寸图片幻灯片

弹靶相对位置布置如图2所示，其中弹靶间距为350 cm，直线段正方向布置3块宽100 cm、高250 cm靶板，用网格线将靶板分成多个边长25 cm的正方形，每块靶板对应方位角为8.18°。靶板从左向右依次编号为1#、2#、3#，通过靶板记录破片的空间分布。靶板上布置测速靶网，采用通断靶网和高速摄影记录破片着靶信号，进而获得破片的空间分布和速度分布。

图 2 弹靶布置图

Figure 2. Layout of warhead and target

下载: 全尺寸图片幻灯片

1.2 实验结果及分析

通过靶板上破片着靶位置及数量统计，得到破片密度分布和破片数占比随方位角变化结果，如图3所示。可以看出，三种结构在8.18°方位角范围内的破片密度基本持平，而后破片密度随方位角迅速下降。统计表明，D-90°、D-120°、D-150° 三种结构在24.54° 方位角内破片数分别为破片总数的95.89%、91.92%、83.23%。利用Boltzmann分布对破片比例随方位角变化曲线进行拟合，得到D-90°、D-120° 和D-150°结构中包含90%破片的方位角范围分别为21.16°、23.88° 和30.08°。

图 3 破片密度分布和破片数比例随方位角变化图

Figure 3. Variation of fragment density distribution and fragment ratio with azimuthal angle

下载: 全尺寸图片幻灯片

图4(a)给出了每块靶板上首次着靶时刻的高速摄影照片，图4(b)给出了基于高速摄影和靶网得到的破片速度。对比发现，D-90° 结构在0° 方位角处的破片速度最大，D-150° 结构的破片速度最小，且破片速度近似呈高斯正态分布。主要原因是型面宽度较小的结构，爆轰波驱动破片的有效装药多，因而破片获得较高速度；随着方位角的增加，爆轰波从垂直入射逐渐变成斜入射甚至发生马赫反射，致使爆轰波对破片驱动加速能力降低，造成不同型面宽度下相同方位角处破片速度的差距逐步缩小。

图 4 破片着靶高速摄影照片及破片速度结果

Figure 4. High-speed photography of the target and the experimental results of fragment velocity

下载: 全尺寸图片幻灯片

2. 数值模拟

2.1 计算模型及材料参数

针对实验装置建立相同结构的有限元模型，如图5(a)所示。采用LS-DYNA软件中流固耦合算法计算炸药爆轰驱动破片飞散过程，空气和炸药为Euler网格，端盖、壳体和破片为Lagrange网格。采用高能炸药材料和JWL状态方程描述炸药爆轰过程。采用线性多项式状态方程来描述空气介质特性，并施加压力外流边界条件。采用Grüneisen状态方程和流体弹塑性材料模型描述壳体和端盖的动态响应行为。采用随动硬化材料模型描述破片动态响应。图5(b)为直线段预制破片在某个时刻的空间分布图，可以看出破片变形很小，基本保持形状。

图 5 D型战斗部有限元模型

Figure 5. Finite element model of D-shaped warhead

下载: 全尺寸图片幻灯片

2.2 与实验结果对比

图6(a)给出了D-90° 模型在350 cm处靶板上的破片分布的数值模拟结果，图中每一点代表一枚破片，纵坐标为破片高度位置，横坐标为破片位置对应的方位角，破片着靶速度在图上以不同颜色区分。可以看出，方位角0° 位置处的破片比较集中，速度最大；上下和左右边缘处的破片密度和速度都较小。图6(b)～(d) 分别给出了三种D型战斗部破片飞散的实验与数值模拟结果，结果表明D-90°、D-120° 和D-150° 三种结构中包含90%破片的方位角分别为18.4°、25.2° 和30°，与实验结果吻合较好。

图 6 三种D型战斗部破片分布结果

Figure 6. Fragment distributions of three D-shaped warheads

下载: 全尺寸图片幻灯片

图7给出了D-90°、D-120°和D-150°三种D型战斗部破片速度的实验和数值模拟结果，破片速度呈现中间高、两侧低的趋势，破片速度分布规律基本一致，近似符合高斯正态分布。

图 7 三种D型战斗部破片速度的实验和数值模拟结果

Figure 7. Fragment velocities of two D-shaped warheads

下载: 全尺寸图片幻灯片

2.3 破片飞散规律及分析

为了考察起爆方式对破片分布的影响，对D-120° 结构在几何中心起爆1、上端面中心起爆2、双端面中心起爆3、中心线起爆4、偏心点起爆5、上端面偏心起爆6、双端面偏心起爆7和偏心线起爆8等8种起爆方式下破片飞散特性进行分析，八种起爆模式如图8(a)所示。以周向均匀战斗部中心起爆的能量分布为参考基准，得到破片能量密度随方位角变化的曲线，如图8(b)所示。可以看出，D型战斗部破片在目标方向上能量聚焦明显，通过选择合理的起爆模式能够使杀伤能量在目标方向上相对集中。偏心起爆下目标方向上的破片至起爆点的距离大，对应有效装药量多，作用在破片上的抛射能量相对较大，所以偏心起爆下能量聚焦效果更佳。偏心起爆的四种模式中，偏心线起爆和双端面偏心起爆在目标方向上的能量聚焦能力强且总能量输出较高，20° 方位角内破片总能量分别是圆柱形中心起爆能量的3.4倍和3.3倍。

图 8 不同起爆方式下破片能量分布

Figure 8. Fragment energy distribution in different denotation modes

下载: 全尺寸图片幻灯片

为了考察型面宽度对破片飞散区域的影响，对60°、90°、120° 和150° 的四种型面宽度的战斗部在端面偏心起爆下破片飞散过程进行研究，得到破片能量密度和破片总能量随方位角变化结果，如图9所示。结果表明，D-60° 结构由于接近于圆柱形，其破片密度变化相对不明显，能量分布规律趋向于周向均匀战斗部。型面宽度在90°～120° 之间时目标方向能量增益较为明显，在0° 方位角附近型面宽度越小破片能量密度越大，在12° 方位角附近破片能量密度基本持平并开始以较快的速度衰减，40°～60° 方位角范围内破片的能量密度存在一个平台段。D-150° 型面宽度较大，但在350 cm的弹靶距离下破片总能量和能量聚焦能力并不能达到最佳；D-90° 和D-120° 两种结构在42° 方位角内的破片总能量与能量聚焦能力接近且为几种结构中最高。相对于周向均匀战斗部，D-90° 战斗部在43.2° 位角范围内的破片总能量增益达241.7%；D-120° 战斗部在47.6° 方位角范围内的破片能量增益为232.6%。

图 9 不同型面宽度下破片能量密度和破片总能量随方位角变化

Figure 9. Variation of energy density and total energy of fragments with azimuthal angle at different profile widths

下载: 全尺寸图片幻灯片

3. 破片飞散区分布快速计算

为了快速得到D型战斗部在不同型面宽度和起爆模式下破片飞散区域，建立如图10所示的分析模型，图中装药半径为7 cm；O₁、O₂、O₃为起爆点，其中O₁位于装药最左端，O₃位于装药圆心，O₂位于O₁和O₃之间；直线段破片编号从下向上依次为1， 2，…，11，其中A处对应破片编号9；θ₂、θ₃分别为A处爆轰波传播方向和破片飞散方向与对称轴O₁O₃的夹角，爆距d定义为起爆点到破片所在平面的垂直距离。

图 10 D型战斗部破片飞散区快速计算分析模型

Figure 10. Analysis model of rapid calculation of fragment force field of D-shaped fragmentation warhead

下载: 全尺寸图片幻灯片

对O₁、O₂、O₃三种起爆模式下的破片飞散特性进行数值模拟，由于对称位置的破片在起爆后沿水平方向飞散，边界处破片受侧向稀疏波作用飞散方向随机性较大，仅分析图中编号1～11的破片。得到各破片初始位置θ₂值以及对应角度θ₃的数值模拟结果如表1所示。

表 1 不同起爆模式下破片飞散特性

Table 1. Dispersion characteristic of fragment in different detonation modes

O₁点起爆			O₂点起爆			O₃点起爆
编号	sinθ₂	sinθ₃	编号	sinθ₂	sinθ₃	编号	sinθ₂	sinθ₃
1	0.046 62	0.006 64	1	0.069 83	0.006 37	1	0.138 65	0.008 71
2	0.092 93	0.013 19	2	0.138 65	0.015 38	2	0.269 63	0.019 75
3	0.138 65	0.020 16	3	0.205 52	0.022 61	3	0.387 23	0.027 43
4	0.183 5	0.028 69	4	0.269 63	0.030 86	4	0.488 6	0.034 72
5	0.227 23	0.036 57	5	0.330 35	0.040 54	5	0.573 46	0.042 65
6	0.269 63	0.050 11	6	0.387 23	0.054 03	6	0.643 19	0.052 04
7	0.310 52	0.062 52	7	0.440 02	0.076 77	7	0.699 93	0.064 89
8	0.349 75	0.073 69	8	0.488 6	0.088 97	8	0.745 94	0.083 76
9	0.387 23	0.095 91	9	0.533 04	0.105 17	9	0.783 29	0.110 5
10	0.422 89	0.117 78	10	0.573 46	0.132 98	10	0.813 73	0.142 42
11	0.456 68	0.150 4	11	0.610 09	0.166 94	11	0.838 69	0.172 66

下载: 导出CSV

| 显示表格

为了快速预测不同爆距d下的破片飞散分布情况，将爆距d与装药半径r的比值与表1中的sinθ₂、sinθ₃进行二次曲面拟合，拟合得到D-120°结构的破片分布快速计算公式：

$\sin {\theta _{3[{{120}^ \circ }]}} = - 0.5195{\rm{sin}}{\theta _{2[{{120}^ \circ }]}} - 0.0529\left( {d/r} \right) + 0.5137{\rm{si}}{{\rm{n}}^2}{\theta _{2[{{120}^ \circ }]}} - 0.0046{\left( {d/r} \right)^2} + 0.4048\left( {d/r} \right){\rm{sin}}{\theta _{2[{{120}^ \circ }]}} + 0.0822$

(1)

式中： ${\theta _{3[{{120}^ \circ }]}}$ 和 ${\theta _{2[{{120}^ \circ }]}}$ 分别为D-120° 结构的 ${\theta _3}$ 和 ${\theta _2}$ 。

为了验证拟合公式的准确性，将D-120° 结构装药半径调整为5 cm，分析在爆距6 cm和7.5 cm下的破片飞散结果。图11给出了两种爆距情况下数值模拟结果与公式(1)计算结果的对比图。结果表明，拟合的破片飞散区域公式与数值模拟结果吻合较好。

图 11 不同爆距下破片分布结果

Figure 11. Fragment distributions at different burst distances

下载: 全尺寸图片幻灯片

对D-90° 和D-150° 结构采用同样的方式进行拟合，得到破片分布快速计算公式：

${\rm{sin}}{\theta _{3[{{90}^ \circ }]}} = - 0.5085{\rm{sin}}{\theta _{2[{{90}^ \circ }]}} - 0.0692\left( {d/r} \right) + 0.5342{\sin ^2}{\theta _{2[{{90}^ \circ }]}}{\rm{ + }}0.0056{\left( {d/r} \right)^2} + 0.439\left( {d/r} \right)\sin {\theta _{2[{{90}^ \circ }]}} + 0.0811$

(2)

${\rm{sin}}{\theta _{3[{{150}^ \circ }]}} = - 0.53\sin {\theta _{2[{{150}^ \circ }]}} - 0.0575\left( {d/r} \right) + 0.5272{\sin ^2}{\theta _{2[{{150}^ \circ }]}} - 0.0039{\left( {d/r} \right)^2} + 0.3939\left( {d/r} \right)\sin {\theta _{2[{{150}^ \circ }]}} + 0.0853$

(3)

对于其他型面宽度D型战斗部，可以根据已有的三个拟合关系式，将对应工况的破片飞散状态进行计算，再通过构造二次插值函数来获得所求结构的破片空间分布数据，其他型面宽度对应的破片分布快速计算公式为：

$\begin{split} \sin {\theta _{3[x]}} =& \frac{{\left( {x - 120^\circ } \right)\left( {x - 150^\circ } \right)}}{{\left( {90^\circ - 120^\circ } \right)\left( {90^\circ - 150^\circ } \right)}}\sin {\theta _{3\left[ {90^\circ } \right]}} + \frac{{\left( {x - 90^\circ } \right)\left( {x - 150^\circ } \right)}}{{\left( {120^\circ - 90^\circ } \right)\left( {120^\circ - 150^\circ } \right)}}\sin {\theta _{3\left[ {120^\circ } \right]}} +\\& \frac{{\left( {x - 90^\circ } \right)\left( {x - 120^\circ } \right)}}{{\left( {150^\circ - 90^\circ } \right)\left( {150^\circ - 120^\circ } \right)}}\sin {\theta _{3\left[ {150^\circ } \right]}}\end{split}$

(4)

式中：x为D型面宽度对应的圆心角。

针对型面宽度105° 的D型战斗部，在装药半径5 cm，爆距7.5 cm情况下，将x=105° 代入公式（4），即可快速计算型面宽度105° 下破片分布结果，两种方法得到的sinθ₃结果如图12所示。利用构造二次插值函数得到的破片飞散角度与数值模拟结果吻合较好，因此通过构造二次插值函数来计算其他型面的破片分布是可行的。采用此方法可为不同型面宽度的D型战斗部破片分布快速计算提供一种途径。

图 12 D-105°战斗部破片飞散区快速计算结果

Figure 12. Rapid calculation of fragment force field of D-105° fragmentation warhead

下载: 全尺寸图片幻灯片

4. 结　论

（1）对三种型面宽度的D型战斗部破片飞散过程进行了实验和数值模拟研究，数值模拟结果与实验吻合较好，检验了材料模型和数值模拟方法的可靠性。

（2）偏心线起爆和双端面偏心起爆为D型战斗部的较优起爆方式，在目标方向上的能量聚焦能力强；型面宽度120° 的D型战斗部在这两种起爆方式下，20° 方位角内破片总能量分别是周向均匀战斗部中心起爆能量的3.4倍和3.3倍。

（3）D型战斗部型面宽度在90°～120° 之间时，目标方向能量增益较为明显。端面偏心起爆情况下，D-90° 结构在43.2° 方位角范围内的破片总能量与周向均匀结构相比增益达241.7%；D-120° 结构在47.6° 方位角范围内的破片能量增益为232.6%。

（4）为了快速分析D型战斗部的破片分布，基于三种典型型面的拟合公式，通过构建二次插值函数来快速求解其他D型战斗部破片飞散区，为D型战斗部对目标的快速评估提供了一种有效方法。

图 1 D型战斗部结构示意图

Figure 1. Illustration of D-shaped warheads

下载: 全尺寸图片幻灯片

图 2 弹靶布置图

Figure 2. Layout of warhead and target

下载: 全尺寸图片幻灯片

图 3 破片密度分布和破片数比例随方位角变化图

Figure 3. Variation of fragment density distribution and fragment ratio with azimuthal angle

下载: 全尺寸图片幻灯片

图 4 破片着靶高速摄影照片及破片速度结果

Figure 4. High-speed photography of the target and the experimental results of fragment velocity

下载: 全尺寸图片幻灯片

图 5 D型战斗部有限元模型

Figure 5. Finite element model of D-shaped warhead

下载: 全尺寸图片幻灯片

图 6 三种D型战斗部破片分布结果

Figure 6. Fragment distributions of three D-shaped warheads

下载: 全尺寸图片幻灯片

图 7 三种D型战斗部破片速度的实验和数值模拟结果

Figure 7. Fragment velocities of two D-shaped warheads

下载: 全尺寸图片幻灯片

图 8 不同起爆方式下破片能量分布

Figure 8. Fragment energy distribution in different denotation modes

下载: 全尺寸图片幻灯片

图 9 不同型面宽度下破片能量密度和破片总能量随方位角变化

Figure 9. Variation of energy density and total energy of fragments with azimuthal angle at different profile widths

下载: 全尺寸图片幻灯片

图 10 D型战斗部破片飞散区快速计算分析模型

Figure 10. Analysis model of rapid calculation of fragment force field of D-shaped fragmentation warhead

下载: 全尺寸图片幻灯片

图 11 不同爆距下破片分布结果

Figure 11. Fragment distributions at different burst distances

下载: 全尺寸图片幻灯片

图 12 D-105°战斗部破片飞散区快速计算结果

Figure 12. Rapid calculation of fragment force field of D-105° fragmentation warhead

下载: 全尺寸图片幻灯片

表 1 不同起爆模式下破片飞散特性

Table 1. Dispersion characteristic of fragment in different detonation modes

O₁点起爆			O₂点起爆			O₃点起爆
编号	sinθ₂	sinθ₃	编号	sinθ₂	sinθ₃	编号	sinθ₂	sinθ₃
1	0.046 62	0.006 64	1	0.069 83	0.006 37	1	0.138 65	0.008 71
2	0.092 93	0.013 19	2	0.138 65	0.015 38	2	0.269 63	0.019 75
3	0.138 65	0.020 16	3	0.205 52	0.022 61	3	0.387 23	0.027 43
4	0.183 5	0.028 69	4	0.269 63	0.030 86	4	0.488 6	0.034 72
5	0.227 23	0.036 57	5	0.330 35	0.040 54	5	0.573 46	0.042 65
6	0.269 63	0.050 11	6	0.387 23	0.054 03	6	0.643 19	0.052 04
7	0.310 52	0.062 52	7	0.440 02	0.076 77	7	0.699 93	0.064 89
8	0.349 75	0.073 69	8	0.488 6	0.088 97	8	0.745 94	0.083 76
9	0.387 23	0.095 91	9	0.533 04	0.105 17	9	0.783 29	0.110 5
10	0.422 89	0.117 78	10	0.573 46	0.132 98	10	0.813 73	0.142 42
11	0.456 68	0.150 4	11	0.610 09	0.166 94	11	0.838 69	0.172 66

下载: 导出CSV

参考文献(12)

[1]	LLOYD R M. Conventional warhead systems physics and engineering design [M]. Washington: The American Institute of Aeronautics and Astronautics, 1998: 193−243.
[2]	KENNEDY D R. A retrospective of the past years of warhead research and development—the pre- and present computer model era [C] // 19th International Symposium of Ballistics. Interlaken, Switzerland, 2001: 631−638.
[3]	SAM W. Relative performance of anti-air missile warheads [C] // 19th international Symposium on Ballistics. Interlaken, Switzerland, 2001: 623−630.
[4]	WANG M F, LU F Y, LI X Y, et al. A formula for calculating the velocities of fragments from velocity enhanced warhead [J]. Propellants, Explosives, Pyrotechnics, 2013, 38(2): 232–237. DOI: 10.1002/prep.201200025.
[5]	王力, 韩峰, 陈放, 等. 偏心对称起爆战斗部破片初速的增益 [J]. 爆炸与冲击, 2016, 36(1): 69–74. DOI: 10.11883/1001-1455(2016)01-0069-06 WANG Li, HAN Feng, CHEN Fang, et al. Fragments velocity of eccentric warhead with double symmetric detonators [J]. Explosion and Shock Waves, 2016, 36(1): 69–74. DOI: 10.11883/1001-1455(2016)01-0069-06
[6]	龚柏林, 卢芳云, 李翔宇. D型预制破片战斗部破片飞散过程的数值模拟 [J]. 弹箭与制导学报, 2010, 30(1): 88–90 doi: 10.3969/j.issn.1673-9728.2010.01.027 GONG Bolin, LU Fangyun, LI Xiangyu. Simulation and study on the fragment ejection process of premade D-shape warhead [J]. Journal of Projectile, Rockets, Missiles and Guidance, 2010, 30(1): 88–90 doi: 10.3969/j.issn.1673-9728.2010.01.027
[7]	王马法, 卢芳云, 李翔宇, 等. 非轴对称结构约束下破片飞散特性的实验和仿真研究 [J]. 振动与冲击, 2016, 35(15): 122–126. DOI: 10.13465/j.cnki.jvs.2016.15.020 WANG Mafa, LU Fangyu, LI Xiangyu, et al. Test and simulation for dispersion properties of fragments from asymmetric structures [J]. Jounal of Vibration and Shock, 2016, 35(15): 122–126. DOI: 10.13465/j.cnki.jvs.2016.15.020
[8]	WANG Mafa, LU Fangyun, LI Xiangyu, et al. A new method to estimate the projection angles of fragments from a D-shape configuration [C] // International Conference of Applied Mechanics and Materials, 2013, 275: 122−127. DOI: 10.4028/www.scientific.net/AMM.275-277.122.
[9]	李振铎, 李翔宇, 卢芳云, 等. D字形预制破片战斗部破片能量分布特性研究 [J]. 弹箭与制导学报, 2016, 36(1): 55–58. DOI: 10.15892/j.cnki.djzdxb.2016.01.014 LI Zhenduo, LI Xiangyu, LU Fangyu, et al. Study on fragment energy distribution characteristics of premade D-shape warhead [J]. Journal of Projectile, Rockets, Missiles and Guidance, 2016, 36(1): 55–58. DOI: 10.15892/j.cnki.djzdxb.2016.01.014
[10]	黄广炎, 冯顺山, 刘沛清. 战斗部破片对目标打击迹线的计算方法 [J]. 爆炸与冲击, 2010, 30(4): 413–418. DOI: 10.15892/j.cnki.djzdxb.2016.01.014 H U A N G G u a n g y a n , F E N G S h u n s h a n , L I U P e i q i n g . A v i s u a l C ~ ( + + ) a n d M a t l a b - b a s e d c o m p u t a t i o n a l m e t h o d f o r s h o t - l i n e s o f w a r h e a d f r a g m e n t s t o a t a r g e t [ J ] . E x p l o s i o n a n d S h o c k W a v e s , 2 0 1 0 , 3 0 ( 4 ) : 4 1 3 – 4 1 8 . D O I :
[11]	ALESSANDRO T, GIANFILIPPO G, GABRIELE L, et al. Assessment of fragment projection hazard: probability distributions for the initial direction of fragments [J]. Journal of Hazardous Materials, 2014, 279: 418–427. doi: 10.1016/j.jhazmat.2014.07.034
[12]	QIAN L X, LIU T, ZHANG S Q, et al. Fragment shot-line model for air defence warhead [J]. Propellants Explosives Pyrotechnics, 2000, 22: 92–98.

施引文献

期刊类型引用(11)

1.	张璐，刘海鹏，刘彦，安骋远，王璐. 椭圆变截面侵爆战斗部破片飞散特性分析. 兵器装备工程学报. 2025(03): 137-144 . 百度学术
2.	李豪凯，冯昱祥，李元，索涛. 多点起爆下鼓形战斗部的威力特性. 爆炸与冲击. 2024(03): 40-51 . 本站查看
3.	邓宇轩，张先锋，刘闯，李鹏程，马正伟，刘子涵. 起爆方式对椭圆截面战斗部破片速度分布的影响. 爆炸与冲击. 2024(10): 98-112 . 本站查看
4.	耿恒恒，向召，沈飞，张广华，王丛，屈可朋，陈鹏万，刘睿. 类D形战斗部装药能量输出优化数值模拟研究. 兵器装备工程学报. 2023(08): 124-132 . 百度学术
5.	解文辉，乔立刚，徐全振，魏许昌. 椭圆截面战斗部破片飞散特性研究. 兵器装备工程学报. 2023(11): 196-202 . 百度学术
6.	邓宇轩，张先锋，冯可华，刘闯，杜宁，刘均伟，李鹏程. 椭圆截面战斗部爆炸驱动破片作用过程的数值模拟. 高压物理学报. 2022(02): 155-165 . 百度学术
7.	姜斌，沈波，薛再清，李国杰，乔良，辛春亮. 椭圆形截面杀伤战斗部破片初速分布特性研究. 兵器装备工程学报. 2022(03): 149-155 . 百度学术
8.	邓海，全嘉林，梁争峰. 偏心起爆对战斗部装药能量分配增益的影响. 爆炸与冲击. 2022(05): 3-15 . 本站查看
9.	刘星雨，战仁军，欧阳的华，李永利. 蒙特卡洛剖分投影法的爆震弹破片平均比动能评估. 国防科技大学学报. 2021(05): 107-116 . 百度学术
10.	刘星雨，战仁军，李永利. 基于有限元结果的爆震弹破片飞散模型及仿真. 计算机仿真. 2020(05): 1-4+34 . 百度学术
11.	王佳颖，刘星雨. 基于边长约束的凹域三角剖分求破片迎风面积. 兵器装备工程学报. 2020(09): 63-67 . 百度学术

其他类型引用(3)

资源附件(0)

访问统计

图(12) / 表(1)

计量

文章访问数: 5561
HTML全文浏览量: 2114
PDF下载量: 80
被引次数: 14

1. 实　验
1.1 实验装置及弹靶布置
1.2 实验结果及分析
2. 数值模拟
2.1 计算模型及材料参数
2.2 与实验结果对比
2.3 破片飞散规律及分析
3. 破片飞散区分布快速计算
4. 结　论

D型战斗部破片飞散性及威力场快速计算

doi: 10.11883/bzycj-2017-0420

作者简介: 李翔宇（1980－ ），男，博士，副教授，xiangyulee@nudt.edu.cn

计量

出版历程

Dispersion properties and rapid calculation of fragment force field of D-shaped fragmentation warhead

1. 实 验

1.1 实验装置及弹靶布置

1.2 实验结果及分析

2. 数值模拟

2.1 计算模型及材料参数

2.2 与实验结果对比

2.3 破片飞散规律及分析

3. 破片飞散区分布快速计算

4. 结 论

期刊类型引用(11)

其他类型引用(3)

计量

出版历程

目录

1. 实 验

1.1 实验装置及弹靶布置

1.2 实验结果及分析

2. 数值模拟

2.1 计算模型及材料参数

2.2 与实验结果对比

2.3 破片飞散规律及分析

3. 破片飞散区分布快速计算

4. 结 论

作者简介:
李翔宇（1980－），男，博士，副教授，xiangyulee@nudt.edu.cn

1. 实　验

4. 结　论

1. 实　验

4. 结　论