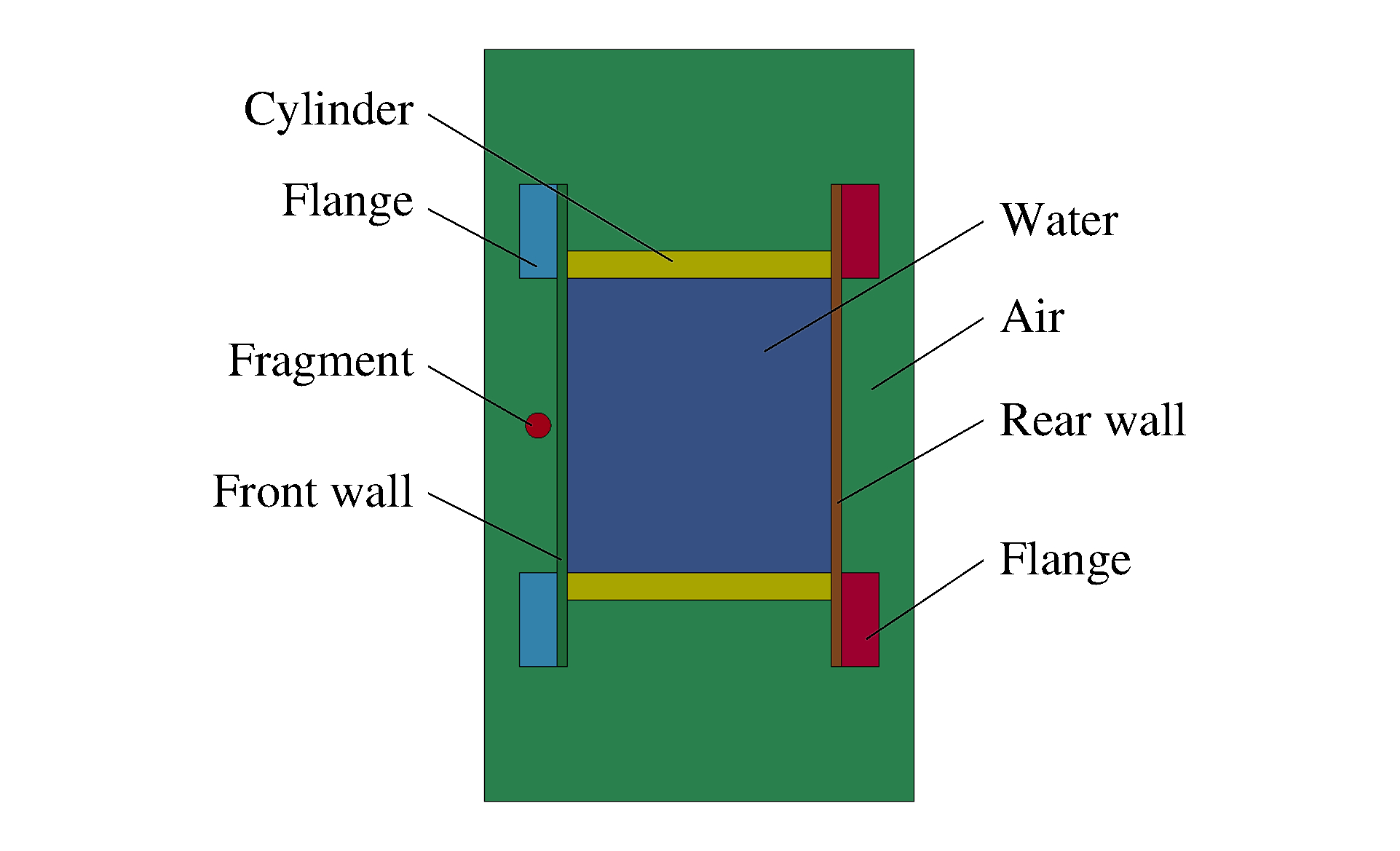
Study on wall damage of vessel in high-speed fragment impact liquid-filled vessel
-
摘要: 为研究高速破片(钨球)撞击充液容器(贯穿前后壁面)时容器壁面的毁伤情况,利用ANSYS/LS-DYNA对该过程进行了数值模拟,分析了破片撞击动能对充液容器前后壁面毁伤程度的影响,并进行实验验证。结果表明:高速破片撞击充液容器形成的液压水锤对充液容器前后壁面的破坏程度可分为3个等级,即前后壁面均未出现裂纹、前壁面没有出现裂纹后壁面出现裂纹和前后壁面均出现裂纹且后壁面呈花瓣式开裂;破片撞击充液容器过程中,前后壁面的最大变形量和前后壁面的裂纹总数随破片撞击动能的增加而增大。Abstract: We analyzed the influence of the impact energy on the damage degree of the front and rear walls and verified it by experiments. The results show that the hydrodynamic ram formed by a high-speed fragment impacting the liquid-filled vessel affects the vessel's front and rear walls and that the degree of the damage can be divided into three levels:the cracks are not observed on the front and rear walls; cracks are observed on the rear wall surface but on the front wall surface; cracks are observe on both front and rear walls and the rear wall is petal-type cracked. The maximum deformation of the front and rear walls and the total number of cracks in the front and rear walls increase with the increase of the impact energy of the fragments during the fragment impact process of the liquid-filled vessel.
-
Key words:
- ordnance science and technology /
- high speed fragment /
- liquid-filled vessel /
- hydrodynamic ram /
- wall damage /
- impact /
- damage
-
表 1 前后面板材料参数
Table 1. Material parameters of front and rear walls
材料 ρ/(kg·m-3) E/GPa μ A/MPa B/MPa C n m 铝2024-T4 2797 69.63 0.33 265 462 0.015 0.34 1.0 注:ρ-密度,E-弹性模量,μ-泊松比,A-屈服强度,B-应变硬化洗漱,C-应变率相关系数,n-应变硬化指数,m-温度相关系数. 表 2 Grüneisen状态方程参数
Table 2. Parameters of Grüneisen EOS
体积声速/(m·s-1) us-up曲线斜率 Grüneisen常数 5 286 1.4 2.0 表 3 破片材料参数
Table 3. Material parameters of fragment
材料 密度/(kg·m-3) 弹性模量/GPa 泊松比 钨 17 600 350 0.284 表 4 水和空气的主要材料参数表
Table 4. Material parameters of water and air
材料 密度/(kg·m-3) 体积声速/(m·s-1) us-up曲线斜率 C4 C5 水 1 000 1 480 1.979 - - 空气 1.25 - - 0.4 0.4 表 5 部分实验情况及结果表
Table 5. Part of the experimental situation and results
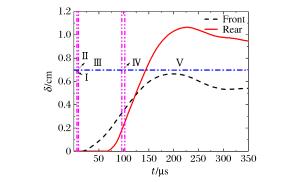
日期-发序 m/g v0/(m·s-1) vr/(m·s-1) E0/J δf/cm δr/cm 2016.12.23 -2 4.04 768 453 1 191.44 0.17 0.61 2016.12.23-3 4.03 1 049 699 2 217.31 0.48 0.98 2016.12.23-4 4.04 1 097 757 2 430.87 0.64 1.23 2016.12.23-5 4.01 1 399 933 3 924.19 0.68 2.87 2016.12.23-8 4.05 1 560 1 066 4 928.04 0.98 2.48 2017.03.26-1 8.10 1 028 755.8 4 279.98 0.69 2.69 2017.03.26-2 8.04 1 077.5 772.8 4 667.25 0.56 1.77 2017.03.26-3 8.14 1 026.7 740.1 4 290.24 0.59 21.9 2017.03.26-7 8.09 885.7 594.14 3 173.16 0.44 1.65 2017.03.26-8 8.08 1 130 808 5 158.68 0.70 3.14 2017.04.15-1 8.11 724.8 551.9 2 130.23 0.49 1.67 2017.04.15-2 8.06 1 238 948.1 6 176.56 1.19 4.12 2017.04.15-5 8.12 1 417 1 010 8 152.03 1.35 4.36 2017.04.15-6 8.11 1 554 1 082 9 792.48 1.31 4.07 注:m-破片质量,v0-破片撞击速度,vr-破片穿出容器后剩余速度,E0-破片撞击动能,δf-前壁面最大变形量,δr-后壁面最大变形量 表 6 试验与数值仿真中破片剩余速度对比
Table 6. Comparison of residual velocities in experiment and numerical simulation
日期-发序 E0/J vr/(m·s-1) 误差/% δf/cm 误差/% δr/cm 误差/% 实验 计算 实验 计算 实验 计算 2016.12.23-2 1 191 453 429 5.3 0.17 0.19 -11.76 0.61 0.66 -8.20 2017.03.26-2 4 667 772.8 761 1.4 0.56 0.63 -12.5 1.77 1.57 11.29 2017.04.15-6 9 792 1 082 1123.9 -3.9 1.31 1.29 1.5 4.07 3.49 14.25 -
[1] D'ALESSANDRO V. Modeling of tank vehicle dynamics by fluid sloshing coupled simulation[D]. Italy, 2012. https://www.politesi.polimi.it/handle/10589/56762 [2] LINGENFELTER A J, LIU D, REEDER M F. Time resolved flow field measurements of orifice entrainment during a hydrodynamic ram event[J]. Journal of Visualization, 2017, 20(1):63-74. DOI: 10.1007/s12650-016-0378-2. [3] FOUREST T, LAURENS J M, DELETOMBE E, et al. Confined Rayleigh-Plesset equation for hydrodynamic ram analysis in thin-walled containers under ballistic impacts[J]. Thin-Walled Structures, 2015, 86:67-72. DOI: 10.1016/j.tws.2014.10.003. [4] MOUSSA N A. The potential for fuel tank fire and hydrodynamic ram from uncontained aircraft engine debris: DOT/FAA/AR-96/95[R]. Springfield: National Technical Information Service, 1997. [5] BALL R E, POWER H L, FUHS A E. Fuel tank wall response to hydraulic ram during the shock phase[J]. Journal of Aircraft, 1973, 10(9):571-572. DOI: 10.2514/3.44393. [6] DISIMILE P J, DAVIS J, TOY N. Mitigation of shock waves within a liquid filled tank[J]. International Journal of Impact Engineering, 2011, 38(2):61-72. DOI: 10.1016/j.ijimpeng.2010.10.006. [7] CHARLES A, DELETOMBE E, DUPAS J. A numerical study on cavity expansion in water:hydraulic ram under ballistic impacts[J]. Structures Under Shock and Impact Ⅻ, 2013, 126:203. DOI: 10.2495/SU120181. [8] VARAS D, LÓPEZ-PUENTE J, ZAERA R. Numerical analysis of the hydrodynamic ram phenomenon in aircraft fuel tanks[J]. AIAA journal, 2012, 50(7):1621-1630. DOI: 10.2514/1.J051613. [9] VARAS D, LÓPEZ-PUENTE J, ZAERA R. Experimental analysis of fluid-filled aluminium tubes subjected to high-velocity impact[J]. International Journal of Impact Engineering, 2009, 36(1):81-91. DOI: 10.1016/j.ijimpeng.2008.04.006. [10] VARAS D, ZAERA R, LÓPEZ-PUENTE J. Numerical modelling of partially filled aircraft fuel tanks submitted to hydrodynamic ram[J]. Aerospace Science and technology, 2012, 16(1):19-28. DOI: 10.1016/j.ast.2011.02.003. [11] VARAS D, ZAERA R, LÓPEZ-PUENTE J. Numerical modelling of the hydrodynamic ram phenomenon[J]. International Journal of Impact Engineering, 2009, 36(3):363-374. DOI:10.1016/j.ijimpeng. 2008.07.020. [12] NISHIDA M, TANAKA K. Experimental study of perforation and cracking of water-filled aluminum tubes impacted by steel spheres[J]. International Journal of Impact Engineering, 2006, 32(12):2000-2016. DOI:10.1016/j.ijimpeng. 2005.06.010. [13] KWON Y W, YANG K, ADAMS C. Modeling and simulation of high-velocity projectile impact on storage tank[J]. Journal of Pressure Vessel Technology, 2016, 138(4):041303. DOI: 10.1115/1.4032447. [14] KWON Y, YUN K. Numerical parametric study of hydrodynamic ram[J]. International Journal of Multiphysics, 2017, 11(1):15-47. DOI: 10.21152/1750-9548.11.1.15. [15] 蒋运华, 徐胜利, 周杰.运动体小扰动下入水空泡试验研究[J].弹道学报, 2016, 28(1):81-86. DOI:10.3969/j.issn.1004-499X. 2016.01.015.JIANG Yunhua, XU Shengli, ZHOU Jie. Experimental study on water entry cavity for vehicle with small perturbation[J]. Journal of Ballistics, 2016, 28(1):81-86. DOI:10.3969/j.issn.1004-499X. 2016.01.015.issn. 1004-499X. 2016.01.015. [16] 张伟, 郭子涛, 肖新科, 等.弹体高速入水特性实验研究[J].爆炸与冲击, 2011, 31(6):579-584. doi: 10.11883/1001-1455(2011)06-0579-06ZHANG Wei, GUO Zitao, XIAO Xinke, et al. Experiment investigation on behaviors of projectile high-speed water entry[J]. Explosion and Shock Waves, 2011, 31(6):579-584. doi: 10.11883/1001-1455(2011)06-0579-06 [17] 郭子涛.弹体入水特性及不同介质中金属靶的抗侵彻性能研究[D].哈尔滨: 哈尔滨工业大学, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D241209 [18] 李典, 朱锡, 侯海量, 等.高速杆式弹体侵彻下蓄液结构载荷特性的有限元分析[J].爆炸与冲击, 2016, 36(1):1-8. DOI: 10.11883/1001-1455(2016)01-0001-08.LI Dian, ZHU Xi, HOU Hailiang, et al. Finite element analysis of load characteristic of liquid-filed structure subjected to high velocity long-rod projectile penetration[J]. Explosion and Shock Waves, 2016, 36(1):1-8. DOI: 10.11883/1001-1455(2016)01-0001-08. [19] 仲强, 侯海量, 朱锡, 等.陶瓷/液舱复合结构抗侵彻数值分析[J].爆炸与冲击, 2017, 37(3):510-519. DOI: 10.11883/1001-1455(2017)03-0510-10.ZHONG Qiang, HOU Hailiang, ZHU Xi, et al. Numerical analysis of penetration resistance of ceramic/fluid cabin composite structure[J]. Explosion and Shock Waves, 2017, 37(3):510-519. DOI: 10.11883/1001-1455(2017)03-0510-10. -







 下载:
下载: