Comparative studies on characteristics of elastic wave radiated
from the tamped explosion in loess and rock-like sandy soil
-
摘要: 研究地下爆炸弹性区的震动特性,关键是获得场地介质与爆炸能量耦合作用下辐射弹性波的实验参数。对于不易加工成大尺寸模型的砂土岩,为研究其填实爆炸下辐射弹性波的特征,采用0.125 g TNT微型炸药球作为爆炸源,以塑性区可置换的
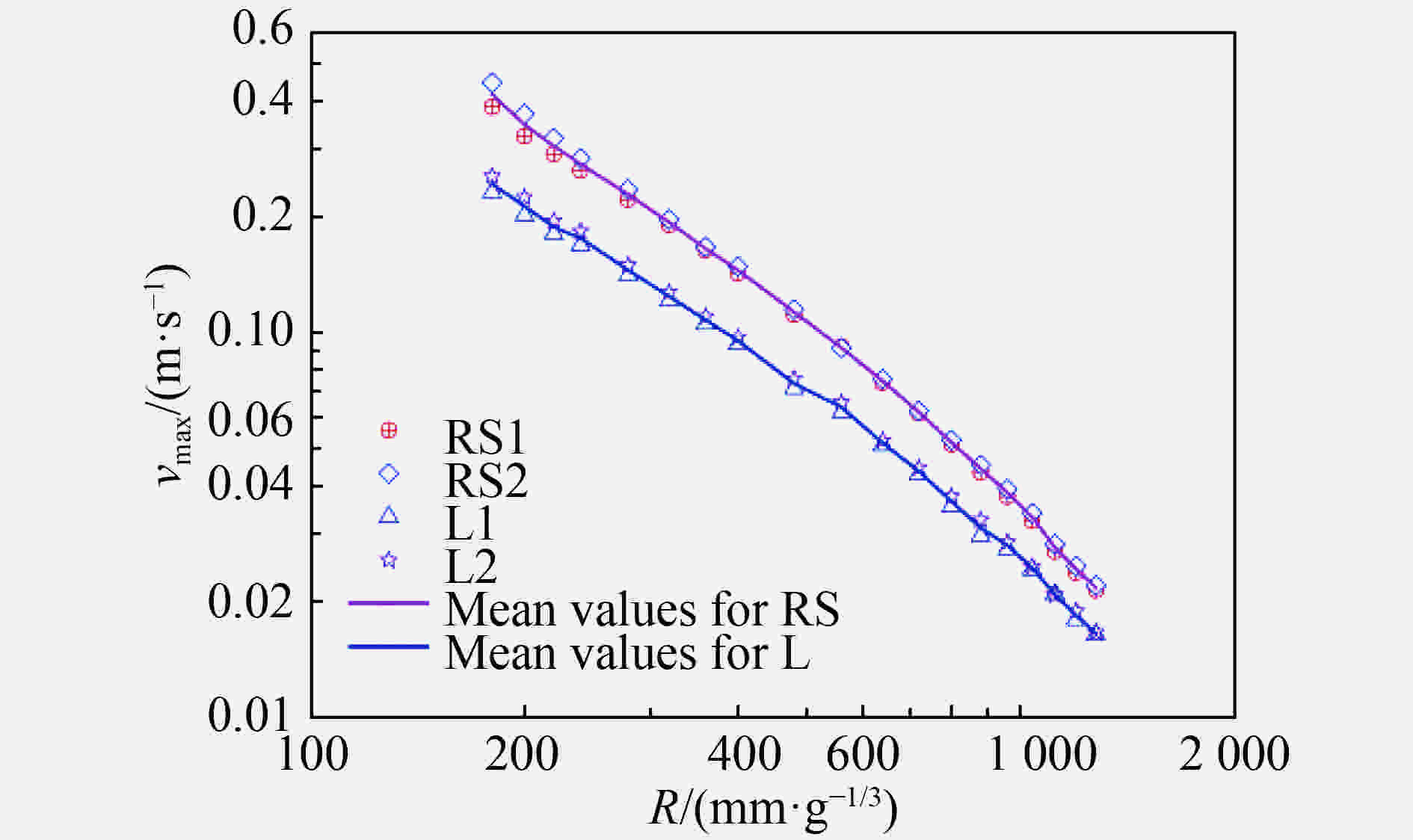
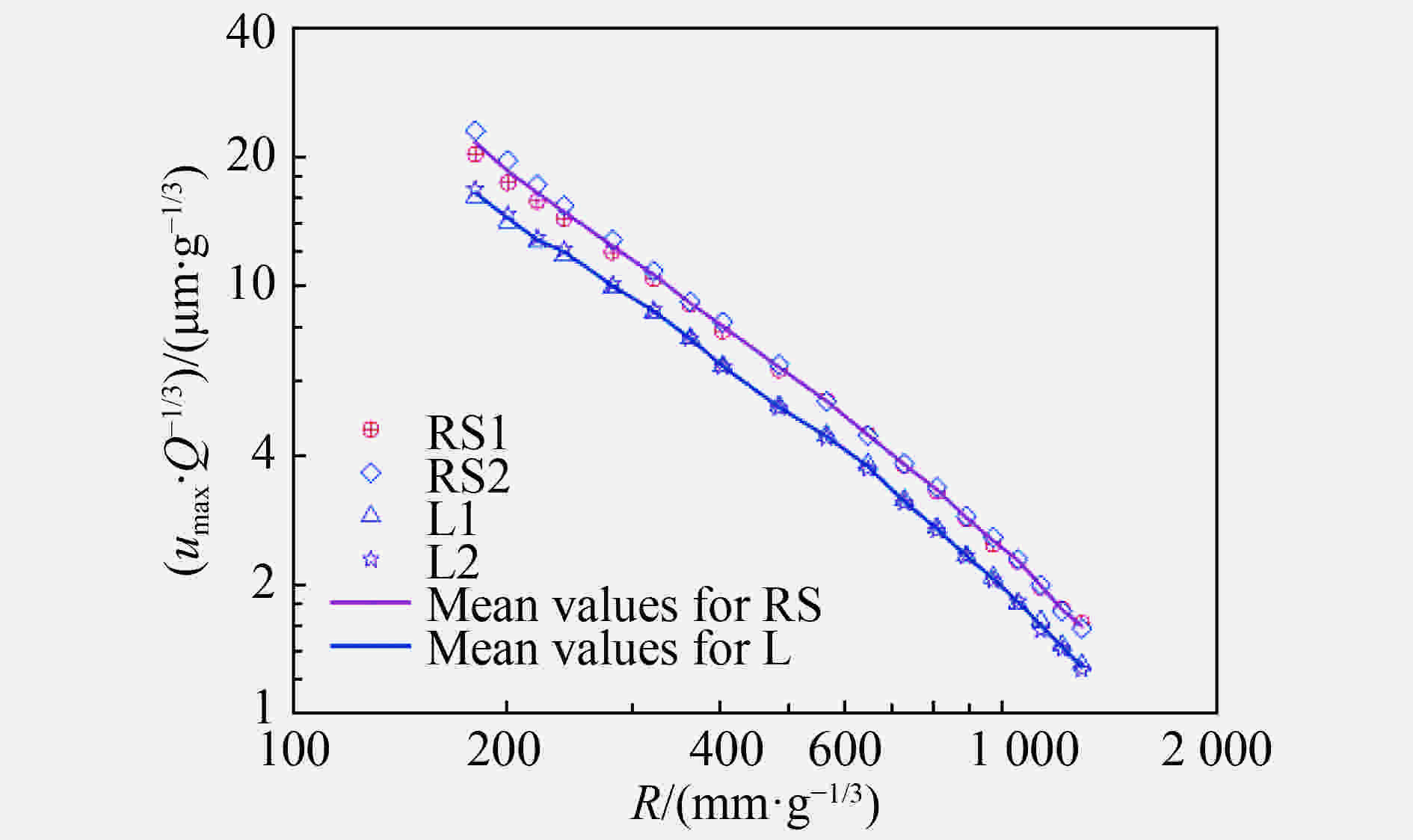
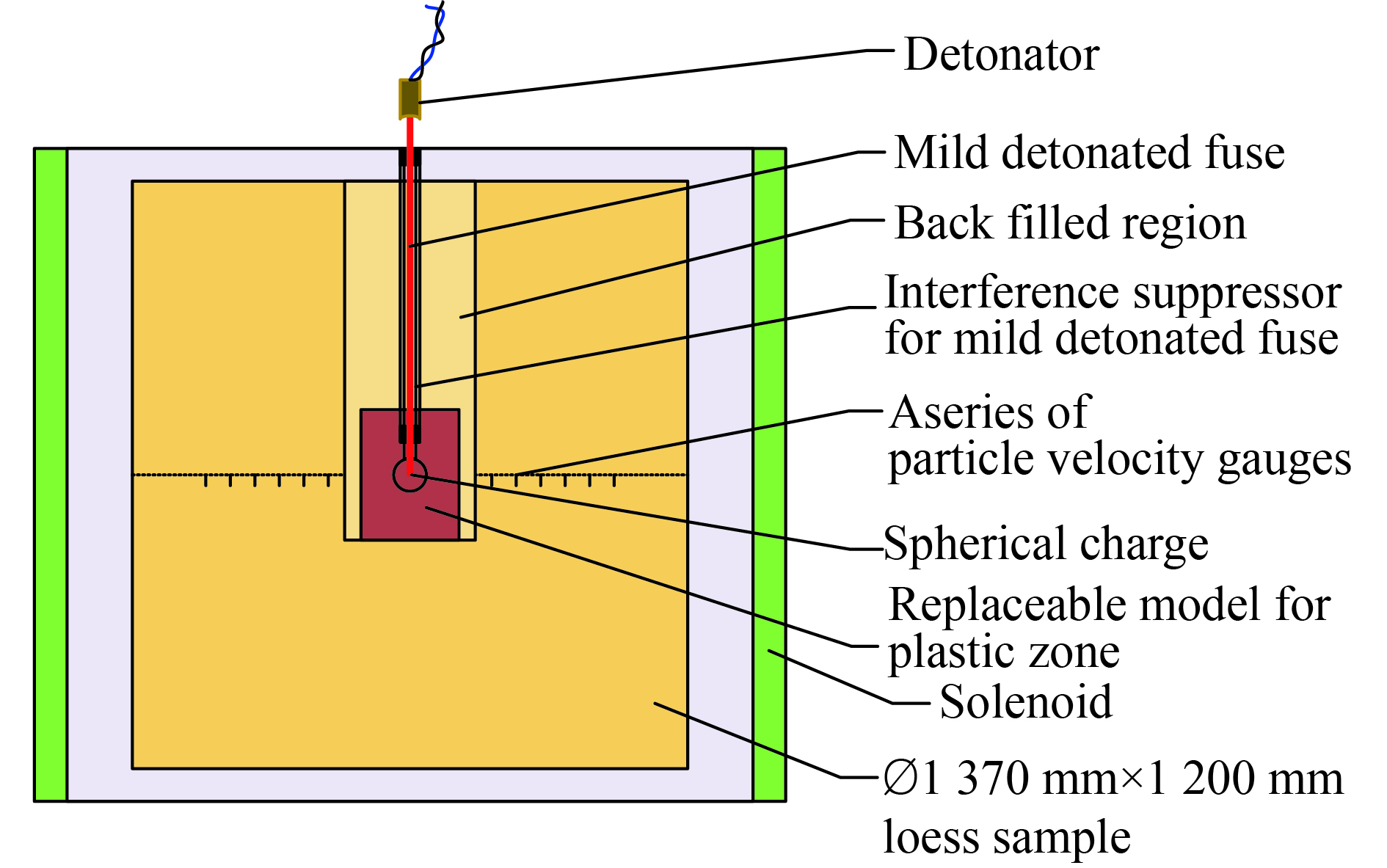
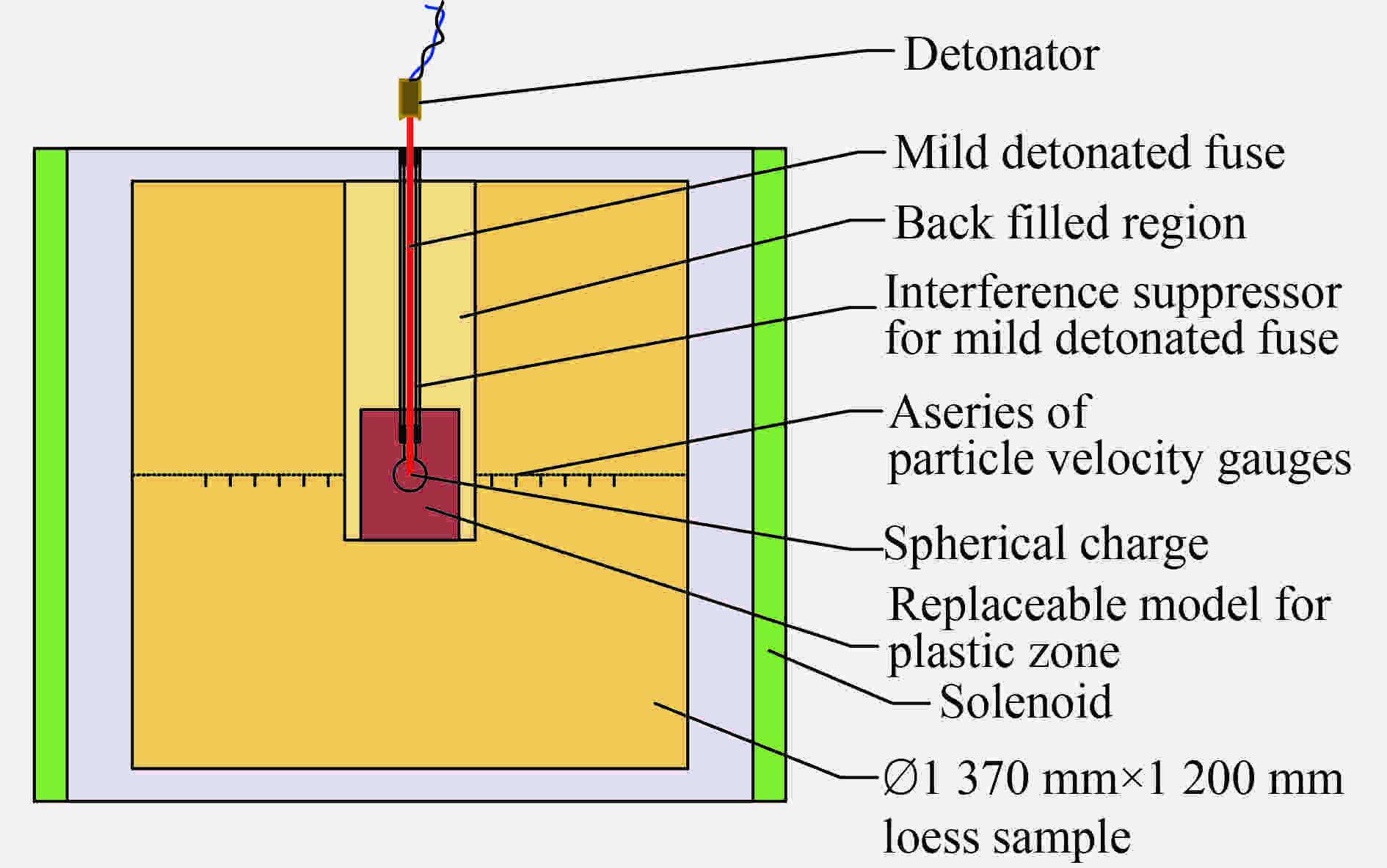
$\varnothing $ 1 370 mm×1 200 mm黄土样品作为提供应力波传播路径的载体,用波阻抗近似相等的重塑黄土和砂土岩样品分别作为源区介质,对比分析了两种介质中微药量填实爆炸辐射的弹性波传播特征。实验结果表明:在测试范围内,两种介质中填实爆炸激发的弹性应力波粒子速度(位移)峰值的衰减规律、波形的主频变化规律一致;砂土岩中爆炸辐射的弹性波粒子速度(位移)峰值整体高于黄土、粒子速度波形的半高宽和主频低于黄土;砂土岩中爆炸耦合的向外传播的弹性波能量比黄土大。实测结果反映,黄土和砂土岩中填实爆炸弹性波能量耦合强度的差别。Abstract: In order to study the vibration characteristics of the elastic zone of underground explosion, the key is to obtain the experimental parameters of the radiated elastic wave under the coupling of the site medium and the explosive energy. The rock-like sandy soil is not easily processed into large size model. To study the characteristics of the elastic wave radiated from the tamped explosion, a method was proposed by using 0.125 g TNT spherical charge as the explosive source and taking a$\varnothing $ 1 370 mm×1 200 mm loess sample with replaceable plastic-zone as a carrier for providing the propagation path. The characteristics of the elastic stress wave radiated from the tamped explosion in loess and rock-like sandy soil were investigated. The experimental results show that in the test range, the attenuation laws of the peak of the particle velocity (or displacement) and the variation for the dominant frequency of the particle velocity in the two media are consistent. The peak of the particle velocity (or displacement) for the elastic wave radiated from the tamped explosion in rock-like sandy soil is higher than that of loess, the full width at half maximum and the dominant frequency of the particle velocity are lower than that of loess. The coupling elastic wave energy between the tamped explosion and sandy soil is larger than that of loess. Measured results reflect the difference of elastic wave energy coupling strength of the tamped explosion in loess and sand rock explosion.-
Key words:
- underground explosion /
- elastic wave /
- particle velocity /
- attenuation of wave /
- loess /
- rock-like sandy /
- tamped explosion
-
表 1 黄土和砂土岩样品各成分组成(单位:%)
Table 1. Components of loess and rock-like sandy soil (unit: %)
材料 石英 石膏 方解石 绿泥石 蒙脱石 闪石 伊利石 白云石 斜长石 钾长石 赤铁矿 黄土 52 5 3 4 2 8 2 16 8 砂土岩 69 2 4 3 5 11 4 2 -
[1] 肖卫国, 王肖钧, 朱号锋, 等. 不同介质地下爆炸的地震耦合效应 [J]. 爆炸与冲击, 2012, 32(3): 267–272. DOI: 10.11883/1001-1455(2012)03-0267-06.XIAO Weiguo, WANG Xiaojun, ZHU Haofeng, et al. Experimental study on seismic coupling effects of underground explosions in different materials [J]. Explosion and Shock waves, 2012, 32(3): 267–272. DOI: 10.11883/1001-1455(2012)03-0267-06. [2] ANTOUN T H, VOROBIEV O Y, LOMOV I N. Simulations of an underground explosion in granite [C]// 11th Topical Conference on Shock Compression of Condensed Matter. Snowbird, Utah: American Physical Society, 1999. [3] PERRET W R. Free Field ground motion in granite: POR-4001[R]. Albuquerque, New Mexico: Sandia Laboratory, 1968. [4] 周钟, 王肖钧, 肖卫国, 等. 花岗岩介质中地下爆炸震源函数研究 [J]. 爆炸与冲击, 2007, 27(1): 18–25. doi: 10.11883/1001-1455(2007)01-018-08ZHOU Zhong, WANG Xiaojun, XIAO Weiguo, et al. Study on the main characteristics of underground explosion seismic source function in granite [J]. Explosion and Shock waves, 2007, 27(1): 18–25. doi: 10.11883/1001-1455(2007)01-018-08 [5] 周钟. 水饱和岩石本构模型和地下爆炸力学效应的数值研究[D]. 合肥: 中国科学技术大学, 2005. [6] 刘文韬, 王肖钧, 周钟. 岩石的连续损伤本构模型及其在地下爆炸波数值计算中的应用 [J]. 岩石力学与工程学报, 2004, 23(13): 2149–2156. doi: 10.3321/j.issn:1000-6915.2004.13.003LIU Wentao, WANG Xiaojun, ZHOU Zhong, et al. Continuously damaged constitutive model of rock and it s application to numerical simulation for underground strong explosion [J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2149–2156. doi: 10.3321/j.issn:1000-6915.2004.13.003 [7] LARSON D B. Spherical wave propagation in elastic media and its application to energy coupling for tamped and decoupled explosions: UCRL-52655(DE83013647)[R]. 1979. [8] RODEAN H C. Elastic wave radiation from spherical sources: UCRL-52867[R]. Lawrence Livermore Laboratory, 1979. [9] 赖华伟, 王占江, 杨黎明, 等. 线性黏弹性球面波的特征线分析 [J]. 爆炸与冲击, 2013, 33(1): 1–10. DOI: 10.11883/1001-1455(2013)01-01-010.LAI Huawei, WANG Zhanjiang, YANG Liming, et al. Characteristics analyses of linear viscoelastic spherical waves [J]. Explosion and Shock Waves, 2013, 33(1): 1–10. DOI: 10.11883/1001-1455(2013)01-01-010. [10] 赖华伟, 王占江, 杨黎明, 等. 由球面波径向质点速度实测数据反演材料黏弹性本构参数 [J]. 高压物理学报, 2013, 27(2): 245–252.LAI Huawei, WANG Zhanjiang, YANG Liming, et al. Inversion of constitutive parameters for viscoelastic materials from radial velocity measurements of spherical wave experiments [J]. Chinese Journal of High Pressure Physics, 2013, 27(2): 245–252. [11] WANG L L, LAI H W, WANG Z J, et al. Studies on nonlinear visco-elastic spherical waves by characteristics analyses and its application [J]. International Journal of Impact Engineering, 2013, 55: 1–10. doi: 10.1016/j.ijimpeng.2012.12.001 [12] LU Q, WANG Z J. Studies of the propagation of viscoelastic spherical divergent stress waves based on the generalized Maxwell model [J]. Journal of Sound and Vibration, 2016, 371(1): 183–195. [13] 卢强, 王占江, 丁洋, 等. 线黏弹性球面发散应力波的频率响应特性 [J]. 爆炸与冲击, 2017, 37(6): 1023–1030. DOI: 10.11883/1001-1455(2017)06-1023-08.LU Qiang, WANG Zhanjiang, DING Yang, et al. Characteristics of frequency response for linear viscoelastic spherical divergent stress waves [J]. Explosion and Shock waves, 2017, 37(6): 1023–1030. DOI: 10.11883/1001-1455(2017)06-1023-08. [14] 卢强, 王占江, 门朝举, 等. 塑性区沟槽对爆炸应力波屏蔽效应研究 [J]. 岩石力学与工程学报, 2013, 32(S1): 2642–2649.LU Qiang, WANG Zhanjiang, MEN Chaoju, et al. Study of shielding effects of gap in plastic zone on blasting stress wave [J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(S1): 2642–2649. [15] 王占江, 李孝兰, 张若棋, 等. 固体介质中球形发散波的实验装置 [J]. 爆炸与冲击, 2000, 20(2): 103–109. DOI: 10.11883/1001-1455(2000)02-0103-07.WANG Zhanjiang, LI Xiaolan, ZHANG Ruoqi, et al. An experimental apparatus for spherical wave propagation in solid [J]. Explosion and Shock Waves, 2000, 20(2): 103–109. DOI: 10.11883/1001-1455(2000)02-0103-07. [16] 王占江. 岩土中填实与空腔解耦爆炸的化爆模拟实验研究[D]. 长沙: 国防科技大学, 2003. -








 下载:
下载: