A Lagrangian inverse analysis technique for studying dynamic mechanical properites of brittle materials based on digital image correlation
-
摘要: 利用分离式Hopkinson压杆作为加载系统,借助超高速数字图像相关性分析方法,发展了长杆试件拉氏反分析实验技术,并用于研究脆性材料在小变形条件下的动态本构特性。通过超高速相机实时拍摄冲击加载下长杆试件变形的散斑图像,再对散斑图像进行数字图像相关性(digital image correlation,DIC)分析,获得长杆试件表面速度场和应变场。随后,以脆性材料PMMA(polymethyl methacrylate)为例,从DIC分析得到的速度场中提取出不同拉格朗日位置上质点速度时程曲线,构建路径线连接整个速度场,再结合零初始条件,数值求解得到了试件中的应力时程曲线,消去时间参数后,获得了脆性材料PMMA的动态应力-应变曲线,并与Hopkinson压杆实验和准静态压缩实验的结果进行了对比,揭示了PMMA材料在小应变条件下的黏弹性本构响应特征。Abstract: Based on the Hopkinson pressure bar and digital image correlation (DIC) techniques, a new Lagrangian inverse analysis experimental method was proposed to study the dynamic constitutive relation of brittle materials. A series of speckle images of long specimen deformation were recorded by an ultra-high-speed camera. The speckle images were processed by DIC to derive the velocity fields and strain fields on the surface of a long specimen. Based on the multi-particles velocity history curves measured by DIC, the whole velocity fields were constructed by many path lines. Then, a Lagrangian inverse analysis method was established for the dynamic constitutive relation of brittle rate-dependent PMMA materials by numerical solution. The results were compared with those of Hopkinson pressure bar test and quasi-static compression test, which display the characteristics of viscoelastic constitutive response of PMMA under the condition of small strain.
-
舰艇设计中,通常在舷侧设置空舱+液舱+空舱的组合防护结构,以提升其抗爆炸、抗冲击的性能。为实现舰艇设计的轻量化,一般仅在指挥中心、弹药库等关键舱室的舷侧设计抗爆抗冲击防护结构[1-2]。近年来,使用轻质高效的夹芯结构作为舷侧防护装甲成为舰船防护研究的热点。典型夹芯结构如图1所示,一般由两层面板和轻质芯体组成。应用夹芯结构,结构的质量并没有明显增加,但截面惯性矩有很大提升,是抗弯抗屈曲的较佳结构。负泊松比夹芯结构的力学特性取决于防护结构的材料特性、几何构型和宏观尺寸[3]。Mcshane等[4]研究了三种构型的夹芯梁结构在冲击载荷下的响应情况,研究表明,三种特殊构型的夹芯防护结构的抗冲击性能均相比传统的单层防护结构更优。Abrate[5]从理论上推导了爆炸冲击波作用下,防护结构的初始动响应,为仿真模型的构建提供了参考。Vasilache等[6]分析了爆炸当量、板厚和距爆心的远近等因素对夹芯结构抗爆防护效果的影响。姚熊亮等[7]分析了水下爆炸载荷下传统单层钢板和多层钢夹层板的动力学响应过程,分析显示,钢夹层板在抗变形能力和吸能方面较普通钢板具有很大优势。卢天健等[8]对比分析了等质量的泡沫铝夹芯圆筒与传统钢制圆筒的抗爆性能,分析表明,夹芯圆筒相比等质量的实体圆筒具有更优的能量吸收特性。邹广平等[9]研究了以硬质聚氨酯泡沫作为芯体的钢面板夹芯结构抗爆性能,并与相同面密度的钢板进行对比,结果表明,加入聚氨酯芯体后,结构的吸收能量为相同面密度钢板的1.49倍,结构抗爆性能得到较大提高。方岱宁等[10]探讨了金字塔形点阵金属材料夹芯结构抗爆性能。Avachat等[11]通过实验证明了复合材料夹芯圆筒的水下抗爆性能远胜于等质量实体圆柱筒。
杨德庆等[12-14]提出内六角型宏观负泊松比超材料舷侧防护结构,通过数值仿真,对负泊松比内六角型夹芯防护结构的抗冲击性能,以及水下爆炸冲击波作用下抗爆性能进行了研究,通过对内六角负泊松比蜂窝胞元构型的设计,研究负泊松比效应对防护性能的影响。本文在此基础上,对具有星型负泊松比夹芯的防护结构抗爆抗冲击性能进行研究,探讨星型负泊松比效应夹芯作为舷侧防护结构芯材的力学性能。
1. 星型负泊松比超材料夹芯防护结构
星型超材料防护结构具有特殊设计的负泊松比超材料芯层,能在受到爆炸冲击时吸收能量,减小破损或毁伤程度。本文通过数值仿真方法研究星型负泊松比夹芯防护结构的抗爆抗冲击性能、负泊松比超材料的结构参数对抗爆抗冲击性能的影响,并探讨防护结构的设计方法。
1.1 泊松比及弹性模量的解析表达式
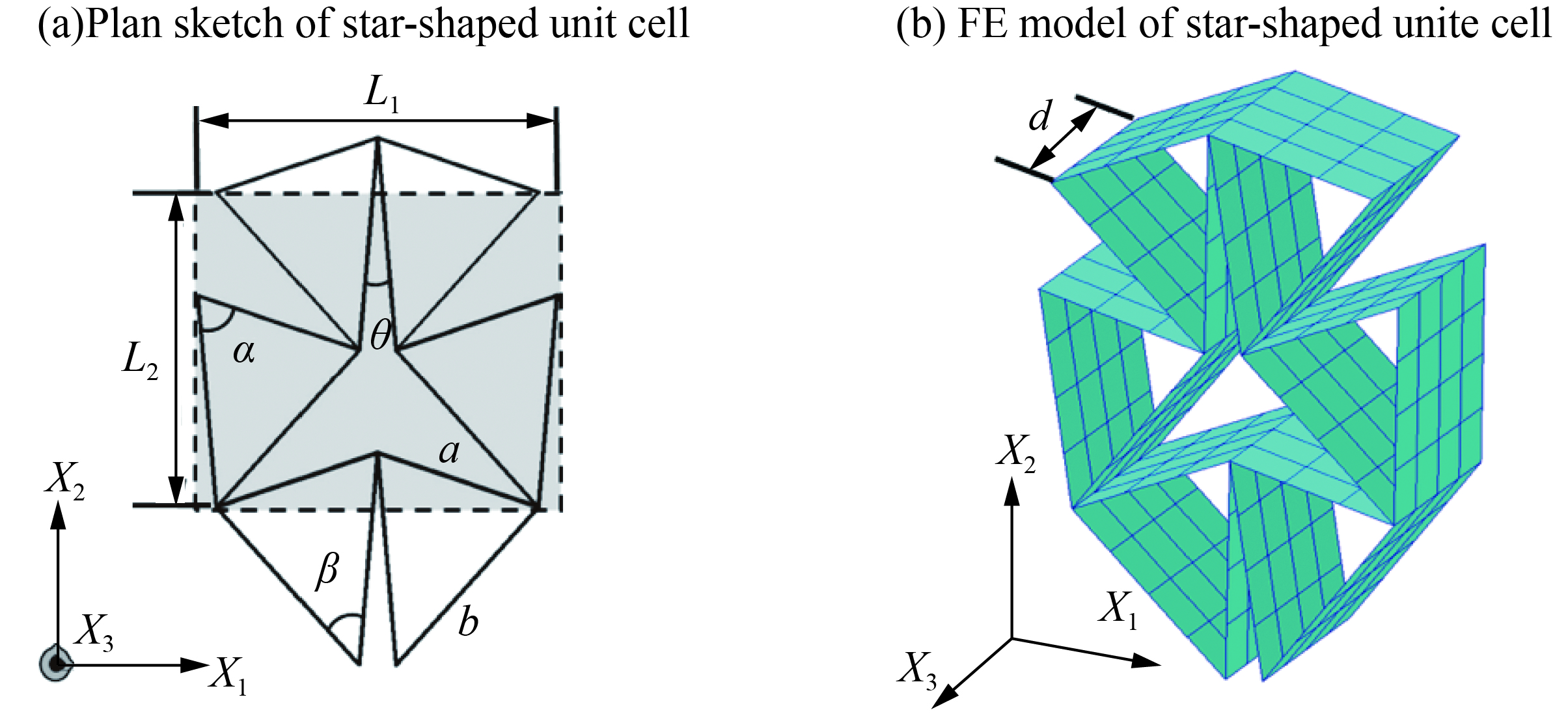
星型负泊松比超材料的胞元如图2所示,星型胞元由等腰三角形构成,其力学性质主要由胞元角θ和胞元形态比b/a决定。根据文献[15],星型多孔材料胞元泊松比
ν21 以及相对密度和ρ/ρs 为:ν21=ν−112=[bacos(α+θ2)+cos(θ2)]/[tan(2α+θ2)(basin(α+θ2)+sin(θ2))] (1) ρρs=(8a+4b)tL1⋅L2=[ta(2+ba)]/[[sinθ2+basin(θ2+α)]⋅cos(2α+θ2)] (2) 式中:
Es 、ρs 、t分别为胞元材料的杨氏模量、密度和胞元壁厚;L1、L2、α 、β 和γ 的定义如图2所示,具体的{α=acos(12⋅ba)β=π−(π−2α)−(π2−θ2)=2α+θ2−π2γ=12(π−2α−θ)=π2−(α+θ2) (3) 根据文献[16],星型多孔材料结构在X1与X2两个方向的弹性模量分别为:
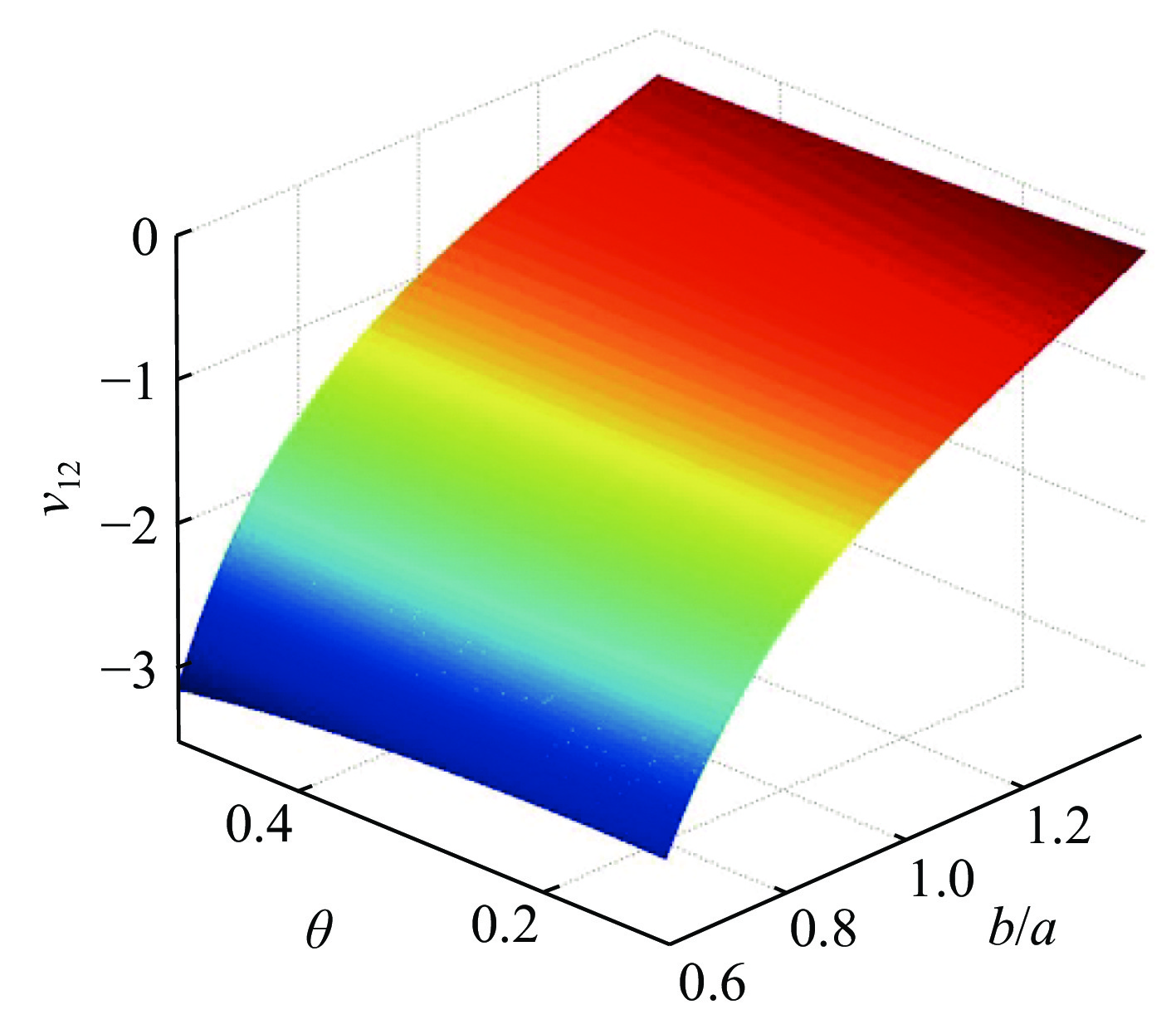
{E1=4Est(2+ba)(1+ν212)a(sinθ2+basin(θ2+α))(cosθ2−cos(2α+θ2)−bacos(α+θ2))E2=4Est(2+ba)(1+ν221)a(sinθ2+basin(θ2+α))(cosθ2−cos(2α+θ2)−vbacos(α+θ2)) (4) 本文分别采用泊松比为−2.91、−1.63、−1.00、−0.63的星型胞元设计夹芯防护结构。通过控制胞元角θ=10°,并使胞元形态比b/a在0.6~1.2变化来实现泊松比设计。图3是解析式(1)描述的泊松比依赖曲面。由图3可知,在一定范围内,星型负泊松比超材料的胞元泊松比随胞元形态比的增大而增大,随胞元角的增大而减小,泊松比对胞元形态比变化的响应更剧烈。
1.2 弹体冲击与水下爆炸计算模型
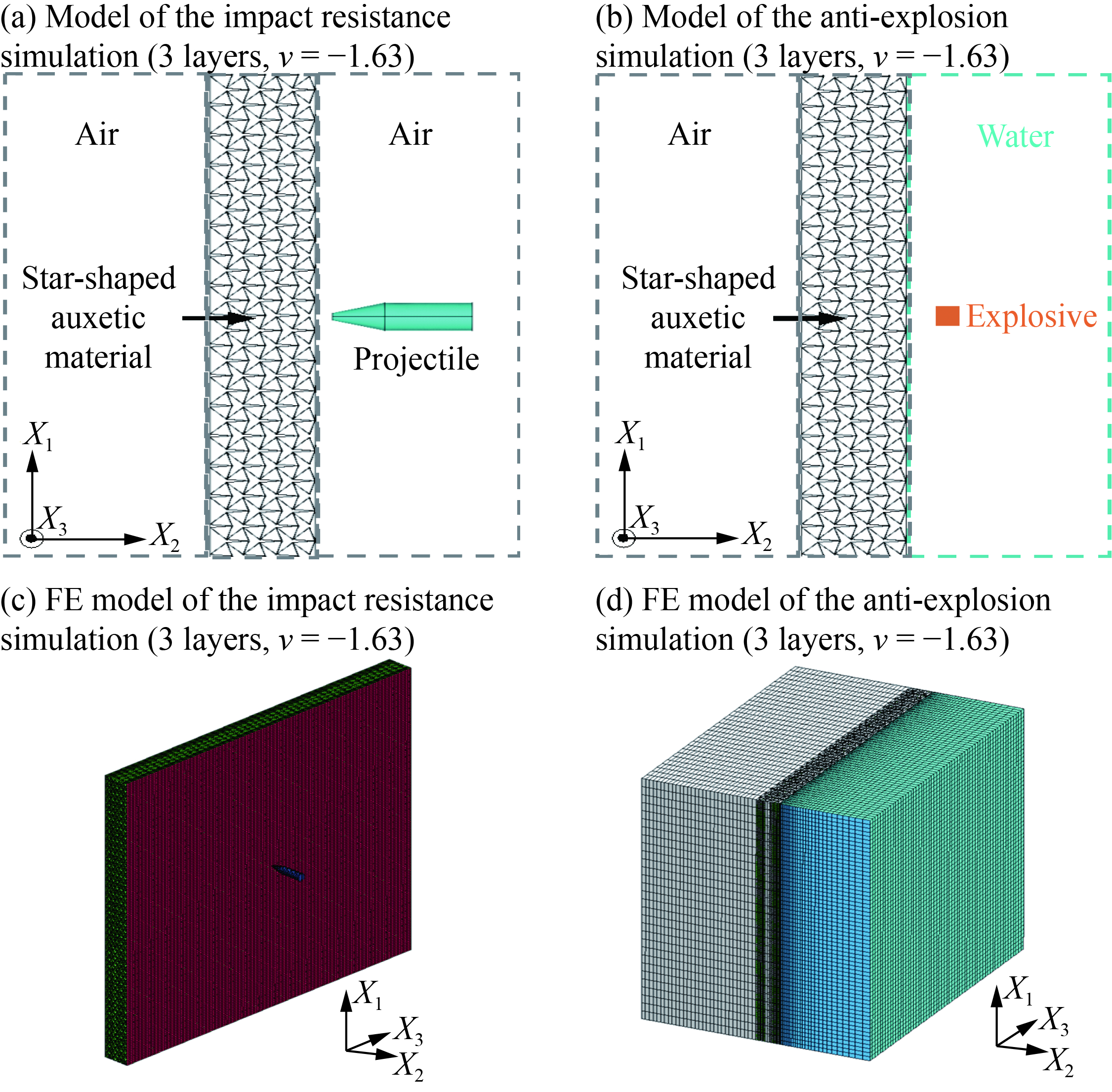
本文通过有限元程序ANSYS/LS-DYNA,对防护结构在弹体冲击载荷和水下爆炸冲击波载荷作用下的响应过程进行了数值仿真。计算模型示意图如图4所示。
研究中,计算模型的具体尺寸为:星型负泊松比夹芯防护结构的长度、宽度均为8.0 m,由两层钢面板和钢制星型负泊松比超材料芯层构成,两面板间距为600 mm。作为对照,常规的单层板防护模型采用等质量的长度和宽度均为8.0 m的单层钢制面板作为防护结构;等质量双层板采用长度和宽度均为8.0 m、相距600 mm的两块平行钢制面板组成防护结构。星型负泊松比夹芯结构分别采用泊松比ν为−2.91、−1.63、−1.00、−0.63的四种星型胞元,泊松比通过控制胞元角θ=10°,胞元形态比b/a在0.6~1.2之间变化实现。
针对每一泊松比,建立两种不同胞元层数的模型,分别为3层模型和5层模型。作为对照,常规的单层板、双层板防护结构模型长、宽均为8 m,双层板模型中两平行面板间距600 mm。各模型均采用四边简支约束,防护结构前后面板和芯层胞元均选取Shell 163单元模拟、焊接连接。有限元网格尺寸为2.0 mm×2.5 mm,前后面板与芯层负泊松比结构之间采用Automatic面-面接触,芯层结构本身星型负泊松比胞元壁之间采用Automatic单面接触。弹体冲击过程中弹体为截锥形穿甲弹,弹体截顶直径50 mm,弹体直径200 mm,长度800 mm,半锥角20°。分别设置弹体垂直入射初速度为200 m/s和340 m/s,入射点位于防护结构中心。水下爆炸仿真中,初始条件下,炸药位于距离防护结构面板200 mm处,炸药当量设定为10 kg。如图4(d)所示,水体尺寸为8.0 m×8.0 m×2.4 m,位于夹芯防护结构右侧,采用越近邻夹芯防护结构外侧面板网格尺寸越细致的27 000个Solid 164单元模拟。夹芯防护结构内部填充空气层,尺寸与夹芯防护结构尺寸一致,为8.0 m×8.0 m×0.6 m,由30×30×10=9 000个Solid 164模拟。夹芯防护结构右侧为另一空气层,尺寸为8.0 m×8.0 m×3.0 m,由30×30×30=27 000个Solid 164单元模拟。
1.3 状态方程与材料属性
计算中弹体材料取为刚体,密度为7 820 kg/m3。水的状态方程采用Grüneisen方程:
p=ρ0c2μ[1+(1−γ02)μ−α2μ2][1−(S1−1)μ−S2μ2μ+1−S3μ3(μ+1)2]2+(γ0+αμ)E (5) 式中:p为压强;密度
ρ0 =103 kg/m3;水下声速c=1 484 m/s;材料系数S1=1.979,S2=0,S3=0,γ0=0.11 ,α=3.0 ;相对体积V=1.0;单位体积内能E=3.072×105 Pa。空气的状态方程采用线性多项式方程:
p=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E (6) 式中:材料常数C0~C3均为0,C4=C5=0.4,C6=0,E=2.5×105 Pa,空气密度为1.28 kg/m3。
炸药采用JWL状态方程和MAT_HIGH_EXPLOSIVE_BURN材料模型:
P=A(1−ωR1v)e−R1V+B(1−ωR2v)e−R2V+ωEv (7) 式中:v=6 930 m/s为爆速,A=371.2 GPa,B=3.23 GPa,R1=4.15,R2=0.95,
ω =0.30,E=9.60 GPa为材料系数。防护结构设计材料为45钢,采用Johnson-Cook本构模型,流动应力描述为:
σy=(A1+B1ˉεnp)(1+Cln˙ε∗)(1−T∗m) (8) 式中:A1、B1、C、n和m都是材料输入常数;
ˉεp 为等效塑性应变;˙ε∗ 是˙ε0=1 s−1时有效塑性应变率,˙ε∗=˙ˉεp/˙ε0 ,˙ˉεp 为实验中的应变率,˙ε0 为参考应变率;T∗ 为相对温度,T∗=(T−T0)/(Tm−T0) ,Tm为材料融化温度,T0为室温破坏应变定义为:
εf=[D1+D2exp(D3σ∗)](1+D4ln˙ε∗)(1+D5T∗) (11) σ∗ 为压力与有效压力之比,σ∗=p/σeff ;D1~D5为断裂常量,当破坏参数D达到1时即认为发生断裂:D=∑(Δˉεp/εf) (13) 数值模拟中,水与结构间流固耦合计算选用ALE算法,计算网格不依附于流体质点,可以相对于坐标系作任意运动。45钢材料参数如表1所示。
表 1 材料参数Table 1. Material parameters材料性质参数 Johnson-Cook本构模型参数 Johnson-Cook失效模型参数 E/GPa ν ρ/(kg·m−3) Tm/K T0/K A/MPa B/MPa C n m D1 D2 D3 D4 D5 200 0.2 7 820 1 783 293 507 320 0.064 0.28 1.06 0.1 0.76 1.57 0.005 −0.84 2. 抗弹体冲击性能分析
2.1 常规结构抗冲击性能
为对比分析星型负泊松比超材料夹芯防护结构的抗爆抗冲击性能,本文建立了等质量的传统单层、双层钢板防护结构数值模型,进行相同载荷的爆炸冲击模拟。传统防护结构的材料与夹芯防护结构选取的材料一致。单层防护结构钢板厚50 mm,双层防护结构前后钢板厚度均为25 mm,两面板距离600 mm。弹体冲击过程模拟示意图如图5~6所示,冲击计算结果如图7~10所示。
由图7~8可知,入射初速度为200 m/s和340 m/s的弹体穿透传统单层防护结构后的剩余速度为114 m/s和288 m/s。由图9~10可知,入射初速度为200 m/s和340 m/s的弹体穿透传统双层防护结构后的剩余速度分别为151 m/s和310 m/s。对比可知,相同弹速入射初速度下,单层防护结构的抗冲击性能优于等质量的双层防护结构。此数值结果与图11中展示的Teng和Durmus等试验结果一致,证明了本文数值方法的准确性[17-18]。
2.2 等质量前提下星型负泊松比夹芯防护结构抗冲击性能
为探究星型负泊松比夹芯防护结构的抗弹体冲击性能,本文设定星型防护结构的总质量与单层钢板防护结构相同,靠近弹体的面板厚度为20 mm,远离弹体的面板厚度为10 mm。表2展示了相同质量前提下,不同胞元层数、不同胞元泊松比的防护结构芯层对应的胞元壁厚。夹芯防护结构在弹体冲击载荷下的仿真计算剩余速度如图12~13所示。
表 2 防护结构芯层胞元壁厚Table 2. Cell thickness of Sandwich defensive structure胞元层数 3层 5层 泊松比 −2.91 −1.63 −1.00 −0.63 −2.91 −1.63 −1.00 −0.63 胞元壁厚/mm 0.87 1.01 1.16 1.68 0.54 0.60 0.65 0.97 由表2可知,等质量情况下,超材料夹芯防护结构芯层的胞元层数越少,泊松比对弹体剩余速度的影响越小。当夹芯防护结构胞元层数为5层时,随胞元泊松比的增大,弹体剩余速度先减小后增大,在泊松比为−1.63时取得极小值。此外,当胞元泊松比较小时,弹体穿过5层胞元夹芯防护结构后的剩余速度相比穿过3层胞元夹芯防护结构更低。
与单层、双层钢板防护结构的抗冲击模拟结果对比可知,等质量夹芯防护结构不具有明显的穿甲防护性能。这是因为弹体入射速度很高,负泊松比胞元未能充分形变就已经被破坏、穿透,压阻效应无法展现。图13展示了夹芯层受弹体高速冲击时大塑性变形和破坏的典型细观截面图像:弹体直接穿透了面板和芯层,冲击力作用范围小,星型负泊松比超材料芯层的塑性形变和破坏仅局限在弹道附件极小范围内。负泊松比蜂窝通过本身薄壁结构在压阻效应下的形变和破坏来吸收并耗散机械能,在高速弹体冲击下应力波还没有充足的时间传递至打击点周围的蜂窝胞元,弹体便已经穿透夹芯层。因此星型结构未能充分发挥其吸能耗能的作用,吸收或耗散足够的弹体运动的机械能。在质量相等的情况下,星型负泊松比超材料芯层的几何构型使弹体侵彻路径上的穿透的防护结构质量相比单层钢板更小,因此穿过星型负泊松比夹芯防护结构的弹体剩余速度相比单层钢板更高。
3. 水下抗爆模拟
3.1 单层、双层防护结构水下爆炸过程模拟
单层防护结构水下爆炸过程仿真结果如图14所示,单层钢板厚170 mm,钢板设置四边简支。等质量的双层防护结构水下爆炸过程仿真结果如图15所示,前后两钢板厚度均为85 mm,两板相距600 mm。为更好地与下文中等质量星型负泊松比超材料防护结构的抗爆响应作对比,本文还分别模拟了迎爆面钢板厚度20 mm、背爆面钢板厚度150 mm(将芯层星型负泊松比结构的质量附加至背爆面钢板),两板相距600 mm的双层板防护结构;以及迎爆面钢板厚度150 mm、背爆面钢板厚度20 mm(将芯层星型负泊松比结构的质量附加至迎爆面钢板),两板相距600 mm的双层板防护结构的水下抗爆过程。根据数值计算,四类常规的钢板防护结构在爆炸载荷下的最大破口尺寸及最大塑性区域尺寸如表3所示。
表 3 X1方向最大破口尺寸及塑性区域尺寸Table 3. Maximum fracture region size and plastic region size防护结构 最大破口尺寸/cm 最大塑性区域尺寸/cm 破口与塑性应变区比值 单层板防护结构 62.68 605.26 0.104 等质量双层板防护结构背爆面(前后面板厚度一致) 143.68 263.94 0.544 等质量双层板防护结构背爆面(迎爆面钢板厚度 20 mm) 83.53 249.96 0.334 等质量双层板防护结构背爆面(背爆面钢板厚度 20 mm) 127.18 240.03 0.530 根据图14~15,传统防护结构在水下爆炸载荷下X1方向与X3方向的破口和塑性变形区域尺寸基本一致。根据表3,将质量较为集中地分配在一侧面板(迎爆面钢板厚度20 mm模型或背爆面钢板厚度20 mm模型),其背爆面最大破口尺寸相比前后钢板厚度一致的双层板防护结构更小。此外,三种不同质量分配模式的双层板防护结构的背爆面最大破口尺寸皆相比单层板防护结构的最大破口尺寸更大。
3.2 等质量条件下超材料夹芯防护结构水下爆炸仿真
设定夹芯防护结构的前后面板厚度均为20 mm,控制夹芯防护结构总质量与3.1中所述传统防护结构总质量相同,如此计算出各模型的星型负泊松比超材料芯层胞元壁厚如表4所示。爆炸造成的星型负泊松比夹芯防护结构前后面板破口尺寸与塑性应变区域尺寸如图16~17所示。
表 4 等质量条件下芯层胞元壁厚Table 4. Cell thickness of sandwich defensive structure under condition of equal mass胞元层数 3层 5层 泊松比 −2.91 −1.63 −1.00 −0.63 −2.91 −1.63 −1.00 −0.63 胞元壁厚/mm 5.66 6.56 7.54 10.92 3.51 3.90 4.23 6.31 根据图16,三层星型负泊松比夹芯结构的前后面板破口尺寸随泊松比的增大先减小后增大,泊松比为−1.00时迎爆面面板破口尺寸最小,泊松比为−1.63时,背爆面面板破口尺寸最小,为35.8 mm。迎爆面面板破口尺寸与背爆面面板破口尺寸负相关,即迎爆面面板破口尺寸越大,背爆面面板破口尺寸越小。这是因为爆炸产生的总能量是一定的,迎爆面钢板与负泊松比芯层破坏越严重,它们吸收的能量越多,传递到背爆面面板的能量便越低,对背爆面钢板造成的破坏越弱。根据图17,塑性区域尺寸随泊松比的变化与最大破口尺寸随泊松比的变化基本一致。
等质量条件下星型负泊松比结构水下抗爆仿真结果如图18所示。爆炸造成的迎爆面面板破口与塑性应变区比值如图19所示。
根据图18及图19,等质量的夹芯防护结构在抗爆仿真过程中,迎爆面产生塑性大变形和相对较小的破坏区域,负泊松比芯层被大范围压缩、形变和破坏。由于负泊松比压阻效应,受压后的星型负泊松比结构向爆炸冲击波冲击中心收缩,局部密度增大,整个防护结构尚未被爆炸冲击波完全穿透。
图20展示了截面上负泊松比芯层受水下爆炸载荷时产生大塑性变形、破坏的典型细观过程。图19中星型夹芯结构迎爆面破口与塑性应变区比值明显大于单层板防护结构,由于破坏结构所需的能量相比使结构产生塑性应所需的能量更高,因此星型负泊松比夹芯结构相比单层板具有更高的能量吸收效率。
3.3 等壁厚条件下星型负泊松比夹芯结构水下抗爆仿真分析
为进一步探明星型胞元壁厚对水下抗爆性能的影响,对上述四种泊松比的3层、5层防护结构模型分别在胞元壁厚为5、10、15 mm时的抗爆过程进行数值仿真,计算结果如图21所示。
根据图21,胞元壁厚对星型夹芯防护结构的抗爆性能有显著的影响,整体上看厚度越大,星型夹芯防护结构的抗爆性能越好。胞元泊松比为−1.00,胞元层数为3层时,胞元壁厚5 mm的夹芯结构被炸穿,产生较大破口;胞元壁厚15 mm的夹芯结构则未被完全炸穿,背爆面基本保全完好。这是因为夹芯层厚度越大,破坏芯层所需的能量越多,传递至背爆面的冲击波所携带的能量约少。
根据数值计算,等壁厚条件下,爆炸造成的星型负泊松比夹芯防护结构前后两侧面板破口尺寸与塑性应变区域尺寸如图22~23所示。
由图22~23可知,星型夹芯防护结构前后面板塑性区域最大尺寸变化趋势与最大破口尺寸变化趋势基本一致。对3层星型夹芯防护结构,随着泊松比从−0.63~−2.91增大,背爆面的最大破口尺寸先减小后增大,泊松比−1.63与−1.00时取得极小值。对5层胞元夹芯结构,胞元壁厚10 mm时背爆面破口随泊松比的增大先减小后增大,在−1.63处取得极小值;胞元壁厚15 mm时,泊松比对背爆面最大破口尺寸影响不明显:均在40 cm上下波动。星型胞元壁厚的增大总体上会使背爆面破口尺寸减小,这是因为胞元壁厚的增大使得毁坏夹芯层所需消耗的能量更多,导致传递至背爆面的冲击波得到了相应的缓解。
等壁厚条件下5层胞元结构虽然相比3层胞元结构有更大的相对密度,但同时胞元层数的增加也增大了星型夹芯结构的整体刚度,造成芯层变形能力减弱,压阻效应受到影响。星型胞元层数为3层、胞元壁厚15 mm、泊松比−1.63和−1.00的星型负泊松比夹芯防护结构背爆面完整,没有受到破坏。
4. 结 论
本文通过数值仿真研究了星型负泊松比超材料夹芯防护结构的胞元层数、泊松比以及胞元壁厚对其抗爆抗冲击性能的影响,主要结论如下:(1) 星型负泊松比夹芯结构的抗冲击性能与传统防护结构类似,均无法抵挡高速弹体冲击;这主要是由于弹体冲击速度过高,星型结构不能快速形变并传递弹体冲击带来的能量,压阻效应无法体现;(2) 等质量前提下,合理设计的星型负泊松比夹芯防护结构抗爆性能相比常规单层板防护结构更优;负泊松比材料的压阻效应在抗爆过程中得到展现,破口面积与塑性区域面积的比值明显大于常规防护结构,芯层的能量吸收耗散效率更高;泊松比的变化对抗爆仿真计算结果影响明显,层数3层、泊松比−1.63的星型夹芯结构的能量吸收率高,背爆面破口尺寸最小;(3) 等壁厚前提下,3层星型负泊松比夹芯防护结构总体上相比5层防护结构抗爆性能更优;5层胞元防护结构增大了夹芯层的整体刚度,造成芯层变形能力减弱,压阻效应受到影响,对爆炸冲击能量的吸收相应减弱;(4) 综合考虑星型负泊松比夹芯防护结构芯层的胞元层数、泊松比和壁厚,设计中建议使用3层、泊松比−1.63的星型胞元,在此基础上根据设计需求选取胞元壁厚;此类星型胞元在等质量、等壁厚前提下均表现出较好的抗爆性能,且在等壁厚条件下相对密度相比相同泊松比的5层星型胞元更低,防护结构总质量更轻,加工难度低,更适合实际工程应用。
-
[1] 王礼立, 王永刚.应力波在用SHPB研究材料动态本构特性中的重要作用[J].爆炸与冲击, 2005, 25(1):17-25. doi: 10.3321/j.issn:1001-1455.2005.01.004WANG Lili, WANG Yonggang. The important role of stress wave in the study on dynamic constitutive behavior of materials by SHPB[J]. Explosion and Shock Waves, 2005, 25(1):17-25. doi: 10.3321/j.issn:1001-1455.2005.01.004 [2] 王礼立, 朱珏, 赖华伟.冲击动力学研究中实测波信息的解读分析[J].高压物理学报, 2010, 24(4):279-285. http://d.old.wanfangdata.com.cn/Conference/6414825WANG Lili, ZHU Jue, LAI Huawei. Understanding and interpreting of the measured wave signals in impact dynamics studies[J]. Chinese Journal of High Pressure Physics, 2010, 24(4):279-285. http://d.old.wanfangdata.com.cn/Conference/6414825 [3] FOWLES R. Conservation relations for spherical and cylindrical stress waves[J]. Journal of Applied Physics, 1970, 41:2740-2741. doi: 10.1063/1.1659298 [4] GRADY D E. Experimental analysis of spherical wave propagation[J]. Journal of Geophysical Research, 1973, 78:1299-1307. doi: 10.1029/JB078i008p01299 [5] SEAMAN L. Lagrangian analysis for multiple stress or velocity gages in attenuating waves[J]. Journal of Applied Physics, 1974, 45:4303-4314. doi: 10.1063/1.1663050 [6] 唐志平.Lagrange分析方法及其新进展[J].力学进展, 1993, 23(3):348-359. doi: 10.3321/j.issn:1000-0992.1993.03.007TANG Zhiping. Lagrangian analysis and its recent developments[J]. Advances in Mechanics, 1993, 23(3):348-359. doi: 10.3321/j.issn:1000-0992.1993.03.007 [7] 陈叶青, 冯叔瑜.拉格朗日分析方法研究现状及应用中应注意的问题[J].爆炸与冲击, 1998, 18(1):91-96. http://www.bzycj.cn/CN/abstract/abstract10386.shtmlCHEN Yeqing, FENG Shuyu. Present conditions of Lagrangian analysis and problems should be consided in the use[J]. Explosion and Shock Waves, 1998, 18(1):91-96. http://www.bzycj.cn/CN/abstract/abstract10386.shtml [8] 陶为俊, 浣石, 蒋国平.基于最小二乘法的Lagrange分析方法研究[J].振动与冲击, 2012, 31(12):98-101. http://d.old.wanfangdata.com.cn/Periodical/zdycj201221020TAO Weijun, HUAN Shi, JIANG Guoping. Lagrangian analysis method based on least square[J]. Journal of Vibration and Shock, 2012, 31(12):98-101. http://d.old.wanfangdata.com.cn/Periodical/zdycj201221020 [9] 陶为俊, 浣石.沿时间逐步求解应力的拉格朗日分析方法研究[J].物理学报, 2012, 20:200703. doi: 10.7498/aps.61.200703TAO Weijun, HUAN Shi. Study on Lagrangian analysis for solving the stress gradually along the time[J]. Acta Physica Sinica, 2012, 20:200703. doi: 10.7498/aps.61.200703 [10] 林英睿, 王占江, 李运良, 等.依球面波粒子速度研究材料的本构关系[J].解放军理工大学学报(自然科学版), 2007, 8(6):606-610. http://d.old.wanfangdata.com.cn/Periodical/jfjlgdxxb200706009LIN Yingrui, WANG Zhanjiang, LI Yunliang, et al. Constitutive relation using particle velocity data of spherical waves[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2007, 8(6):606-610. http://d.old.wanfangdata.com.cn/Periodical/jfjlgdxxb200706009 [11] WANG L, ZHU J, LAI H. A new method combining Lagrangian analysis with Hopkinson pressure bar technique[J]. Strain, 2011, 47:173-182. doi: 10.1111/str.2011.47.issue-2 [12] WANG Lili, DING Yuanyuan, YANG Liming. Experimental investigation on dynamic constitutive behavior of aluminum foams by new inverse methods from wave propagation measurements[J]. International Journal of Impact Engineering, 2013, 62:48-59. doi: 10.1016/j.ijimpeng.2013.06.002 [13] 丁圆圆, 杨黎明, 王礼立.对基于质点速度测量的拉格朗日分析法的进一步探讨[J].宁波大学学报(理工版), 2012, 25(4):83-87. http://d.old.wanfangdata.com.cn/Periodical/nbdxxb-lg201204019DING Yuanyuan, YANG Liming, WANG Lili. A further discussion on the lagrangian analysis method based on particle velocity wave profiles measurements[J]. Journal of Ningbo University (Natural Science and Engineering), 2012, 25(4):83-87. http://d.old.wanfangdata.com.cn/Periodical/nbdxxb-lg201204019 [14] DING Yuanyuan, WANG Shilong, ZHENG Zhijun, et al. Dynamic crushing of cellular materials:A unique dynamic stress-strain state curve[J]. Mechanics of Materials, 2016, 100:219-231. doi: 10.1016/j.mechmat.2016.07.001 [15] 蒋国平, 浣石, 郝洪, 等.钢纤维高强混凝土材料的气炮试验研究[J].物理学报, 2013, 62(1):016201. http://d.old.wanfangdata.com.cn/Periodical/wlxb201301052JIANG Guoping, HUAN Shi, HAO Hong, et al. Performance of steel reinforced high strength concrete investigated in the gas gun experiment[J]. Acta Physica Sinica, 2013, 62(1):016201. http://d.old.wanfangdata.com.cn/Periodical/wlxb201301052 [16] 张磊, 胡时胜, 梁宗宪.利用拉氏分析研究冲击载荷下混凝土应力-应变曲线[J].工程力学, 2005, 22(4):163-166. doi: 10.3969/j.issn.1000-4750.2005.04.030ZHANG Lei, HU Shisheng, LIANG Zongxian. Lagrange analysis of the stress-strain relation of concrete material under impact[J]. Engineering Mechanics, 2005, 22(4):163-166. doi: 10.3969/j.issn.1000-4750.2005.04.030 [17] 赖华伟, 王礼立.用改进的基于质点速度测量的拉格朗日分析方法研究尼龙动态力学特性[J].实验力学, 2011, 26(2):221-227. http://d.old.wanfangdata.com.cn/Periodical/sylx201102017LAI Huawei, WANG Lili. Nylon dynamic mechanical behavior study through a modified Lagrangian analysis based on particle velocity profile measurement[J]. Journal of Experimental Mechanics, 2011, 26(2):221-227. http://d.old.wanfangdata.com.cn/Periodical/sylx201102017 [18] BARKER L M, HOLLENBACK R E. Laser interferometer for measuring high velocities of any reflecting surface[J]. Journal of Applied Physics, 1972, 43(11):4469-4675. https://www.researchgate.net/publication/224521486_Laser_Interferometer_for_Measuring_High_Velocities_of_Any_Reflecting_Surface [19] WENG Jidong, TAN Hua, HU Shaolou, et al. New all-fiber velocimeter[J]. Review of Scientific Instruments, 2005, 76(9):093301. doi: 10.1063/1.2008989 [20] WU Xianqian, WANG Xi, WEI Yanpeng, et al. An experimental method to measure dynamic stress-strain relationship of materials at high strain rates[J]. International Journal of Impact Engineering, 2014, 69(4):149-156. https://www.sciencedirect.com/science/article/pii/S0734743X14000554 [21] LEA L J, JARDINE A P. Application of photon Doppler velocimetry to direct impact Hopkinson pressure bars[J]. Review of Scientific Instruments, 2016, 87(2):023101. doi: 10.1063/1.4940935 [22] SUTTON M A, ORTEU J J, SCHREIER H. Image correlation for shape, motion and deformation measurements:Basic concepts, theory and applicants[M]. New York:Springer, 2009:81-116. [23] SATO K, YU Q, HIRAMOTO J, et al. A method to investigate strain rate effects on necking and fracture behaviors of advanced high-strength steels using digital imaging strain analysis[J]. International Journal of Impact Engineering, 2014, 75:11-26. https://www.sciencedirect.com/science/article/pii/S0734743X1400147X [24] LIU J, SALETTI D, PATTOFATTO S, et al. Impact testing of polymeric foam using Hopkinson bars and digital image analysis[J]. Polymer Testing, 2014, 36:101-109. doi: 10.1016/j.polymertesting.2014.03.014 [25] 申海艇, 蒋招绣, 王贝壳, 等.基于超高速相机的数字图像相关性全场应变分析在SHTB实验中的应用[J].爆炸与冲击, 2017, 37(1):15-20. http://www.bzycj.cn/CN/abstract/abstract9680.shtmlSHEN Haiting, JIANG Zhaoxiu, WANG Beike, et al. Full field strain measurement in split Hopkinson tension bar experiments by using ultra-high-speed camera with digital image correlation[J]. Explosion and Shock Waves, 2017, 37(1):15-20. http://www.bzycj.cn/CN/abstract/abstract9680.shtml [26] 刘剑飞, 胡时胜, 王道荣.用于脆性材料的Hopkinson压杆动态实验新方法[J].实验力学, 2001, 16(3):283-290. http://d.old.wanfangdata.com.cn/Periodical/sylx200103007LIU Jianfei, HU Shisheng, WANG Daorong. A novel experimental method of Hopkinson pressure bar system for brittle materials[J]. Journal of Experimental Mechanics, 2001, 16(1):283-290. http://d.old.wanfangdata.com.cn/Periodical/sylx200103007 期刊类型引用(21)
1. 刘磊,王共冬,刘辰泽,吕文为. 基于藤壶仿生超材料的综合防护性能研究. 包装工程. 2025(09): 286-295 .  百度学术
百度学术2. 贺锋,梁一鸣,秦海,李季,高超,刘三丰. 负泊松比结构的工程应用现状及展望. 防护工程. 2024(01): 68-78 .  百度学术
百度学术3. 蒋舟顺,徐峰祥,邹震,周谦谋. 爆炸载荷下正弦曲边三维负泊松比夹芯板的动态响应和吸能特性. 爆炸与冲击. 2024(02): 3-20 .  本站查看
本站查看4. 陈洋,王肇喜,翟师慧,盛鹏,王者蓝,朱明亮. 3D打印点阵夹芯结构冲击损伤的近场动力学模拟. 爆炸与冲击. 2024(03): 146-160 .  本站查看
本站查看5. 孔维凡,付涛. 负泊松比内凹六边形蜂窝夹层板的吸声性能. 复合材料学报. 2024(04): 2157-2166 .  百度学术
百度学术6. 黄绮雯,张慧华,韩尚宇,纪晓磊. 弧形负泊松比蜂窝结构抗冲击性能的有限元分析. 南昌航空大学学报(自然科学版). 2024(02): 76-88 .  百度学术
百度学术7. 贺锋,梁一鸣,李季,高超,慕孟,白家琦,祁少博. 异型陶瓷负泊松比复合结构的防弹防爆性能数值模拟研究. 安全与环境学报. 2024(08): 2919-2928 .  百度学术
百度学术8. 韩广,郄彦辉,班宝旺. 新型斜十字负泊松比结构弹性力学性能研究. 机械强度. 2023(01): 183-189 .  百度学术
百度学术9. 朱春晓,徐双喜,陈威,李晓彬,乐京霞. 负泊松比曲边内凹同心蜂窝结构冲击吸能特性研究. 武汉理工大学学报(交通科学与工程版). 2023(01): 90-95 .  百度学术
百度学术10. 刘洋佐,马大为,任杰,仲健林,赵昌方. 双箭头负泊松比结构抗侵彻性能. 国防科技大学学报. 2023(02): 197-207 .  百度学术
百度学术11. 张栗铭,杨德庆. 力学与声学超材料在船舶工程中的应用研究综述. 中国舰船研究. 2023(02): 1-19+47 .  百度学术
百度学术12. 崔天宁,秦庆华. 轻质多孔夹芯结构的弹道侵彻行为研究进展. 力学进展. 2023(02): 395-432 .  百度学术
百度学术13. 谢红胜,罗刚,袁坤. 一种偏转结构抗侵彻性能试验及数值仿真. 武汉理工大学学报(交通科学与工程版). 2023(04): 644-647+653 .  百度学术
百度学术14. 侯海量,王克,柴崧淋,李典,赵著杰. 水下接触爆炸下夹芯式防雷舱抗爆效能研究. 船舶力学. 2023(10): 1550-1561 .  百度学术
百度学术15. 崔飞蝶,董焱章,李青峰. 多型负泊松比材料-结构协同设计. 湖北汽车工业学院学报. 2023(04): 64-69+75 .  百度学术
百度学术16. 赵雨薇,张宏伟,孙晓旺,王显会. 爆炸载荷下负泊松比下肢保护装置参数分析. 兵器装备工程学报. 2022(03): 60-66+106 .  百度学术
百度学术17. 孙魁远,孙晓旺,张宏伟,王显会,彭兵,张绍彦. 厚度梯度型负泊松比蜂窝抗爆炸特性及优化. 兵器装备工程学报. 2022(04): 190-197 .  百度学术
百度学术18. 赵颖,王凯锋,施劲余,桑叶,李云伍,陈宇,殷举伞. 微元胞缺失下三星型微结构面内动态性能分析. 振动与冲击. 2022(10): 115-123+185 .  百度学术
百度学术19. 周辉,任辉启,吴祥云,易治,黄魁,穆朝民,王海露. 成层式防护结构中分散层研究综述. 爆炸与冲击. 2022(11): 3-28 .  本站查看
本站查看20. 孙晓旺,陶晓晓,王显会,李进军,王利辉. 负泊松比蜂窝材料抗爆炸特性及优化设计研究. 爆炸与冲击. 2020(09): 66-76 .  本站查看
本站查看21. 邓裕坤,梁学称,裴小鹏,翟侃侃,王超,张百超,白云刚,张文德,谭颖,王丕新,徐昆. 柔性主链的支化结构对冲击硬化材料性能的影响. 应用化学. 2019(10): 1155-1164 .  百度学术
百度学术其他类型引用(24)
-








 下载:
下载:




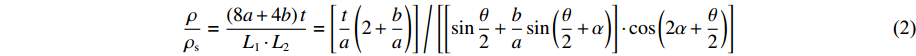





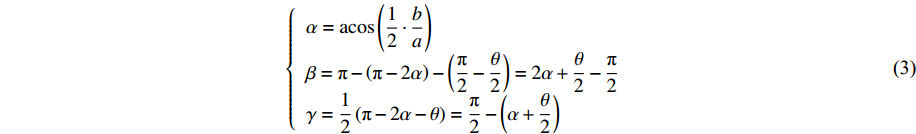









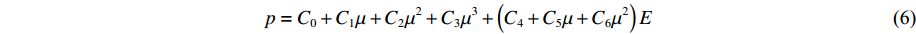
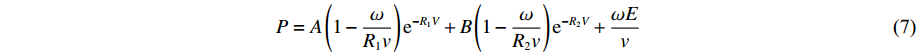










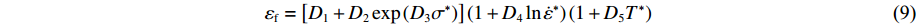






























 下载:
下载:


 百度学术
百度学术