Analysis on whole dynamical fracture process of tight sandstone tunnel model under impact loading
-
摘要: 为了开展在不同冲击载荷作用下巷道围岩内裂纹的起裂、扩展及止裂等问题，以可调速冲击试验机进行动态加载试验，采用致密青砂岩制作裂纹巷道模型试件，并利用裂纹扩展计分别记录了动态起裂、扩展、止裂等时刻，对裂纹扩展速度的变化规律进行分析；随后采用AUTODYN有限差分法软件进行相应的数值模拟，数值模拟得到的裂纹扩展路径与试验结果基本一致。经过两者对比分析可知：随着冲击载荷作用的增加，裂纹平均扩展速度逐渐增大，随后趋于稳定值；预制裂纹的起裂时间随着冲击速度载荷的增加而逐渐降低，并在稳定值上下波动；随着冲击速度载荷的增加，裂纹扩展路径过程中的止裂时段逐渐变短。Abstract: In order to investigate the properties of crack fracture time, propagation speed and arrest period in the surrounding rock of tunnel under different impact loading speed, the dynamic tests were performed by self-developed adjustable speed drop weight impact test system, and the tight green sandstone was selected to make the cracked tunnel specimens. A crack propagation gauge (CPG) was applied to measure dynamic initiation time, propagation speeds and arrest time, respectively. The properties of crack propagation velocity, crack fracture time and crack arrest period were discussed and analyzed. The corresponding numerical simulation was carried out by AUTODYN code, and the simulation results showed that the crack propagation speeds and crack fracture time generally agree with the experimental results, and crack arrest period also was calculated. The results show that crack propagation speeds increase with impact loading speed, but as the impact loading speed is larger than a certain value, the crack speeds tend toward a stable value; Crack fracture time decreases with the increase of impact loading speed, and as the loading rate is larger than a certain value, it tends toward a stable value; With the increase of the impact loading speed, the crack arrest period in the crack propagation path gradually decreases.
-
Key words:
- tunnel /
- impact loading /
- crack propagation speeds /
- crack fracture time /
- crack arrest time
-
在巷道爆破掘进过程中，围岩中存在大量的宏观裂隙和微观裂隙群，在动载荷作用下，会促使原生裂纹群的孕育、萌生、繁衍、扩展及贯通，使巷道围岩周围产生不同程度的破坏，最终导致巷道的失稳与坍塌。因此，冲击载荷作用下巷道围岩动态断裂问题是我国深部地下矿产资源开采亟需解决的重要研究课题。
巷道内围岩的破坏与剥落通常始于巷道围岩内岩石的初始裂纹与节理缺陷，裂纹在天然缺陷周边起裂、扩展、贯通进而导致破坏是岩石类脆性材料破坏的重要方式。岩石在动载荷作用下的破坏形式尤为受到关注[1-6]。众多学者对含初始缺陷岩石在冲击载荷作用下裂纹扩展规律及最终破坏形式进行了大量的研究，取得了很多较好的研究成果。Wang等[7]采用SCSC试件研究了复合型裂纹在冲击载荷作用下的扩展特性，并对裂纹扩展过程中的扩展速度进行了初步分析。Wang等[8-10]采用试验-数值法进行了CSTFBD试件在冲击载荷作用下裂纹尖端应力强度因子的求解，并对动态起裂韧度与动态扩展韧度进行了计算。Zhang等[11, 12]对冲击载荷作用下岩石中裂纹尖端的测试方法进行了系统的总结与分析，并对在不同动态加载率作用下动态断裂韧度进行计算与分析。宋义敏等[13-15]采用自制的落锤冲击试验机研究了冲击载荷I型裂纹尖端位移场的演化过程，并对冲击加载作用下裂纹扩展速度及裂纹扩展距离随时间的变化规律进行了定量分析。
随着冲击载荷作用下初始缺陷岩石破坏规律得到了大量研究的论证，深部巷道结构在爆炸与冲击等动载荷作用下的破坏规律也越来越受到国内外众多研究学者的关注。潘一山等[16]利用爆炸加载相似模拟试验和数字散斑观测方法（DSCM），研究高速冲击载荷作用下巷道动态破坏行为。郭东明等[17-19]采用爆破加载方式与数字激光动态焦散线试验系统相结合，探究了巷道爆破开挖对邻近巷道预制裂纹群的影响规律。
近年来，随着霍普金森压杆(split Hopkinson press bar, SHPB)试验设备的发展与改进，较多的研究学者采用此试验装置来研究各种脆性材料在冲击载荷作用下的破坏规律，大量的研究结果已经得到发表[20-24]。由于SHPB杆件目前最大直径为100 mm，对于研究在冲击载荷作用下较大巷道模型内裂纹扩展规律及裂纹扩展速度等问题，具有一定的局限性，为了充分地研究巷道内围岩中裂纹对巷道破坏形式的影响，本文采用能实现中低速冲击加载的落锤冲击试验机进行动态断裂试验，随后利用致密隆昌青砂岩进行试件的制作，探讨巷道内裂纹在快速扩展过程中裂纹扩展规律，以期为巷道内爆破施工等问题提供一定的理论依据。
1. 模型设计
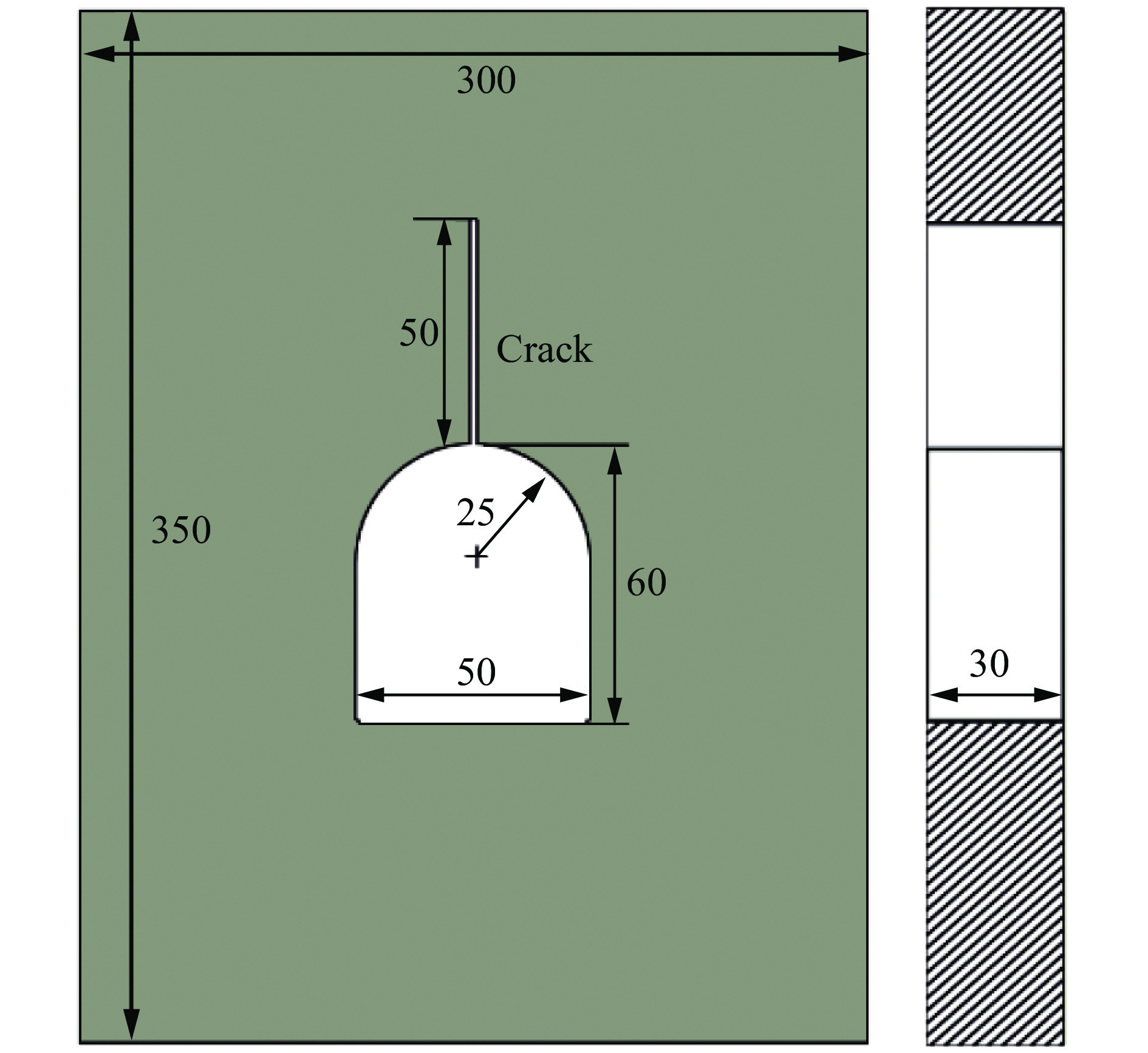
根据研究的实际情况和试验条件，详细地分析预制裂纹对巷道破坏行为的影响，并对裂纹扩展速度变化规律进行定量分析。首先对巷道模型进行相关的数值模拟计算，分析冲击载荷作用下巷道内裂纹的扩展特性及巷道模型的破坏行为。以某深部地下采矿巷道断面高6 m、宽5 m，圆弧拱半径2.5 m为原型，以该实际工程巷道断面形状按比例100∶1进行整体缩小设置。巷道模型断面高60 mm，宽50 mm，圆弧拱半径为25 mm，巷道模型试样尺寸为300 mm×350 mm×30 mm。为了考虑围岩内裂纹缺陷对巷道模型的影响，在巷道的拱顶对称轴线上设置预制单裂纹，裂纹长度2a=50 mm，与巷道断面跨度比值为1∶1，该巷道模型能够很好地表观在静态载荷作用下对巷道模型稳定性的影响[25-28]，如图1所示。
1.1 数值模型
本文采用 AUTODYN有限差分法软件进行数值分析，得到冲击载荷作用下裂纹扩展速度、起裂时间的变化规律及裂纹扩展特性。AUTODYN 是一款高度显式非线性动力求解算法软件，该软件能够较好地分析几何非线性与材料非线性等岩石类冲击与爆炸载荷作用下的断裂行为响应，可以解决高度非线性动力学研究相关问题，内部包含多种材料损伤模型和材料参数数据库，并能和ANSYS模块的其他有限元求解器及 CAE软件较好地整合在一起，进一步提高了动态载荷作用下求解的精准度，较多的研究学者已经广泛地将该软件应用于动态载荷作用下的相关课题，并验证了该软件计算方法的有效性[29-32]。
岩石类等脆性材料采用的本构关系需要满足材料的强度与开裂参数要求，因此本文采用最大剪应力破坏准则与最大主应力破坏准则来描述砂岩材料的破坏形态，即当一个微观材料单元的最大剪应力超过材料允许的最大剪切强度时，这个材料的微观单元就将失效破坏，或当一个微观材料单元的最大主应力超过材料允许的最大拉伸强度时，这个材料的微观单元就将失效破坏，如下式[29]：
τmax (1) 式中：
{\tau _{\max }} 为最大剪切应力值；{\tau _c} 为最大剪切强度；{\sigma _1} 为最大主应力值；{\sigma _{\rm T}} 为最大拉伸强度。在数值分析的过程中，由于试验测试过程中的变形和应力都不是很大，所以将线性状态方程应用到所有材料中，线性状态方程可以表达为下式：
p(\rho ) = K \left(\frac{\rho }{{{\rho _0}}} - 1\right) (2) 式中：p为损伤状态所受压力；K为体积模量；ρ0与ρ分别为材料初始状态密度与损伤状态密度。
由于选择的模型材料为脆性青砂岩，砂岩抗压强度远大于抗拉强度与抗剪强度，且受剪时颗粒会膨胀，强度模型采用针对脆性岩石材料使用较为广泛的Drucker-Prager准则，参数中的单轴抗压强度与单轴抗拉强度根据国际岩石力学学会规范中标准单轴抗压与单轴抗拉试验进行砂岩参数测试，力学性质参数如表1所示。
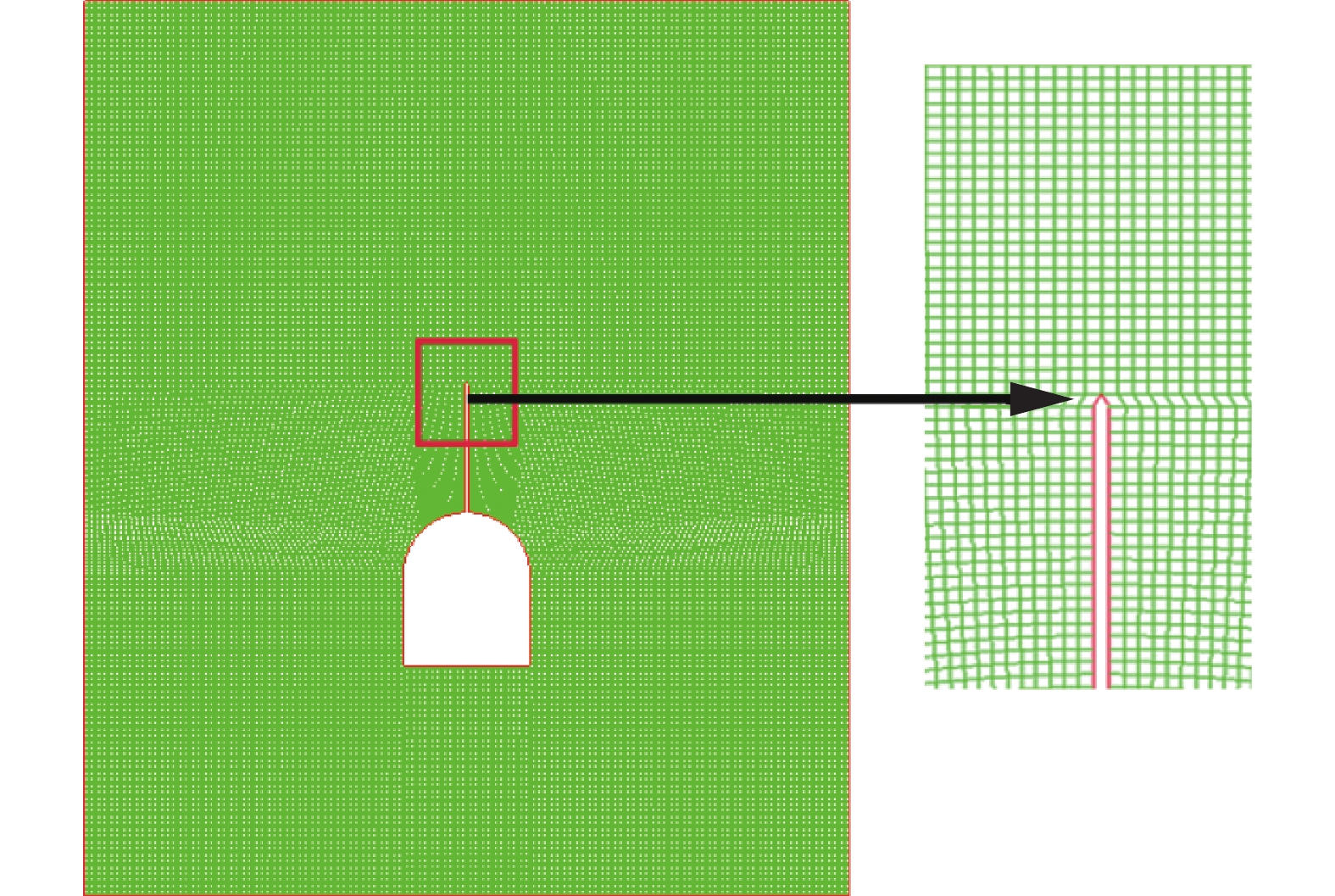
表 1 砂岩及杆件材料参数Table 1. Material parameters of sandstone and LY12CZ材料 ρ/(kg∙m−3) σc/(MPa) σt/(MPa) KIC/(MPa∙m1/2) Ed/(GPa) νd cd/(m·s−1) cs/(m·s−1) cR/(m·s−1) LY12CZ 2850 71.7 0.3 5006 砂岩 2265 22.08 1.08 0.468 13.58 0.164 2563 1639 1479.9 注：ρ为密度，σc为单轴抗压强度，σt为单轴抗拉强度，KIC为静态断裂韧度，Ed为弹性模量，νd为泊松比，cd为纵波波速，cs为横波波速，cR为瑞雷 波波速. 基于图1尺寸模型建立3D有限元数值模型，模型实体的网格单元采用六面体非结构化网格单元，模型共有99 550个单元和507 300个节点，网格单元如图2所示，根据冲击试验装置建立相应的数值模型，采用落锤冲击速度v =2～9 m/s进行数值模拟，以0.5 m/s为梯度增量得到各组数值分析结果，总共15组模拟数据，对每1组冲击速度作用下的模拟结果进行统计分析。
1.2 数值模拟结果
详细分析数值模拟结果中巷道内裂纹在冲击载荷作用下的扩展特性，并将数值分析结果中裂纹扩展路径进行分析，如图3所示。（绿色表示损伤路径，蓝色表示岩石试件）从图中可以看出，预制裂纹为纯I型裂纹扩展特性，扩展路径为相对的直线特性，裂纹起裂方向沿着预制裂纹的原方向竖直向上扩展，且在底板区域由于冲击载荷产生的拉伸应力作用产生拉伸破坏，这与静态载荷作用下巷道模型的破坏方式有较大差别[27-28]。由于砂岩材料具有一定的不均匀性及巷道模型试件加工误差这些因素的叠加影响，试验裂纹扩展路径与数值模拟结果具有一定的偏差，但通过与试验破坏结果进行对比分析可知，两者结果基本一致，表明试验模型设计具有较好的可行性。
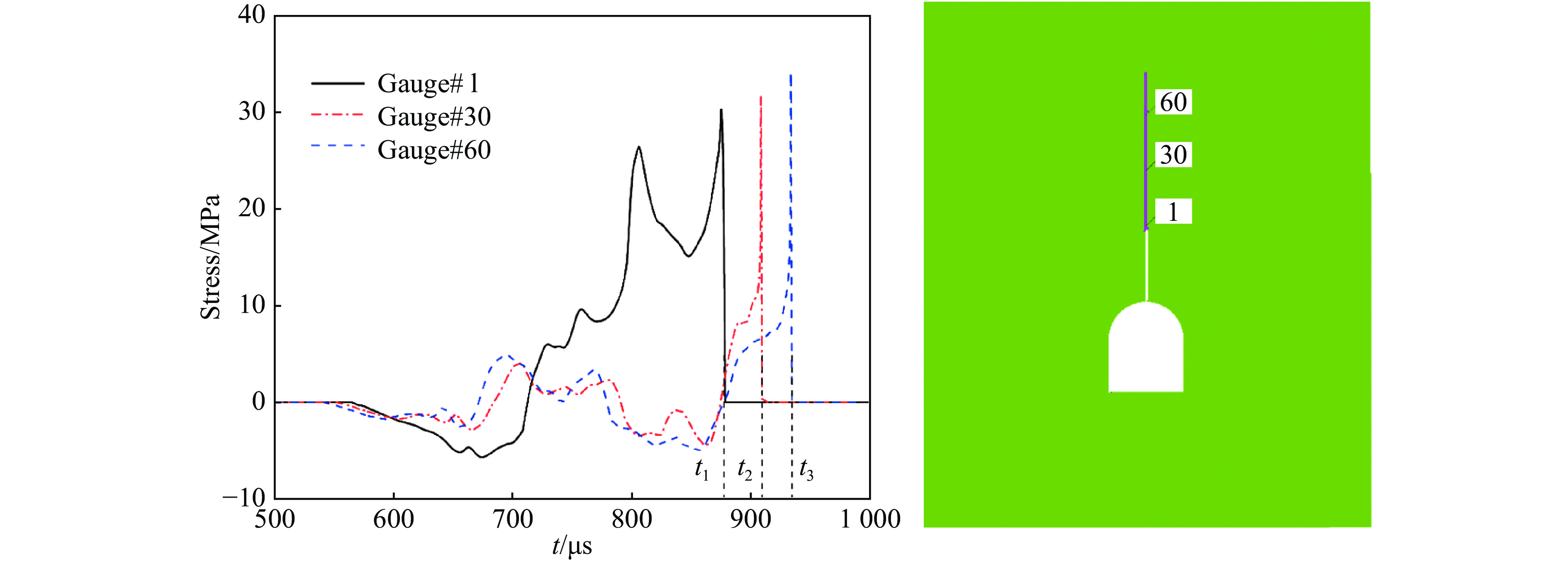
为了充分地分析裂纹的扩展速度变化规律，在裂纹的扩展路径中设置高斯监测点，根据各高斯监测点的最大主应力时程曲线来判断裂纹的扩展速度，如图4所示，随后与试验测得的裂纹扩展速度进行对比分析。当某一网格单元破坏，达到完全失效状态，该高斯点应力峰值将迅速降为零，表示裂纹扩展至某一高斯点处，如t1、t2、t3时分别为高斯点1、30、60位置处的断裂时刻，再根据每处高斯点的断裂时刻即可求解出各位置处裂纹的扩展平均速度。
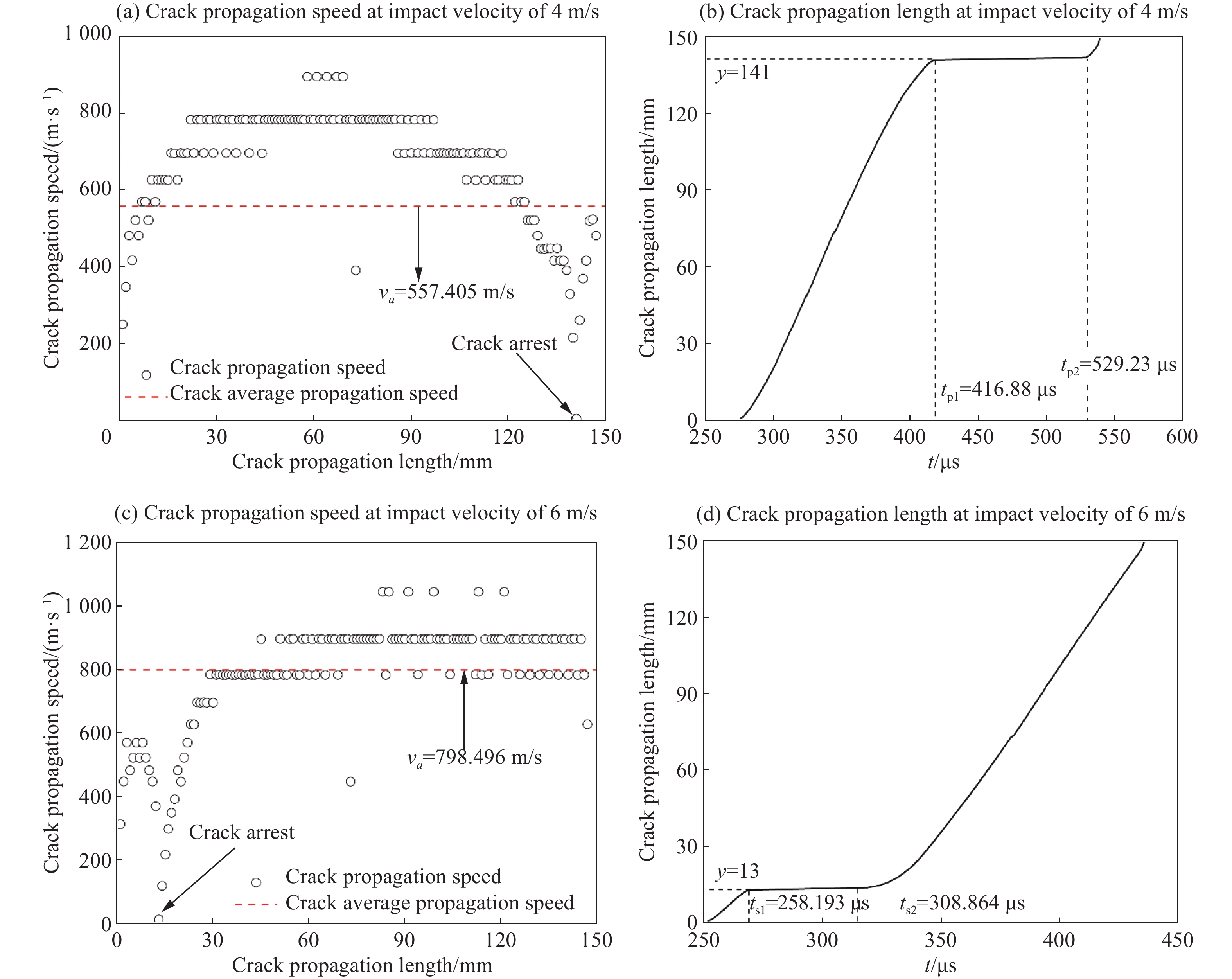
从图5(a)落锤冲击速度v = 4 m/s的数值分析结果可以看出，裂纹的扩展速率在不断的变化，裂纹的最大扩展速度vmax=894.09 m/s，裂纹的最小扩展速度vmin=8.901 m/s，裂纹的平均扩展速度为va=557.405 m/s。当裂纹尖端扩展至141 mm时，裂纹的扩展速度仅为8.901 m/s，裂纹扩展速度远小于其他位置处的裂纹扩展速度，表明在此位置处发生了止裂现象。从图5(b)裂纹尖端扩展位移时程曲线更加明显地说明了这一现象的存在，当裂纹扩展至141 mm位置时，裂纹止裂时间长达t=tp2−tp1=112.35 μs。图5(c)为v= 6 m/s的冲击速度作用下裂纹扩展速度分布情况，此时裂纹的最大扩展速度vmax= 1 043.339 m/s，裂纹的最小扩展速度vmin= 19.735 m/s，裂纹的平均扩展速度va= 798.496 m/s。当裂纹扩展至13 mm时，裂纹扩展速度为19.735 m/s，表明此时裂纹扩展速度较小，同理，止裂现象发生于此位置处。从图5(d)裂纹尖端扩展位移趋势线可以计算出，裂纹尖端扩展至13 mm位置处裂纹大约停滞了t=ts2−ts1=50.671 μs。这说明在不同冲击载荷作用下，裂纹的平均扩展速度va与止裂时间不尽相同。
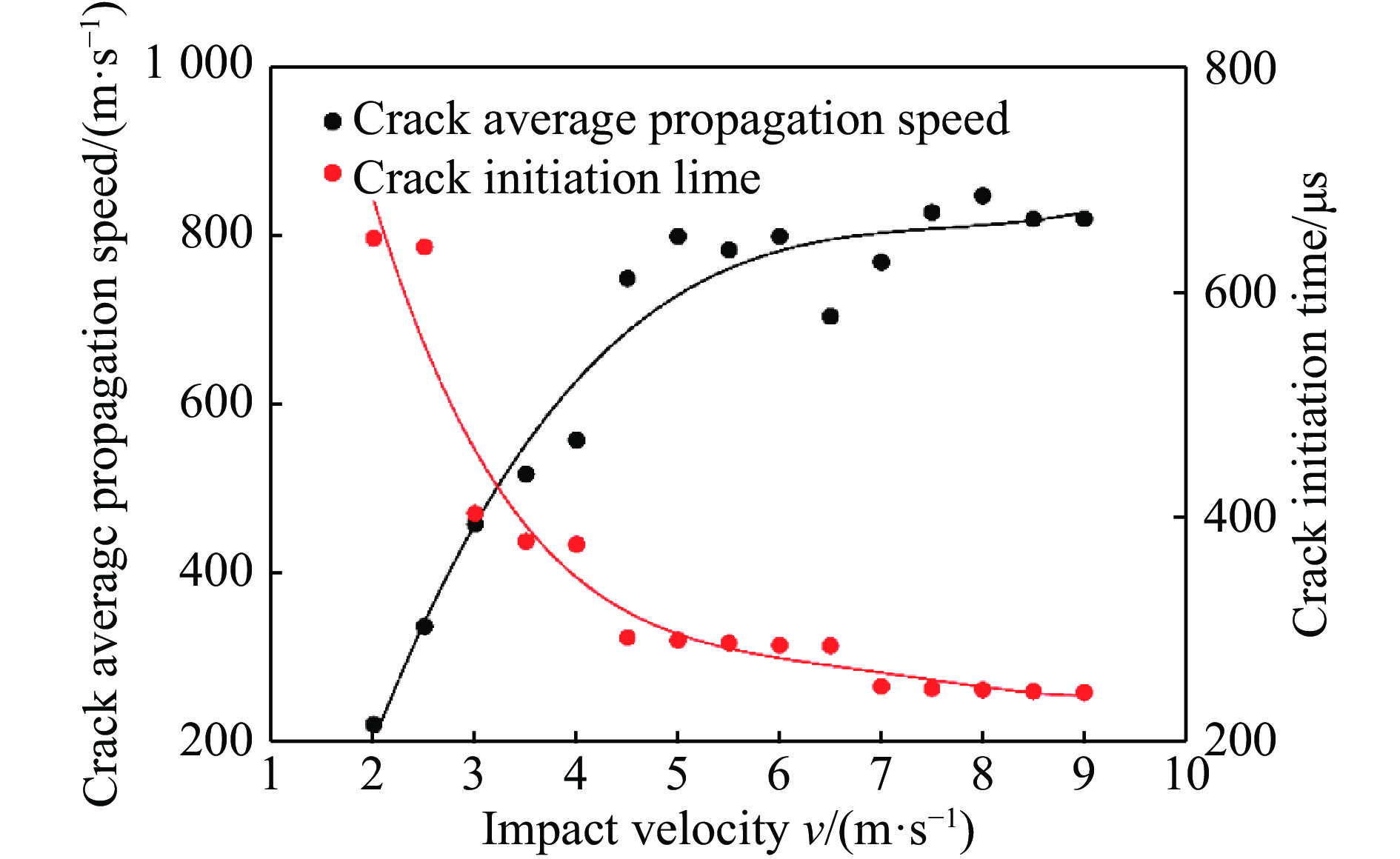
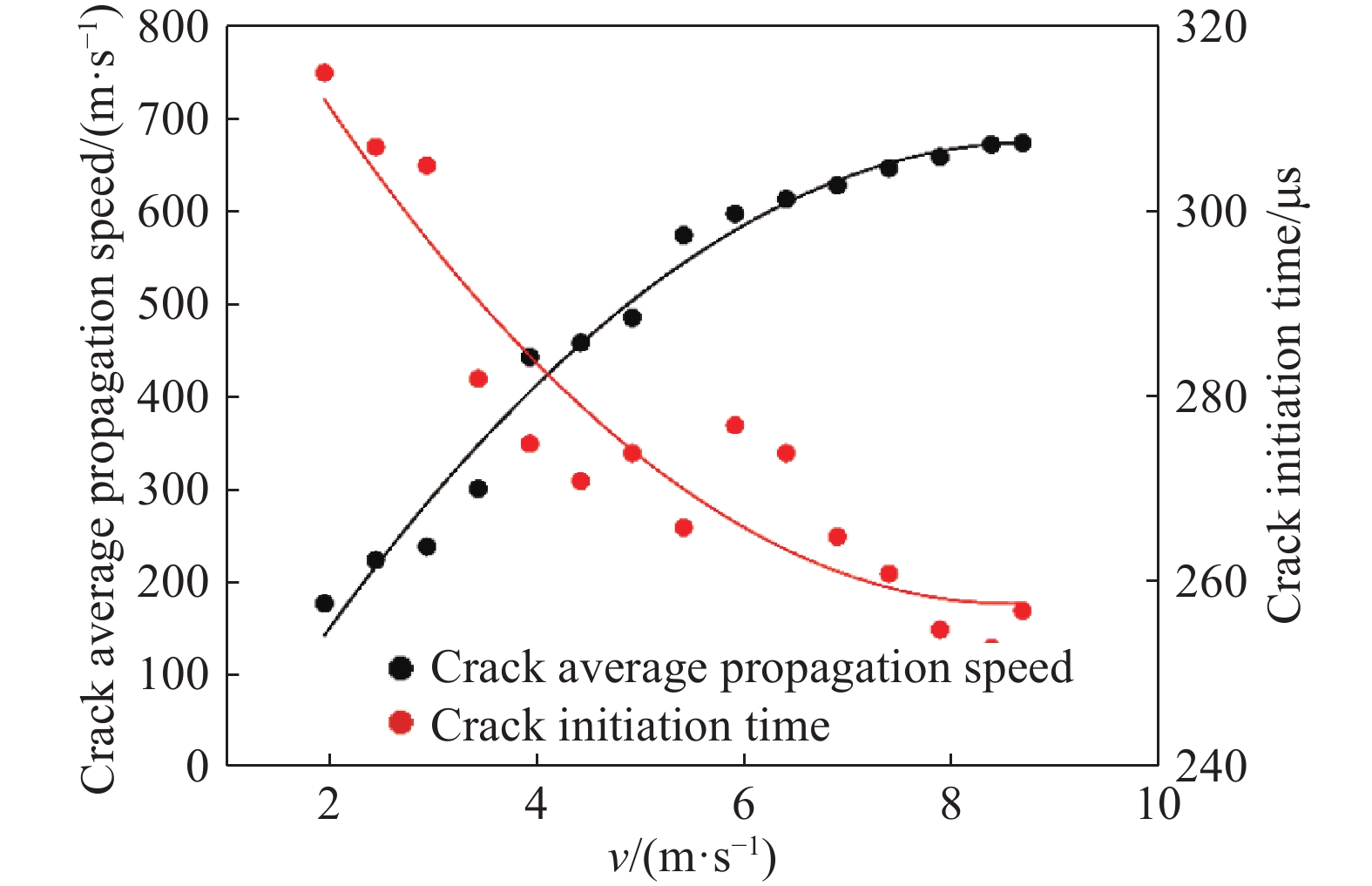
随后将v= 2～9 m/s内落锤不同冲击速度作用下裂纹平均扩展速度与起裂时间进行统计分析，得到不同冲击速度作用下裂纹扩展速度与起裂时间的趋势线，如图6所示。可以看出，随着冲击速度的增加，裂纹平均扩展速度逐渐趋于稳定，最后进行了相应的函数拟合，拟合函数列于图中，吻合系数能够达到0.951 1。从图中也可以看出，随着冲击速度的增加，起裂时间越短，最后也给出了相应的函数拟合，吻合系数为0.943 2。
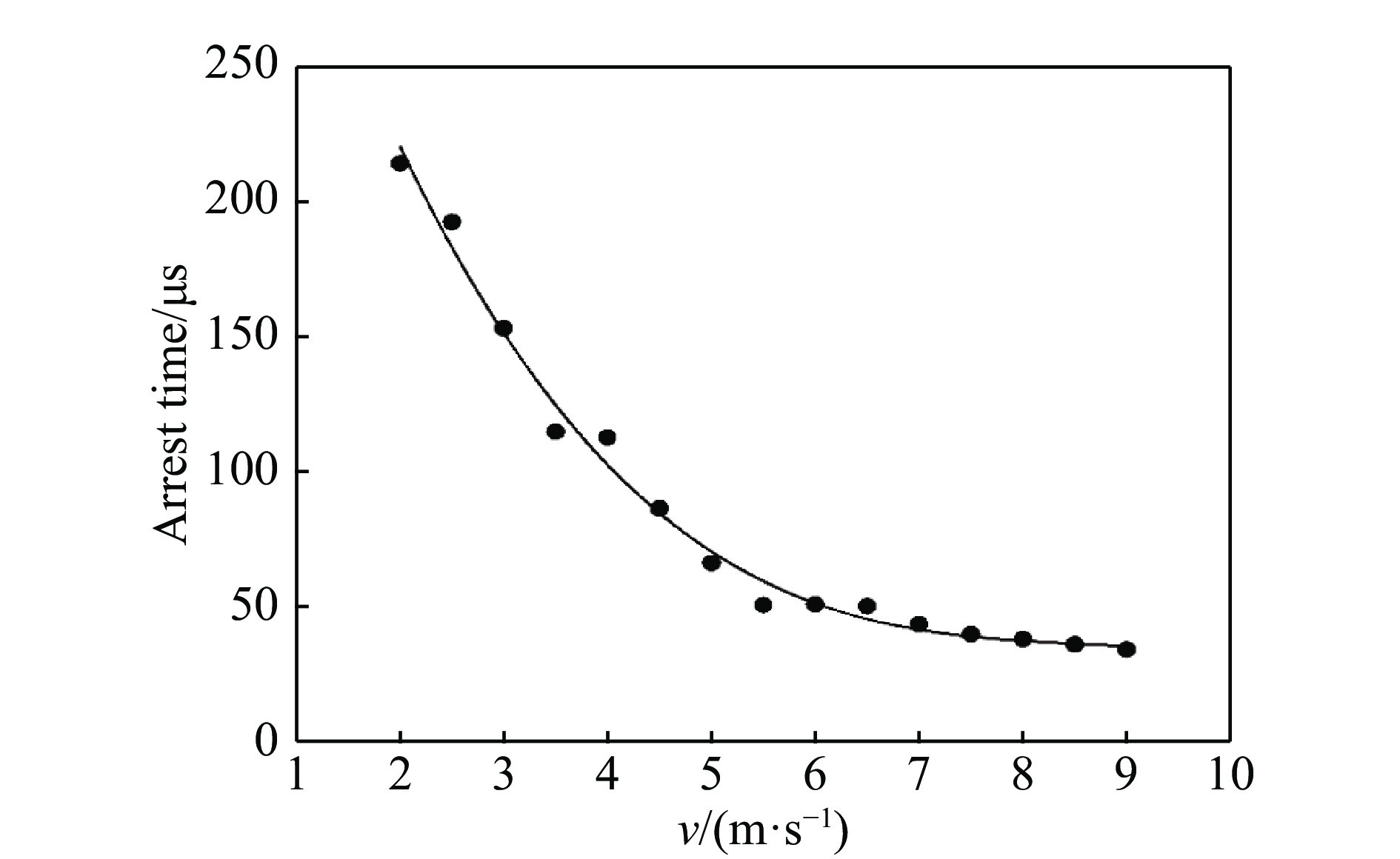
图 6 裂纹平均扩展速度与起裂时间趋势线Figure 6. The trendline of crack average propagation velocity and initiation time在裂纹的扩展路径中，监测到了止裂现象的存在，将每组裂纹扩展过程中的止裂时间进行计算分析，得到如图7的趋势线，从图中可以看出，裂纹的止裂时间随着冲击加载速度的增加，裂纹止裂时间逐渐变短，并最终趋于稳定，随后进行相应的函数拟合，吻合系数达到0.990 1。这是由于冲击速度越大，产生的冲击能量越大，能提供达到巷道模型试件再次起裂的能量就越大，试件止裂时间区间就越短。
2. 试验方案
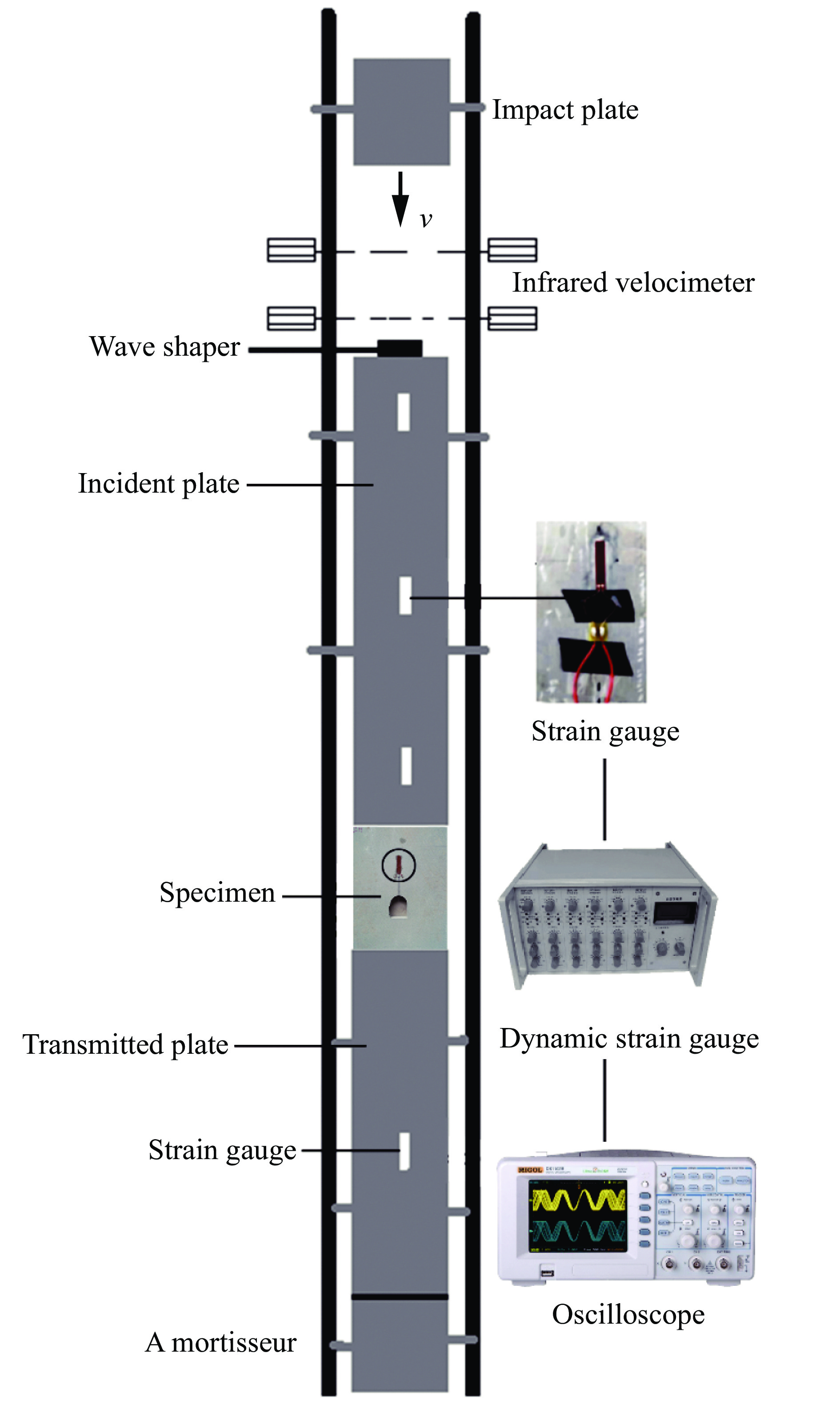
本文采用落锤冲击试验装置进行动态断裂试验，试验装置如图8所示，动态加载装置与数据采集系统均基于SHPB试验设备系统进行安装，将材料LY12CZ铝合金作为入射板与透射板原材料，该材料的弹性模量为71.7GPa，泊松比为0.3，密度为2 850 kg/m3，入射板长度l1=3 000 mm，透射板长度l2=2 000 mm，入射板与透射板的宽度及厚度相同，均为300 mm×30 mm。随后在入射板与透射板上分别粘贴BX120-10AA应变片来测试冲击载荷作用下的应变信号，入射板上的应变片距离试件上端面分别为500，1 500和2 500 mm，最后经过初步测试选择500 mm处应变片作为入射端采集信号端；透射端上的应变片位于透射板中部，距离试件下端面距离为1 000 mm。落锤下落的冲击速度可根据试验测试要求任意设置，下落高度根据数值模拟结果选择h= 0.2～4.5 m，下落冲击速度采用红外线测距仪进行测试，巷道模型的加载方式如图8所示。
为了使加载波形为理想的光滑半正弦波，在入射板与透射板之间粘贴黄铜片充当波形整形器，该措施不仅能够延长波长的加载时间，而且能够减少波形振荡作用产生的弥散效应；除此之外，摩擦因素是所有压缩试验是否有效的一个关键因素，因此在测试的过程中，需要在巷道模型试件与入射板、透射板之间涂抹少量凡士林作为润滑剂，减小试件与入射端、透射端之间摩擦效应的影响。
2.1 试验材料
为了很好地监测裂纹扩展速度，须将巷道模型理想化为连续介质力学及离散元模型，所以选用质密且粒径均匀的隆昌青砂岩作为试验材料。由于砂岩是一种沉积岩，主要是由砂粒胶结堆积而成，内部结构稳定，颗粒细腻，比较均匀，采用砂岩作为模型材料进行模型试验符合裂纹扩展速度观测的要求[25]。该材料的力学性质参数如表1所示。巷道模型试件首先采用高速冲切水刀进行加工成含巷道孔洞的300 mm×350 mm×30 mm的长方体砂岩块，裂纹宽度为1 mm，裂纹的加工使用1 mm厚的薄钢锯条加工至48 mm，再采用0.2 mm的美工刀片进行2 mm裂尖锐化，裂尖宽度小于0.4 mm，该处理措施能够很好地符合国际岩石力学学会对岩石试样裂纹尖端宽度制作要求，巷道模型试件如图3所示，总共制作20组试验模型试件。
2.2 冲击试验
当落锤以一定的速度冲击入射板后，在入射板中即产生一入射波脉冲信号向前传播，由超动态应变仪记录应变片信号并进行信号放大，随后采用高速示波器转换成电压信号进行采集，电压信号经过转换成应变信号即得到入射波应变信号εi(t)。弹性压缩波继续向下传播至杆件与试样的交界面处，由于两者之间波阻抗不一样，因而波在入射端与试件边界面发生反射与透射，应力波一部分经过反射重新传入入射板中，得到反射波应变信号εr(t)；应力波一部分经过透射传入试件中，使巷道模型试件压缩变形引起预制裂纹起裂破坏。当应力波穿过试件传入透射板与试件的交界面时，波在边界面继续产生透射与反射，当波透射进入透射板中，可以通过透射端应变片采集得到透射波应变信号εt(t)。随后将应变信号进行力的转换得到巷道模型试件上端面的动态载荷pi(t)与下端面的动态载荷pt(t)，转换关系如下式
\left. \begin{gathered} {p_{\rm i}}(t) = EA[{\varepsilon _{\rm i}}(t) + {\varepsilon _{\rm{r}}}(t)] \\ {p_{\rm t}}(t) = EA{\varepsilon _{\rm t}}(t) \\ \end{gathered} \right\} (3) 式中：E为弹性杆件的弹性模量，A为弹性杆件的横截面积。
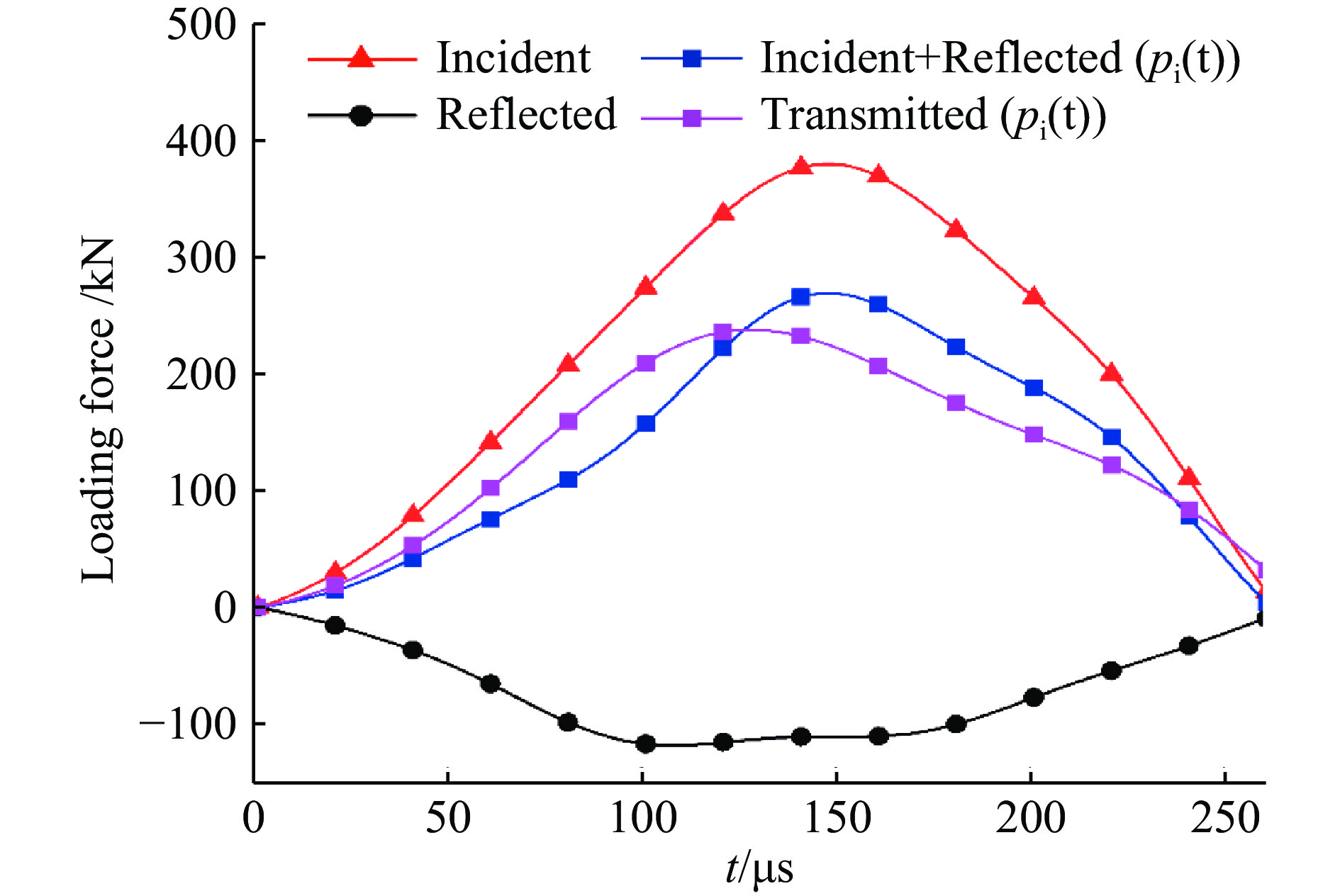
按照唐志平等[33]和刘德顺等[34]提出的SHPB试验装置动态载荷处理方法，同时找到入射波、反射波及透射波的波头，通过式(3)的叠加计算冲击加载试样上下两端的动载荷，如图9所示。依据SHPB 装置的均匀化条件假设，应力波经过多次反射后，上下两个端面的应力、应变应该趋于平衡。从图9可以看出，经过几次透反射后，巷道模型试件两端的应力、应变基本达到一致，符合动态试验要求。
3. 裂纹扩展计的应用
为了实际监测裂纹扩展过程中的裂纹扩展速度变化，本文采用裂纹扩展计(crack propagation gauge, CPG)测定巷道内裂纹在较长试件范围内的动态起裂时间与扩展速度。CPG在测试裂纹起裂和扩展上具有简单、灵敏等优点[35]。在巷道模型试样正面的裂纹尖端沿裂纹扩展方向粘贴CPG，其构造如图10所示。该CPG由21根宽度不同，长度都为h=10 mm，且由并联布置的金属栅丝组成。相邻2个金属栅丝丝之间的间距相同，都为l0= 2.2 mm，总距离l=44 mm。为了准确测试预制裂纹的起裂时间，粘贴CPG时，将CPG第1根电阻丝与预制裂纹尖端重合，这样能够很好地确定预制裂纹的起裂时间ti。
3.1 CPG测试数据
当巷道内预制裂纹开始起裂时，CPG 的第 1 根金属栅丝开始断裂，促使并联电阻阻值增大，最终形成 CPG两端的电压信号逐渐增大。随着预制裂纹的逐渐向前扩展，断裂的金属栅丝数量逐渐增多，而电压信号也呈现台阶变化，直至第21根金属栅丝断裂，电压信号呈现直线信号，如图11所示。
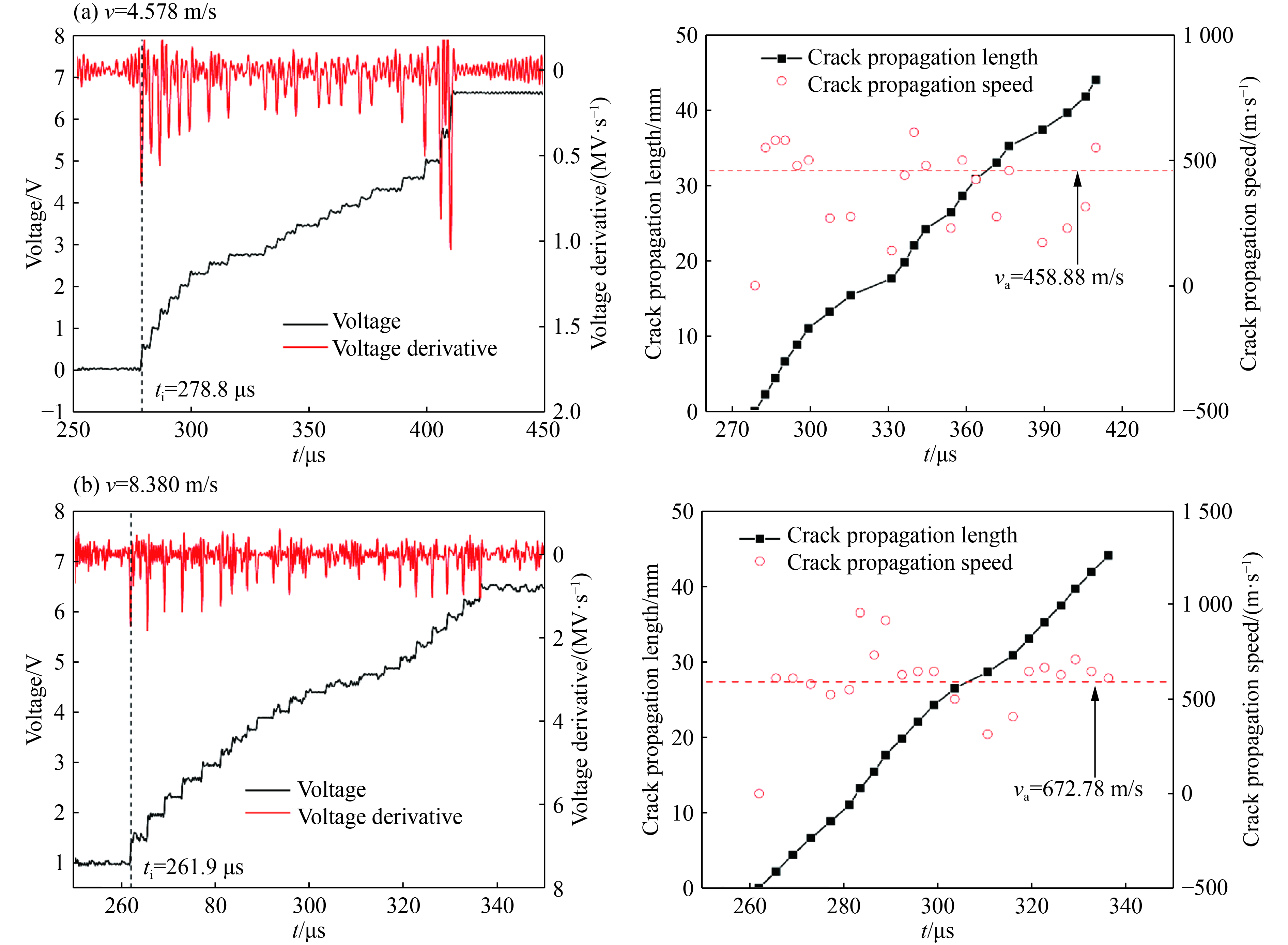
通过对每一台阶信号变化的裂纹扩展速度进行统计分析可知，裂纹在整个扩展过程中，裂纹扩展速度不是一个定值，在逐渐上下波动。从图11(a)可以看出，在冲击速度v=4.578 m/s载荷作用下，裂纹扩展过程中的最大速度vmax= 611.11 m/s，最小扩展速度为vmin=139.24 m/s，裂纹的平均扩展速度为va= 458.88 m/s；在冲击速度v=8.380 m/s载荷作用下，裂纹扩展过程中的最大速度vmax= 956.52 m/s，最小扩展速度为vmin=314.28 m/s，裂纹的平均扩展速度为va= 672.78 m/s。在不同冲击载荷作用下巷道内预制裂纹的起裂时间也不相同，当冲击速度v=4.578 m/s时，裂纹的起裂时间为278.8 μs；当冲击速度v=8.308 m/s时，裂纹的起裂时间为261.9 μs。
由于冲击试验偶然性的原因，仅测试出15组冲击速度载荷作用下的试验数据，随后将每组的起裂时间与裂纹平均扩展速度va进行总结，如表2所示。
表 2 CPG测试结果Table 2. CPG test results试件编号 v/(m∙s−1) ti/μs va/(m∙s−1) 试件编号 v/(m∙s−1) ti/μs va/(m∙s−1) 1 1.939 315 177.957 9 5.903 277 598.180 2 2.435 307 224.744 10 6.398 274 613.668 3 2.930 305 239.419 11 6.893 265 628.571 4 3.425 282 301.829 12 7.389 261 647.059 5 3.921 275 443.548 13 7.884 255 659.176 6 4.578 279 458.881 14 8.380 262 672.780 7 4.912 274 486.189 15 8.683 257 674.386 8 5.407 266 574.912 3.2 试验结果分析
为了验证数值分析结果的准确性，随后将每组裂纹的起裂时间与裂纹平均扩展速度进行总结，得到如图12所示的趋势线，从图中可以看出，裂纹平均扩展速度随着冲击速度的增加而增加，最终趋于稳定，随后进行函数拟合，吻合系数为0.980 4；裂纹起裂时间随着冲击速度的增加而逐渐减小，最后也逐渐趋于稳定，并在稳定值上下波动，随后也进行相应的函数拟合，吻合系数为0.885 6。预制裂纹的起裂时间随着冲击速度的增加而减小，这是由于低速冲击载荷作用下，岩石脆性材料变形中只包含了一部分微观裂纹。随着动态加载率的增加，越来越多的微裂纹参与到变形当中，直至达到某一动态加载率的峰值，所有微裂纹均参与动态断裂，且在达到这一峰值后，起裂时间在某一值上下起伏波动。当形成的微观裂纹越多，促使裂纹起裂的时间越短。数值分析结果与试验结果基本吻合，但裂纹平均扩展速度大小有一定的差异，造成这种差异的主要原因是砂岩材料粘结颗粒的不均匀性及试验过程中的能量耗散所造成的。
图 12 试验测试裂纹平均扩展速度与起裂时间结果值Figure 12. Test results of crack average propagation speed and initiation time4. 结 论
通过采用裂纹扩展计进行裂纹扩展速度与起裂时间的测试，与数值分析结果进行对比分析，两者具有较好的一致性，并对巷道围岩内初始裂纹的扩展速度、起裂时间等动态断裂参数进行分析，对止裂现象进行了初步的讨论，获得了以下主要结论：
（1）在砂岩巷道围岩中的初始裂纹缺陷，裂纹扩展速度不是恒定值，在不断的围绕裂纹扩展速度平均值上下波动。随着冲击载荷的增大，裂纹平均扩展速度逐渐增加，最终趋于稳定值。
（2）随着冲击速度载荷的增加，裂纹起裂时间逐渐变小，最终趋于在稳定值上下波动。
（3）裂纹扩展路径中存在止裂现象，止裂时间的长短与冲击载荷的大小有很大关系，随着冲击速度的增加，裂纹止裂时间越短，并逐渐趋于稳定。
（4）AUTODYN作为一款有限差分法显示动力学求解软件，能够很好地分析冲击载荷作用下巷道内裂纹的扩展特性，也能够较好地分析巷道内微观裂纹群的形成机制。
-
图 6 裂纹平均扩展速度与起裂时间趋势线
Figure 6. The trendline of crack average propagation velocity and initiation time
图 12 试验测试裂纹平均扩展速度与起裂时间结果值
Figure 12. Test results of crack average propagation speed and initiation time
表 1 砂岩及杆件材料参数
Table 1. Material parameters of sandstone and LY12CZ
材料 ρ/(kg∙m−3) σc/(MPa) σt/(MPa) KIC/(MPa∙m1/2) Ed/(GPa) νd cd/(m·s−1) cs/(m·s−1) cR/(m·s−1) LY12CZ 2850 71.7 0.3 5006 砂岩 2265 22.08 1.08 0.468 13.58 0.164 2563 1639 1479.9 注：ρ为密度，σc为单轴抗压强度，σt为单轴抗拉强度，KIC为静态断裂韧度，Ed为弹性模量，νd为泊松比，cd为纵波波速，cs为横波波速，cR为瑞雷 波波速. 
下载: 导出CSV
表 2 CPG测试结果
Table 2. CPG test results
试件编号 v/(m∙s−1) ti/μs va/(m∙s−1) 试件编号 v/(m∙s−1) ti/μs va/(m∙s−1) 1 1.939 315 177.957 9 5.903 277 598.180 2 2.435 307 224.744 10 6.398 274 613.668 3 2.930 305 239.419 11 6.893 265 628.571 4 3.425 282 301.829 12 7.389 261 647.059 5 3.921 275 443.548 13 7.884 255 659.176 6 4.578 279 458.881 14 8.380 262 672.780 7 4.912 274 486.189 15 8.683 257 674.386 8 5.407 266 574.912
下载: 导出CSV
-
[1] 李地元, 成腾蛟, 周韬, 等. 冲击载荷作用下含孔洞大理岩动态力学破坏特性试验研究 [J]. 岩石力学与工程学报, 2015, 34(2): 249–260.LI Diyuan, CHENG Tengjiao, ZHOU Tao, et al. Experimental study of the dynamic strength and fracturing characteristics of marble specimens with a single hole under impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 249–260. [2] 杨井瑞, 张财贵, 周妍, 等. 用CSTBD试样确定砂岩的动态起裂和扩展韧度 [J]. 爆炸与冲击, 2014, 34(3): 264–271. DOI: 10.11883/1001-1455(2014)03-0264-08.YANG Jingrui, ZHANG Caigui, ZHOU Yan, et al. Determination of dynamic initiation toughness and propagation toughness of sandstone using CSTBD specimens [J]. Explosion and Shock Waves, 2014, 34(3): 264–271. DOI: 10.11883/1001-1455(2014)03-0264-08. [3] 潘峰, 党发宁, 焦凯, 等. 冲击荷载作用下不均匀脆性材料动态弯拉强度提高机制研究 [J]. 岩石力学与工程学报, 2015, 34(S2): 3948–3955.PAN Feng, DANG Faning, JIAO Kai., et al Mechanism on enhancement of dynamic flexural tensile strength for nonuniform brittle materials under impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S2): 3948–3955. [4] 李地元, 邱加冬, 李夕兵. 冲击载荷作用下层状砂岩动态拉压力学特性研究 [J]. 岩石力学与工程学报, 2015(10): 2091–2097.LI Diyuan, QIU Jiadong, LI Xibing. Experimental study on dynamic tensile and compressive properties of bedding sandstone under impact loading [J]. Chinese Journal of Rock Mechanics and Engineering, 2015(10): 2091–2097. [5] LI J C, LI N N, LI H B, et al. An SHPB test study on wave propagation across rock masses with different contact area ratios of joint [J]. International Journal of Impact Engineering, 2017, 105: 109–116. DOI: 10.1016/j.ijimpeng.2016.12.011. [6] 胡柳青, 李夕兵, 龚声武. 冲击载荷作用下裂纹动态响应的数值模拟 [J]. 爆炸与冲击, 2006, 26(3): 214–221.HU Liuqing, LI Xibing, GONG Shengwu. Simulation on dynamic response of crack subjected to impact loading [J]. Explosion and Shock Waves, 2006, 26(3): 214–221. [7] WANG M, ZHU Z, DONG Y, et al. Study of mixed-mode I/Ⅱ fractures using single cleavage semicircle compression specimens under impacting loads [J]. Engineering Fracture Mechanics, 2017, 177: 33–44. DOI: 10.1016/j.engfracmech.2017.03.042. [8] WANG Q, FENG F, NI M, et al. Measurement of mode I and mode Ⅱ rock dynamic fracture toughness with cracked straight through flattened Brazilian disc impacted by split Hopkinson pressure bar [J]. Engineering Fracture Mechanics, 2011, 78(12): 2455–2469. DOI: 10.1016/j.engfracmech.2011.06.004. [9] WANG Q, XING L. Determination of fracture toughness K IC by using the flattened Brazilian disk specimen for rocks [J]. Engineering Fracture Mechanics, 1999, 64(2): 193–201. DOI: 10.1016/S0013-7944(99)00065-X. [10] WANG Q, YANG J, ZHANG C, et al. Sequential determination of dynamic initiation and propagation toughness of rock using an experimental-numerical-analytical method [J]. Engineering Fracture Mechanics, 2015, 141: 78–94. DOI: 10.1016/j.engfracmech.2015.04.025. [11] ZHANG Q B, ZHAO J. Effect of loading rate on fracture toughness and failure micromechanisms in marble [J]. Engineering Fracture Mechanics, 2013, 102(2): 288–309. [12] ZHANG Q B, ZHAO J. Determination of mechanical properties and full-field strain measurements of rock material under dynamic loads [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 60(8): 423–439. [13] 宋义敏, 何爱军, 王泽军, 等. 冲击载荷作用下岩石动态断裂试验研究 [J]. 岩土力学, 2015, 36(4): 965–970.SONG Yiming, HE Aijun, WANG Zhejun, et al. Experiment study of the dynamic fractures of rock under impact loading [J]. Rock and Soil Mechanics, 2015, 36(4): 965–970. [14] 宋义敏, 杨小彬, 金璐, 等. 冲击载荷作用下岩石I型裂纹动态断裂试验研究 [J]. 振动与冲击, 2014, 33(11): 49–53.SONG Yiming, YANG Xiaobin, JIN Lu, et al. Dynamic fracture test for rock I-type crack under impact load [J]. Journal of Vibration and Shock, 2014, 33(11): 49–53. [15] 宋义敏, 杨小彬, 杨晟萱, 等. 冲击载荷下岩石裂纹动态断裂参数研究 [J]. 采矿与安全工程学报, 2015, 32(5): 834–839.SONG Yimin, YANG Xiaobin, YANG Shenxuan, et al. The research of rock dynamic fracture parameter under the action of impact load [J]. Journal of Mining and Safety Engineering, 2015, 32(5): 834–839. [16] 潘一山, 吕祥锋, 李忠华, 等. 高速冲击载荷作用下巷道动态破坏过程试验研究 [J]. 岩土力学, 2011, 32(5): 1281–1286. DOI: 10.3969/j.issn.1000-7598.2011.05.001.PAN Yishan, LÜ Xiangfeng, LI Zhonghua, et al. Experimental study of dynamic failure process of roadway under high velocity impact loading [J]. Rock and Soil Mechanics, 2011, 32(5): 1281–1286. DOI: 10.3969/j.issn.1000-7598.2011.05.001. [17] 郭东明, 刘康, 胡久羡, 等. 爆生气体对邻近硐室背爆侧预制裂纹影响机理 [J]. 煤炭学报, 2016, 41(1): 265–270.GUO Dongming, LIU Kang, HU Jiuxian, et al. Experimental study on the effect mechanism of the explosion gas on the precrack in the back-blasting of adjacent tunnel [J]. Journal of China Coal Society, 2016, 41(1): 265–270. [18] 郭东明, 刘康, 杨仁树, 等. 爆破对邻近巷道背爆侧倾斜裂纹影响实验研究 [J]. 采矿与安全工程学报, 2015, 32(1): 99–104.GUO Dongming, LIU Kang, YANG Renshu, et al. Experimental research on the influence of blasting on the inclined crack in the back-blasting side of nearby roadway [J]. Journal of Mining and Safety Engineering, 2015, 32(1): 99–104. [19] 郭东明, 刘康, 杨仁树, 等. 动静荷载对邻近巷道裂纹缺陷扰动的模拟实验 [J]. 爆炸与冲击, 2016, 36(3): 297–304. DOI: 10.11883/1001-1455(2016)03-0297-08.GUO Dongming, LIU Kang, YANG Renshu, et al. Simulated experiment of disturbance effect on crack defects of adjacent tunnel under dynamic and static load [J]. Explosion and Shock Waves, 2016, 36(3): 297–304. DOI: 10.11883/1001-1455(2016)03-0297-08. [20] 李地元, 韩震宇, 孙小磊, 等. 含预制裂隙大理岩SHPB动态力学破坏特性试验研究 [J]. 岩石力学与工程学报, 2017, 36(12): 2872–2883.LI Diyuan, HAN Zhenyu, SUN Xiaolei, et al. Dynamic mechanical failure characteristics of marble withartificial flawsunder shpb tests [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(12): 2872–2883. [21] 王登科, 刘淑敏, 魏建平, 等. 冲击载荷作用下煤的破坏特性试验研究 [J]. 采矿与安全工程学报, 2017, 34(3): 594–600.WANG Dengke, LIU Shumin, WEI Jianping, et al. The failure characteristics of coal under impact load in laboratory [J]. Journal of Mining and Safety Engineering, 2017, 34(3): 594–600. [22] 袁璞, 马瑞秋. 不同含水状态下煤矿砂岩SHPB试验与分析 [J]. 岩石力学与工程学报, 2015, 34(S1): 2888–2893.YUAN Pu, MA Ruiqiu. Split Hopkinson pressure bar tests and analysis of coalmine sandstone with various moisture contents [J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(S1): 2888–2893. [23] 赵毅鑫, 肖汉, 黄亚琼. 霍普金森杆冲击加载煤样巴西圆盘劈裂试验研究 [J]. 煤炭学报, 2014, 39(2): 286–291.ZHAO Yixin, XIAO Han, HUANG Yaqiong. Dynamic split tensile test of Brazilian disc of coal with split Hopkinson pressure bar loading [J]. Journal of China Coal Society, 2014, 39(2): 286–291. [24] SAKSALA T, HOKKA M, KUOKKALA V T, et al. Numerical modeling and experimentation of dynamic Brazilian disc test on Kuru granite [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59(8): 128–138. [25] 周磊, 朱哲明, 董玉清, 等. 中低速冲击载荷下巷道内裂纹的动态响应 [J]. 岩石力学与工程学报, 2017, 36(6): 1363–1372.ZHOU Lei, ZHU Zheming, DONG Yuqing, et al. Dynamic response of cracks in tunnels under impact loading of medium-low speed [J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(6): 1363–1372. [26] 周磊, 朱哲明, 刘邦. 隧道周边不同位置径向裂纹对隧道围岩稳定性影响规律的研究 [J]. 岩土工程学报, 2016, 38(7): 1230–1237. DOI: 10.11779/CJGE201607009.ZHOU Lei, ZHU Zheming, LIU Bang. Influence of radial cracks on stability of surrounding rocks at different locations around tunnel [J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1230–1237. DOI: 10.11779/CJGE201607009. [27] 周磊, 朱哲明, 刘邦. 裂纹对直墙拱形隧道围岩损伤破坏模式的影响规律研究 [J]. 岩土力学, 2017, 38(12): 3688–3697.ZHOU Lei, ZHU Zheming, LIU Bang. Influence of cracks on surrounding rock damage-failure mode of straight wall arch tunnel [J]. Rock and Soil Mechanics, 2017, 38(12): 3688–3697. [28] ZHOU L, ZHU Z, WANG M, et al. Dynamic propagation behavior of cracks emanating from tunnel edges under impact loads [J]. Soil Dynamic and Earthquake Engineering, 2018, 105: 119–126. DOI: 10.1016/j.soildyn.2017.12.012. [29] ZHU Z. Numerical prediction of crater blasting and bench blasting [J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(6): 1088–1096. DOI: 10.1016/j.ijrmms.2009.05.009. [30] ZHU Z, MOHANTY B, XIE H. Numerical investigation of blasting-induced crack initiation and propagation in rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(3): 412–424. DOI: 10.1016/j.ijrmms.2006.09.002. [31] ZHU Z, XIE H, MOHANTY B. Numerical investigation of blasting-induced damage in cylindrical rocks [J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2): 111–121. DOI: 10.1016/j.ijrmms.2007.04.012. [32] LI M, ZHU Z, LIU R, et al. Study of the effect of empty holes on propagating cracks under blasting loads [J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 103: 186–194. DOI: 10.1016/j.ijrmms.2018.01.043. [33] 唐志平, 王礼立. SHPB实验的电脑化数据处理系统 [J]. 爆炸与冲击, 1986, 6(4): 34–41.TANG Zhiping, WANG Lili. A computerized system of data processing used in SHPB experiments [J]. Explosion and Shock Waves, 1986, 6(4): 34–41. [34] 刘德顺, 李夕兵. 冲击机械系统动力学. 北京: 科学出版社, 1999. [35] ZHANG Q B, ZHAO J. A review of dynamic experimental techniques and mechanical behavior of rock materials [J]. Rock Mechanics and Rock Engineering, 2014, 47(4): 1411–1478. DOI: 10.1007/s00603-013-0463-y. 期刊类型引用(1)
1. 崔新男，汪旭光，王尹军，陈志远. 爆炸加载下混凝土表面的裂纹扩展. 爆炸与冲击. 2020(05): 25-35 . 
本站查看其他类型引用(1)
-
下载:
计量
- 文章访问数: 5249
- HTML全文浏览量: 1514
- PDF下载量: 48
- 被引次数: 2