刚性球体三维高速垂直自由入水载荷

孙玉松; 周穗华; 张晓兵; 孙玉明

doi:10.11883/bzycj-2018-0094

刚性球体三维高速垂直自由入水载荷

doi: 10.11883/bzycj-2018-0094

1.
海军工程大学兵器工程学院，湖北武汉 430033
2.
91267部队，福建福州 350000

详细信息

作者简介:
孙玉松（1991－　），男，博士研究生，751513324@qq.com

中图分类号: O353.4
计量
- 文章访问数: 6313
- HTML全文浏览量: 1999
- PDF下载量: 57
- 被引次数: 0
出版历程
- 收稿日期: 2018-03-22
- 修回日期: 2018-08-10
- 网络出版日期: 2019-04-25
- 刊出日期: 2019-06-01

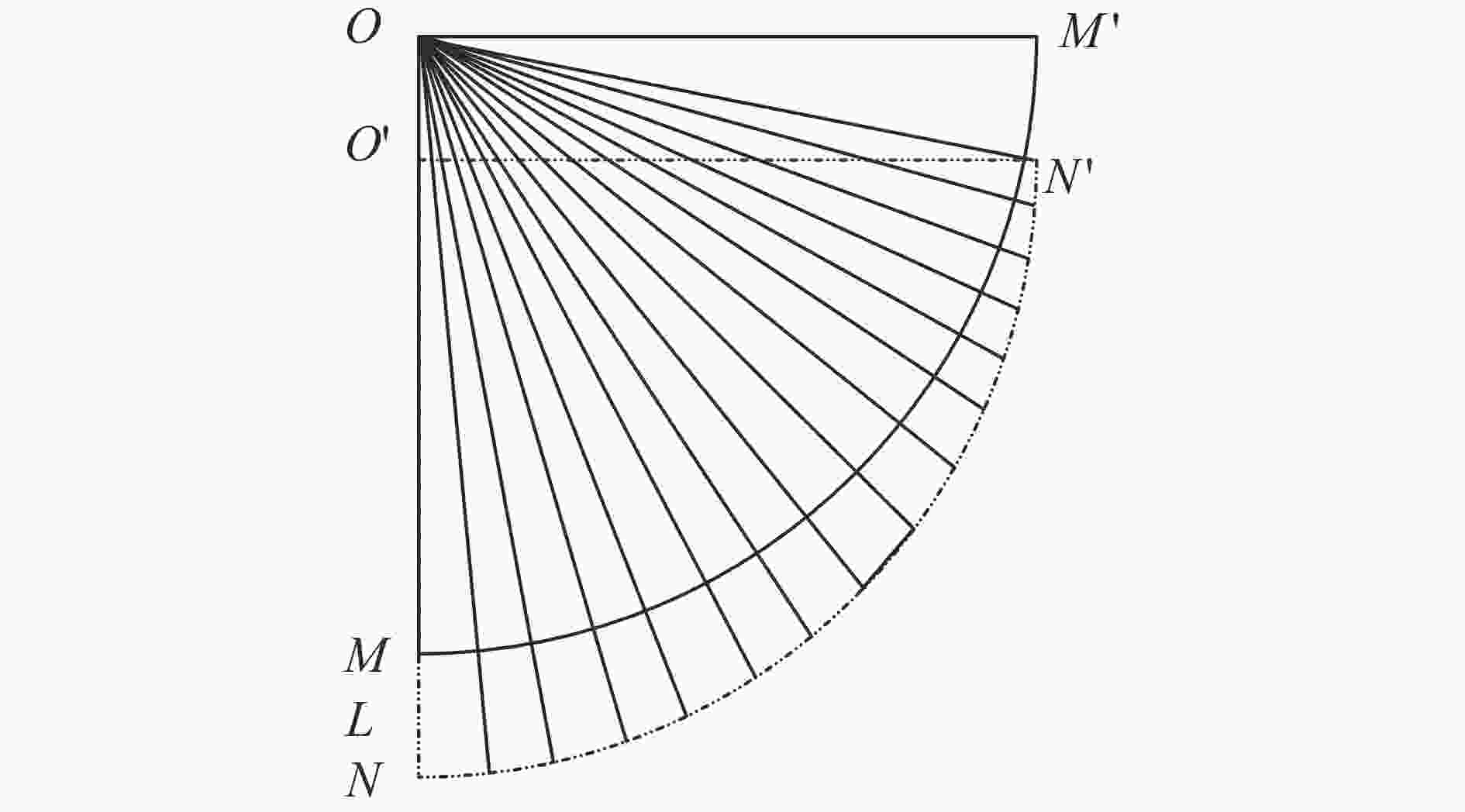
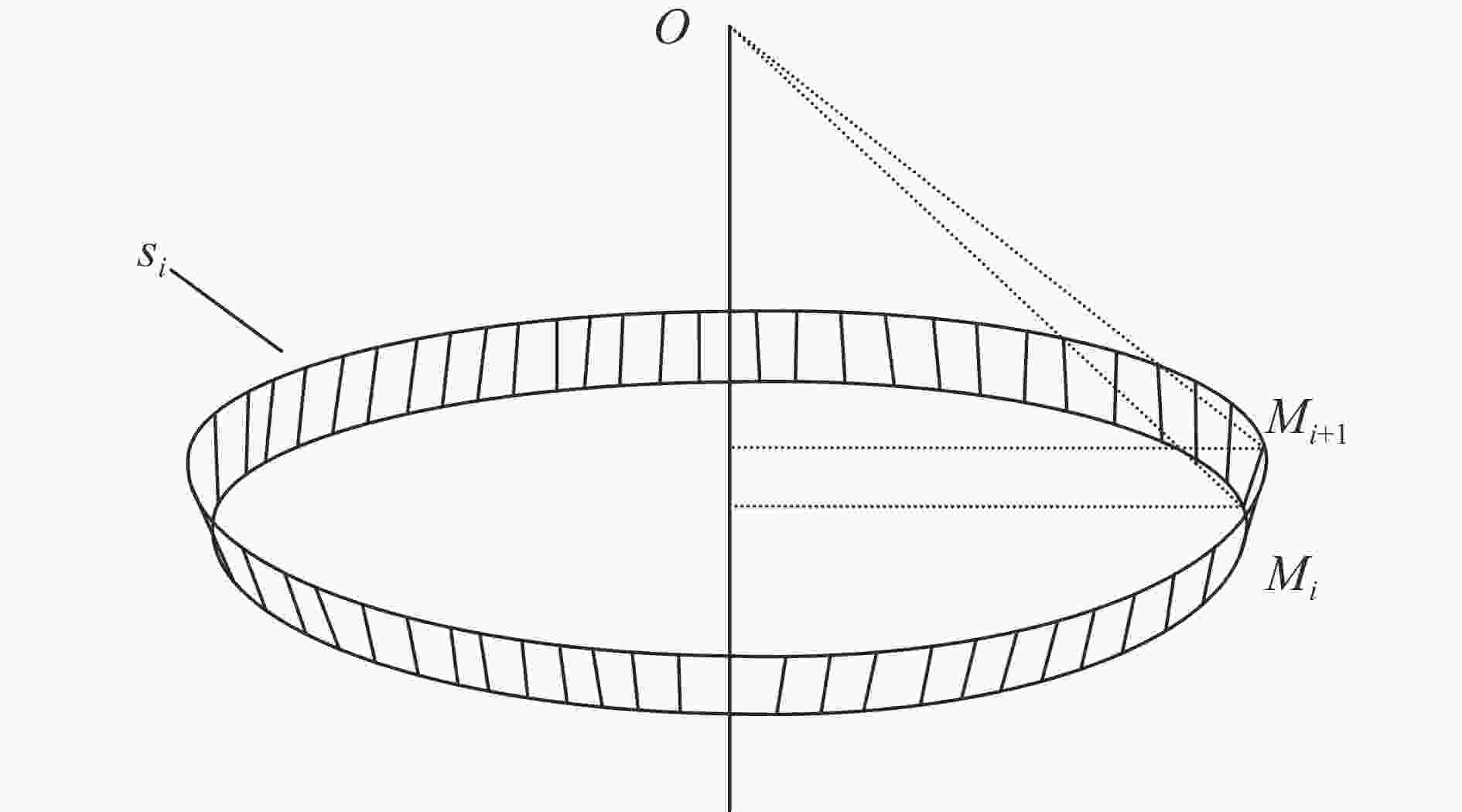
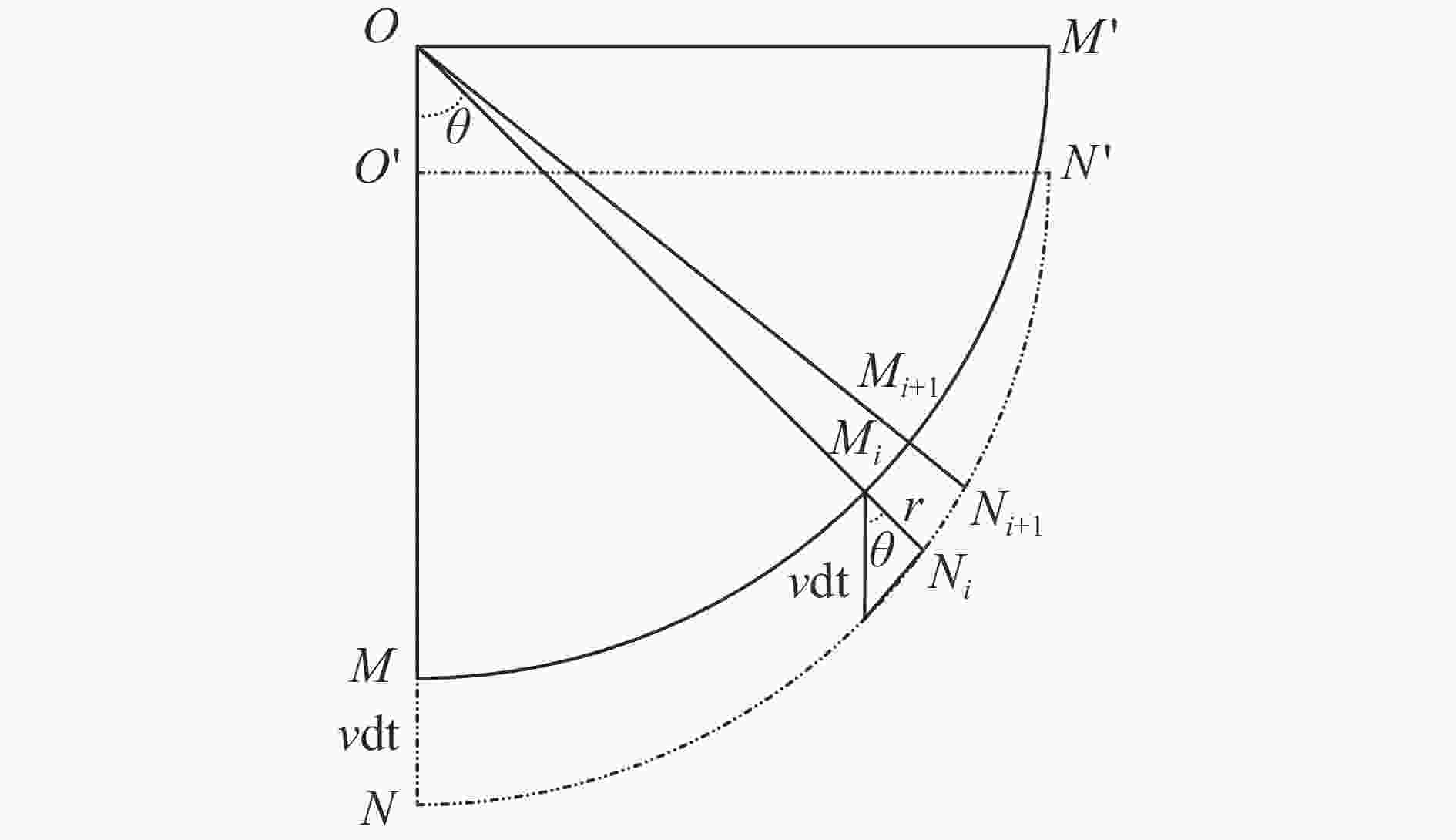
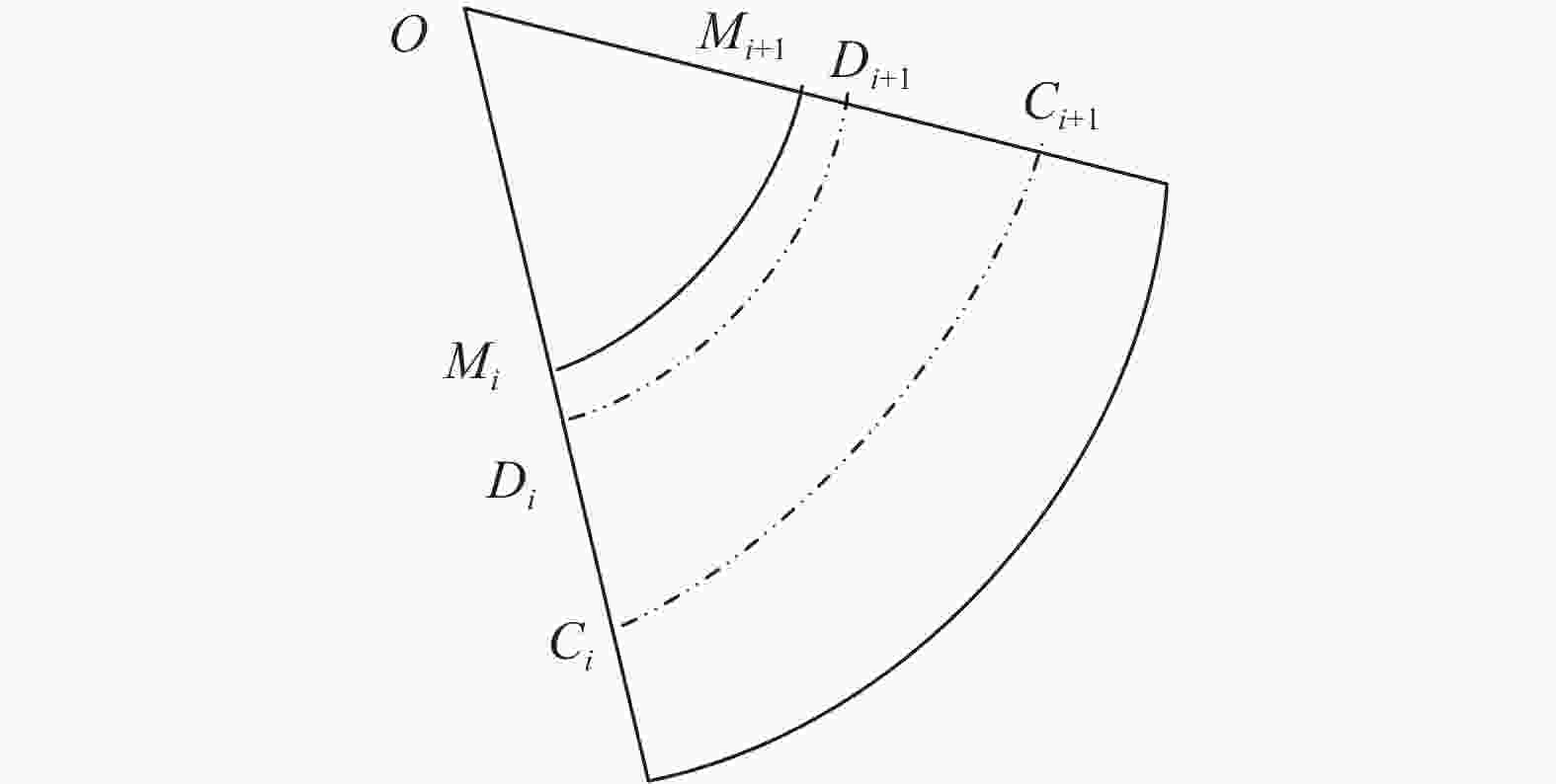
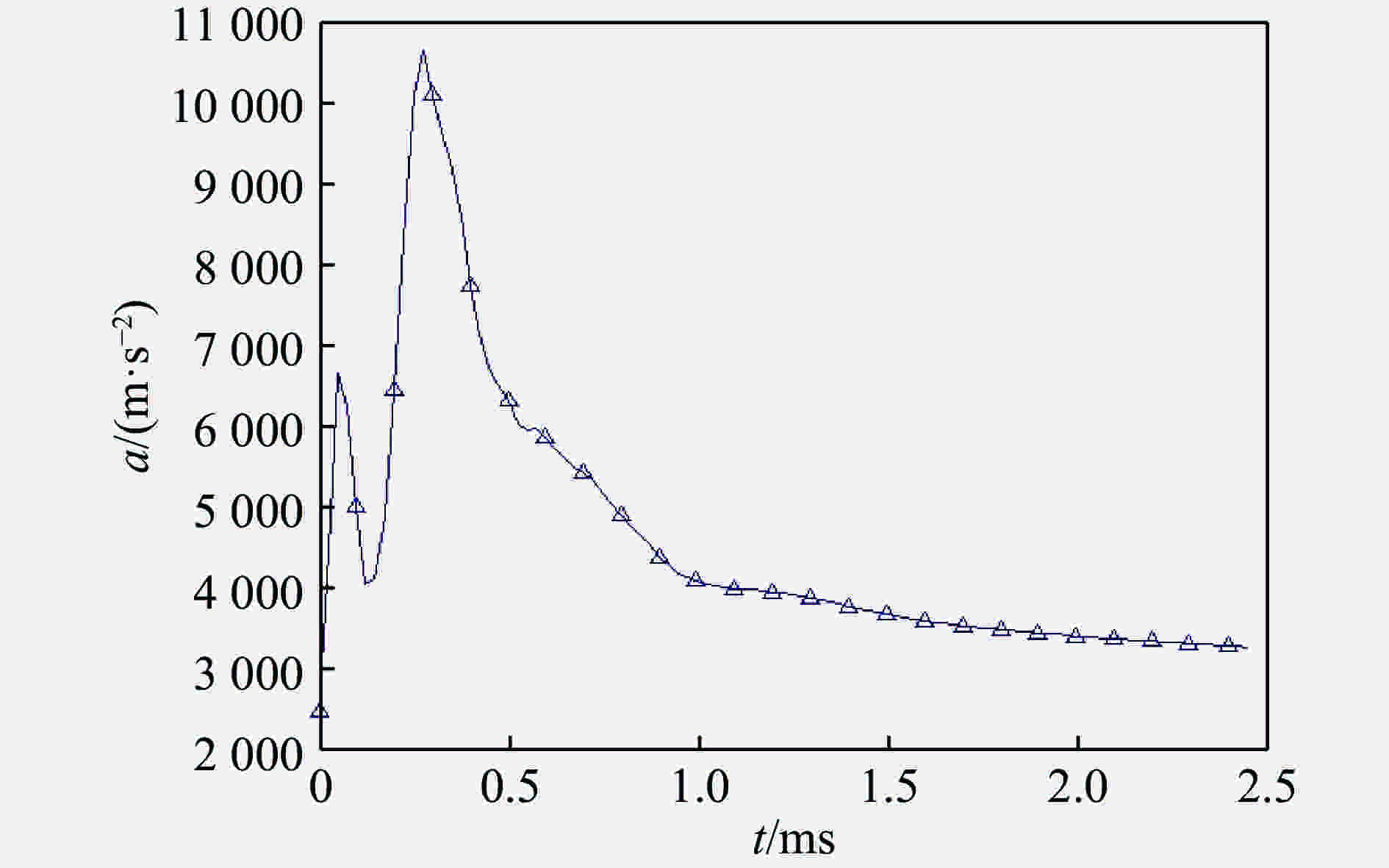
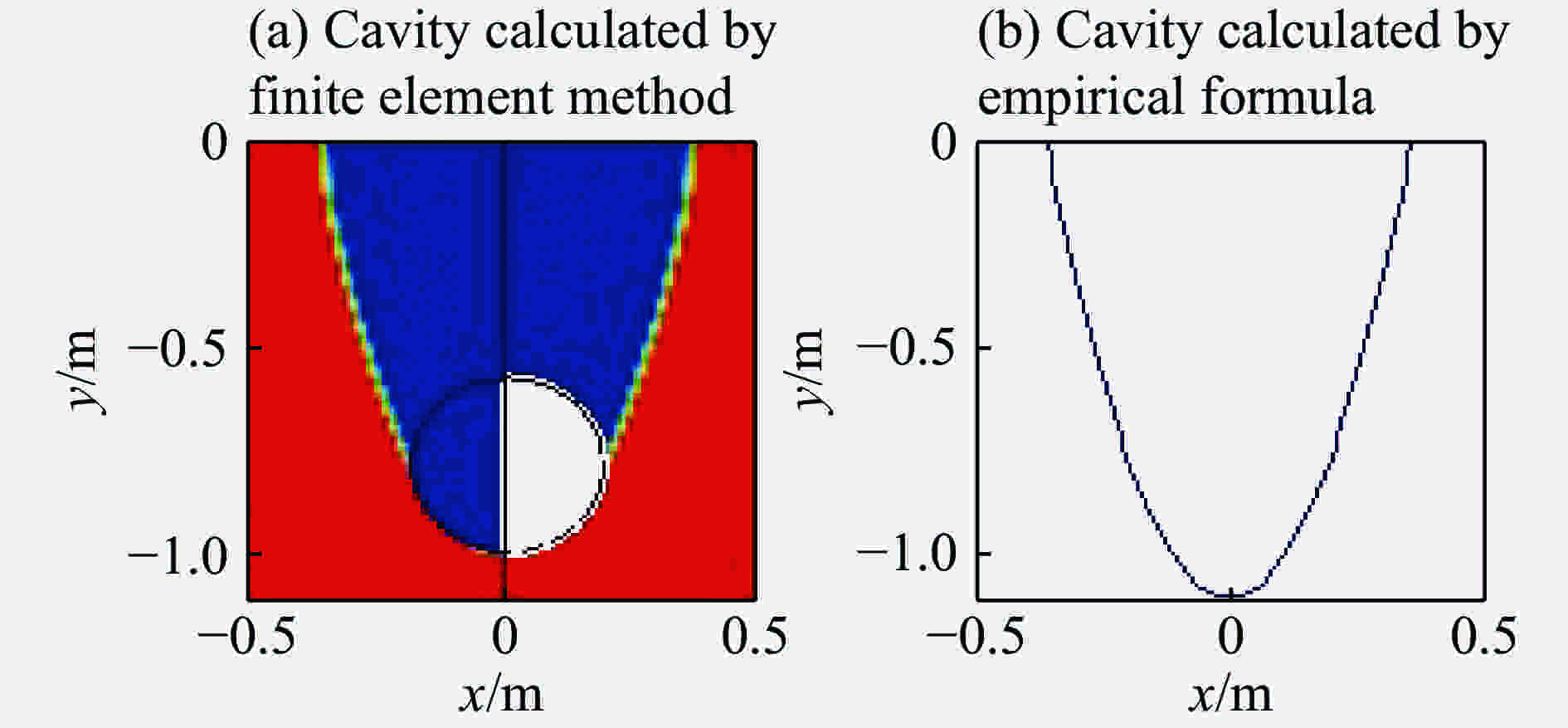
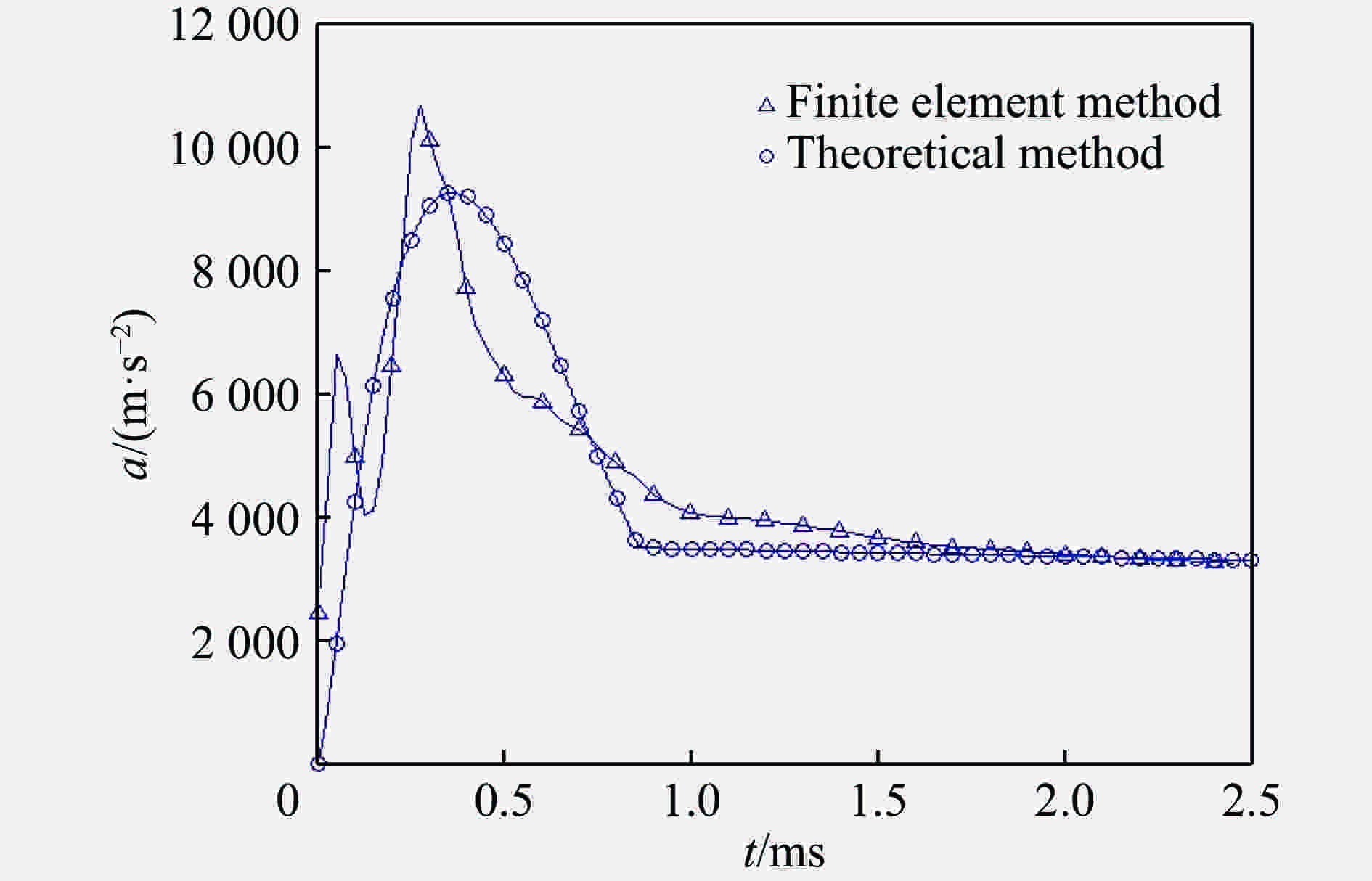
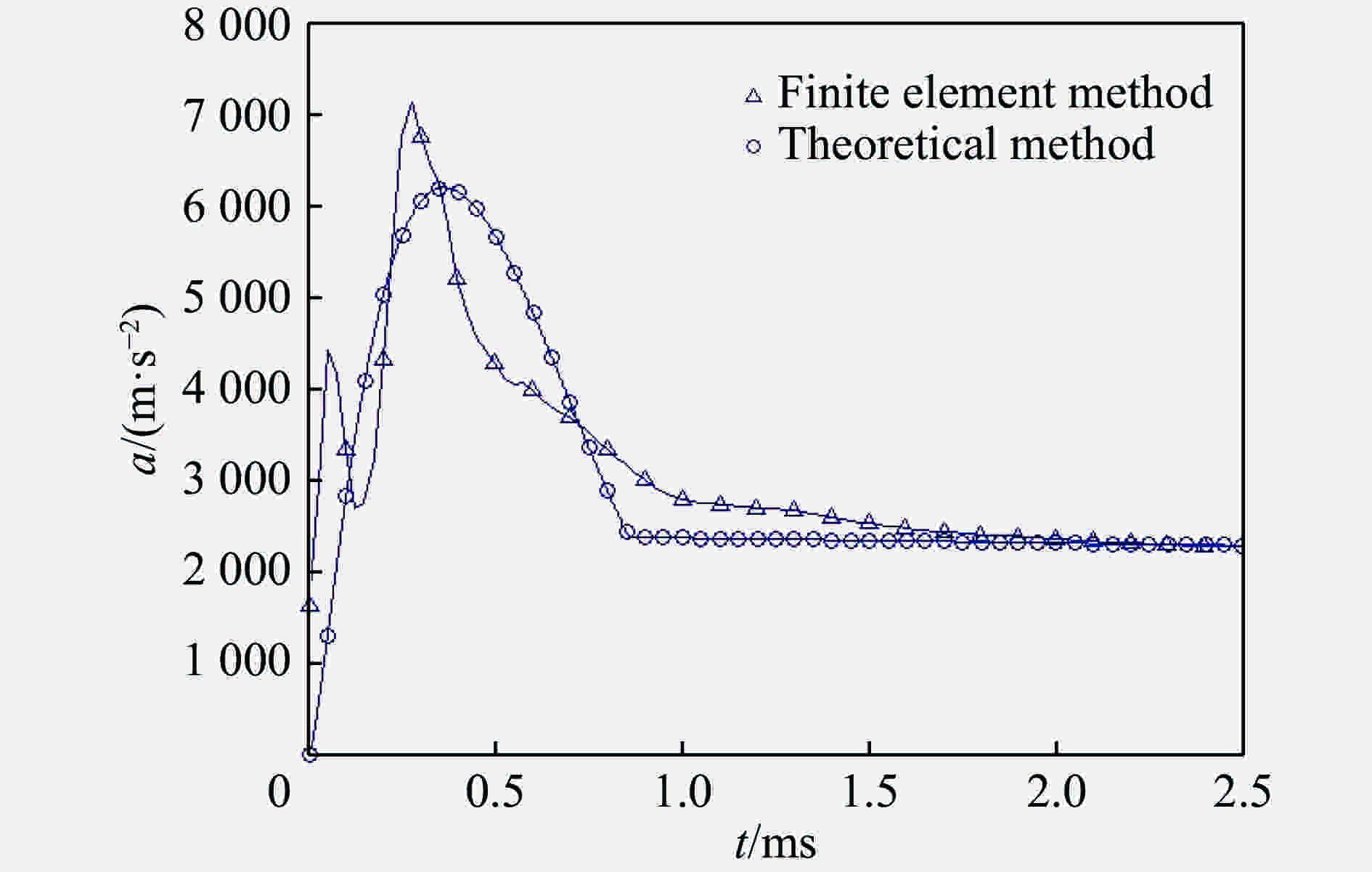
Three-dimensional vertical free high-speed water-entry impact of rigid sphere

1.
Academy of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China
2.
Unit No.91267, Fuzhou 350000, Fujian, China

摘要

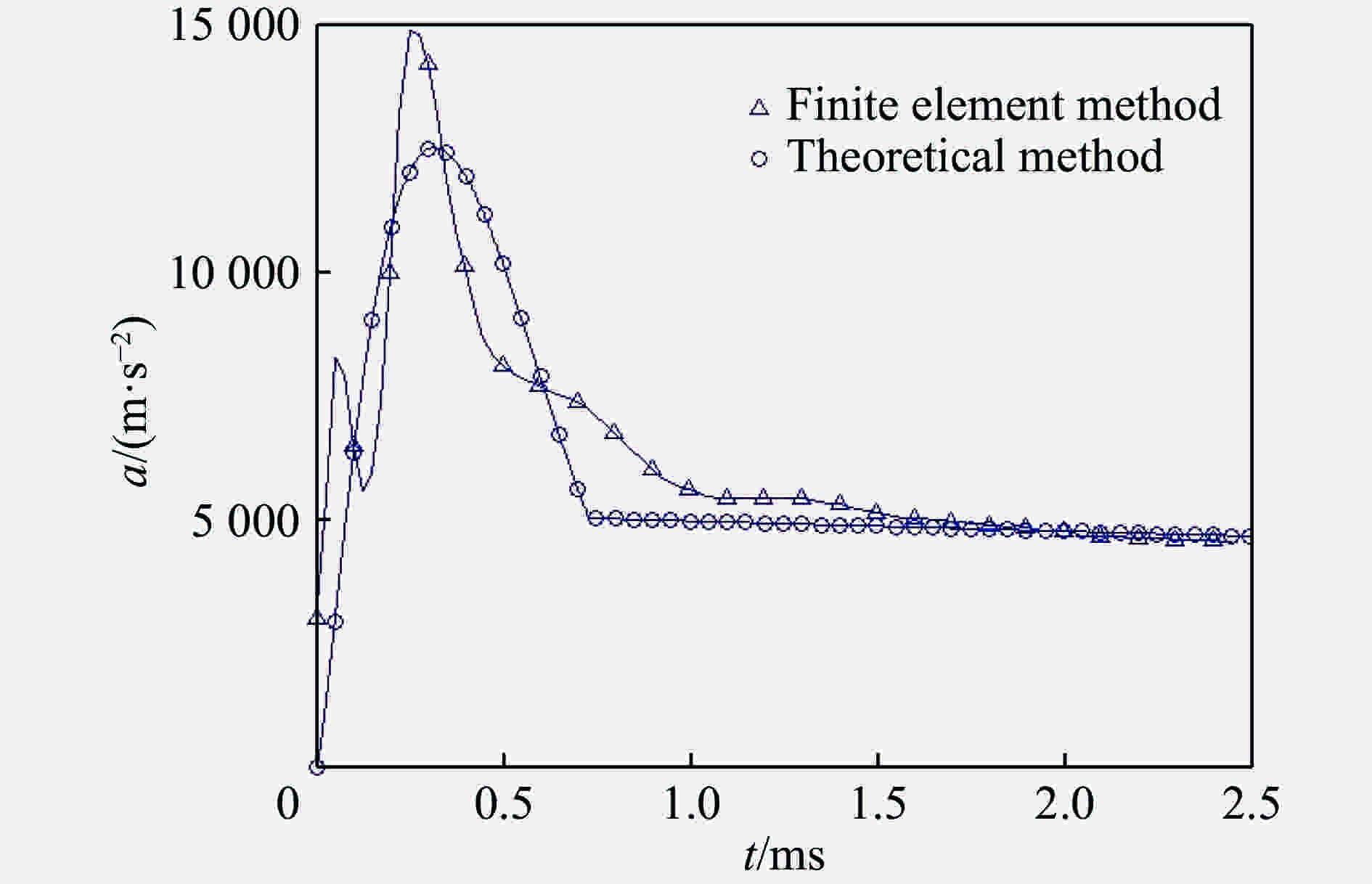
摘要: 入水结构体在从空中弹道转入水下弹道的入水阶段，其周围的流体将呈现出强非线性性质，本文针对传统基于Wagner理论的结构体入水载荷计算模型不能很好描述流体三维流动的情况，基于无黏不可压流体流动模型，考虑流体弹性，采用微元边界运动等效方法对运动边界进行分段分析，计及入水过程中系统的动能损失，根据能量守恒，对刚性球体高速垂直自由入水过程中流体的三维流动进行了理论分析，建立了基于无黏不可压弹性流体的刚性球体垂直高速入水载荷计算模型，并与基于多介质任意拉格朗日欧拉方法的有限元模型进行了对比分析，验证了该方法的可行性。基于此模型，本文进一步分析了入水载荷的影响因素。该方法提供了一种计算结构体垂直高速入水载荷的思路，具有一定的理论意义和工程应用价值。
- 刚性球体 /
- 三维入水 /
- 载荷 /
- 弹性理论 /
- 微元边界运动等效
Abstract: At the initial stage of water entry, the water surrounding of the rigid sphere will show strong nonlinear characteristics. However, there are no exact three-dimensional effects in impact problem within the Wagner theory. Based on the non-viscous incompressible flow model, this paper considered fluid elasticity, used the micro boundary motion equivalent method to analyze the moving boundary, and based on the theory of energy conservation, which considered the loss of kinetic energy, analyzed the three-dimensional flow of the fluid around the rigid sphere during high-speed water-entry vertically, then established the analytical model which can calculate the water-entry impact of rigid sphere, and the analytical model is verified by an FEM model of multi-material ALE method. Base on the analytical model, this paper also analyzed the influencing factors of impact. The analytical model provides a fast algorithm for calculating the high-speed water-entry impact of structure, and has certain theoretical significance and engineering application value.
- rigid sphere /
- three-dimensional water-entry /
- impact /
- theory of fluid elasticity /
- microboundary motion equivalent method

HTML全文

图 1 刚性球体位置示意图

Figure 1. General view of the rigid sphere’s location

下载: 全尺寸图片幻灯片

图 2 球体入水运动示意图

Figure 2. General view of sphere’s micromovement

下载: 全尺寸图片幻灯片

图 3 弧段微元示意图

Figure 3. General view of a microsegmental arc

下载: 全尺寸图片幻灯片

图 4 微元边界运动等效示意图

Figure 4. General view of microboundary’s motion equivalent

下载: 全尺寸图片幻灯片

图 5 微元边界扩张示意图

Figure 5. General view of microsegmental arc’s expansion

下载: 全尺寸图片幻灯片

图 6 有限元模型

Figure 6. Finite element model

下载: 全尺寸图片幻灯片

图 7 球体入水载荷曲线

Figure 7. Water-entry impact curve of the sphere

下载: 全尺寸图片幻灯片

图 8 入水空泡轮廓对比图

Figure 8. Comparison of the cavities

下载: 全尺寸图片幻灯片

图 9 入水载荷对比图

Figure 9. Comparison of water-entry impact

下载: 全尺寸图片幻灯片

图 10 球体质量为391.5 kg时入水载荷对比图

Figure 10. Comparison of water-entry impact when the sphere’s mass is 391.5 kg

下载: 全尺寸图片幻灯片

图 11 入水速度为240 m/s时入水载荷对比图

Figure 11. Comparison of water-entry impact when initial velocity is 240 m/s

下载: 全尺寸图片幻灯片

图 12 入水载荷对比图

Figure 12. Comparison of water-entry impact

下载: 全尺寸图片幻灯片

图 13 入水载荷对比图

Figure 13. Comparison of water-entry impact

下载: 全尺寸图片幻灯片

图 14 入水载荷对比图

Figure 14. Comparison of water-entry impact

下载: 全尺寸图片幻灯片

表 1 入水载荷峰值对比

Table 1. Comparison of the water-entry peak impact

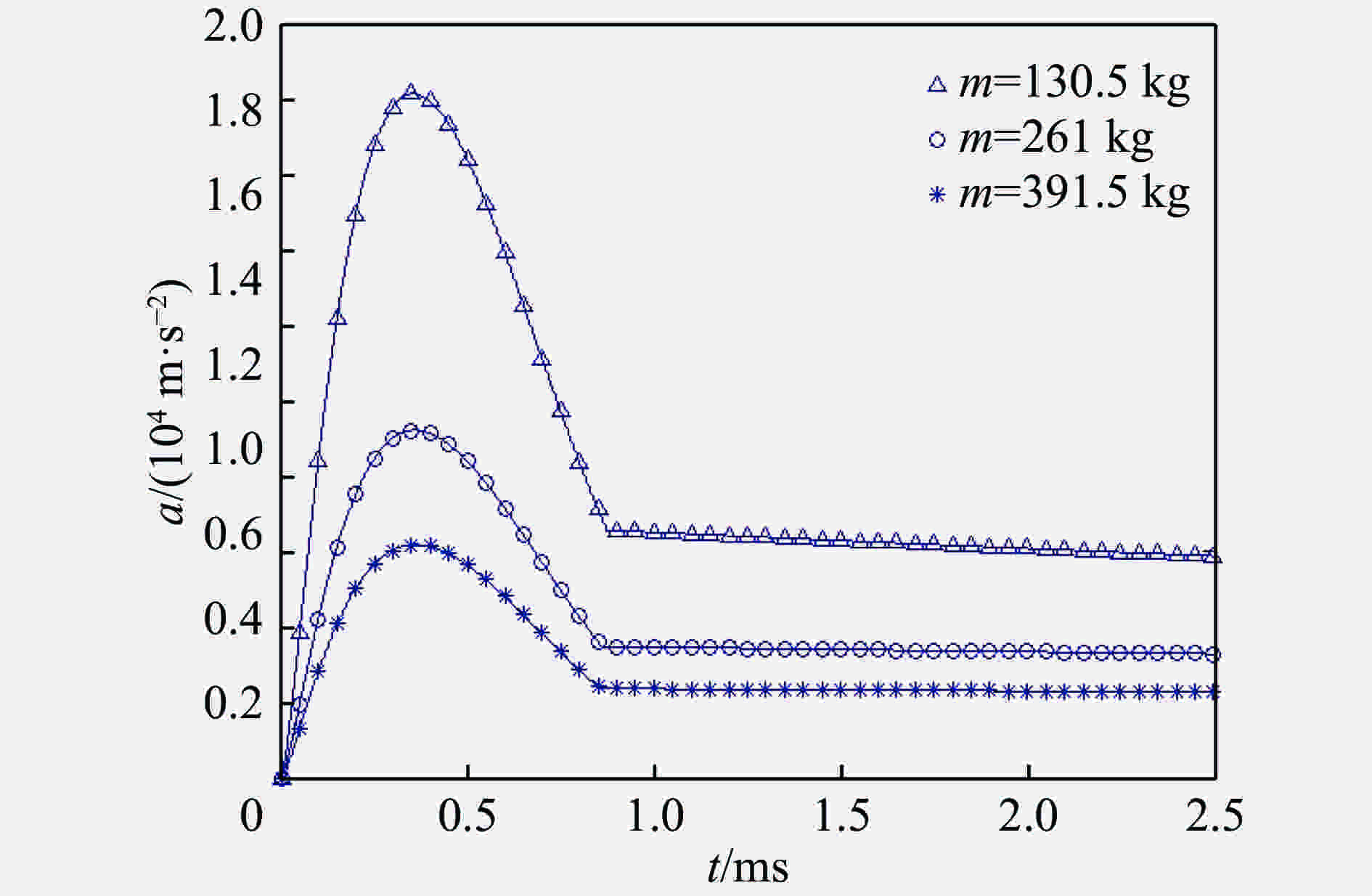
m/kg a_max/(km·s⁻²） (ma_max)/MN

130.5 18.2 2.38
261.0 9.2 2.40
391.5 6.2 2.43

下载: 导出CSV

表 2 入水载荷峰值对比

Table 2. Comparison of the water-entry peak impact

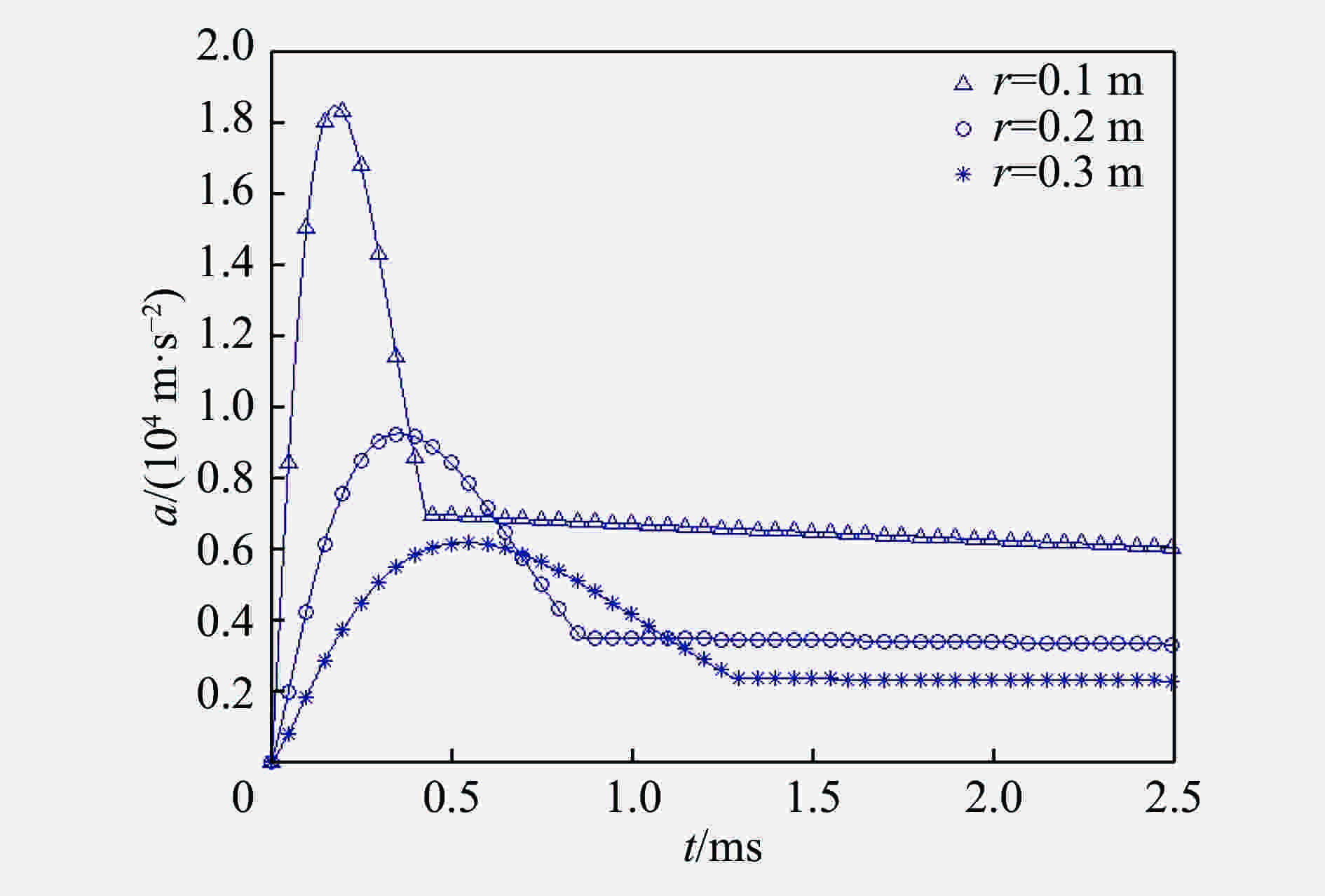
R/m a_max/（km·s⁻²） (Ra_max)/(10² m²·s⁻²)

0.1 18.5 1.85
0.2 9.2 1.84
0.3 6.2 1.86

下载: 导出CSV

表 3 入水载荷峰值对比

Table 3. Comparison of the water-entry peak impact

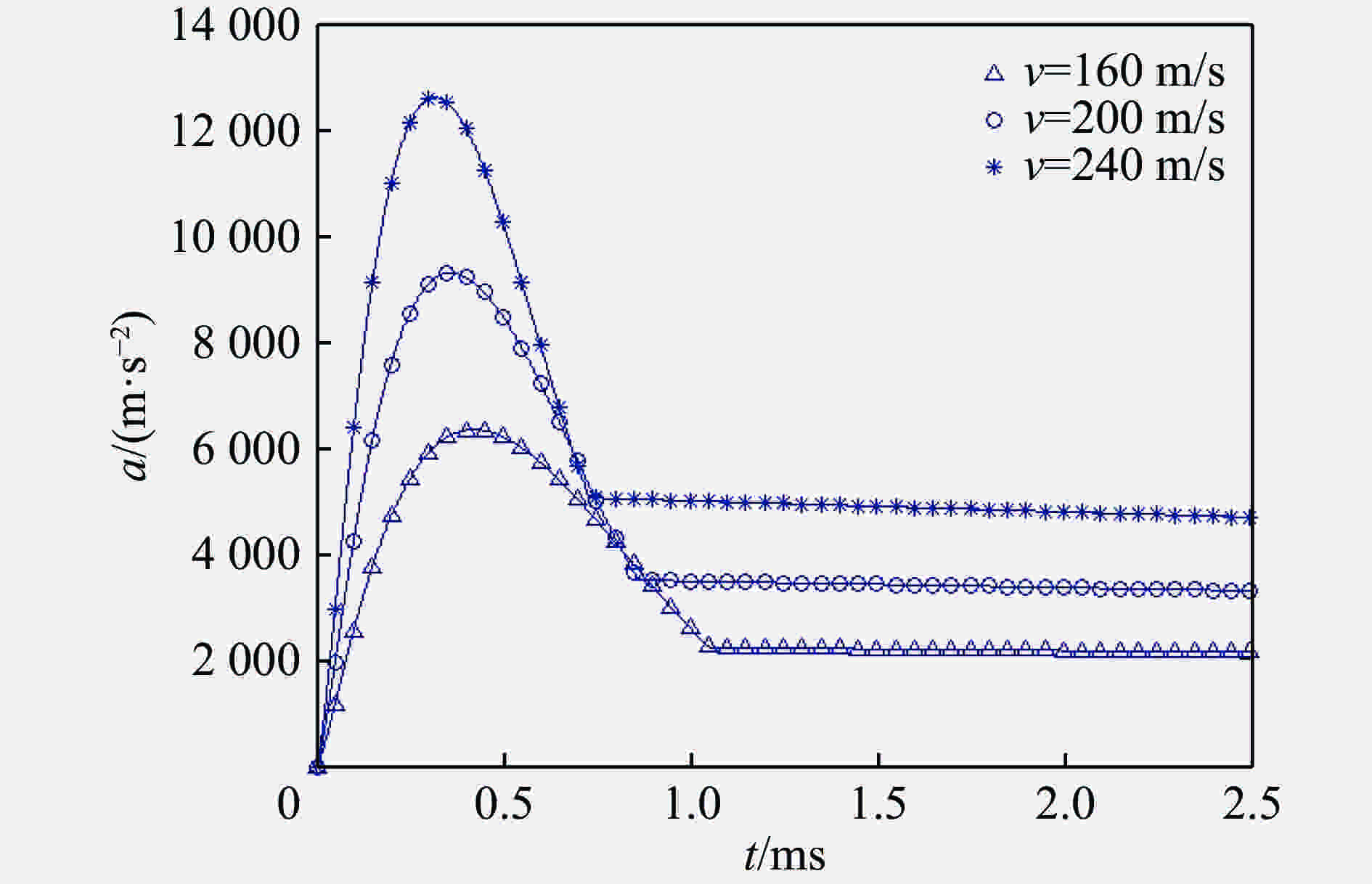
v/（10² m·s⁻¹） a_max/（km·s⁻²） (v²/a_max) /m

1.6 6.3 4.06
2.0 9.2 4.35
2.4 12.5 4.6

下载: 导出CSV

参考文献(20)

[1]	WAGNER V H. Phenomena associated with impacts and sliding on liquid surfaces [J]. Zeitschrift fur Angewandte Mathematik und Mechanik, 1932, 12(4): 193–215. doi: 10.1002/(ISSN)1521-4001
[2]	MAY A, WOODHULL J C. Drag coefficients of steel spheres entering water vertically [J]. Journal of Applied Physics, 1948, 19: 1109–1121. doi: 10.1063/1.1715027
[3]	KOROBKIN A A, PUKHNACHOV V V. Initial stage of water impact [J]. Annual Review of Fluid Mechanics, 1998, 20: 159–185.
[4]	SCOLAN Y M, KOROBKIN A A. Three-dimensional theory of water impact: Part 1: Inverse Wagner problem [J]. Journal of Fluid Mechanics, 2001, 440: 293–326.
[5]	MOHAMMAD J, MAURIZIO P. Water entry of compliant slender bodies: theory and experiments [J]. International Journal of Mechanical Sciences, 2017, 13(59): 1–16.
[6]	宋保维, 杜晓旭, 孟锐, 等. 空投水雷入水冲击力仿真 [J]. 鱼雷技术, 2008, 16(3): 6–12. doi: 10.3969/j.issn.1673-1948.2008.03.002 SONG Baowei, DU Xiaoxu, MENG Rui, et al. Numerical simulation of water-entry impact force for air-launched mine [J]. Torpedo Technology, 2008, 16(3): 6–12. doi: 10.3969/j.issn.1673-1948.2008.03.002
[7]	王永虎, 石秀华, 王鹏, 等. 平头尖拱体斜入水冲击理论建模与仿真 [J]. 鱼雷技术, 2008, 16(1): 14–17. doi: 10.3969/j.issn.1673-1948.2008.01.004 WANG Yonghu, SHI Xiuhua, WANG Peng, et al. Modeling and simulation of oblique water-entry of disk ogive [J]. Torpedo Technology, 2008, 16(1): 14–17. doi: 10.3969/j.issn.1673-1948.2008.01.004
[8]	孙士丽, 吴国雄. 有限水深中非轴对称体斜向入水抨击问题研究 [J]. 水动力学研究与进展, 2013, 28(4): 445–451. SUN Shili, WU Guoxiong. Oblique entry of non-axisymmetric bodies into water of finite depth [J]. Chinese Journal of Hydrodynamics, 2013, 28(4): 445–451.
[9]	王健, 赵庆彬, 陶钢, 等. 火箭撬水刹车高速入水冲击数值模拟 [J]. 爆炸与冲击, 2010, 30(6): 628–632. DOI: 10.11883/1001-1455(2010)06-0628-05. WANG Jian, ZHAO Qingbin, TAO Gang, et al. Numerical simulation on rocket sled water-brake high-speed water-entry impact [J]. Explosion and Shock Waves, 2010, 30(6): 628–632. DOI: 10.11883/1001-1455(2010)06-0628-05.
[10]	马庆鹏, 魏英杰, 王聪, 等. 不同头型运动体高速入水空泡数值模拟 [J]. 哈尔滨工业大学学报, 2014, 46(11): 24–29. doi: 10.11918/j.issn.0367-6234.2014.11.004 MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high-speed water entry cavity of cylinders [J]. Journal of Harbin Institute of Technology, 2014, 46(11): 24–29. doi: 10.11918/j.issn.0367-6234.2014.11.004
[11]	朱珠, 袁绪龙. 柱体高速入水冲击载荷与空泡特性 [J]. 计算机仿真, 2014, 31(3): 29–33. doi: 10.3969/j.issn.1006-9348.2014.03.007 ZHU Zhu, YUAN Xulong. High-speed water-entry impact and cavity characters of cylinder [J]. Computer Simulation, 2014, 31(3): 29–33. doi: 10.3969/j.issn.1006-9348.2014.03.007
[12]	OGER G, DORING M, ALESSANDRINI B, et al. Two-dimensional SPH simulations of wedge water entries [J]. Journal of Computational Physics, 2006, 213: 803–822. doi: 10.1016/j.jcp.2005.09.004
[13]	张伟, 黄威, 任鹏, 等. 高速弹体水平入水产生冲击波特性 [J]. 哈尔滨工业大学学报, 2016, 48(4): 37–41. ZHANG Wei, HUANG Wei, REN Peng, et al. The underwater shock wave characteristics caused by high speed horizontal water entry projectiles [J]. Journal of Harbin Institute of Technology, 2016, 48(4): 37–41.
[14]	王永虎, 石秀华. 入水冲击问题研究的现状与进展 [J]. 爆炸与冲击, 2008, 28(3): 276–282. DOI: 10.11883/1001-1455(2008)03-0276-07. WANG Yonghu, SHI Xiuhua. Review on research and development of water-entry impact problem [J]. Explosion and Shock Waves, 2008, 28(3): 276–282. DOI: 10.11883/1001-1455(2008)03-0276-07.
[15]	秦红德, 赵林岳, 申静. 入水冲击问题综述 [J]. 哈尔滨工业大学学报, 2011, 43: 152–157. QIN Hongde, ZHAO Linyue, SHEN Jing. Review of water entry problem [J]. Journal of Harbin Institute of Technology, 2011, 43: 152–157.
[16]	LEE M, LONGORIA R G, WILSON D E. Ballistic waves in high-speed water entry [J]. Journal of Fluids and Structures, 1997, 11: 819–844. doi: 10.1006/jfls.1997.0103
[17]	马庆鹏, 魏英杰, 王聪, 等. 锥头圆柱体高速入水空泡数值模拟 [J]. 北京航空航天大学学报, 2014, 40(2): 204–209. MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high-speed water-entry cavity of cone cylinder [J]. Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 204–209.
[18]	何春涛. 典型运动体入水过程多相流动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2012: 33−36. HE Chuntao. Study on multiphase flow of typical body during water entry [D]. Harbin: Harbin Institute of Technology, 2012: 33−36.
[19]	MAY A. Water entry and the cavity-running behavior of missiles: ADA020429 [R]. Maryland: White Oak Laboratory, 1975.
[20]	顾建农, 张志宏, 王冲, 等. 旋转弹头水平入水空泡及弹道的实验研究 [J]. 兵工学报, 2012, 33(5): 540–544. GU Jiannong, ZHANG Zhihong, WANG Chong, et al. Experimental research for cavity and ballistics of a rotating bullet entraining water levelly [J]. Acta Armamentarii, 2012, 33(5): 540–544.