Failure behavior and energy release of Zr-based amorphous alloy under dynamic compression
-
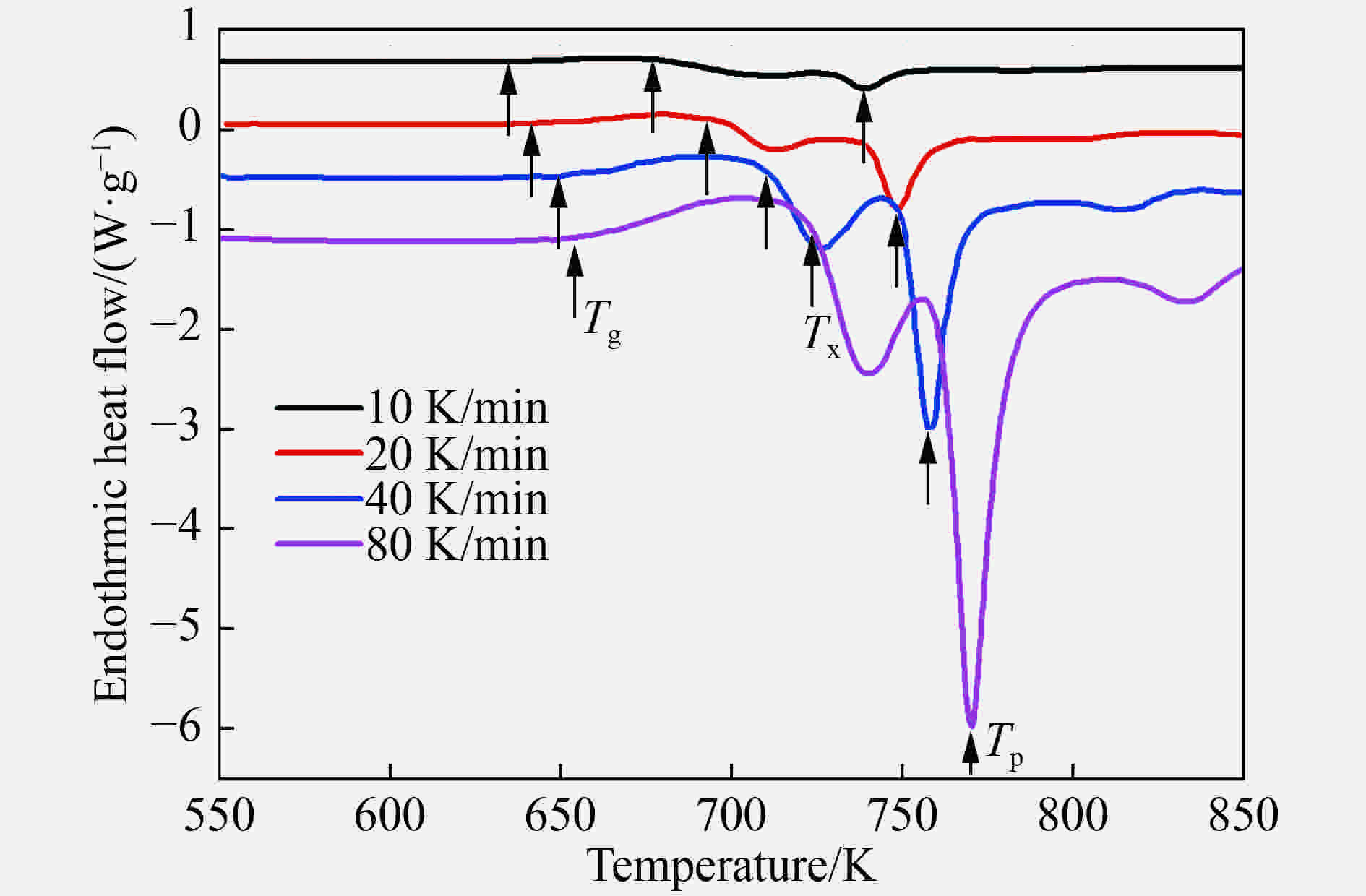
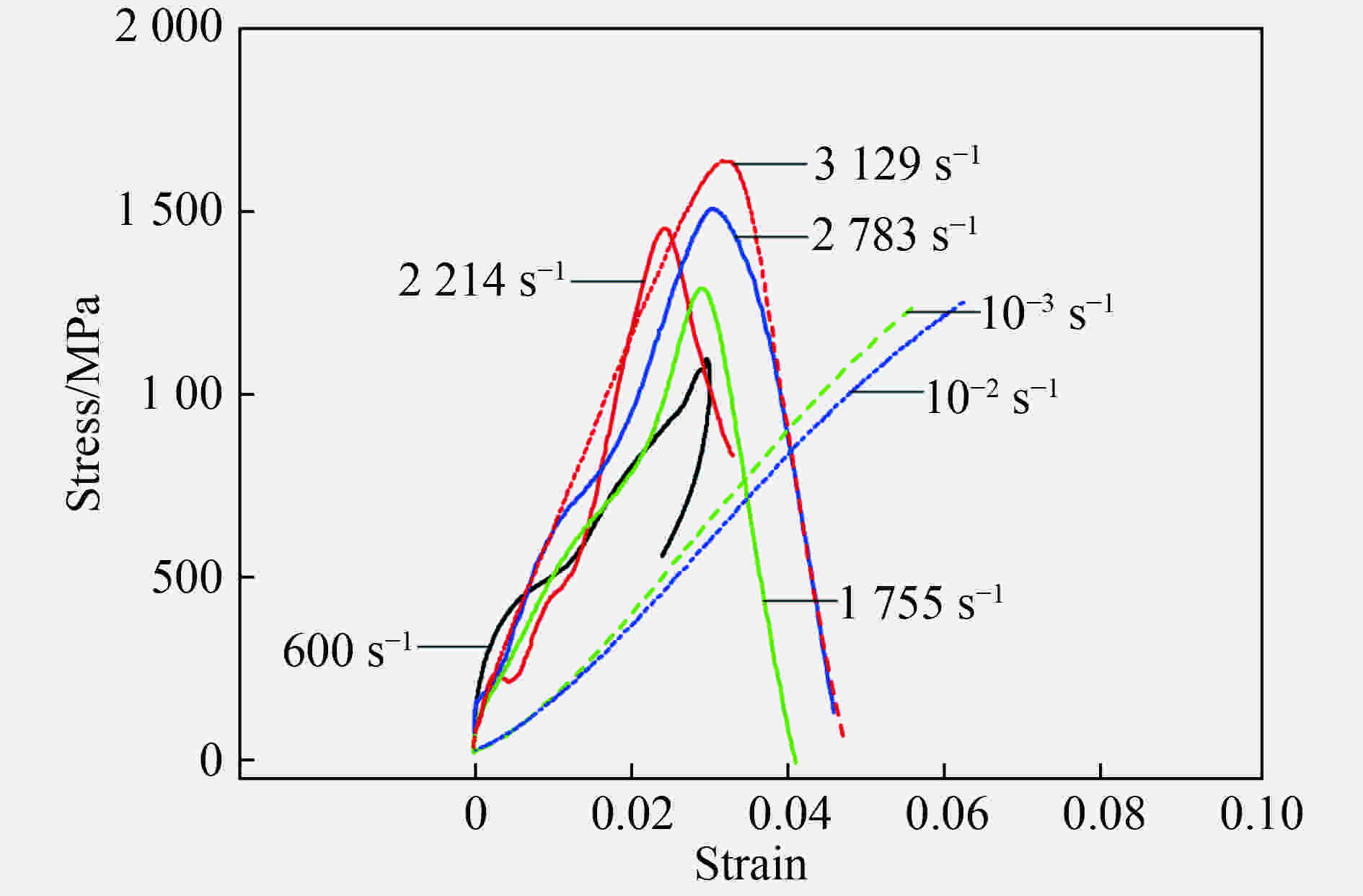
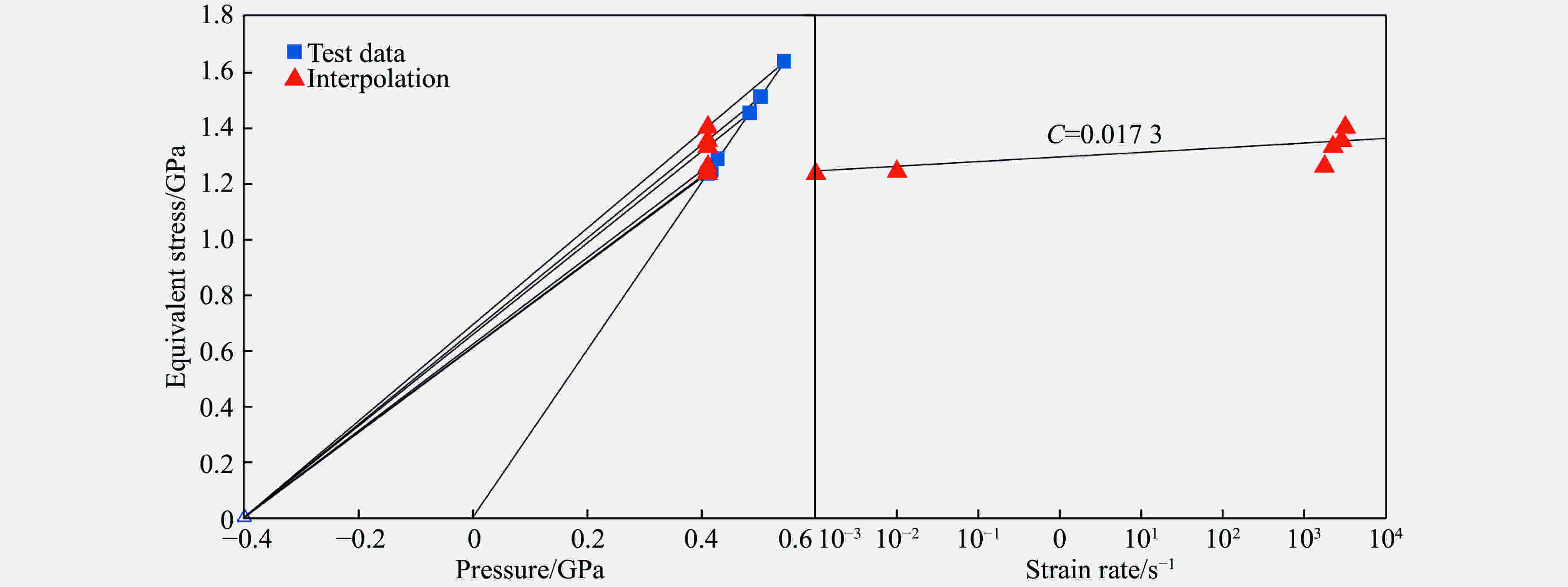
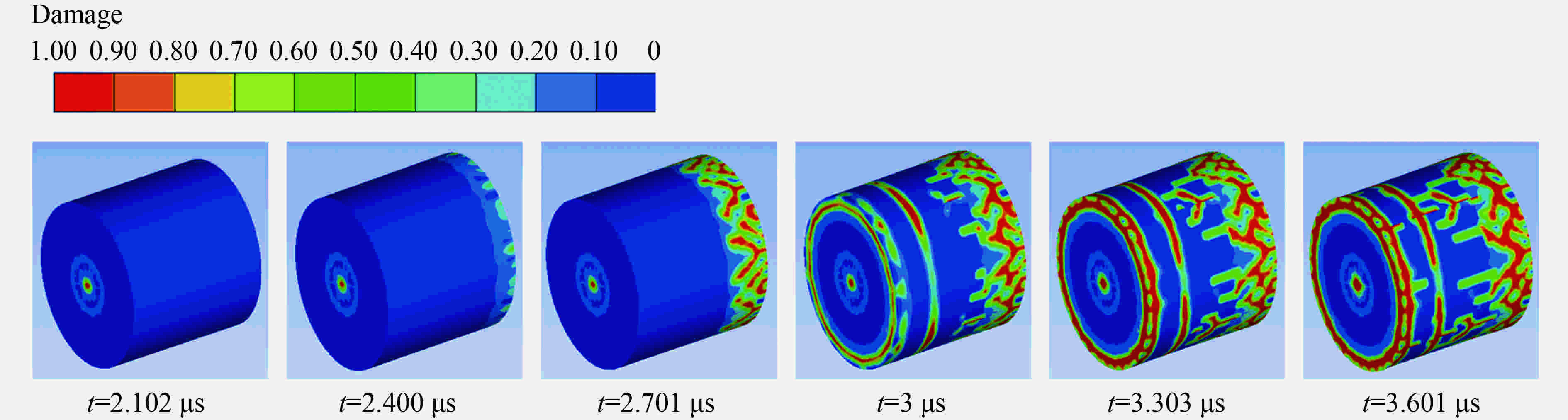
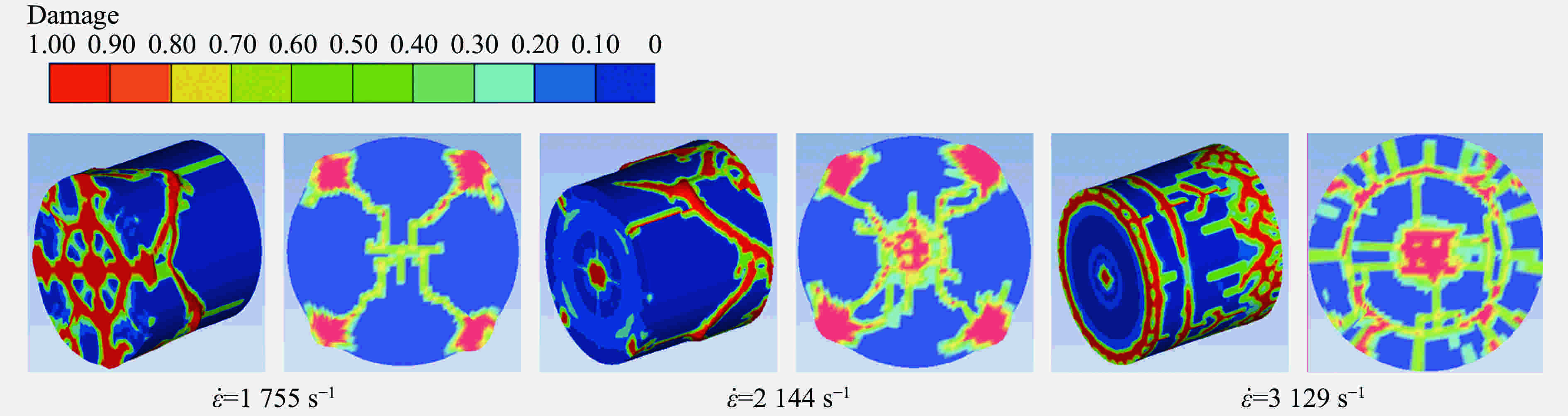
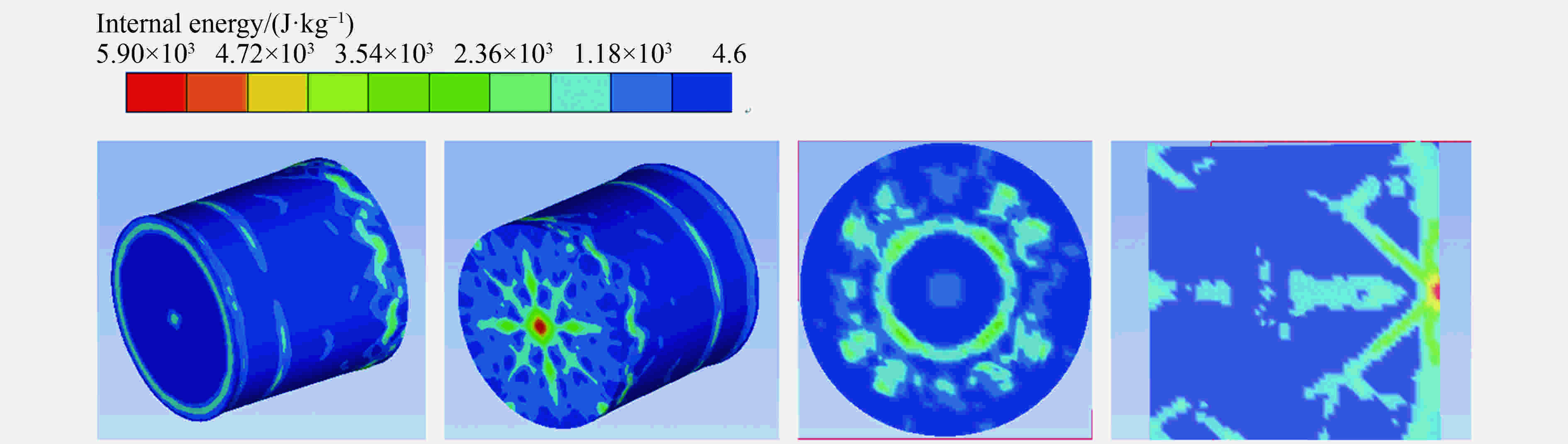
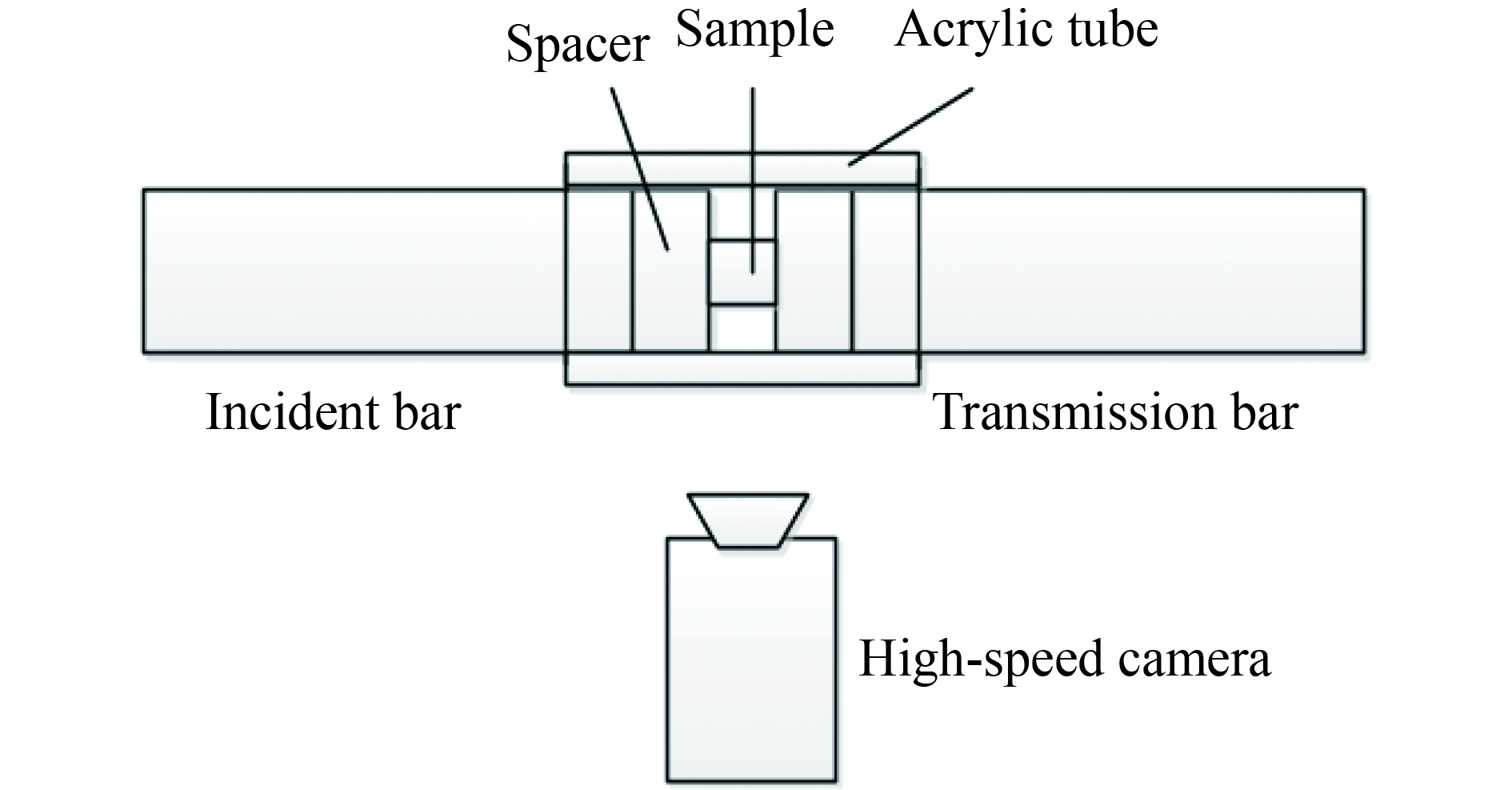
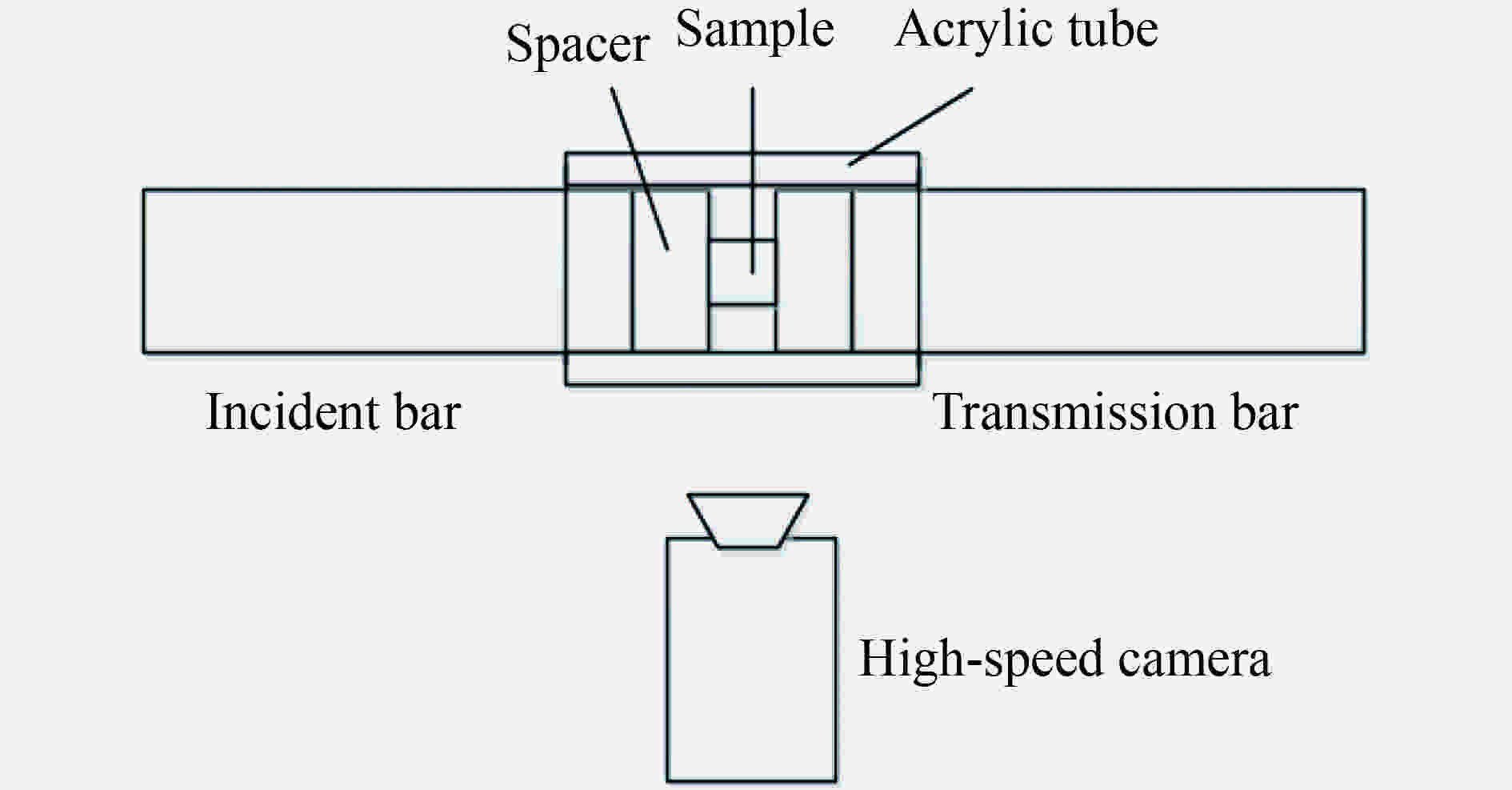
摘要: 为研究Zr基非晶合金动态压缩条件下的失效释能机理，采用力学试验机、霍普金森杆、高速摄影、差示扫描量热分析（differential scanning calorimetry, DSC）、扫描电镜（scanning electron microscope，SEM）等，得到了材料应力应变曲线、高速摄影图像、失效式样微观形貌及DSC曲线，根据实验数据计算了材料的晶化激活能，并拟合了材料的JH-2（Johnson-Holmquist II）模型，对材料动态失效过程进行有限元数值模拟。实验结果表明，压缩条件下材料为脆性断裂，断口处观察到典型的脉状纹样及液滴状结构，材料失效过程伴随着释能现象；数值模拟结果表明，材料裂纹局部的瞬时内能大于材料晶化激活能。动态压缩下材料的失效释能机理即为材料破碎释放储存的弹性势能，并导致材料局部晶化释能，释能强度与应变率成正相关。Abstract: To study the mechanism of failure behavior and energy release mechanism of Zr-based amorphous alloys, Instron machine, split hopkinson bar, high-speed photography, DSC and SEM are used to achieve the stress-strain curves at low strain rate, stress-strain curves at high strain rate, failure processes, DSC curves and failure morphologies, respectively. The crystallization enthalpy is obtained from DSC curves. The stress-strain curves are fitted by the Johnson-Holmquist II model, and the finite element method using this model is executed to simulate the failure process of material under dynamic compression. The experimental results suggest that the material fractures brittle under compression. Typical vein-like pattern is observed at the fracture surface of the material. The energy releasing occurs simultaneously with the material failure. The simulation results reveal that the internal energy of local crack is higher than crystallization enthalpy of the material. The energy release of Zr-based amorphous alloys results in the elastic potential energy and crystallization energy released by the material with instantaneous crack. The strength of energy release is in direct proportion to strain rates.
-
Key words:
- Zr-based amorphous alloys /
- dynamic compression /
- failure /
- energy release /
- high-speed imaging
-
图 2 不同升温速率下热流随温度变化曲线
Figure 2. Curves of endothermic heat flow as a function of temperature at different heating rates
图 3 材料压缩应力应变曲线
Figure 3. Stress-strain curves of Zr-based amorphous alloys in compression
图 7 材料动态压缩高速摄影图像
Figure 7. High-speed photography of material under dynamic compression
图 9 3 129 s−1应变率下材料损伤云图
Figure 9. Damage maps of material under the strain rate of of 3 129 s−1
表 1 材料的JH-2材料模型参数
Table 1. JH-2 model constants of the material
材料 K1/GPa K2 /GPa K3/GPa D1 D2 ZrTiNiCuBe 114.3 268.5 1 386 0.21 1.75 材料 A B C M N ZrTiNiCuBe 1.162 0.258 0.017 3 0.59 0.829 
下载: 导出CSV
-
[1] TOGO H, ZHANG Y, KAWAMURA Y, et al. Properties of Zr-based bulk metallic glass under shock compression [J]. Materials Science and Engineering A, 2007, 449–451: 264–268. DOI: 10.1016/j.msea.2006.02.431. [2] MATTERN N, KUHN U, HERMANN H, et al. Thermal behavior and glass transition of Zr-based bulk metallic glasses [J]. Materials Science and Engineering A, 2004, 375−377: 351–354. DOI: 10.1016/j.msea.2003.10.125. [3] QIAO J W, ZHANG Y, LI J H, et al. Strain rate response of a Zr-based composite fabricated by Bridgman solidification [J]. International Journal of Minerals, Metallurgy and Materials, 2010, 17(2): 214–219. DOI: 10.1007/s12613-010-0216-9. [4] ZHANG Q S, ZHANG W, XIE G Q, et al. Synthesis, structure and mechanical properties of Zr-Cu-based bulk metallic glass composites [J]. International Journal of Minerals, Metallurgy and Materials, 2010, 17(2): 208–213. DOI: 10.1007/s12613-010-0215-x. [5] LIU C, HEATHERLY L, HORTON J, et al. Test environments and mechanical properties of Zr-base bulk amorphous alloys [J]. Metallurgy Materials Transaction A, 1998, 29: 1811–1820. DOI: 10.1007/s11661-998-0004-6. [6] DAI L H, BAI Y L. Basic mechanical behaviors and mechanics of shear banding in BMGs [J]. International Journal of Impact Engineering, 2008, 35: 704–716. DOI: 10.1016/j.ijimpeng.2007.10.007. [7] BATTEZZATI L, BALDISSIN D. Quantitative evaluation of length scales for temperature rise in shear bands and for failure of metallic glasses [J]. Scripta Materialia, 2008, 59: 223–226. DOI: 10.1016/j.scriptamat.2008.03.016. [8] 潘念侨. Zr基非晶合金材料本构关系及其释能效应研究[D]. 南京: 南京理工大学, 2016: 53−71. [9] DAI L H, YAN M, LIU L F, et al. Adiabatic shear banding instability in bulk metallic glasses [J]. Applied Physics Letters, 2005, 87: 141916 -1–14916-32005. DOI: 10.1063/1.2067691. [10] JIANG M Q, LING Z, MENG J X, et al. Energy dissipation in fracture of bulk metallic glasses via inherent competition between local softening and quasi-cleavage [J]. Philosophical Magazine, 2008, 88(3): 407–426. DOI: 10.1080/14786430701864753. [11] JIANG W H, LIAO H H, LIU F X, et al. Rate-dependent temperature increases in shear bands of a bulk-metallic glass [J]. Metallurgical and Materials Transactions A, 2008, 39(8): 1822–1830. DOI: 10.1007/s11661-007-9321-4. [12] WANG J G, PAN Y, SONG S X, et al. How hot is a shear band in a metallic glass? [J]. Materials Science and Engineering A, 2016, 651: 321–331. DOI: 10.1016/j.msea.2015.10.125. [13] WRIGHT W J, BYER R R, GU X J. High-speed imaging of a bulk metallic glass during uniaxial compression [J]. Applied Physics Letters, 2013, 102: 241920. DOI: 10.1063/1.4811744. [14] 李刚. Zr基非晶合金激光熔覆与诱导自蔓延合成[D]. 大连: 大连理工大学, 2003: 11−15. [15] JIANG M Q, WEI Y P, WILDE G, et al. Explosive boiling of a metallic glass superheated by nanosecond pulse laser ablation [J]. Applied Physics Letters, 2015, 106: 021904–1. DOI: 10.1063/1.4905928. [16] WANG C T, HE Y, JI C, et al. Investigation on shock-induced reaction characteristics of a Zr-based metallic glass [J]. Intermatellics, 2018, 93: 383–388. DOI: 10.1016/j.intermet.2017.11.004. [17] FAN Z J, ZHENG Z Y, JIAO Z B. Compressive fracture characteristics of Zr-based bulk metallic glass [J]. Science China Physics, Mechanics and Astronomy, 2016, 53(5): 823–827. DOI: 10.1007/s11433-010-0154-6. [18] NOWAK S, OCHIN P, PASKO A, et al. Mechanical behavior of Zr-based bulk metallic glasses [J]. Strength of Materials, 2008, 40(1): 154–157. DOI: 10.1007/s11223-008-0040-x. [19] JOHNSON G R, HOLMQUIST T J. Response of boron carbide subjected to large strains, high strain rates, and high pressures [J]. Journal of Applied Physics, 1999, 85(12): 8060–8073. DOI: 10.1063/1.370643. [20] WANG W H, LI F Y, PAN M X, et al. Elastic property and its response to pressure in a typical bulk metallic glass [J]. Acta Materialia, 2004, 52: 715–719. DOI: 10.1016/j.actamat.2003.10.008. [21] WANG W H, WEN P, WANG L M, et al. Equation of state of bulk metallic glasses studied by an ultrasonic method [J]. Applied Physics Letters, 2004, 24: 3947–3949. DOI: 10.1063/1.1426272. [22] 石永相. 多元非晶合金含能材料药型罩应用研究[D]. 石家庄: 陆军工程大学, 2017: 35−46. [23] HOLMQUIST T J, TEMPLETON D W, BISHNOI K D. Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications [J]. International Journal of Impact Engineering, 2001, 25: 211–231. DOI: 10.1016/S0734-743X(00)00046-4. 期刊类型引用(13)
1. 眭明斌，郭寻，王本鹏，邢飞，张一博，曹泽凝，覃莒铭，曹堂清，薛云飞. 基于SHPB的含能结构材料冲击释能特性测试系统设计. 实验技术与管理. 2025(02): 59-66 . 
百度学术2. 焦晓龙，王媛婧，吴宗娅，徐豫新. 内衬结构对活性破片高速驱动影响规律研究. 振动与冲击. 2024(04): 230-238 . 百度学术3. 罗锐恒，智小琦，张姚瑶. Zr基非晶合金反应材料的力学性能与冲击烧蚀特性. 金属功能材料. 2023(03): 83-92 . 百度学术4. 侯先苇，张先锋，熊玮，谈梦婷，刘闯，戴兰宏. 活性无序合金冲击的释能特性及在毁伤元中应用研究进展. 爆炸与冲击. 2023(09): 4-42 . 
本站查看5. 郭志平，王飞，姜波，张杰，程波，王传婷，何勇. ZrCuAlNi合金的Taylor撞击断裂行为研究. 兵器装备工程学报. 2022(05): 185-190 . 百度学术6. 张玉令，施冬梅，张云峰，刘国庆，甄建伟. W骨架/Zr基非晶合金复合材料破片侵彻能力与后效研究. 爆炸与冲击. 2021(05): 58-66 . 本站查看7. 邓晶鑫，胡会娥，苏小红，李瑜. 钨颗粒增强锆基非晶复材弹侵彻行为的数值模拟. 兵器装备工程学报. 2021(05): 173-179 . 百度学术8. 张云峰，罗兴柏. Zr基非晶合金破片的侵彻破碎反应机理. 兵器装备工程学报. 2021(06): 133-139 . 百度学术9. 孟元沛，郭志平，王传婷，何勇，何源，胡雪冰. ZrCuAlNiNb非晶合金的Taylor撞击断裂行为研究. 西北工业大学学报. 2021(06): 1296-1303 . 百度学术10. 张云峰，罗兴柏，刘国庆，施冬梅. Zr基非晶合金JH-2模型的构建及应用. 爆炸与冲击. 2020(07): 64-76 . 本站查看11. 尚春明，施冬梅，张云峰，徐雪涛. Zr基非晶合金毁伤研究进展. 兵器装备工程学报. 2020(07): 182-186 . 百度学术12. 何丽灵，张方举，颜怡霞，谢若泽，徐艾民，周燕良. Ti-6Al-4V弹体破坏模式对冲击反应的影响研究. 爆炸与冲击. 2020(12): 58-69 . 本站查看13. 尚春明，施冬梅，李文钊，石永相，徐雪涛. Zr基非晶合金燃烧热测试方法. 兵器装备工程学报. 2019(08): 193-197 . 百度学术其他类型引用(4)
-
百度学术
图(11) / 表(1)
计量
- 文章访问数: 6204
- HTML全文浏览量: 1609
- PDF下载量: 77
- 被引次数: 17