水下爆炸冲击波载荷作用下冰层破碎特性及其影响因素

王莹; 肖巍; 姚熊亮; 秦业志

doi:10.11883/bzycj-2018-0141

水下爆炸冲击波载荷作用下冰层破碎特性及其影响因素

doi: 10.11883/bzycj-2018-0141

哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001

基金项目: 国家自然科学基金（51509228，51779056）

详细信息

作者简介:
王　莹（1990－　），女，博士研究生，wangying1990@hrbeu.edu.cn

通讯作者:
肖　巍（1988－　），男，博士，讲师，wxiao@hrbeu.edu.cn

中图分类号: O382.1
计量
- 文章访问数: 4865
- HTML全文浏览量: 2187
- PDF下载量: 114
- 被引次数: 12
出版历程
- 收稿日期: 2018-04-26
- 修回日期: 2018-07-13
- 网络出版日期: 2019-07-25
- 刊出日期: 2019-07-01

Fragmentation of ice cover subjected to underwater explosion shock wave load and its influence factors

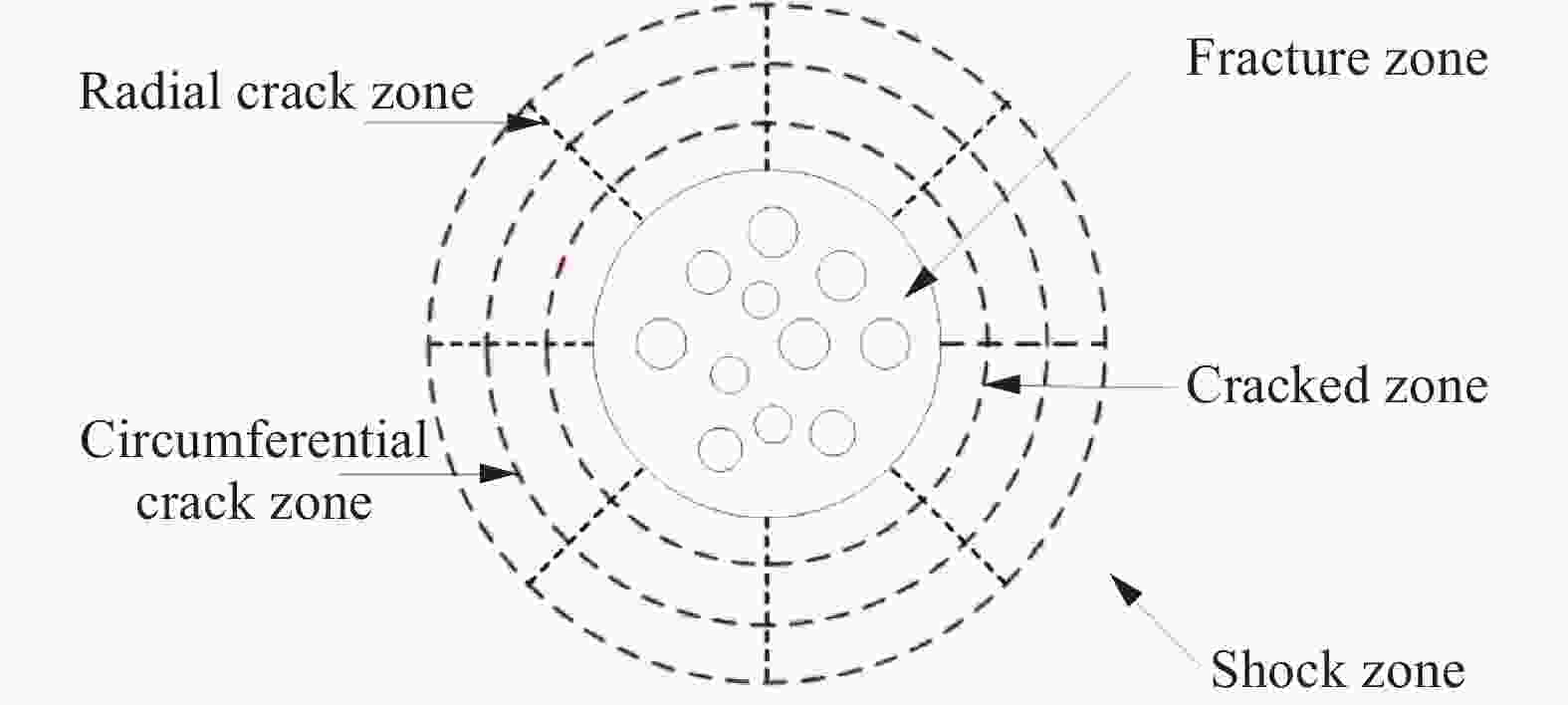
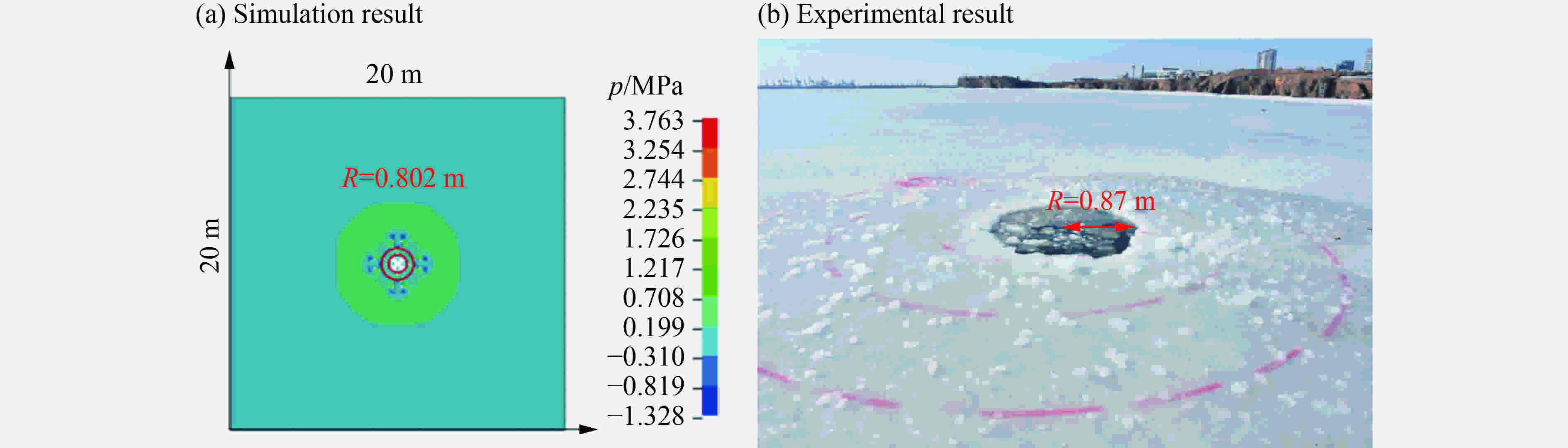
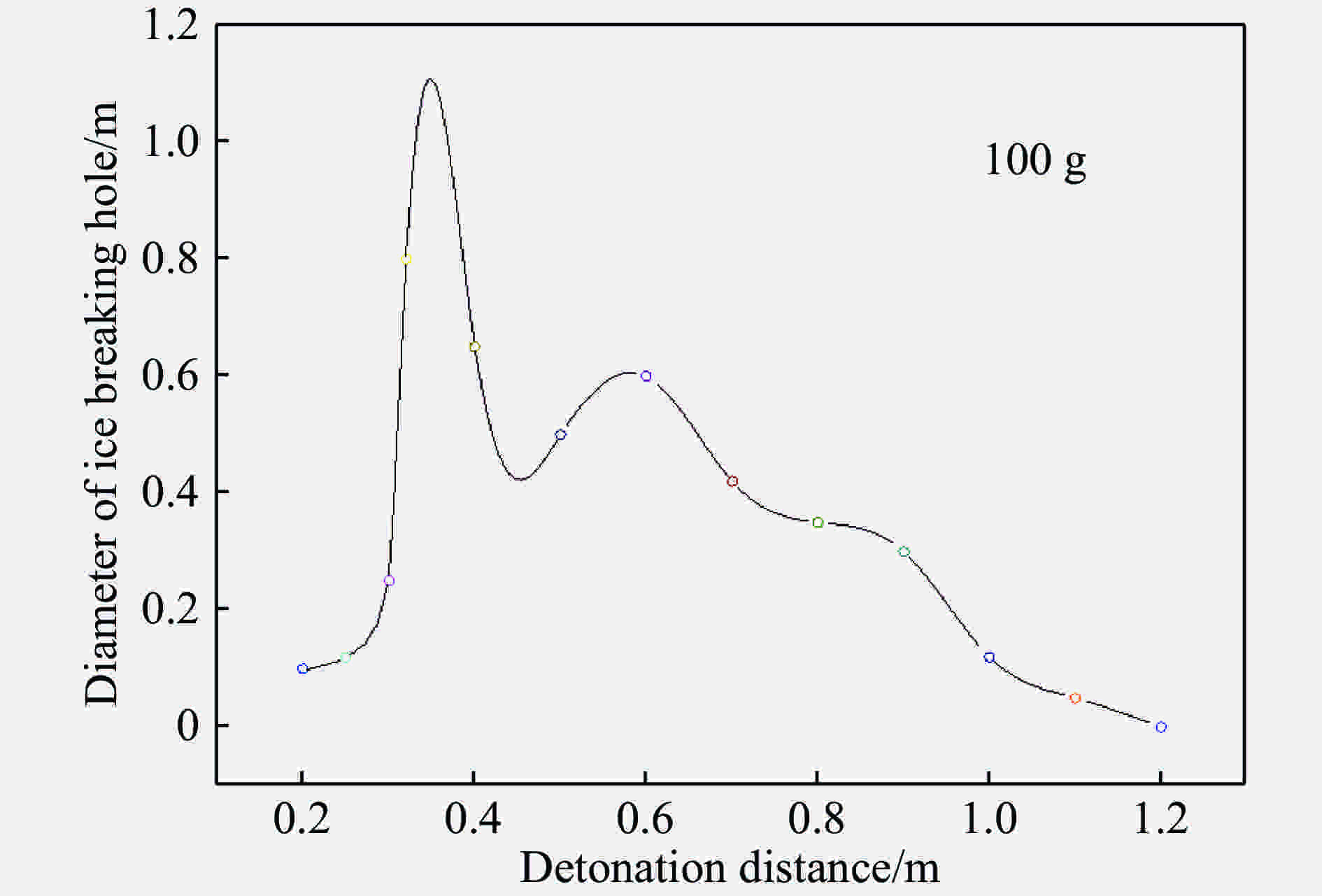
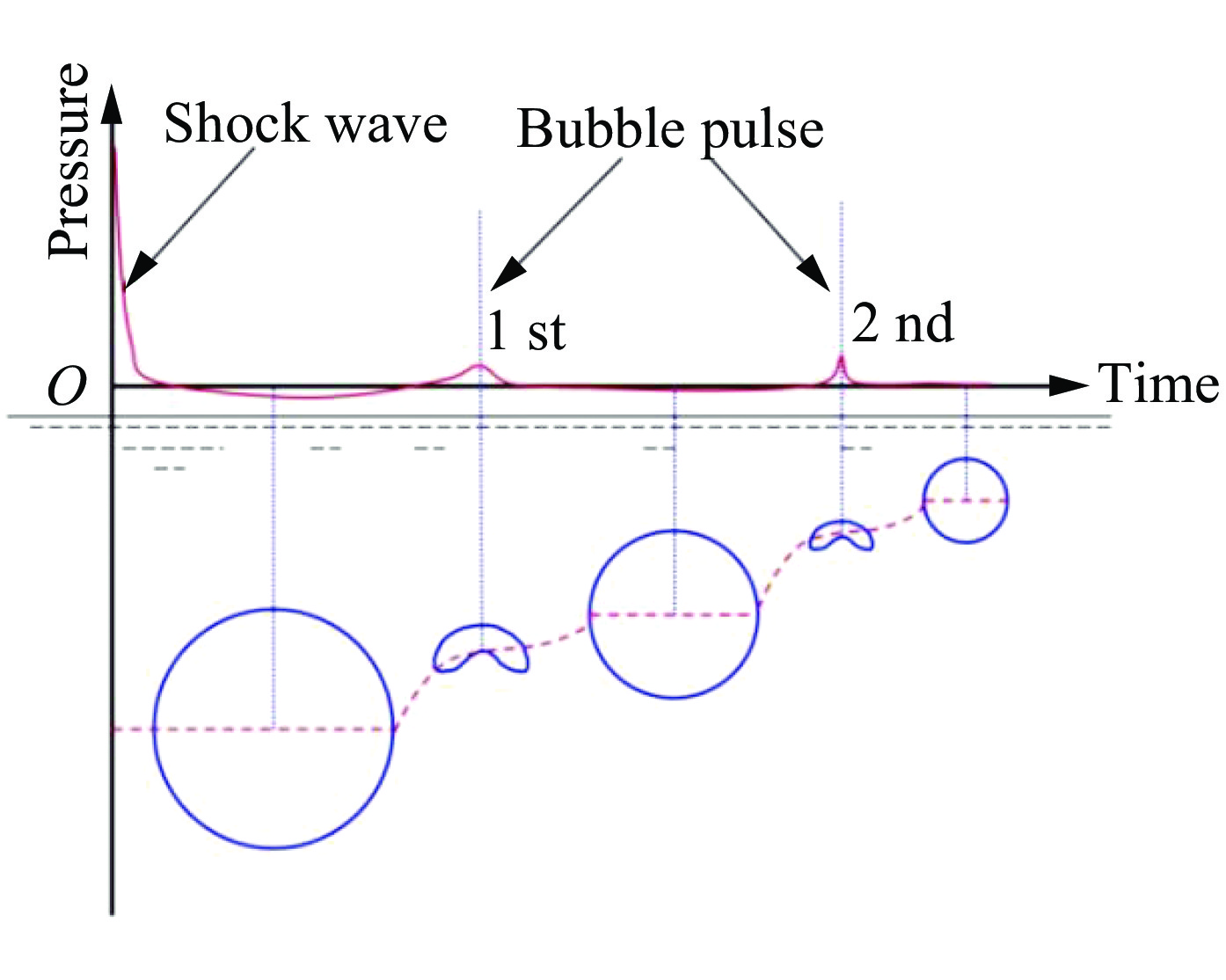
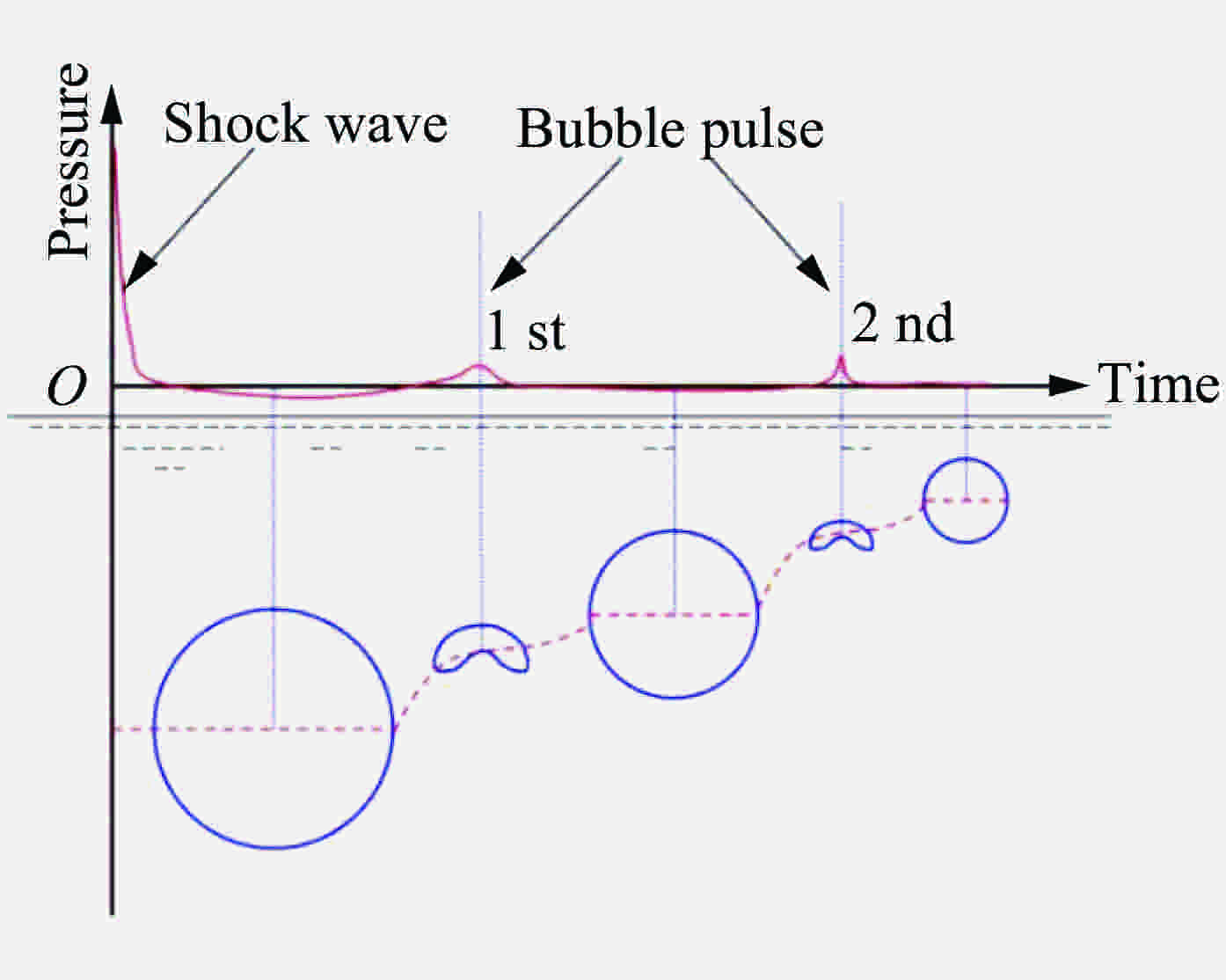
College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, Heilongjiang, China

摘要

摘要: 水下爆炸破冰是复杂的爆破工程，为了研究冰层在水下爆炸冲击波载荷作用下的破碎特性及规律，利用几何动力分析软件LS-DYNA对水下爆炸破冰的过程进行数值模拟，并将计算结果与实验结果进行对比，误差在8%以内，验证了数值模型的有效性。根据本文中的建模方法及建立的模型，计算不同的实验工况：实验场地环境不变，调整爆距分析不同爆距下冰层破碎特性；调整药量、爆距和冰厚，通过正交设计方法设计9组实验方案，应用灰色系统理论对3种因素进行分析，建立了各个因素与破冰半径之间的灰色关联度系数及灰色关联度。分析结果表明：药量为100 g，冰厚为29 cm，水深为2.9 m，爆距范围为0.3～1.5 m破冰的半径范围为0～1.1 m，最佳爆距范围在0.3～0.45 m之间；根据以上9种工况的分析可知，药量(100、200、300 g)、爆距(0.3、0.6、0.9 m)和冰厚(24、28、32 cm)对破冰半径的影响的主次关系依次为爆距、药量、冰厚。
- 水下爆炸 /
- 冲击波载荷 /
- 冰层破碎 /
- 正交试验 /
- 灰色系统理论 /
- 关联度
Abstract: Ice breaking by blasting is a complex process in underwater explosion engineering. In this study we examined the fragmentation characteristics of ice cover with underwater explosion shock wave and simulated the process of underwater explosion breaking ice process using LS-DYNA. We also compared the simulation result with the experimental data and found the min good agreement. Based on this we verified the simulation model and calculated different conditions. Then, keeping the test environment unchanged, we set different detonation distances, and calculated the radius of the ice breaking hole; varying the charge dosage, the detonation distance and the ice thickness, we designed nine group simulation conditions by the orthogonal design method, and analyzed the gray relational degrees and gray incidence coefficients between radius of breaking ice hole and different factors at different levels using the gray system theory. The analytical results showed that, at 100 g of the dosage, the ice thickness is 29 cm, the water depth is 2.9 m, the detonation distance range is 0.3−1.5 m, the radius range of breaking ice hole is 0−1.1 m, and the best detonation distance is between 0.3−0.45 m. According to the analysis of the above nine simulation conditions, the influencing factors that matter most remarkably in underwater ice breaking are the detonation distance (0.3, 0.6, 0.9 m), the dosage (100, 200, 300 g), and the ice thickness (24, 28, 32 cm), in order of their importance.
- underwater explosion /
- shock wave load /
- fragmentation of ice /
- orthogonal experiment /
- gray system theory /
- relational grade

HTML全文

破冰技术的研究是时下研究的热点问题，涉及到江河地区的冰凌灾害，也关系到北极地区的冰区资源争夺，具有重要的经济利益和战略意义。冰凌灾害是我国北方地区面临的主要危害之一，百分之七十的地区都处于寒冷地区，每年都会出现不同程度的冰害^[1]。各国，也越来越重视极地区的战略资源和巨大的经济利益，尤其以破冰为主的破冰船的研究与应用^[2]。虽然已经有相对成熟的破冰技术和尚在研究和关注的破冰技术，而对水下爆炸破冰技术的研究比较稀缺。

目前，破冰的方式有多种，主要有破冰弹破冰、飞机轰炸破冰和大炮轰击破冰以及破冰船破冰等^[3]，本文中关注的是水下爆炸破冰技术的研究。由于水下爆炸作用的巨大威力以及其显著的破冰效果，水下爆炸破冰引起了广泛重视。曲艳东等^[4]、张忠和等^[5]主要对60 cm冰厚、TNT（0～12 kg）大当量条件下水下爆炸破冰的冲击波传播规律以及破冰机理进行了数值模拟研究，得出了药包入水深度直接影响了破冰效果的结论。吴瑞波等^[6]对8、10、12 kg等大当量的水下爆炸破冰进行了实验研究，对药包重量及药包入水深度等参数进行了优化组合研究，得出了最佳组合参数设计。水下爆炸破冰机理的研究通常有理论解析法、实验法和数值模拟方法。由于水下爆炸现象以及冰层本构关系的复杂性，目前理论解析法很难实现水下爆炸破冰的理论解；另外，实验法的昂贵实验费用以及安全性，使得数值模拟研究被广泛使用。数值模拟方法是研究爆炸问题的一种既有效又经济方便的手段，只要方法得当，模拟效果就可以和实际结果一致^[4-5,7]。在我国，水下爆炸破冰的研究对象集中在内河地区的冰层，冰层厚度较厚，厚度为0.5～1 m，炸药的药量范围为8～14 kg，得出了内河冰层区域大当量水下爆炸破冰半径的影响范围。而本文探究对象是沿海地区的冰层区域，冰层厚度较薄，范围在0.2～0.35 m，药量范围为100～300 g的小当量低气泡能炸药水下爆炸冲击波载荷作用下冰层破碎特性，对水下爆炸破冰机理的研究和工程应用具有重要的意义。

水下爆炸冲击波沿着药包的各个方向传播，在冲击波强大的压力作用下，结构容易发生严重的损伤，甚至断裂^[8]。为了研究某个海域冰层厚度为0.29 m小当量普通低气泡能炸药水下爆炸冲击波载荷作用下的冰层破碎特性，本文中使用欧拉–拉格朗日流固耦合算法，对爆破过程进行数值模拟，同时通过实验对模拟结果进行了验证，实验验证与模拟结果取得较好的一致性。

为了进一步研究药量、爆距、冰层厚度对近海海域较薄冰层水下爆炸冲击波载荷破冰的影响，通过正交试验设计不同的实验方案，运用灰色理论对实验方案的模拟结果进行分析，分析结果可为工程爆破以及后续的研究提供参考。

1. 基本理论

1.1 水下爆炸载荷

水下爆炸破冰过程是复杂的冰-水耦合动力学过程，涉及到水下冲击波载荷、气泡脉动载荷、空化效应等对冰结构的影响。水下爆炸的整个物理过程如图1^[9]所示。

图 1 水下爆炸过程

Figure 1. Underwater explosion

下载: 全尺寸图片幻灯片

普通低气泡能炸药水下爆炸产生的载荷主要是冲击波载荷，爆炸之后，冲击波瞬间作用向外传播，爆炸产生的气泡脉动压力峰值不超过冲击波压力的10%～20%，而且气泡脉动的持续时间在秒量级。对于普通的低气泡能炸药水下爆炸，破冰毁伤来源主要是冲击波的毁伤。冲击波在冰盖以下传播路径如图2所示。

图 2 覆冰水下爆炸冲击波路径

Figure 2. Shock wave paths for an underwater explosion with overlying ice

下载: 全尺寸图片幻灯片

1.2 冰体的力学性能

自然结晶形成的冰体有非均匀、各向异性、温度敏感性等特点，在爆炸冲击波等高应变速率载荷作用下呈现为脆断性，爆炸冲击波引起的瞬时压力高达数千兆帕以上，冰壁面受到强烈的压缩而产生粉碎形成破碎区。随着冲击波的传播及衰减，形成应力波，对冰洞的径向产生压应力和压缩变形，对切向形成拉应力和拉伸变形。因此，冰体会产生径向裂纹和环形裂纹，进而形成了裂隙区，如图3所示。

图 3 冰层破碎图

Figure 3. Ice cover fragment

下载: 全尺寸图片幻灯片

冰体材料特性独特，冰层的材料参数分别为^[10]：密度897 kg/m³，剪切模量2.2 GPa，屈服应力2.12 MPa，塑性硬化模量4.26 GPa，体积弹性模量5.26 GPa，塑性失效应变0.35，失效强度−4 MPa。

1.3 欧拉–拉格朗日耦合算法

炸药、水、淤泥、空气采用Euler单元和多物质ALE算法，冰体结构采用Lagrange单元，欧拉单元和拉格朗日单元之间通过耦合定义LS-DYNA中的关键字*CONSTRAINED_LAGANGE_IN_SOLID来实现，其中ALE或Euler部件为主部件，Lagrange为从部件，通过运动约束、罚耦合实现流固耦合^[11]。炸药、水、冰、淤泥、空气的材料本构模型及状态方程见表1。

表 1 数值模拟中的材料模型和状态方程

Table 1. Material models and equation of statefor numerical simulation

材料	本构模型	状态方程
炸药	MAT_HIGH_EXPLOSIVE_BURN	JWL
水	MAT_NULL	Grüneisen
冰	MAT_ISOTROPIC_ELASTIC_FAILURE	无
土壤	MAT_ NULL	LINER_POLYNOMAL
空气	MAT_ NULL	LINER_POLYNOMAL

下载: 导出CSV

| 显示表格

1.4 灰色理论

在系统分析中，常用的定量方法有回归分析、方差分析、主成分分析等数理统计方法，这些方法可以解决许多的实际问题。但是，他们往往要求大量的样本，而且要求有典型的概率分布，在实际情况中很难实现^[12-13]。灰色理论中的灰色关联分析法则不受这些局限，根据因素之间的发展态势的相似或相异程度来衡量因素间的关联程度。这种方法通过一定的数据处理，在随机的因素序列间找到他们的关联性，通过灰色关联度分析确定系统因素间的影响或者因素对系统主行为的贡献度，通过分析灰色关联度发现主要影响因素。灰色理论实用价值很大^[14]，其分析步骤为：

(1)设计模拟方案，确定影响因素和考核指标，影响因素序列即为比较列，考核指标即为参考列；

(2)无量纲化，即将比较数列和参考数列进行无量纲化处理；

(3)计算关联度系数，即经过数据变换分析关联度；

(4)对关联度进行分析。

1.4.1 无量纲化

在进行灰色系统理论优化时，由于因素序列具有不同的量纲与范围，在计算灰色关联度之前需要对数据列进行无量纲化处理，处理方法如下：

${x_i}(k) = \frac{{x_i^{(0)}(k) - \min x_i^{(0)}(k)}}{{\max x_i^{(0)}(x) - \min x_i^{(0)}(x)}}$

(1)

式中：i=1，···，m；k=1，···，n；m和n分别为实验次数和目标次数；x_i⁽⁰⁾(k)为原序列；x_i(k)为处理后序列；min x_i⁽⁰⁾(k)为原始序列最小值；max x_i⁽⁰⁾(k)为原始序列最大值。

1.4.2 灰色关联度计算

设参考序列为X₀={x₀(k), k=1, 2, ···, n}，比较序列为X_i={x_i(k), k=1, 2, ···, m}，则X_i对于X₀在第k点的灰色关联度系数为：

${\varepsilon _i}\left( k \right) = \frac{{{\varDelta _{\min }} + \xi {\varDelta _{\max }}}}{{{\varDelta _{0i}}\left( k \right) + \xi {\varDelta _{\max }}}}$

(2)

式中：Δ_0i(k)为比较序列与参考序列在k点的差值。

$\begin{array}{l} {\varDelta _{\min }} = \mathop {\min }\limits_i \mathop {\min }\limits_k \left| {{x_0}\!\left( k \right) - {x_i}\!\left( k \right)} \right|\\ {\varDelta _{\max }} = \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{x_0}\!\left( k \right) - {x_i}\!\left( k \right)} \right| \end{array}$

(3)

ξ为分辨率系数，分辨率ξ取值原则^[15]需要体现关联度整体性和抗干扰性，按下式取值参考：

$\varDelta = \frac{1}{{mn}}\sum\limits_{i = 1}^m {\sum\limits_{k = 1}^n {\left| {{x_0}(k) - {x_i}(k)} \right|} }$

(4)

记ε_Δ=Δ/Δ_max，取值为ε_Δ≤ξ≤2ε_Δ；当Δ_max＞3Δ时，ε_Δ≤ξ≤1；当Δ_max≤3Δ时，1.5ε_Δ≤ξ≤2ε_Δ。比较序列X_i对于参考序列X₀的关联度为：

${\gamma _{0i}} = \frac{1}{n}\sum\limits_{k = 1}^n {{\varepsilon _{0i}}(k)}$

(5)

比较关联度大小，γ_0i越大，关联度越高。

2. 现场实验

现场实验条件为冬季某海域，冰层厚度为0.29 m，区域没有裂缝的完整冰层，炸药为普通低气泡能炸药，药量为100 g，水深条件为2.9 m，爆距为0.32 m。进行了冰下水下固定爆炸，选好实验爆点，通过人工钻孔，将药包放在冰面爆点正下方，在远离爆源的地方安装起爆装置。实验现场如图4所示。

图 4 实验爆破前

Figure 4. Experiment sife

下载: 全尺寸图片幻灯片

冰洞破口半径为R=0.8 m。

3. 数值模型建立及有效性验证

3.1 有限元建模

根据现场实验条件和研究问题的对称性，建立数值模拟模型，设置欧拉-拉格朗日流固耦合作用。计算模型的外表面均为无限区域，建立无反射边界条件，药包为球形装药，起爆为中心点起爆。模型尺寸为1 000 cm×1 000 cm×519 cm，采用1/4对称模型。

3.2 有效性验证

选取不同时刻水下爆炸破冰的压力云图和冰层破坏云图，如图5所示。

图 5 冰层水压力云图

Figure 5. Water pressure contour of ice cover

下载: 全尺寸图片幻灯片

由数值模拟结果（见图6）可知，冰洞的半径为R=0.802 m，实验结果冰洞半径为R=0.87 m，误差为7.81%，模拟结果与实验结果误差较小。由图5可以看出：炸药在零速度的水介质中产生初始冲击波，并形成明显的波阵面向四周传播；当t=600 μs时，冰层开始受到冲击波的压力作用，在冰层表面产生应力；当t=1 400 μs时，冰层受到的压力达到了冰层的破坏极限，冰面产生环形裂纹和径向裂纹；当t=3 000 μs时，随着冲击波的传播以及泥土层反射的冲击波继续作用在冰面上，冰层表面的破口继续扩大，继续引起裂纹的发育和震动，破冰的程度增大；当t=4 300 μs时，冰层的破口不再继续增大，裂隙区也不再继续扩展，冰层的破坏已经达到了稳定。图6中冰层破坏情况与图3中冰层破坏机理图一致，包含冰层的破碎区和裂隙区，同时还有扩展的裂纹。从模拟结果可以看出，本文的有限元模型能够很好地预测小当量炸药水下爆炸冲击波作用下的冰洞破碎半径。

图 6 冰层破坏图

Figure 6. Ice cover fragment

下载: 全尺寸图片幻灯片

4. 数值模拟结果分析

4.1 爆距对冰层破碎的影响

为了探究在现场药量100 g、水深2.9 m、冰厚0.29 m的实验环境下爆距对破冰的影响，设置爆距为0.3、0.6、0.9、1.2、1.5 m，对这5种工况进行数值模拟研究。模拟结果如图7所示。

图 7 爆距对破冰的影响

Figure 7. Diameter of ice breaking holdversus denonation distance

下载: 全尺寸图片幻灯片

由图7可以看出，药量100 g、爆距1.2 m以内爆炸可以产生冰洞，而且随着爆距的变化冰层破洞半径也会不同，爆距越近或者越远都有可能达不到最佳的破冰效果。药量100 g的最佳爆距为0.3～0.45 m；当爆距超过1.2 m时，药量100 g不能对0.29 m冰层造成冰洞破损。

4.2 药量、爆距和冰厚对冰层破碎的影响

应用灰色理论分析药量、爆距和冰厚对冰层破碎的影响。采用正交试验设计9种模拟工况，主要研究药量、爆距和冰厚对水下爆炸冲击波破冰的毁伤影响，对水下爆炸破冰参数进行优化设计。由文献[6-7]可知，影响水下爆炸冲击波对冰层的破坏损伤主要影响因素为药量、装药位置以及冰厚，分别记为X₁、X₂、X₃，水平数均取3，具体试验条件见表2～3。

表 2 正交试验因素水平

Table 2. Factor level of orthogonal experiment

水平	X₁/g	X₂/m	X₃/m
1	100	0.3	0.24
2	200	0.6	0.28
3	300	0.9	0.32

下载: 导出CSV

| 显示表格

表 3 正交试验设计方案

Table 3. Factor level of orthogonal experiment

工况	X₁/g	X₂/m	X₃/m
1	100	0.3	0.24
2	100	0.6	0.28
3	100	0.9	0.32
4	200	0.3	0.32
5	200	0.6	0.24
6	200	0.9	0.28
7	300	0.3	0.28
8	300	0.6	0.32
9	300	0.9	0.24

下载: 导出CSV

| 显示表格

将爆破后冰层破洞半径作为参考数列，记为y₁(k)；将药量、爆距和冰厚取为比较数列，记为x₁(k)、x₂(k)、x₃(k)。则比较数列与参考数列的表达式为：

$\quad\quad\quad{X_i} = ({x_i}(1),{x_i}(2), \cdot \cdot \cdot ,{x_i}(k))\;\;\;\;\;i = 1,2,3\quad\quad\quad(6)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \;\;\;\;\;$

$\quad\quad\quad Y = (y(1),y(2), \cdot \cdot \cdot ,y(k))\quad\quad\quad\quad(7)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\;\;$

对以上9种模拟方案进行数值模拟，得出模拟结果序列值为： $y^{(0)}_{9}$ =(0.300, 0.701, 0.602, 0.400, 1.100，0.400, 0.299, 0.199, 0.801)。

为了保证计算关联度的准确性，将数据列进行无量纲化，无量纲化后得到的结果见表4。

表 4 正交试验各序列区域值

Table 4. Sequences region value of orthogonal experiment

工况	x₁	x₂	x₃	y
1	0	0	0	0.112
2	0	0.5	0.5	0.557
3	0	1.0	1.0	0.447
4	0.5	0	1.0	0.223
5	0.5	0.5	0	1.000
6	0.5	1.0	0.5	0.223
7	1.0	0	0.5	0.111
8	1.0	0.5	1.0	0
9	1.0	1.0	0	0.668

下载: 导出CSV

| 显示表格

对于破冰半径，由式(4)有：

$\varDelta = \frac{1}{{mn}}\sum\limits_{i = 1}^m {\sum\limits_{k = 1}^n {\left| {{x_0}(k) - {x_i}(k)} \right|} } = 0.459$

(8)

由于ε_Δ=Δ/Δ_max=0.459/1=0.459，且Δ_max＜3Δ，因此1.5ε_Δ≤ξ≤2ε_Δ，取ξ=0.8。根据式(2)～(5)、式(8)，计算因子对试验指标的关联系数和关联度见表5。

表 5 不同因素在不同水平下对破冰半径的关联度系数及关联度

Table 5. Gray relational degrees and gray incidence coefficients between radius ofbreaking ice breaking hole and different factors at different levels

工况	关联度系数
工况	药量X₁	爆距X₂	冰厚X₃
1	0.940	0.970	0.940
2	0.632	1.000	1.000
3	0.687	0.633	0.633
4	0.796	0.834	0.543
5	0.659	0.659	0.476
6	0.796	0.543	0.796
7	0.507	0.94	0.721
8	0.476	0.659	0.476
9	0.757	0.757	0.584
关联度	0.694	0.774	0.685

下载: 导出CSV

| 显示表格

由表5可知，按关联度从大到小的顺序是，爆距、药量和冰厚。

5. 结　论

水下爆炸破冰是预防冰凌灾害以及实施水下战略武器发射的有效措施。本文的主要结论如下。

（1）利用欧拉-拉格朗日耦合方法进行水下爆炸破冰模拟，模拟结果与实验结果吻合良好，误差在8%以内，可以很好地进行低气泡能炸药水下爆炸破冰的研究。

（2）冰层为0.29 m、药量为100 g、爆距为0.2～1.5 m时，水下爆炸冰层破坏半径范围为0～1.1 m。此外，爆距超过1.2 m时，冲击波载荷不会对冰层造成破坏。爆距对冰层破坏半径的影响较大，最佳爆距为0.3～0.45 m。

（3）计算冰层厚度24～32 cm、药量100～300 g不同爆距条件下的破冰半径，将正交试验法和灰色关联度分析法有效结合，计算了药量、爆距、冰厚不同因素与破冰半径的关联度系数及关联度，得出了3种因素的影响关系。这为水下爆炸破冰参数优化提供了有效的研究思路，也拓展了灰色理论的应用领域。

图 1 水下爆炸过程

Figure 1. Underwater explosion

下载: 全尺寸图片幻灯片

图 2 覆冰水下爆炸冲击波路径

Figure 2. Shock wave paths for an underwater explosion with overlying ice

下载: 全尺寸图片幻灯片

图 3 冰层破碎图

Figure 3. Ice cover fragment

下载: 全尺寸图片幻灯片

图 4 实验爆破前

Figure 4. Experiment sife

下载: 全尺寸图片幻灯片

图 5 冰层水压力云图

Figure 5. Water pressure contour of ice cover

下载: 全尺寸图片幻灯片

图 6 冰层破坏图

Figure 6. Ice cover fragment

下载: 全尺寸图片幻灯片

图 7 爆距对破冰的影响

Figure 7. Diameter of ice breaking holdversus denonation distance

下载: 全尺寸图片幻灯片

表 1 数值模拟中的材料模型和状态方程

Table 1. Material models and equation of statefor numerical simulation

材料	本构模型	状态方程
炸药	MAT_HIGH_EXPLOSIVE_BURN	JWL
水	MAT_NULL	Grüneisen
冰	MAT_ISOTROPIC_ELASTIC_FAILURE	无
土壤	MAT_ NULL	LINER_POLYNOMAL
空气	MAT_ NULL	LINER_POLYNOMAL

下载: 导出CSV

表 2 正交试验因素水平

Table 2. Factor level of orthogonal experiment

水平	X₁/g	X₂/m	X₃/m
1	100	0.3	0.24
2	200	0.6	0.28
3	300	0.9	0.32

下载: 导出CSV

表 3 正交试验设计方案

Table 3. Factor level of orthogonal experiment

工况	X₁/g	X₂/m	X₃/m
1	100	0.3	0.24
2	100	0.6	0.28
3	100	0.9	0.32
4	200	0.3	0.32
5	200	0.6	0.24
6	200	0.9	0.28
7	300	0.3	0.28
8	300	0.6	0.32
9	300	0.9	0.24

下载: 导出CSV

表 4 正交试验各序列区域值

Table 4. Sequences region value of orthogonal experiment

工况	x₁	x₂	x₃	y
1	0	0	0	0.112
2	0	0.5	0.5	0.557
3	0	1.0	1.0	0.447
4	0.5	0	1.0	0.223
5	0.5	0.5	0	1.000
6	0.5	1.0	0.5	0.223
7	1.0	0	0.5	0.111
8	1.0	0.5	1.0	0
9	1.0	1.0	0	0.668

下载: 导出CSV

表 5 不同因素在不同水平下对破冰半径的关联度系数及关联度

Table 5. Gray relational degrees and gray incidence coefficients between radius ofbreaking ice breaking hole and different factors at different levels

工况	关联度系数
工况	药量X₁	爆距X₂	冰厚X₃
1	0.940	0.970	0.940
2	0.632	1.000	1.000
3	0.687	0.633	0.633
4	0.796	0.834	0.543
5	0.659	0.659	0.476
6	0.796	0.543	0.796
7	0.507	0.94	0.721
8	0.476	0.659	0.476
9	0.757	0.757	0.584
关联度	0.694	0.774	0.685

下载: 导出CSV

参考文献(15)

[1]	夏长富. 水下人工爆破冰凌技术研究与实践 [J]. 爆破, 2014, 31(2): 126–129. DOI: 10.3963/j.issn.1001-487X.2014.02.028. XIA Changfu. Research and practice of underwater ice jam breaking by manual-operated blasting [J]. Blasting, 2014, 31(2): 126–129. DOI: 10.3963/j.issn.1001-487X.2014.02.028.
[2]	张雨, 李岳阳, 王敏. 极地破冰船发展现状与趋势 [J]. 舰船科学与技术, 2017, 39(12): 188–193. DOI: 10.3404/j.issn1672-7649. 2017.12.040. ZHANG Yu, LI Yueyang, WANG Min. Overview and trend of the icebreakers [J]. Ship and Technology, 2017, 39(12): 188–193. DOI: 10.3404/j.issn1672-7649. 2017.12.040.
[3]	解文辉, 何秉顺, 李华新. 黄河防凌爆炸破冰效果 [J]. 工程爆破, 2014, 20(6): 29–31. DOI: 10.3969/j.issn.1006-7051.2014.06.007. XIE Wenhui, HE Bingshun, LI Huaxin. The effect of ice breaking by explosion for the yellow river ice flood prevention [J]. Engineering Blasting, 2014, 20(6): 29–31. DOI: 10.3969/j.issn.1006-7051.2014.06.007.
[4]	曲艳东, 刘万里, 翟诚. 水下爆炸冲击波传播规律数值分析 [J]. 爆破, 2017, 34(2): 100–104. DOI: 10.3963/j.issn.1001-487X.2017.02.019. QU Yandong, LIU Wanli, ZHAI Cheng. Numerical simulation of propagation law of shock waves in process of breaking ice by underwater blasting [J]. Blasting, 2017, 34(2): 100–104. DOI: 10.3963/j.issn.1001-487X.2017.02.019.
[5]	张忠和, 梁向前, 王树理. 水下爆破破冰机理的数值分析研究 [J]. 爆破, 2015, 32(6): 150–155. DOI: 10.3963/j.issn.1001-487X.2015.03.027. ZHANG Zhonghe, LIANG Xiangqian, WANG Shuli. Numerical simulation of ice breaking mechanism of underwater blasting [J]. Blasting, 2015, 32(6): 150–155. DOI: 10.3963/j.issn.1001-487X.2015.03.027.
[6]	吴瑞波, 郝明盛, 武彩岗, 等. 水中爆破破冰参数的优化实验 [J]. 工程爆破, 2014, 20(6): 25–28. DOI: 10.3969/j.issn.1006-7051.2014.06.006. WU Ruibo, HAO Mingsheng, WU Caigang, et al. The parameters optimization experiment of ice breaking by underwater blasting [J]. Engineering blasting, 2014, 20(6): 25–28. DOI: 10.3969/j.issn.1006-7051.2014.06.006.
[7]	钟冬望, 黄小武, 殷秀红, 等. 水下爆炸冲击波的数值模拟与实验研究 [J]. 爆破, 2015, 32(4): 14–18. DOI: 10.3963/j.issn.1001-487X.2015.04.004. ZHONG Dongwang, HUANG Xiaowu, YIN Xiuhong, et al. Numerical simulation and experimental study of underwater explosion shock wave [J]. Blasting, 2015, 32(4): 14–18. DOI: 10.3963/j.issn.1001-487X.2015.04.004.
[8]	姚熊亮, 汪玉, 张阿漫. 水下爆炸气泡动力学[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012: 1−3.
[9]	宗智, 赵延杰, 邹丽. 水下爆炸结构毁伤的数值计算[M]. 北京:科学出版社, 2014: 3−7.
[10]	郭军伟. 冰体力学性质及其受到爆炸与冲击波作用研究[D]. 郑州: 华北水利水电大学, 2014: 34−37.
[11]	康德, 严平. 基于LS-DYNA的高速破片水中运动特性流固耦合数值模拟 [J]. 爆炸与冲击, 2014, 34(5): 534–538. DOI: 10.11883/1001-1455(2014)05-0534-05. KANG De, YAN Ping. Movement characteristics of high-velocity fragments in water medium: numerical simulation using LS-DYNA [J]. Explosion and Shock Waves, 2014, 34(5): 534–538. DOI: 10.11883/1001-1455(2014)05-0534-05.
[12]	顾强, 张世豪, 安晓红, 等. 基于灰色理论的两点爆炸起爆参数优化设计 [J]. 爆炸与冲击, 2015, 35(3): 359–365. DOI: 10.11883/1001-1455(2015)03-0359-07. GU Qiang, ZHANG Shihao, AN Xiaohong, et al. Optimization design for priming parameters of two-point explosion based on gray theory [J]. Explosion and Shock Waves, 2015, 35(3): 359–365. DOI: 10.11883/1001-1455(2015)03-0359-07.
[13]	林加剑, 任辉启, 沈兆武. 应用灰色系统理论研究爆炸成形弹丸速度的影响因素 [J]. 弹箭与制导学报, 2009, 29(3): 112–116. DOI: 10.3969/j.issn.1673-9728.2009.03.033. LIN Jiajian, REN Huiqi, SHEN Zhaowu. Study on primary influence factors for application of gray system theory to velocity of explosive forming projectile [J]. Journal of Projectiles Rockets Missiles and Guidance, 2009, 29(3): 112–116. DOI: 10.3969/j.issn.1673-9728.2009.03.033.
[14]	傅立. 灰色系统理论及其应用[M]. 北京: 科学技术文献出版社, 1992: 1−20.
[15]	吕锋. 灰色系统关联度之分辨率系数的研究 [J]. 系统工程理论与实践, 1997, 17(6): 49–54. DOI: 10.3321/j.issn:1000-6788.1997.06.011. LYU Feng. Research on the identification coefficient of relational grade for grey system [J]. Systems Engineering Theory and Practice, 1997, 17(6): 49–54. DOI: 10.3321/j.issn:1000-6788.1997.06.011.

施引文献

期刊类型引用(7)

1.	时本军，李杰，徐小辉，徐天涵，郭纬，李孝臣，李超，李干. 混凝土中多点聚集爆炸效应起爆参数优化设计. 爆炸与冲击. 2025(01): 153-167 . 本站查看
2.	蒲文龙，申罗飞，刘洋. 基于ANSYS/LS-DYNA的防凌减灾微差爆破数值模拟. 黑龙江科技大学学报. 2023(03): 325-332 . 百度学术
3.	王莹，秦业志，王志凯，姚熊亮. 不同类型炸药水下爆炸时冰层损伤特性研究. 振动与冲击. 2022(09): 189-198 . 百度学术
4.	王燕，李梦群，杨淼慧，徐锦，王佳奇. 复合防护结构抗破片侵彻性能的研究. 火工品. 2022(04): 16-20 . 百度学术
5.	吴榕榕，王健，王英霖. 弹体高速侵彻冰体研究. 弹箭与制导学报. 2022(04): 74-80 . 百度学术
6.	王英霖，王健，诸庆生. 高速弹体侵彻冰材料过程数值模拟研究. 兵器装备工程学报. 2021(04): 62-67 . 百度学术
7.	陈德勇，贺小轩，杨慧，相光友，左祖雄. 瓦斯爆炸冲击波对通风设施破坏情况数值模拟影响因素分析. 安全. 2021(12): 36-42 . 百度学术